简支箱梁振动噪声影响参数研究

林玉森，田 伦，尹 昊，刘宗礼

(1.石家庄铁道大学 土木工程学院，河北 石家庄 050043； 2.石家庄铁道大学 道路与铁道工程安全保障省部共建教育部重点实验室，河北 石家庄 050043)

随着我国高速铁路建设规模的不断扩大，桥梁结构噪声问题必须引起重视。列车通过桥梁时引起桥梁的振动进而产生结构噪声。结构噪声的频率主要集中在200 Hz以下，具有较强的穿透能力，传播距离远，长期处于低频噪声空间内会对人体健康产生严重危害。研究低频结构噪声的产生原理和减振降噪技术具有重要的工程价值。

李克冰[1]将全过程迭代法用于分析车桥耦合振动，通过基于Helmholtz方程的边界元法求得32 m混凝土槽型梁的结构噪声分布规律。宋晓东[2]使用2.5维声学有限元/无限元法得出声屏障能显著降低钢轨振动辐射噪声，高弹性扣件能降低桥梁结构噪声。张小安[3]使用基于显式隐式混合积分法进行车线桥耦合振动分析，求解了高速铁路32 m混凝土箱梁的结构噪声，与李小珍等[4]的现场测试结果对比后，验证了其数值模型的合理性。李晶[5]将有限元算法与边界元算法相结合，发现增大桥梁的阻尼比能降低噪声的辐射声压级。王一干[6]对一座设有声屏障的30 m双线混凝土简支梁进行了结构噪声测试，发现声屏障对200 Hz以下的噪声降噪效果较差。宋立忠[7]实测了城市轨道交通30 m混凝土简支箱梁在70 km/h的列车荷载作用下的结构噪声分布情况。雷晓燕等[8]通过声学实验，验证了32 m混凝土简支箱梁缩尺模型和原型在动力响应与噪声辐射特性上的相似性。刘林芽等[9]采用了有限元法和快速多极边界元法联合仿真的方式，对32 m双线简支箱梁结构噪声的空间分布特性进行分析。尹镪等[10]采用软件TTBSIM和Sysnoise联合仿真模拟了32 m简支梁噪声辐射的时域结果，分析了列车车速为200 km/h时，该桥噪声辐射随时间变化的规律。崔喆[11]提出了一种基于最小二乘法的噪声辐射稳定算法。丁桂保等[12]依据箱梁结构位移与声压的表达式，预测了48 m的钢桁梁桥在250 km/h的高速列车荷载作用下的低频噪声辐射特性。谢伟平、孙亮明等[13-14]提出了一种求解混凝土箱梁声辐射特性的半解析方法，能够得到桥梁截面二维声场内任意点的声压大小。

本文以32 m简支箱梁为研究对象，建立了高速铁路简支箱梁结构噪声预测模型，并采用Kik-piotrowski轮轨接触算法，提高了轮轨力计算结果的精确性，获得了更准确的结构噪声计算结果。通过基于Helmholz方程的边界元法，分析了简支箱梁的结构噪声声压级的频域分布特性和空间分布特性，探究了车速及构件厚度等因素对桥梁结构噪声的影响规律，对高速铁路简支桥梁的减振降噪措施起到一定的参考作用。

1 振动噪声模型

1.1 车桥耦合模型

车桥耦合模型由车辆模型、轨道模型和桥梁模型组成，三个系统之间通过轮轨接触关系和边界处的变形协调关系进行耦合，形成了大耦合振动模型。机车车辆由车体、转向架和轮对构成，轨道模型采用柔性轨道，充分考虑车辆荷载作用下钢轨的振动情况。钢轨通过粘弹性力元与刚性半轨枕进行连接，轨枕仅考虑垂向和横向平动以及绕纵轴的转动。桥梁模型采用实体单元模型。整个大耦合系统的运动方程[15]为

(1)

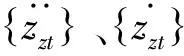
1.2 Helmholtz方程边界元求解

线性声学Helmholtz方程表达式为

2p+k2p=0

(2)

振动结构外声场辐射问题应符合诺依曼边界条件以及萨默菲尔德辐射条件，即

(3)

(4)

使用加权余量法进行方程(2)的求解，并代入Helmholtz方程的单位点源奇异解G(I,J)表达式，即可得到空间内任意点J的法向振速表达式：

G(I,J)=e-jkr/4πr

(5)

(6)

在求解域内进行积分，可得

(7)

公式(7)即为基于Helmholtz方程的边界积分公式，可以计算得到声场内任意点的声压。

2 车桥耦合动力响应分析

2.1 工程概况

列车模型选取CRH3型列车，编组形式为8节列车形式，以250 km/h匀速通过32 m简支箱梁桥。轨道结构采用柔性轨道，轨道不平顺采用CRH2017。32 m双线混凝土简支箱梁长32.6 m，计算跨径31.5 m，梁高3.05 m，顶板宽13.4 m，底板宽5.5 m；顶板、底板和腹板的厚度分别为0.3、0.28和0.45 m。图1为车辆模型和桥梁模型图。

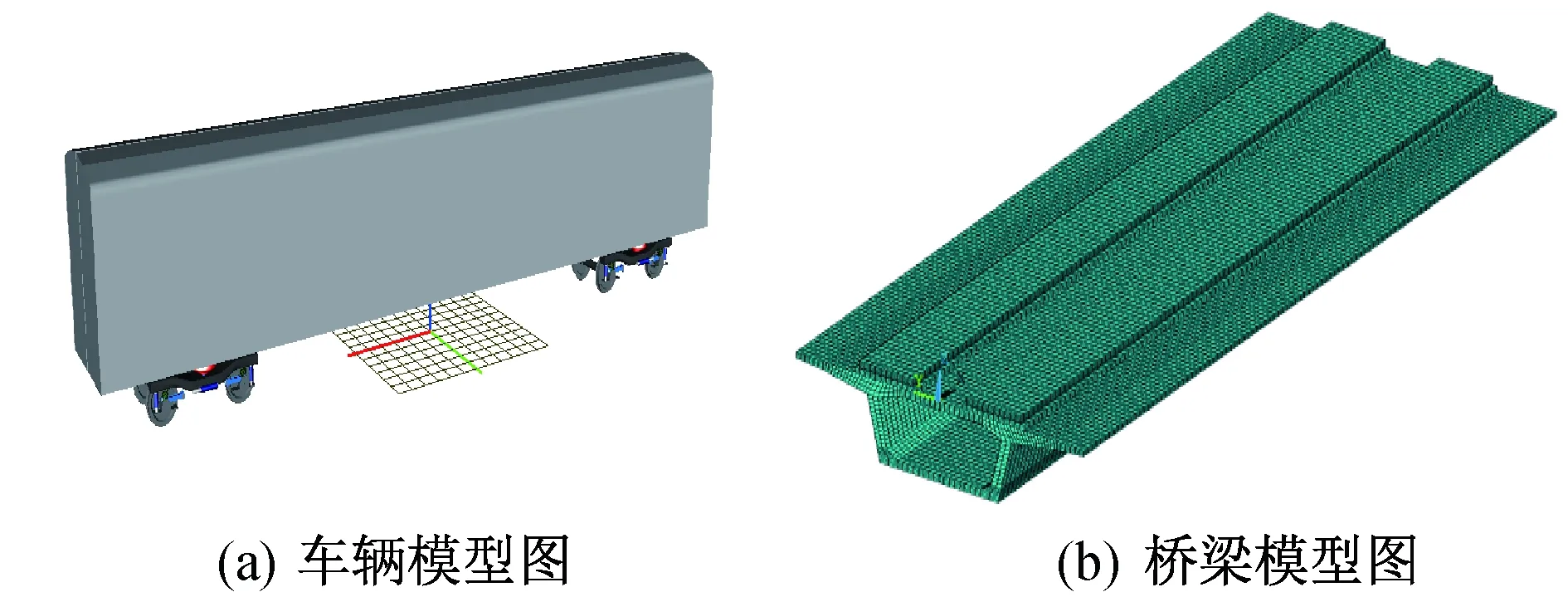
图1 车辆模型和桥梁模型图Fig.1 Vehicle model and bridge model diagram

2.2 桥梁动力响应

图2列出列车以250 km/h通过简支梁时梁体的竖向加速度曲线和竖向加速度频谱曲线图。桥梁竖向加速度的振动频率主要分布在25 Hz附近，在6、20、31.5 Hz附近处存在峰值。

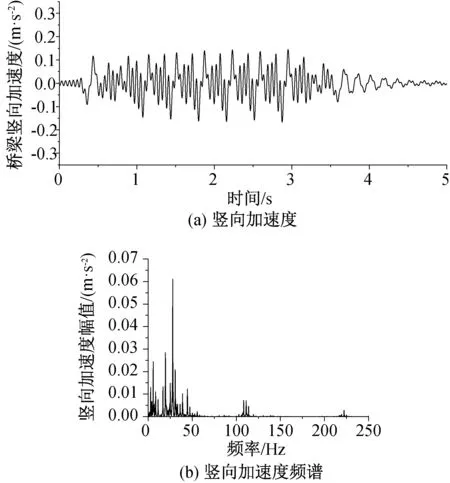
图2 跨中振动加速度曲线Fig.2 Mid-span vibration acceleration curve

3 桥梁结构噪声分析

在VA-One声学仿真软件中建立桥梁结构的有限元模型和道床结构的统计能量模型，采用板单元模拟道床结构和32 m简支梁桥。对箱梁的构件进行简化处理，翼板和顶板厚0.3 m，腹板厚0.45 m，底板厚0.28 m。对板单元进行单元网格划分，每个单元的最大边长为0.25 m。底座板和轨道板采用SEA板单元进行模拟，底座板厚度0.184 m，轨道板厚0.2 m。将垂向轮轨力的1/3倍频程波形施加在桥梁跨中SEA轨道板的最不利位置上，采用边界元方法[16]求解空间内的桥梁结构噪声辐射特性。

3.1 场点声压级

为研究列车高速运行下简支箱梁所产生结构噪声的声压级随距离改变的分布状况，在桥跨跨中截面内选取16个场点作为研究对象。场点P1—P3位于顶板跨中截面正上方，与顶板竖向间距分别为5、3、1 m；场点P4—P7位于底板跨中截面正下方，与底板竖向间距分别为1、3、5、7 m；场点P8—P12位于简支梁跨中正下方10 m处的一侧，各点横向距离间隔5 m；场点P13—P16分别位于距离简支梁跨中中心线25 m处，竖向距离间隔3 m，场点分布如图3所示。

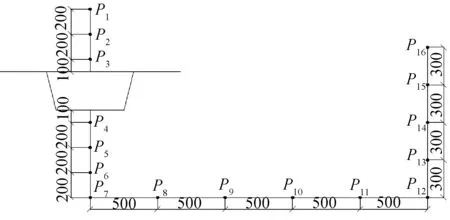
图3 声压场点布置图(单位：cm)Fig.3 Sound pressure field point layout diagram

表1为各场点总声压级，场点P3的噪声总声压级最大，为117.42 dB。对比表1中各场点的声压值，再结合图4以得出在频率小于80 Hz时，竖直方向上场点离梁体越近，测得的噪声声压级越大，声压级增加的幅度越大。对于距离底板和顶板相同的场点，顶板测出的噪声声压级大于底板测出的噪声声压级。这可能是由于振动能先传递到顶板后传递到底板，顶板获得的振动能大于底板获得的振动能，所以顶板的噪声辐射能力强于底板。噪声声压级在底板下的变化范围小于顶板上的变化范围。

表1 场点总声压级

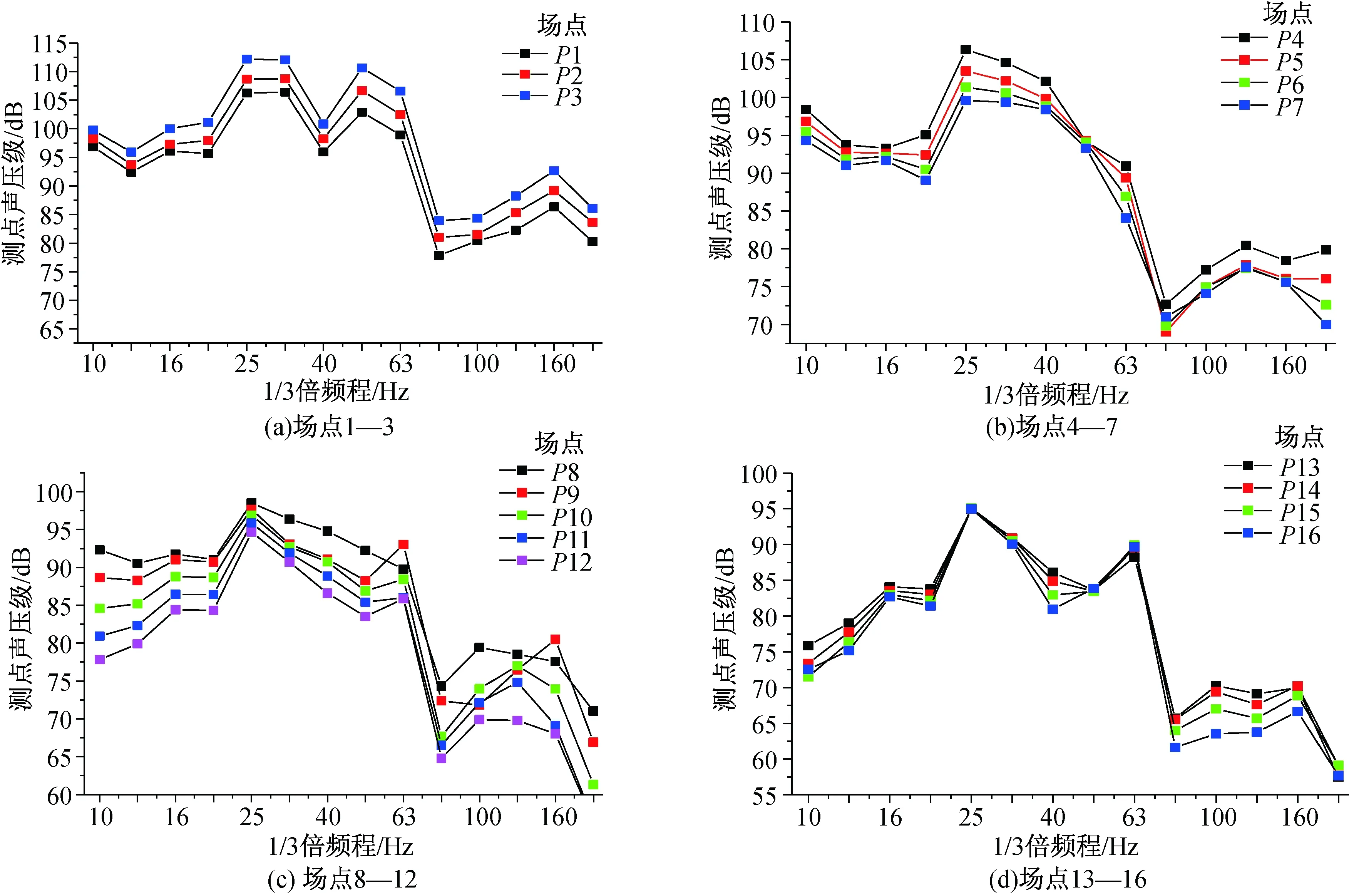
图4 线性声压级曲线图Fig.4 Linear sound pressure level graph

3.2 跨中噪声空间分布规律

为了研究桥梁结构周围的噪声声压级空间分布情况，选取整个声场作为研究对象。桥梁在12.5、25、63、80、125、200 Hz中心频率点下的1/3倍频程二维声场声压级分布云图，如图5所示。

由图5可知，(1)桥梁结构噪声辐射区域主要集中在顶板正上方和底板正下方，顶板上方的声压级强度大于底板下方的声压级强度。桥梁结构竖向的声压级强度大于横向的声压级强度。(2)在f=63 Hz时，噪声的辐射范围最广，噪声的分布比较复杂，具有明显的单一指向性，存在多个峰值区域，且噪声声压级在横向衰减最慢。(3)箱梁的腹板和底板对噪声的传播有遮蔽作用。顶板振动向外传播的噪声能量一部分被腹板和底板吸收，一部分在空腔内经多次反射而逐渐消退，在箱梁内外出现差值。(4)低频声场分布规则，指向性单一。高频声场分布分散，指向性复杂。

4 噪声影响因素研究

P8点位于简支梁跨中正下方10 m处的一侧，能够代表桥梁线路近侧行人所接收到的结构噪声声压级大小，P12点纵向距离简支梁跨中正下方10 m，横向距离简支梁跨中中心线25 m处，能够代表桥梁线路远侧居民区的居民所接收到的结构噪声声压级大小。本文着重研究行车速度、板厚和腔室结构变化对这两个场点噪声声压级的影响。

4.1 速度对噪声影响

行车速度的变化间接影响了桥梁振动响应的结果，继而影响桥梁结构辐射声场的声压大小和分布。本节以20 km/h的速度为间隔，研究列车290～350 km/h时速下的结构振动声辐射。

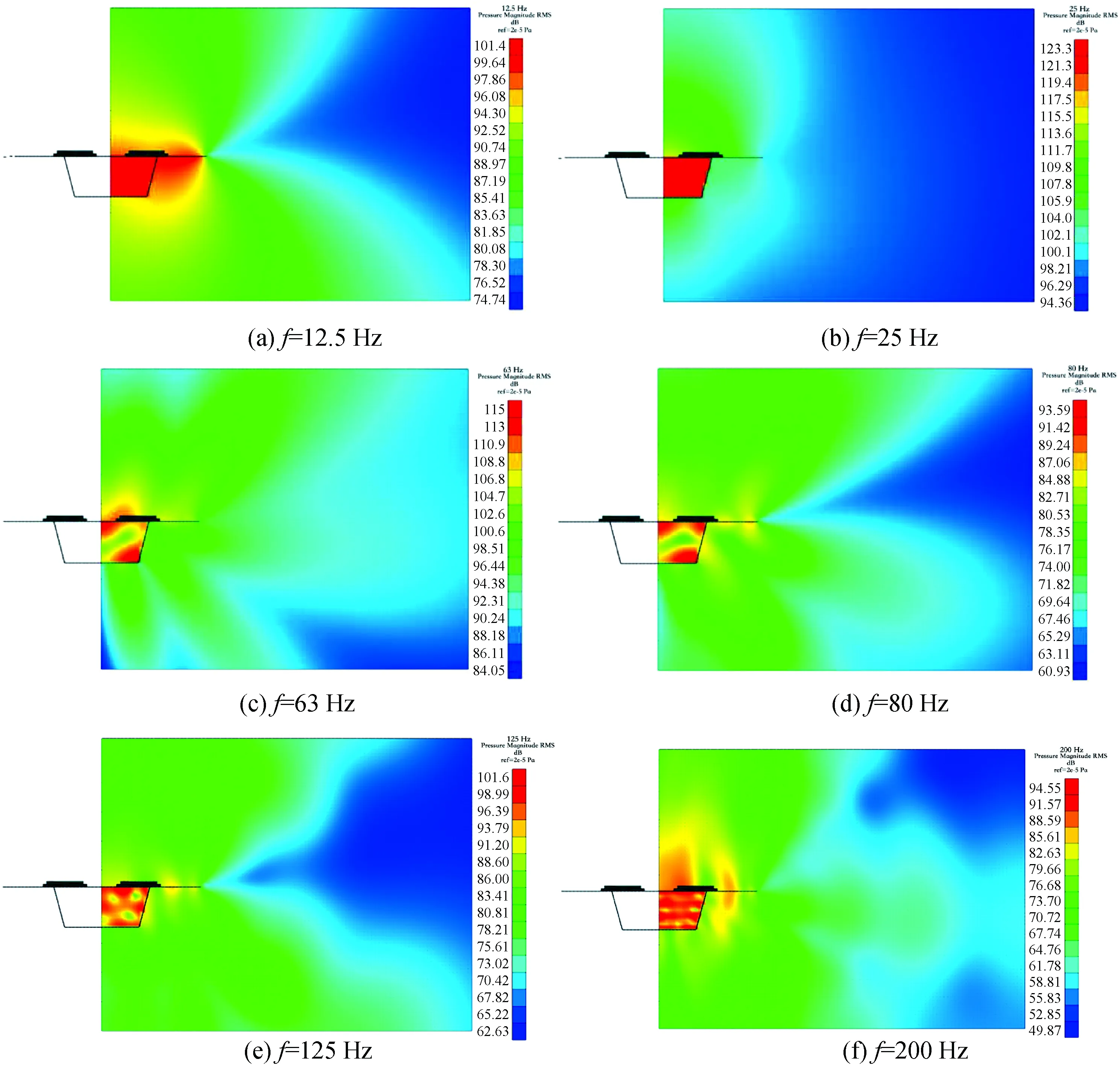
图5 声压级分布云图Fig.5 Sound pressure level distribution cloud chart

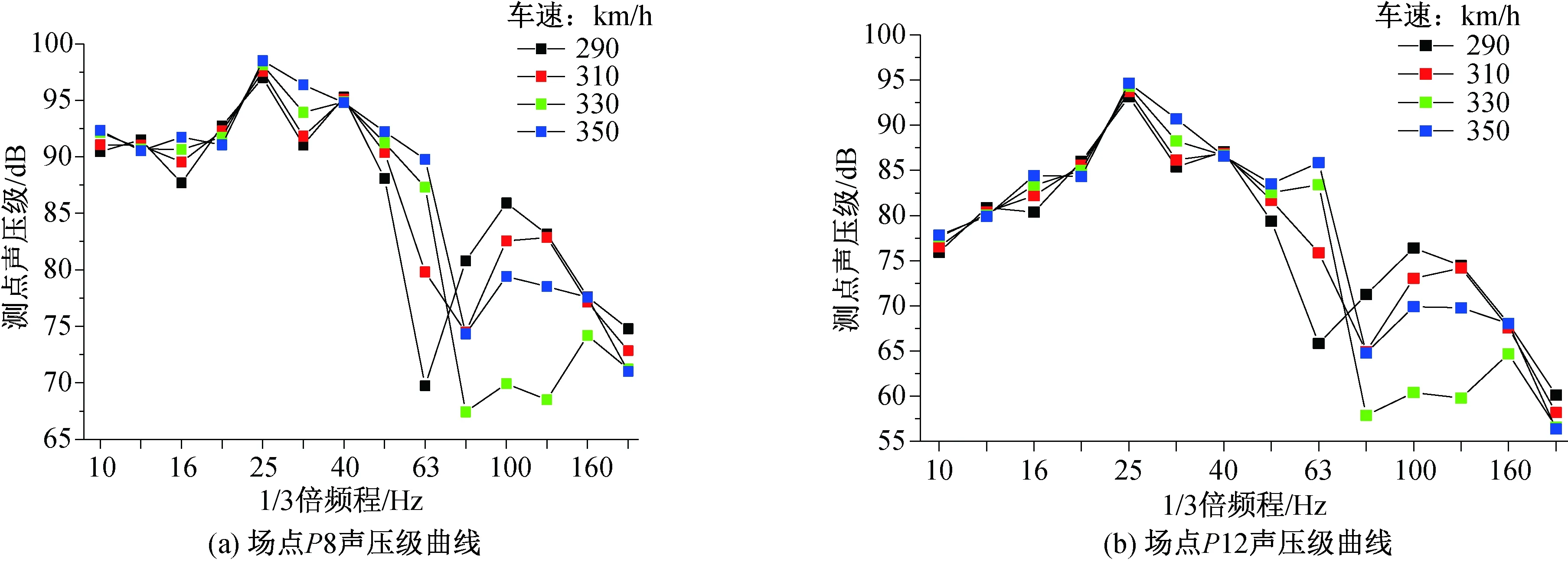
图6 不同车速对场点声压级的影响曲线Fig.6 Influence curve of different vehicle speeds on sound pressure level at field points

由图6可以看出，速度在290～350 km/h时，P8和P12场点的声压级优势频段在20～50 Hz，场点声压级随速度增加而增大，不同场点不同频段的声压级分布基本一致。

4.2 顶板厚度对噪声影响

顶板厚度由0.2～0.4 m变化时，选取场点P8、P12的声压级变化曲线如图7所示。

随着顶板厚度的增大，场点P8和P10的声压级峰值频率由25 Hz变化为31.5 Hz。场点P8在中心频率为16、63 Hz的声压幅值对顶板厚度的改变较为敏感，点P12在中心频率为16、25、31.5 Hz的声压幅值对顶板厚度的改变较为敏感。箱梁顶板厚度增大会减小场点的声压级幅值。

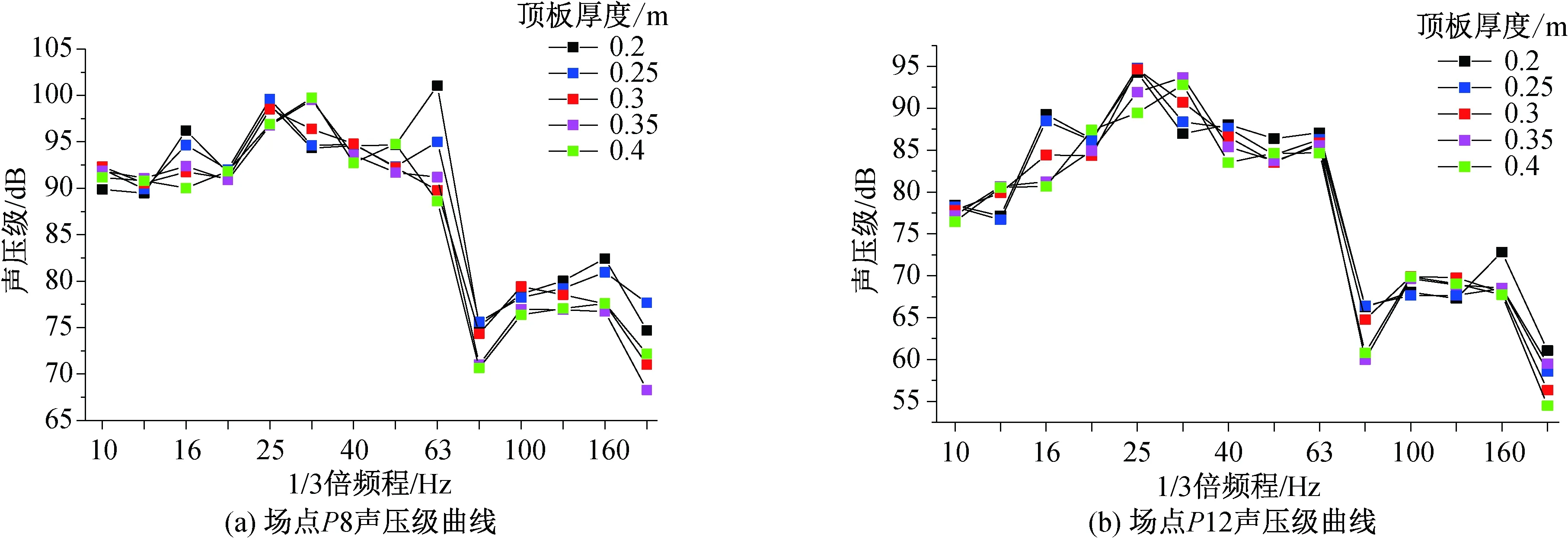
图7 不同顶板厚度对场点声压级的影响曲线Fig.7 Influence curve of different roof thickness on sound pressure level at field point

4.3 桥梁结构形式对噪声影响及贡献量分析

腔室结构不相同的桥梁，其结构噪声声辐射特性也不相同。选取单箱单室箱梁和单箱双室箱梁进行结构噪声声辐射特性分析。场点P8、P12的声压级变化曲线如图8所示。

由图8可以看出，单箱双室箱梁各场点的总声压级均小于单箱单室箱梁各场点的总声压级。顶板上方场点声压级平均减小7.19 dB，底板下方场点平均减少4.3 dB，垂直于桥梁方向横向距离25 m的场点平均减少5.8 dB。因此，采用单向双室箱梁可以有效减少桥梁结构噪声声辐射，是控制桥梁结构噪声的有效方法。

图8 各场点总声压级变化曲线Fig.8 Variation curve of total sound pressure level at each field point

为了探讨单箱单室箱梁和单箱双室箱梁在远场位置的箱梁各部分的声贡献量，单箱单室箱梁和单箱双室箱梁的各部分板件在场点P12的声贡献量情况见表2，两者对场点P12的声贡献量频谱图如图9所示。

从表2和图9中可以看出，单箱单室箱梁对P12点声压级贡献量从大到小排列依次为顶板、底板、近侧翼板、远侧翼板、近侧腹板和远侧腹板。顶板对场点的声压级贡献量最大达到了61.77%，其次是底板和近侧翼板，两者的声压级贡献量分别为14.63%和13.3%。两侧腹板的声压级贡献量最少。因此，降低顶板声辐射成为单箱单室桥梁结构减振降噪的关键。单箱双室箱梁对P12点声压级贡献量从大到小排列依次为近侧翼板、顶板、底板、远侧翼板、近侧腹板、远侧腹板和中腹板。近侧翼板对场点的声压级贡献量最大，达到了36.63%，其次是顶板和底板，两者的声压级贡献量分别为27.82%和12.74%。腹板的声压级贡献量依旧是最少的。声压级贡献量发生变化的主要原因是中腹板的存在减小了顶板的跨度，抑制了顶板的振动，导致顶板的声压级贡献量占比降低。而翼缘板却由于鞭梢效应导致声压级贡献量占比增大。因此，应尽量避免在翼缘板的边缘处安装声屏障，防止声屏障因翼缘板的振动而损坏。

表2 场点噪声线形总声压级

图9 各板件对P12点的声贡献量Fig.9 The sound contribution of each panel to P12

5 结论

1)桥梁竖向振动加速度频率主要分布在25 Hz附近，与桥梁的自振特性有关。

2)在桥梁中心线高度方向上，场点距离桥梁越近测得的噪声声压级越高。顶板振动响应比底板更剧烈，顶板的噪声辐射能力比底板强。箱梁的腹板和底板对噪声有遮蔽作用，所以底板下的噪声声压级低于顶板上的噪声声压级。在垂直于桥梁方向上，增大距离会减小场点声压级。

3)低频声场分布规则，具有单一指向性，高频场分布分散，指向性复杂，存在区域峰值，规律不明显。

4)桥梁结构噪声辐射会随着列车运行速度的增加而增加；增大顶板厚度可以有效降低场点箱梁结构的噪声辐射。

5)相同列车荷载作用下单箱双室箱梁辐射出的结构噪声声压级更小，有利于结构噪声的控制；单箱单室箱梁的顶板的声压级贡献量占比较大，声压级贡献量达到60%以上；单箱双室箱梁的顶板、底板和近侧翼缘板的声压级贡献量较为接近，顶板的声压级贡献量显著降低，近侧翼板的声压级贡献量明显增大。