改进教与学优化算法求解0-1背包问题
2022-04-06张小萍谭欢
张小萍,谭欢
(1.广西大学计算机与电子信息学院,广西 南宁 530004;2.中国移动通信集团广西有限公司,广西 南宁 530022)
教与学优化算法(TLBO)[1]是由印度学者Rao在2011年提出的一种智能优化算法,该算法模拟人类在学习过程中“教”与“学”两个学习阶段来获取知识.TLBO算法的参数少,易于理解,实现简单,具有较好的收敛性能,获得了众多学者的关注.目前TLBO算法在一些工程实践领域如测试数据生成[2]、结构可靠性优化设计[3]、太赫兹图像增强模型[4]和SRM转矩分配函数优化及控制[5]中获得了良好的寻优效果.但基本的TLBO算法仍然存在着容易陷入局部最优解,收敛速度慢的问题.
0-1背包问题(0-1 knapsack problem,0-1 KP)是一个经典的组合优化问题,在实践应用中一些优化问题如货物装箱、投资决策、材料切割和资源分配等都可以转化为0-1 KP,寻找更好的方法来求解0-1 KP,不论在理论和实践中都具有重要意义.早期,求解0-1 KP的算法主要有递归法、动态规划法、枚举法和回溯法等确定性的算法,这类算法的时间复杂度随问题规模呈指数增长,无法用于求解高维的0-1KP.近年来,随着智能优化算法的发展,众多智能优化算法应用于0-1 KP求解中,它的时间复杂度是多项式级别的,能用于求解高维的0-1 KP,但一般只能获得问题的最优解域.任静敏等[6]提出带权重的贪心萤火虫算法(WGFA),通过在基本萤火虫算法加入贪心算子、自适应权重和变异算法,提高了算法的全局搜索能力和收敛速度.孙静等[7]提出改进鸡群优化算法(ICSO),在母鸡和小鸡位置引入惯性权重,提高了算法的求解精度.陈桢等[8]提出了混合贪婪遗传算法(HGGA),在0-1 KP求解中以往的贪心算子都是使用基于价值密度比较大的的物品优先装入背包,而该算法增加了基于物品价值优先的混合选项,并增加了局部搜索模块进一步提高了寻优速度.
为了进一步提高求解0-1 KP的寻优性能,本文提出一个改进的教与学优化算法(ITLBO),在“教”阶段引入正余弦算子,在“学”阶段引入自适应惯性权重,并利用贪心算子提高全局搜索能力和算法的收敛速度.
1 0-1 KP模型
0-1 KP一般可以描述为:有一个具有承载重量限制的背包,有n件物品,每件物品有各自的重量和价值,选择若干物品装入背包,寻找一种装入方案,使得在不超过背包承载重量的情况下装入的物品价值和达到最大.0-1KP的数学模型表示为
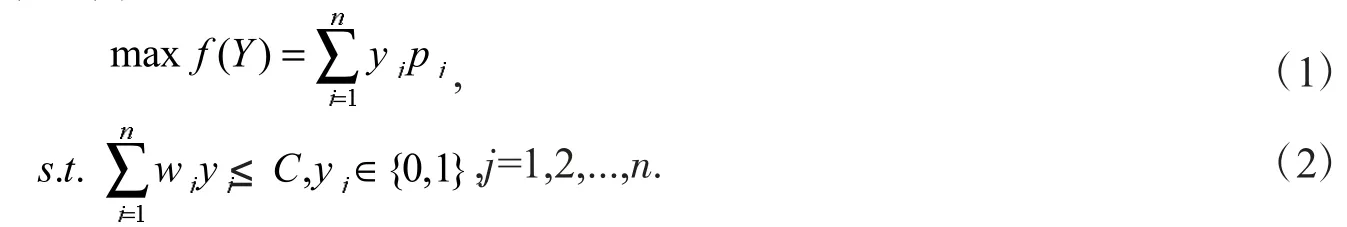
式(1)、式(2)中:n表示物品数目,C表示背包的承载重量限制,W=(w1,w2,...,wn)表示物品的重量向量,P=(p1,p2,...,pn)表示物品的价值向量.当yj=1时表示选中该物品装入背包,否则表示未装入.
2 基本TLBO
TLBO是模拟班级教学活动的优化算法,在TLBO中,1个班级代表1个种群,学员数就是种群数,学习分为“教”阶段和“学”阶段2个部分,在“教”阶段,教师引导着班级中所有学员知识水平的提高,教师是适应度最好的学员;在“学”阶段,学员获取知识主要通过学员之间的相互交流.假定求解优化问题是求最大值,TLBO的基本步骤是:
Step1初始化阶段.初始化系统参数,m是学员数目,随机初始化m位学员,Xi=(xi1,xi2,...,xin),i=1,2,...,m,n是学习的科目数,代表了问题求解变量的维数,计算所有学员的适应度.
Step2“教”阶段.选择最优(即适应度最大)的学员作为教师,用Xteacher表示,计算所有成员的平均水平Mean,每个学员都向教师学习,学习方式是利用教师和所有学员的平均水平的差异进行学习,学习过程用公式(3)、(4)、(5)来表示



3 ITLBO模型
3.1 二进制离散化
0-1 KP是二进制离散化问题,而基本TLBO是用于求解连续问题的,因此要进行二进制编码,将实数型的向量Xi=(xi1,xi2,...,xin)变为二进制向量Yi=(yi1,yi2,...,yin),编码的方式如公式(7)所示

种群中的个体由(Xi,Yi)共同表示,构成了实数向量和二进制向量构成的混合编码.
3.2 贪心算子
0-1 KP是带约束性条件的优化问题,在二进制编码之后得到的向量有可能不符合约束性条件,这些解成为不可行解.对于不可行解通常用两种方法来处理,一是使用惩罚函数,即在不可行解减去一个较大的数,使其适应度值减小,二是使用贪心算子对不可行解进行修复.测试研究表明,使用贪心算子的方法要比使用惩罚函数好,因为使用惩罚函数只是降低了不可行解的适应度使它被选中的概率降低,但没有改变不可行解的实质,而贪心算子不仅将不可行解转变为可行解,还对可行解进一步优化,将更多不超过背包承载重量的物品尽可能地放入背包,这将加快算法的收敛速度.先将物品按照价值重量比按降序排列,贪心算子(greedy operator,GO)伪代码可以表示如下:
算法1 GO

伪代码中2-6步骤的作用是修复,将不可行解转变为可行解,7-11步骤的作用是优化,在不超过背包承载重量的前提下将价值重量比大的物品优先装入背包.
3.3 正余弦算子
在基本TLBO的“教”阶段,个体更新利用的是教师和所有成员的平均值差异进行的,当算法收敛到一定阶段,进入局部最优解时,难以跳出局部最优解,为了加强算法的全局搜索能力,引入了正余弦算子.正余弦优化算法[9]是2016年提出的一种智能优化算法,利用正弦和余弦函数的周期震荡来平衡局部搜索和全局搜索,更好地实现探索阶段到开发阶段的平稳过渡.这里利用正余弦算法作为ITLBO的算子改进“教”阶段对学员更新,如公式(8)所示
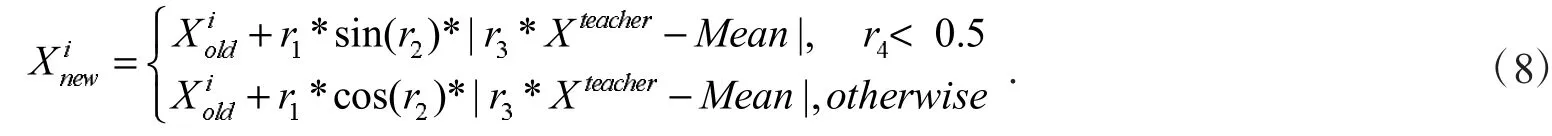
式(8)中:r1=a-a*t/T,a是一个常数,t是当前迭代次数,T是最大迭代次数,r2是[0,2π]之间的随机数,r3是[0,2]之间的随机数,r4是[0,1]之间的随机数.当正余弦函数幅度在[-1,1]之间时,进行局部搜索,当正余弦幅度大于1或小于-1时,进行全局搜索.
3.4 自适应惯性权重
对于一个好的优化算法,在迭代前期应该偏重于全局搜索,以便尽快确定最优解的范围,迭代后期偏重于局部搜索,提高寻优的精度.为了加强在“学”阶段迭代前期的全局搜索能力,引入了自适应的惯性权重.算法是否达到收敛阶段需要一定的迭代次数才能检测出来,设定一个常数cycle作为检测周期,t表示当前迭代次数且是cycle的倍数,f maxt表示当前种群的最大适应度值,当f maxt=f maxt-cycle即当前周期和上一周期的最大适应度值没有发生变化时认为种群达到收敛阶段,以此为依据将“学”阶段的更新变为公式(9)和(10)
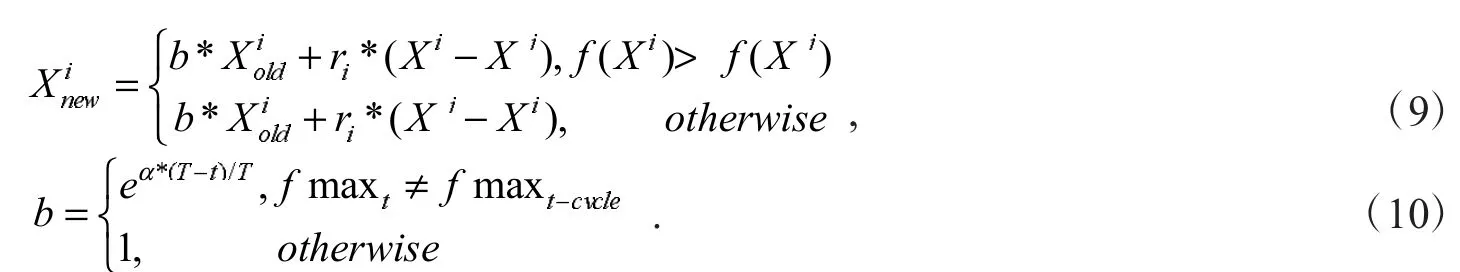
b是惯性权重,最大适应度值在一个cycle周期检测一次,在周期内b不发生变化.最大适应度值发生变化,表示种群还没收敛,公式(10)能保证b的值大于1,使得个体在一个大的范围进行全局搜索,否则b的值变为1,在一个小的范围内进行局部搜索,就平衡开发和探索的关系.
3.5 ITLBO的基本步骤
Step1初始化阶段.初始化系统参数,初始化所有学员,进行二进制编码,用贪心算子对二进制编码修复和优化,计算出所有个体的适应度值.
Step2“教”阶段.选择最优的学员作为教师,用Xteacher表示,用公式(3)计算所有成员的平均水平Mean,学习过程用公式(8)来表示,对更新后的个体编码和用贪心算子修复优化,计算出所有个体的适应度值.

4 仿真测试结果和分析
为了测试提出的ITLBO算法的性能,使用来自文献[10]提供的4个0-1背包测试案例进行仿真实验,实验环境为Windows 7操作系统,内存12 G,编程软件为Matlab2020b,使用WGFA、ICSO和HGGA作为对比算法.ITLBO中参数设定为cycle=10,α=0.7,a=2.为了避免实验的偶然性,各算法在每个案例中单独测试30次,4个算法的种群数都设为50,迭代次数为200次,分别计算各算法的最小值、最大值、平均值、方差和30次测试中能够命中理论最优值的比率,测试结果如表1所示.
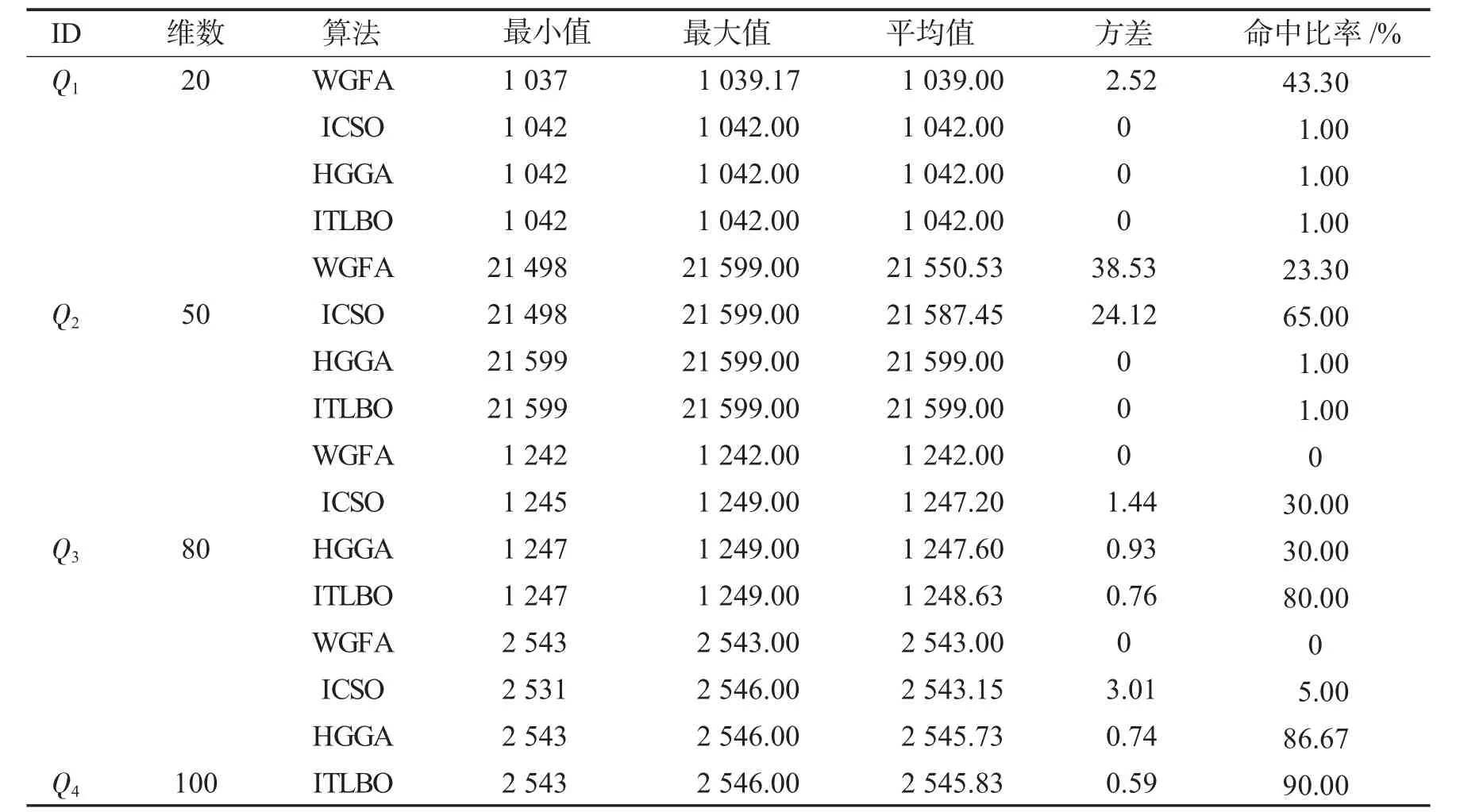
表1 仿真测试数据Tab.1 Simulation test data
从表1可以观察到ITLBO在Q1中每次都能找到理论最优值,与ICSO、HGGA性能相当,在Q2中,只有ITLBO和HGGA每次都能命中理论最优解,而随着背包问题规模的增大,在Q3和Q4中,ITLBO的平均值是4个算法中最大的,而且命中比率也是4个算法中最高,特别是在Q3中,80.00%的命中比率比第二名的30.00%的命中比率高出许多.综合分析来看,ITLBO的平均值、方差和命中比率在4个案例中都是第一或并列第一的,体现出ITLBO不论在低维和高维0-1 KP中都具有良好的寻优性能和鲁棒性.
为了进一步分析ITLBO的收敛性,利用2个高维背包问题Q3和Q4画出4个算法的平均收敛曲线,如图1和图2所示.
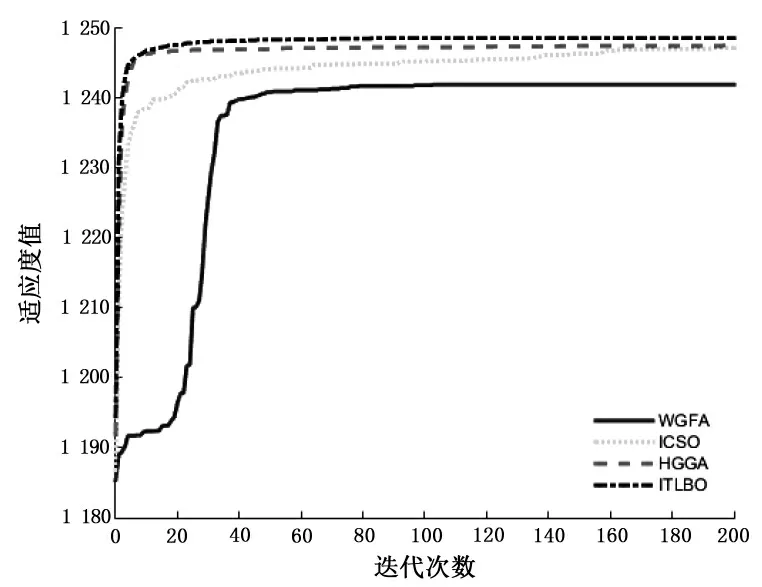
图1 Q3的平均收敛曲线Fig.1 Average convergencecurve of Q3
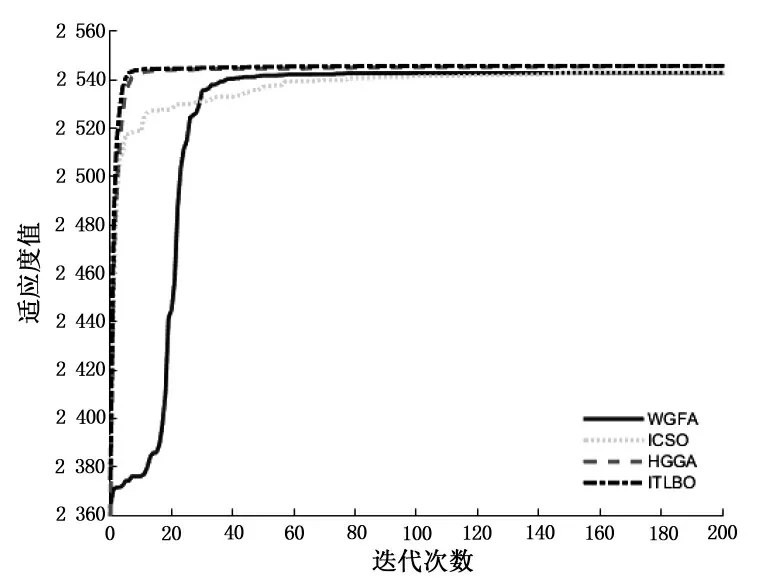
图2 Q4的平均收敛曲线Fig.2 Averageconvergencecurveof Q4
从Q3和Q4的平均收敛曲线观察到,ITLBO比ICSO和WGFA两种算法的优越性更明显,ITLBO在迭代初期就很快收敛到最优解域,虽然HGGA和ITLBO比较接近,但是ITLBO最终迭代到的解精度更高一些,说明ITLBO的收敛性更强,能很快迭代到理论最优解附近,能有效求解0-1 KP.
5 小结
文章利用正余弦算子和自适应的惯性权重改进了基本TLBO算法用于求解0-1 KP,使算法在迭代过程的“教”阶段和“学”阶段都能平衡开发和探索的关系,并通过利用贪心算子,能够加快算法的收敛速度,可以较快地搜索到全局最优解,避免进入局部最优解,并且具有较强的鲁棒性.
