基于两级权重的多视角聚类

杜国王 周丽华 王丽珍 杜经纬

(云南大学信息学院 昆明 650500)

(dugking@mail.ynu.edu.cn)

随着数字传感器的快速增长和社交网络的广泛应用，数据获取的方式和渠道越来越多样化.同一事件或样本可以从不同的视角收集不同类型的数据，对于单模态的数据也可以提取多种特征来描述样本，例如可以从图像中提取颜色、纹理等多种特征以捕获比例、遮挡、照明及旋转变化，从而提高图像识别的鲁棒性[1].通常，从不同视角收集的数据既包含一致性信息也存在互补性信息，综合考虑不同视角之间的关联信息有助于提高数据分析的性能.由于现实中多视角数据的标签难以获取，因此多视角聚类作为一种无监督学习方法受到众多研究者的关注.

多视角聚类旨在融合多视角数据中蕴含的一致性和互补性信息，据此将样本划分为簇，使得同一簇中样本间的相似度高，不同簇中样本间的相似度低.根据不同的划分策略，现有的多视角聚类算法大致可以分为基于重构的、基于图的、基于k-means的和基于信息瓶颈的4类.基于重构的多视角聚类算法主要使用非负矩阵分解或自编码技术[1-6]完成聚类，其主要思想是通过重构原始数据寻找样本的低维表征，然后基于低维表征进行聚类分析.基于图的多视角聚类算法[7-11]在每个视角内构造近邻图，然后将基于各个视角的近邻图融合为一个公共的近邻图，最后基于公共的近邻图完成聚类.基于k-means的多视角聚类算法[1,5,10,12-13]在各个视角内独立进行k-means聚类，然后融合各个视角的聚类结果为最终结果.基于信息瓶颈的多视角聚类算法[14-15]通过将不同视角中的数据对象压缩到一个“瓶颈变量”中，同时最大化地保存数据所蕴含的信息量以获取数据对象间的内在模式.

虽然现有的多视角聚类算法能够取得较好的聚类结果，并广泛应用于众多领域，但它们没有同时考虑视角内描述样本的不同特征的重要性和同一样本在不同视角内的权重.实际上，多视角数据通常具有高维性，而这些高维特征中又仅有部分特征对聚类有较大贡献，并且当数据非常稀疏时，数据重构过程会过多关注0元素的贡献，使得学习的低维表征不能很好地近似原始数据；同时数据稀疏性也会导致样本间距离度量不准确，以致每个视角内构造的近邻图不能合理地刻画样本间的相似性.因此，现有的多视角聚类算法在稀疏数据中难以获得较好的聚类性能.另外，同一样本在不同的视角中对聚类的贡献也可能不同，在一个视角内位于簇中心的样本在另一个视角内可能位于簇边缘.因此，有效区分视角内不同特征的权重和同一样本在不同视角内的权重是提高多视角聚类性能的重要因素.

文献[13,16-17]提出了基于加权k-means的策略来学习视角内每个特征的权重，但是它们没有考虑数据稀疏性问题，因此特征权重的分配不一定合理.文献[1,5,10,13]考虑了不同视角的权重，但是它们将每个视角的权重作为相应视角中所有样本的权重，没有区分每个样本在不同视角中的不同重要性.此外，许多聚类算法独立处理表征学习和聚类，即首先提取多视角特征，然后使用k-means或谱聚类等传统聚类算法获得聚类结果.这种分离式学习策略没有很好地利用多视角表征学习与聚类之间的关系，也会导致聚类效果不理想.最近，深度嵌入聚类(deep embedding clustering, DEC)[18]设计了一个聚类嵌入层，将表征学习和聚类融为一体，协同训练、相互促进，进一步提升了聚类性能.然而，DEC模型只适用于单视角数据，在多视角数据的每个视角上独立使用DEC模型虽然能够完成聚类，但是由于没有融合蕴含在多视角数据中的关联信息，聚类性能往往不尽人意.

本文提出了一种基于两级权重的多视角聚类(multi-view clustering based on two-level weights, MVC2W)算法，该算法设计了特征级和样本级的权重策略，引入特征级和样本级注意力机制学习视角内每个特征的权重和每个样本在不同视角内的权重.两级注意力机制的引入使得算法在训练过程中能够更加关注重要的特征和重要的样本，能够合理融合不同视角的信息，从而有效克服数据高维性和稀疏性对聚类结果的影响.同时，MVC2W引入了DEC模型中的聚类嵌入层[18]，将表征学习和聚类融为一体，协同训练，进一步提高多视角聚类的性能.

本文的主要贡献概括为3个方面：

1) 提出了一种基于两级权重的多视角聚类算法MVC2W，该算法设计了特征级和样本级的权重策略，层次化地区分了多视角数据中2种信息的权重.同时引入聚类嵌入层，将表征学习和聚类融合在一起，协同训练、相互促进.

2) 引入特征级注意力机制和样本级注意力机制学习特征级和样本级权重，使算法在训练过程中能够更加关注重要的特征和重要的样本，合理融合不同视角的信息，有效克服数据高维性和稀疏性对聚类结果的影响.

3) 在5个稀疏程度不同的数据集上进行了大量实验，实验结果表明，本文所提的MVC2W算法的聚类性能均优于11个基线算法，尤其是在稀疏程度较高的数据集上，MVC2W的聚类性能的提升更加显著.

1 相关工作

1) 基于重构的多视角聚类算法.文献[2]提出了基于非负矩阵分解的多视角聚类(multi-view clustering via nonnegative matrix factorization, Multi-NMF)算法，该算法通过最小化每个视角的系数矩阵与一致性矩阵之间的差异来学习一致性矩阵并获得聚类结果；为了捕获每一个视角的局部几何信息，文献[3]结合图正则约束[19]和MultiNMF，提出了基于图正则非负矩阵分解的多视角聚类(multi-view clustering via graph regularized nonnegative matrix factorization, MultiGNMF)算法；文献[5]结合概念矩阵分解[20]和图正则[19]约束，提出了基于图正则概念矩阵分解的多视角聚类(multi-view clustering via concept factorization with local manifold regularization, MVCC)算法，该算法能够自动学习每个视角权重；文献[1]提出了基于深度半正定矩阵分解的多视角聚类(deep matrix factorization multi-view clustering, DMF-MVC)算法，该算法通过多层的半正定矩阵分解以消除来自不同视角的干扰因素，达到仅将聚类信息保留在最后表征层的目的，同时DMF-MVC也设计了权重学习策略来捕获不同视角的重要性；文献[6]联合学习每个视角的表征，并使用新的嵌套自编码器框架将各个视角的表征编码为完整的潜在表征(autoencoder in autoencoder networks, AE2-Net)，从而灵活地融合来自每个视角的内在信息.

上述多视角聚类算法主要使用了非负矩阵分解或自编码技术，其中一些算法也能够学习不同视角的权重.然而，这些算法均没有考虑每一个视角内表征的多样性，这在很大程度上影响了多视角聚类的效果.虽然文献[4]利用基于协同正交约束的非负矩阵分解(non-negative matrix factorization with co-orthogonal constraints, NMFCC)捕获每一个视角内部的多样性，但是它没有区分同一样本在不同视角中的不同贡献.

2) 基于图的多视角聚类算法.多视角数据的不同视角之间往往蕴含一些互补信息，文献[9]将子空间聚类扩展到多视角聚类(diversity-induced multi-view subspace clustering, DiMSC)，并利用希尔伯特-施密特独立标准(Hilbert-Schmidt independence criterion， HSIC)作为多样性正则项来约束近邻矩阵之间的互补性；文献[7]提出了一种不需任何参数即可自动学习权重的多图学习框架(auto-weighted multi-view graph learning, AMGL)；文献[8]提出了一致性多图多视角聚类(multiview consensus graph clustering, MCGL)算法，该算法在每一个视角内通过秩约束学习图矩阵，然后将各个视角学习到的图矩阵优化为一个全局图，最后通过拉普拉斯图约束优化全局图；文献[21]提出了一种基于自适应结构概念矩阵分解的多视角聚类(adaptive structure concept factorization for multiview clustering, ASMV)算法，对全局图的拉普拉斯矩阵施加秩约束，以实现理想的近邻分配，并且通过学习视角权重和无监督降维的自适应图来融合不同视角的信息，以获得最优聚类结果.

3) 基于信息瓶颈的多视角聚类算法.文献[14]提出了一种双重加权的多视角聚类(dual-weighted multi-view clustering, DWMVC)算法，通过互信息自动学习视角权重，并将这些权重施加到基于内容和上下文的多视角数据表示上，使2种数据表示的视角互补信息得以充分利用；文献[15]提出了基于信息瓶颈的无冗余多视角聚类(non-redundant multi-view clustering based on information bottleneck, NrMIB)算法，该算法基于信息瓶颈最大化数据中的信息，确保高质量的聚类结果，同时通过最小化聚类结果与已知数据划分模式之间的互信息，降低冗余.

4) 基于k-means的多视角聚类算法.文献[16]同时学习视角和特征的重要性，提出了基于加权k-means的多视角聚类(TW-k-means)算法，但是该算法忽略了视角之间的相互关系；文献[12]提出了基于特征选择的加权多视角聚类，将特征级和视角级权重方案引入多视角聚类任务；文献[13]提出了融合特征级和视角级两级权重的协同k-means多视角聚类(two-level weighted collaborativek-means for multi-view clustering, TWCOKM)算法，该算法通过加权策略学习每个特征和每个视角的重要性，同时以协作方式设计目标函数，从而有效地发现嵌入在多视角中的公共结构.

表征学习和聚类的融合.文献[22]提出了一种基于深度神经网络和k-means的聚类框架(deep clustering network, DCN).在t-SNE[23](t-distributed stochastic neighbor embedding)启发下，DEC[18]采用了一个深度栈式自编码(stacked autoencoder, SAE)[24]初始化特征提取模型，然后通过自训练目标分布迭代优化基于KL(Kullback Leibler)散度的聚类目标.与表征学习和聚类分离的方式相比，这些联合学习算法展示出极大的优越性.但是，目前的研究主要是单视角数据的聚类，对于多视角数据中表征和聚类的联合学习尚末深入研究.

目前，在多视角聚类框架中，如何学习视角内每个特征的权重和同一样本在不同视角内的权重，以及如何联合聚类和表征学习仍然是一个开放性的问题.近年来，注意力机制由于能够捕获数据中的重要信息，已经被广泛应用于自然语言处理[25]、图像识别[26]和图数据分析[27].同时，自编码[28]由于能够无监督地学习数据中的非线性结构，已经成为表征学习和数据降维的主流方案之一.本文提出的算法MVC2W结合了注意力机制和自编码模型.与MVC2W相关的算法是AE2-Net，TWCOKM，DWMVC.AE2-Net和MVC2W都是基于自编码的深度多视角聚类，但是AE2-Net并没有考虑2种类型的权重.TWCOKM虽然考虑了特征级权重，但是TWCOKM不能很好地处理稀疏度高的数据.DWMVC利用互信息度量每个视角的权重，但是忽略了特征级权重.MVC2W同时考虑了特征级和样本级的权重，能够有效应对高维特征和数据稀疏问题.另外，MVC2W引入了DEC框架，将表征学习和聚类融合在一个统一的框架中，协同训练、相互促进.

2 基于两级权重的多视角聚类

本节首先给出多视角聚类的相关定义，然后详细介绍所提的MVC2W多视角聚类算法.

2.1 问题定义

定义1.多视角数据.设{X(v)∈表示M个视角中的N个样本，其中X(v)∈N×d(v)表示第v个视角的特征矩阵，d(v)表示第v个视角的特征维度.表示第v个视角中的第i个样本.表示第v个视角内第i个样本的第j个特征.

定义2.多视角聚类.给定多视角数据{X(v)∈多视角聚类通过结合不同视角的特征信息，将N个样本划分为C个簇，同一簇内样本间的相似度高，不同簇间样本的相似度低.

2.2 MVC2W多视角聚类算法

本文所提的MVC2W多视角聚类算法设计了两级权重策略，能够层次化地学习视角内各个特征的权重和同一样本在每个视角内的权重，以缓解数据的高维及稀疏问题.MVC2W算法的整体结构如图1所示，其中包含了3个组件:1)特征级权重组件.该组件设计了基于特征级注意力机制重构的自编码器，用于学习视角内每个特征的权重并获得每个视角的低维表征.2)样本级权重组件.该组件利用样本级注意力机制学习每个样本在不同视角中的权重，并对样本在每个视角内的低维表征进行加权求和，以获得样本的公共表征.3)聚类嵌入层[18]组件.该组件联合优化样本的公共表征和聚类分布，并基于样本的聚类分布为样本分配簇标签.

Fig. 1 The overview of MVC2W图1 MVC2W算法整体结构

2.2.1 特征级权重组件

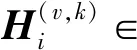
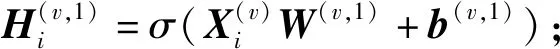
(1)

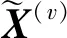
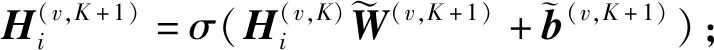
(2)

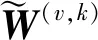
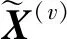
(3)

通过最小化式(3)，每个视角内优化的自编码能够平滑数据流形信息并保存样本之间的相似性[29].然而，式(3)同等对待每个特征对于损失函数的贡献，忽略了视角内不同特征往往具有不同重要性的事实.此外，当数据的稀疏程度非常高时，解码器重构过程中0元素会得到更多关注.因此，对非0元素与0元素在重构误差中施加不同权重，将式(3)的损失函数修正为

(4)

其中，B(v)∈N×d(v)表示第v个视角的权重矩阵，⊙表示逐元素相乘.

对于权重矩阵B(v)的选取，本文提出了3种方案.第1种方案将与X(v)中特征值为0的元素对应的项赋值为0，将与X(v)中特征值为非0的元素对应的项赋值为β>0，即:

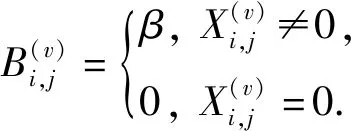
(5)

这种方案完全抑制了特征值0的贡献.然而，这些特征值0虽然导致了数据的稀疏性，但是完全抑制它们的贡献也不尽合理.因此第2种方案将与X(v)中特征值为0的元素对应的项赋值为α>0，即:

(6)

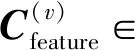
(7)

基于注意力机制重构的损失函数定义为

(8)

2.2.2 样本级权重组件

通常，多视角数据中不同的视角提供了不同的语义，同一样本在不同的视角中对于聚类的贡献可能不同.为此，本文引入样本级注意力机制，自动学习每个样本在不同视角中的权重.

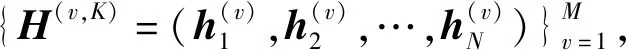
(9)

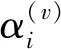
(10)

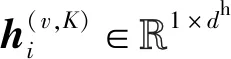
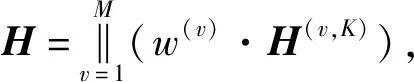
(11)

2.2.3 聚类嵌入层组件

受DEC[18]的启发，本文引入聚类嵌入层将表征学习和聚类融合在一起，协同训练、相互促进.

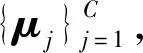
(12)

由于样本的簇标签是未知的，因此定义一个目标分布来辅助优化聚类.目标分布P可以基于软聚类分布Q=[qi,j]∈N×C进行计算，P中的元素pi,j的计算方式为

(13)

聚类嵌入层的损失函数定义为分布Q和P之间的KL散度:

(14)

聚类嵌入层可以看作是一种自监督训练模块，该模块通过分布Q计算目标分布P，进而，分布P又用于监督分布Q的更新.最后，基于qi,j(j=1,2,…,C)的值，分配样本i的簇标签yi∈{1,2,…,C}为

(15)

N个样本的簇标签向量表示为y=(y1,y2,…,yN).

4.4 在该工程钢筋混凝土不等肢剪力墙结构中，增大了连梁刚度。但不等肢联肢墙的抗震研究尚有很多问题，在今后的研究中会得到更好的解决。

2.3 整体损失函数

联合优化3个组件，MVC2W算法整体的损失函数为

(16)

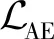
2.4 模型优化

图1所示模型的优化过程包括预训练和微调训练2个步骤.

预训练采用Adam优化器完成，主要用于初始化模型，学习率设定为10-3，所有数据样本作为一个批次训练每个视角的自编码器.其中，特征级和样本级注意力机制以及聚类嵌入层并不参与预训练.

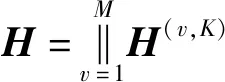
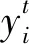
(17)

其中，N是样本总数.

MVC2W算法如算法1所示，利用深度学习框架Tensorflow实现该算法，其运行环境为Ubuntu 16.04和1080ti显卡以及64GB内存.

算法1.MVC2W算法.

输入:多视角数据{X(v)∈学习率l、平衡参数λ、迭代停止阈值δ、迭代次数epochs、聚类数目C、目标分布更新间隔T；

输出:聚类结果y.

③t=0；

④ Repeat

⑤ 根据式(12)计算软聚类分布Q；

⑥ if (t%T==0) then

⑦ 根据式(11)～(13)更新目标分布P；

⑧ end if

⑨ 根据式(15)计算簇标签y；

⑩ 根据式(17)计算连续2次迭代中簇标签发生变化的样本比例g；

3 实验评估

3.1 实验设置

1) 数据集.为了验证MVC2W算法的聚类效果，本文选取了5个真实数据集进行实验.5个数据集分别为BBC,BBCSport,NGs，HW2Source，100Leaves.数据集的统计信息如表1所示:

Table 1 The Statistics of Datasets表1 数据集统计信息

表1中BBC，BBCSport数据集中的文档分别从BBC新闻网站和BBCSport网站收集，文档分为田径、板球、足球、橄榄球和网球5个类；NGs中文档的3个视角对应于数据预处理的3种特征提取方法；HW2Source中的2个视角对应于MNIST和USPS这2个手写体数字(0～9)源；100Leaves包含100种植物，每种植物有16个样本，每个样本从纹理、边距和形状3个视角进行描述.

本文使用每个视角内所有样本稀疏度的平均值作为每个视角的稀疏度.每个样本的稀疏度使用稀疏度算子[30]进行度量，该算子计算为

(18)

其中，d表示样本的维度，x=(x1,x2,…,xn)表示需要计算稀疏度的样本.当样本x仅包含一个非0分量时，样本x的稀疏度为1;当样本x的所有分量均相等时，样本x的稀疏度为0.稀疏度数值越大，表明数据越稀疏.5个数据集中各个视角的稀疏度如表2所示.从表2可以看出，HW2Source和100Leaves这2个数据集在各个视角的稀疏度较低，但是BBC，BBCSport，NGs这3个数据集在各个视角的稀疏度都非常高.

Table 2 Sparseness of Different Views of Datasets表2 数据集不同视角的稀疏度

2) 对比算法.本文实验的对比算法选取了11种流行的多视角聚类算法，包含6种基于重构的算法(MultiNMF[2]，MultiGNMF[3]，DMF-MVC[1]，MVCC[5]，AE2-Net[6]，NMFCC[4])，3种基于图的算法(ASMV[10]，DiMSC[9]，MCGL[8])，1种基于k-means的算法(TWCOKM[13])以及1种基于信息瓶颈的算法(DWMVC[14]).实验中所有对比算法的代码均从各文献的作者个人主页下载，并根据原论文建议的参数区间，调整所有对比算法的相应参数，使其获得最优结果.在MVC2W算法中，设置λ=0.1，每个视角内的自编码器采用5层结构，网络结构均设置为[d(v)，512，32，512，d(v)]，其中d(v)是指每个视角数据的输入维度.所有算法使用的相关参数如表3所示：

Table 3 Related Parameters of Algorithms表3 算法的相关参数

3) 估指标.本文采用聚类分析中常用的2种指标，即准确度(accuracy，ACC)和规范化互信息(nor-malized mutual information,NMI)，评价所有算法的聚类效果.ACC和NMI的值越大，则表示聚类效果越好.

3.2 聚类结果

为了避免实验过程中随机初始化带来的干扰，实验结果均由相关算法在每个数据集上运行10次得到的均值和标准差组成.表4和表5展示了12种算法在5个数据集上的ACC和NMI，其中粗体表示最好的聚类结果，括号内的值表示标准差.

从表4和表5可以看出，MVC2W在BBC，BBCSport，100Leaves数据集上均获得了最高的ACC和NMI值，并且与次高ACC和NMI值相比，MVC2W在3个数据集上的ACC和NMI值分别提高了9%和15%、9%和9%、12%和6%.尽管在HW2Source和NGs数据集上MVC2W没有取得最好的聚类结果，但是它的效果仅次于最好的MCGL和DWMVC.实验结果表明：MVC2W提出的两级权重策略是有效的.

从表4和表5中也可以看出，DMF-MVC，MVCC，MCGL，ASMV的聚类效果较差.这些算法虽然学习了每个视角的权重，但是它们均忽略了视角中各个特征的权重.TWCOKM在稀疏度低的数据集上聚类效果较好，但是对稀疏度高的数据集，TWCOKM的聚类效果变差.说明TWCOKM不适用于稀疏度高的数据集.

DWMVC在NGs数据集上获得最好的聚类结果，但是在其他4个数据集上的聚类效果均低于MVC2W.AE2-Net也是基于自编码器的多视角聚类算法，但是并没有获得良好的聚类结果，这是因为它没有考虑数据中的稀疏因素.这些实验结果进一步表明MVC2W算法提出的两级权重的有效性.

基于非负矩阵分解的多视角聚类算法(MultiNMF，NMFCC，MultiGNMF)与基于概念矩阵分解的多视角聚类算法(MVCC)相比，MVCC在稀疏度高的数据集上聚类结果较好，这是因为MVCC算法虽然没有明确考虑稀疏关系，但是它的损失函数使算法在重构过程相当于采用了基于式(6)(β=1)的权重方案.

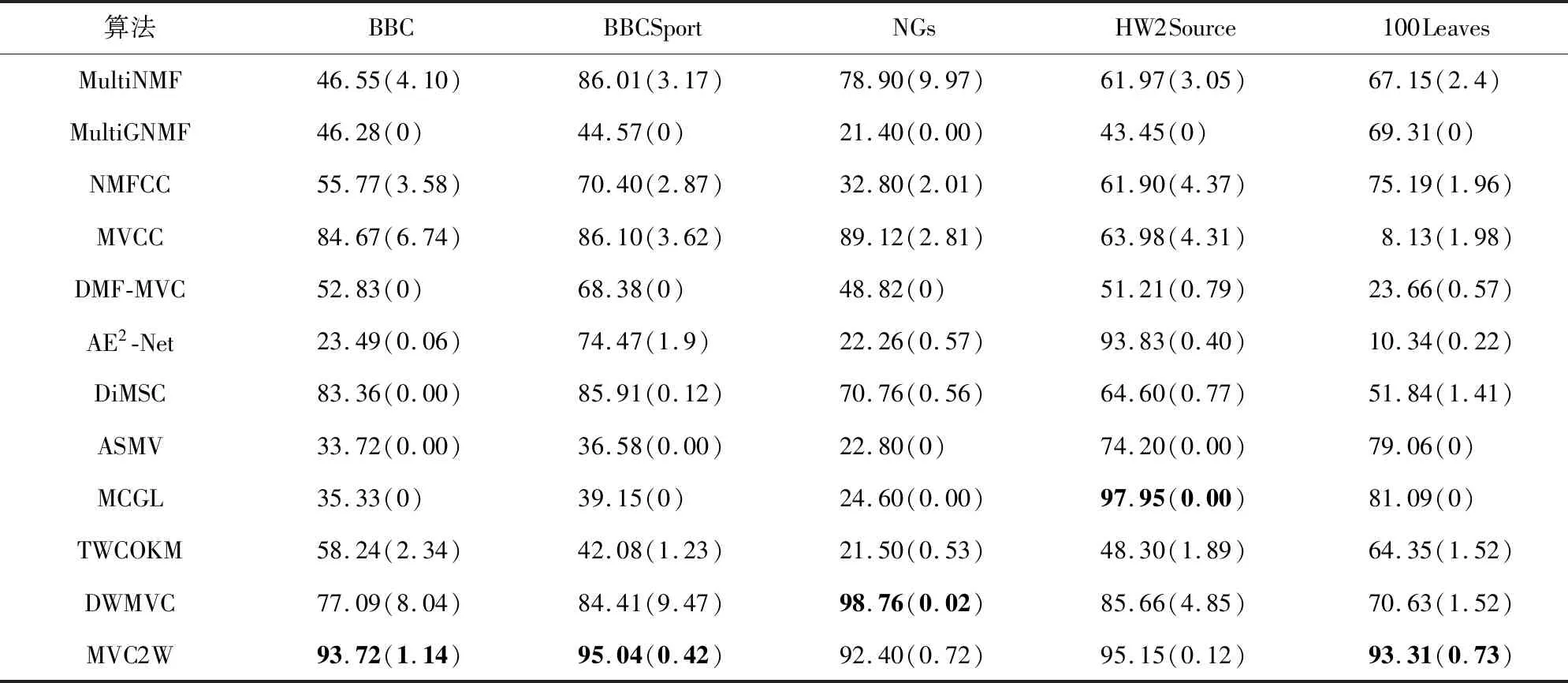
Table 4 ACC of Various Algorithms on All Datasets表4 所有数据集上各种算法的ACC

Table 5 NMI of Various Algorithms on All Datasets表5 所有数据集上各种算法的NMI

基于图模型的多视角聚类算法MCGL和ASMV在稀疏度低的数据集上能够获得较好的聚类结果，尤其是MCGL在HW2Sources上获得了最好的聚类结果，但是2种算法在稀疏度高的数据集上的聚类结果普遍不好.这是由于数据过于稀疏时，近邻图的计算会产生较大误差，不能很好地度量样本之间的近邻程度.与此类似，MultiNMF和NMFCC在稀疏度高的数据集上优于MultiGNMF，也是由于数据过于稀疏使得构造的近邻图不能准确保存样本间的流形关系，从而降低了聚类结果.与MCGL和ASMV相比，DiMSC在稀疏度高的数据集上聚类结果较好，这也是因为DiMSC计算每个视角的近邻图方式相当于考虑了基于式(6)(β=1)的权重方案.

3.3 消融研究

为了进一步验证两级权重的有效性，本节提出了MVC2W的4个变种算法:1)MVC2WNo-W.不使用权重方案.2)MVC2W1.使用基于式(3)的损失函数，选择第1种权重方案(式(4)).3)MVC2W2.使用基于式(3)的损失函数，选择第2种权重方案(式(5)).4)MVC2WNo-SA.使用基于式(8)的损失函数，但是不加入样本级权重.4个变种算法的参数λ均设置为0.1，MVC2W1和MVC2W2的参数β设置为10，MVC2W2的参数α设置为1.MVC2W和4个变种算法的ACC和NMI如表6和表7所示.

从表6和表7可以看出，在稀疏度高的数据集上，与MVC2WNo-W相比，加入权重方案的算法的聚类性能都有较大提升，说明3种权重方案对于稀疏数据建模都是有效的.但是在稀疏度低的数据集上，与MVC2WNo-W相比，MVC2W1和MVC2W2的聚类结果在HW2Source数据集上提升很小且在100Leaves上变得更差.在式(5)(6)的权重重构方案中，式(6)的聚类效果更好，这是由于式(5)虽然增大了非0元素的权重，但是直接忽略了所有0元素对于损失函数的贡献，而式(6)在增大非0元素权重的同时还考虑了0元素对于损失函数的贡献.与式(6)的权重方案相比，基于特征级注意力的权重方案在大部分数据集上均获得了更好的聚类结果，表明基于特征级注意力权重的有效性.并且相对于式(5)(6)的权重方案，基于特征级注意力机制的权重方案不需要人为选择权重β，更有利于实际应用.与MVC2WNo-SA，相比，MVC2W在多数数据集上都能够获得更好的聚类结果，验证了样本级注意力机制的有效性.

Table 6 ACC of MVC2W and Four Variant Algorithms表6 MVC2W和4个变种算法的ACC

Table 7 NMI of MVC2W and Four Variant Algorithms表7 MVC2W和4个变种算法的NMI

3.4 样本级权重分析

MVC2W算法能够学习同一样本在不同视角中的权重.本节以BBC和BBCSport数据集为例，进一步探索样本级权重的重要性.

1) 聚类结果和视角级注意力权重的相关性.本实验使用当前视角中所有样本注意力权重的平均值作为不同视角的注意力权重.图2(a)(b)展示了在不同视角中进行聚类时获得的ACC和相应视角的注意力权重.从图2(a)(b)可以发现，图2(a)中第1个视角的ACC最小，视角注意力权重最低；第2个视角的ACC最大，视角注意力权重值最高;在图2(b)中，第2个视角的ACC最小，视角注意力权重最低；第1,3,4个视角的ACC较大，这3个的视角注意权重值也较大.从以上结果可以看出，视角注意力权重和ACC之间存在正相关关系:当视角注意力权重大时，相应视角的聚类结果ACC高；当视角注意力权重小时，相应视角的聚类结果ACC低.这说明了设置视角级权重的合理性.

2) 样本级权重.在图2(c)(d)展示了2个数据集的前10个样本在不同视角中的注意力权重.从图2(c)(d)可以看出，同一样本在不同视角内的权重是不一样的.由于本文提出的样本级注意力机制能够更好地学习到每个样本在不同视角中的权重，因此能够获得更好的聚类结果.

Fig. 2 View attention weights and sample attention weights图2 视角注意力权重和样本注意力权重

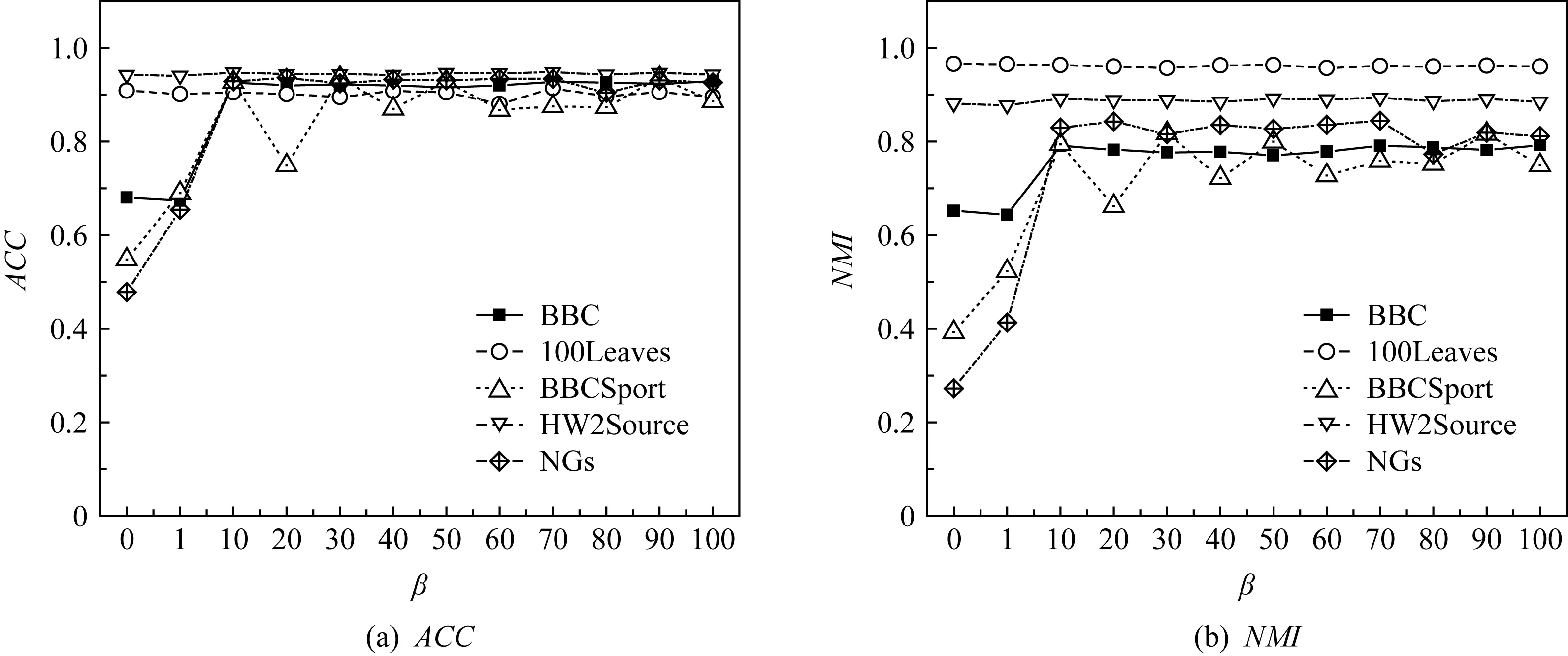
Fig. 3 ACC and NMI under different β图3 β取不同值时所获得的ACC和NMI

3.5 参数分析

MVC2W2算法需要人为选择3个参数λ，α和β.在DEC[18]的实验中，当λ=0.1时，聚类结果良好，因此本文设置λ=0.1.本节主要探索当α=1时，参数β对于聚类结果的影响.权重β用于控制重构过程中对于0元素的惩罚程度.β越大，表示越倾向于重构非0元素.

图3示例了MVC2W2算法中ACC和NMI随β变化的情况.从图3可以看出，在稀疏度低的数据集上，β的改变对于ACC和NMI影响不大；而对于稀疏度高的数据集，当β=0时结果相当差，当β=1时实验效果也并不佳.这是因为虽然在一定程度上惩罚了0元素，但是由于数据稀疏度较高，0元素在重构中所占的比重还是相当大;当β增大到10以后，除了BBCSport，其他数据集的聚类结果都较好，并且性能平稳；当β增大到70以后，聚类性能又下降，这是因为当权重β特别大的时候，相当于忽略了0元素，MVC2W2算法退化成为MVC2W1算法.本实验表明，在进行表征学习时，应该更加关注训练网络中非0元素的重构误差，但是也不能完全忽略0元素的重构误差.因此，对于β的选取，本文建议选择10.

3.6 低维表征维度

本节主要研究在保持其他层大小不变的情况下，MVC2W算法聚类结果如何随着低维表征维度dh大小而变化.使用不同大小的维度dh∈{4，8，16，…，256}构建聚类算法，当dh=16时，每次为dh增加16构建新的算法，以此类推，直到dh=256.在BBC数据集上执行聚类实验，不同维度dh的聚类结果如图4所示.

Fig. 4 ACC and NMI under different dh on BBC图4 BBC数据集上dh取不同值时所获得的 ACC和NMI

从图4可以看出，随着dh增大，ACC和NMI先增加，然后降低，这是由于当dh太小时，数据信息被过度压缩，导致低维表征无法保存视角中的有效信息;当dh太大时，低维表征包含了冗余信息，不利于聚类.当dh=32时，聚类结果最好，因此，在实验中对于BBC数据集选择{512，32，512}作为隐藏层结构.与此类似，在BBCSport，NGs，100Leaves，HW2Sources的实验中本文也使用了{512，32，512}的网络结构.

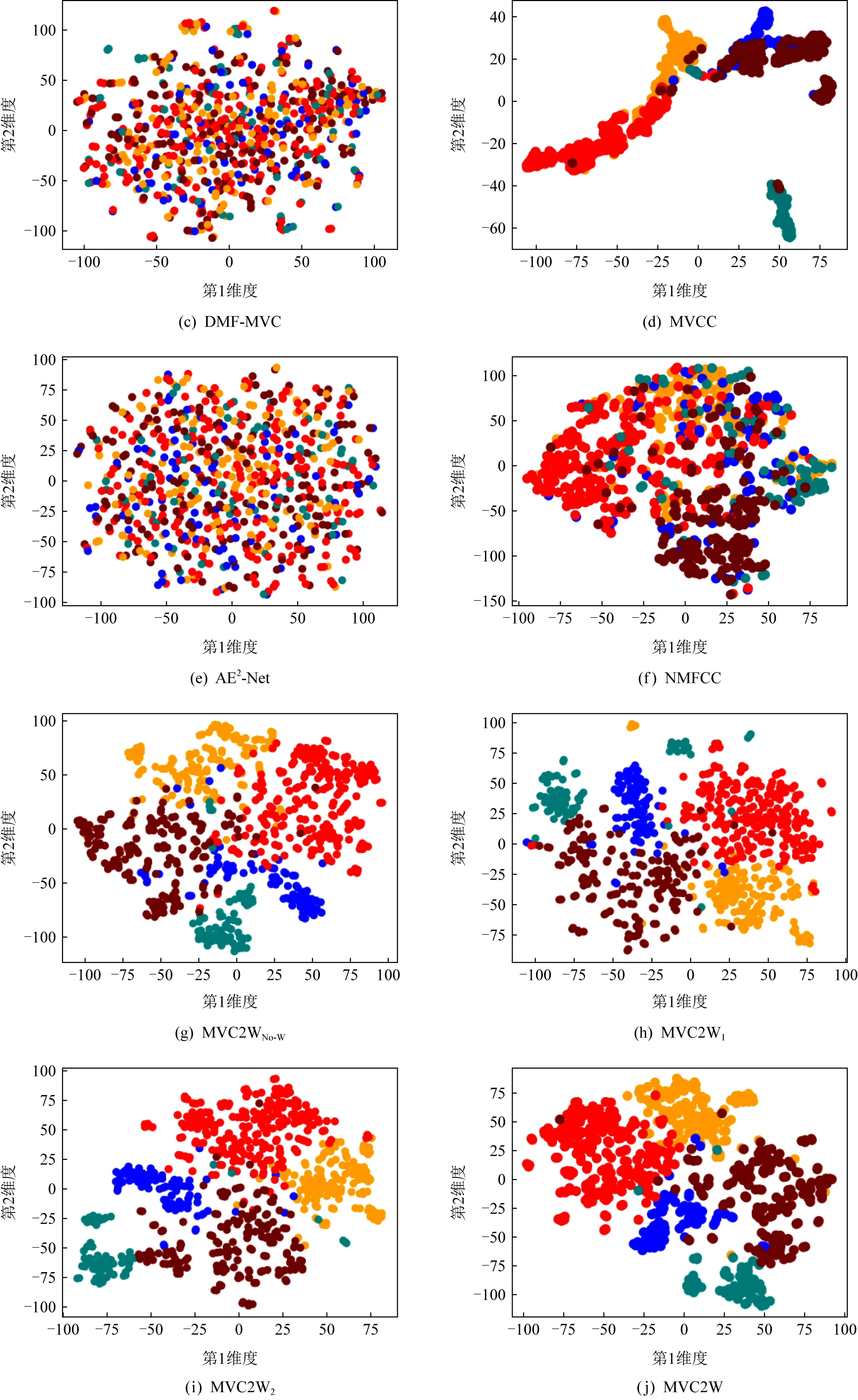
Fig. 5 Visualizing BBC dataset图5 可视化BBC数据集

3.7 可视化分析

为了进一步验证MVC2W是否能够学习到具有判别性的低维表征，本节使用t-SNE[23]将MVC2W和基于重构的多视角算法在BBC数据集上学习得到的低维表征投影到2维空间进行可视化，相应的可视化结果示于图5，图5中不同的簇用不同的颜色进行标记.

从图5中可以看出，图5(g)～(j)中相同颜色的样本点明显比图5(a)～(f)中更集中，能够显示出簇的大致轮廓，而图5(a)～(f)中不同颜色的样本点则较为分散.虽然图5(d)中相同颜色的样本点也较为聚集，但是不同颜色的样本点之间重叠度非常高，尤其是棕色和蓝色的点均存在大量重叠.这说明MVC2W系列算法学习到的低维表征比其他算法学到的表征有更好的判别性.

在图5(g)～(j)中，图5(g)中相同颜色的样本点显得有些分散，而图5(h)～(j)中相同颜色的点更为集中且轮廓更加明显，这说明权重方案的有效性.对比图5(h)(i)，可以发现图5(i)中棕色的样本点更加分散且绿色样本点分散为2簇，而图5(h)中棕色和绿色的样本点更加紧凑，说明使用式(6)权重方案的聚类算法比使用式(5)权重方案的聚类算法获得的表征有更好的区分度，进一步说明了在分配特征权重时不能够忽略数据中的0元素的信息.与图5(g)～(i)相比，图5(j)中样本点更加紧凑和集中，并且簇的轮廓也更加明显，进一步证明了基于注意力机制的权重方案的有效性.

4 结论

本文提出了一种基于两级权重的多视角聚类算法MVC2W.该算法能够同时学习视角内每个特征的权重和每个样本在不同视角内的权重，使得训练过程中能够更加关注重要的特征和重要的样本，更加合理地融合不同视角的信息，从而有效克服数据高维性和稀疏性对聚类结果的影响.在5个稀疏程度不同的数据集上的实验结果表明，MVC2W算法的聚类效果比11个基线算法均有提升，尤其是在稀疏程度高的数据集上，MVC2W的提升更加显著，说明MVC2W能更好地适用于稀疏数据集.同时，消融实验也说明了两级权重的有效性，与4种变种算法相比，MVC2W在不同稀疏程度的数据集上能够获得良好的聚类结果.并且MVC2W算法自动学习视角内每个特征的权重，更易于在实际中应用.

本文在学习样本的公共表征时，将每个视图的低维表征简单地加权串联.在未来的工作中，我们将采用更加高效的学习方法来融合多个视图的低维表征，比如施加协同正则约束或HSIC约束，以最大化视角之间的关联.另外，多视角数据在收集过程中可能存在缺失.如何在有缺失的数据中进行有效聚类也将是我们下一步的研究重点.

作者贡献声明：杜国王设计并实现所提算法，完成实验并撰写论文;周丽华提出指导性意见并修改论文;王丽珍指导实验方案的完善及结果分析；杜经纬收集、整理实验数据.