城市快速路互通立交分流区交通冲突预测模型

2022-04-04张卫华

公路工程 2022年1期

张卫华，陶虎，陈乾

(合肥工业大学汽车与交通工程学院，安徵合肥 230009)

快速路承载着城市的主要交通量，多条快速路相交形成的互通立交作为快速路主要组成部分，其立体隔离式的空间多层结构保证了各个方向交通流的独立性，减少了车辆间不必要的交织行为，提高了交通运行效率和安全性。快速路分流区的交通流特征与基本路段完全不同，不同道路选择的交通流频繁换道、相互交织，导致较高的事故风险，快速路较高的车速也使得事故的严重程度较高[1-2]。

HIDAS[3-4]建立微观仿真的换道模型，分析研究了不同运行状态下快速路交织区的交通特征、换道行为、交通冲突等，对仿真结果评价后发现多数情况下该模型与传统模型仿真效果相似，但其适用性更广。TARKO[5]的研究中提到了诸多常用的交通冲突的判别指标，其中大多为时间度量的判别指标。唐超[6]、郑展骥[7]等以TTC为基础，对分、合流区和交织区的冲突预测，以及安全评价等进行了研究。马艳丽[8]等构建了冲突的识别模型，并通过不断调整阈值进行计算后发现，合理的阈值选择对提高交通冲突识别的准确率有很大的帮助。NATIO[9]以数学建模，以及仿真为研究手段，发现车辆之间发生碰撞的概率与速度、车头时距等有密切的关联，速度越高则碰撞概率越大，并以此建立了一个最优速度模型。孙璐[10]等通过分析仿真后的交通冲突数据，发现交织区交通冲突数与交通量呈正相关，与交织区车道数呈负相关。

此前学者的研究多以高速公路为对象，且大多只集中于冲突数量这单一维度上，而那些可以丰富交通冲突形成机理研究的重要组成部分，如冲突发生的位置、冲突车辆交通运行特征等方面的研究较少。针对上述不足，本文围绕城市快速路互通立交的分流区，充分分析冲突发生的各项特征，探究冲突发生的深层机理。

1 分流区数据调查与处理

1.1 交通调查地点与时间

本文以城市快速路互通立交的分流区为研究对象，调查获得交通流特征，调查地点的选取应满足以下条件：① 道路构造形式要有普遍性，且交通流运行状态简单，同时外界干扰因素要尽可能地减少；② 交通量大并具有明显的时间差异性；③由于使用无人机进行航拍调查，因此还需满足视野开阔，无电磁干扰，无禁飞和限飞要求。通过对某市城区快速路互通立交进行筛查后，选取某立交南侧分流区为调查对象，车流行驶方向为由南向北，见图1。

图1 数据采集点无人机航拍图

为保证数据的准确性和统计分析的便利性，无人机航拍视频要求图像稳定清晰，交通到达相对均匀。经选择后的每段视频时长均为3 min，且其中包含了早高峰、晚高峰和平峰3个时段。

1.2 基础数据处理

通过Matlab将视频逐帧转化为图片，利用图像识别技术对每一张图片中车辆的像素点位进行获取。并通过像素-实际长度的比例尺关系将像素点位映射到实际空间，从而求得车辆速度、车道速度和断面速度等交通流特征。

考虑在发生追尾冲突与换道冲突时所涉及车辆间的不同时空特征，选择TTC模型、PET模型分别用于判定追尾冲突和换道冲突，冲突发生的指标分别选取为TTC≤6 s、PET<5 s[11-12]。以此统计分流区的冲突个数如下：分流区通过车辆数1 120辆，追尾冲突数33，换道冲突数122。

2 分流区交通冲突特征研究

2.1 交通冲突与交通量关系特征

2.1.1交通流率与千车冲突率关系分析

将交通量与冲突数进行拟合，两者呈指数函数关系y=1.582×e0.018 x，决定系数R2>0.9，说明拟合效果极好。但当每辆车发生冲突的概率一定时，驶过分流区车辆数目的增加自然会引起交通冲突数的增加。因此，为探究车辆冲突概率与交通量的关系，可引入单位车量冲突数的概念，将其与交通流率进行比较分析，故本文设置变量千车冲突率γ，如式(1)所示：

(1)

式中:C为交通冲突数；Q为交通量。

图2所示的千车冲突率与交通流率拟合曲线方程为y=0.061 4x-26.852(R2=0.72)，千车冲突率与交通流率呈正相关关系，说明冲突发生的概率随着交通流率的上升而不断增加。

图2 交通流率与冲突率拟合曲线

2.1.2车头时距与交通冲突特性分析

车头时距是衡量交通运行状态、表征交通特征的重要微观指标，按照是否发生冲突将所有车辆分为2组，分别为冲突组和非冲突组，并对比分析冲突组、非冲突组车头时距与交通冲突之间的关系，结果如表1、图3所示。

根据表1可知，冲突组车辆间的平均车头时距显著低于非冲突组(P=0<0.05)，较小的车头时距体现了较大的交通流率，因此这从一定层面也再一次反映了交通量对交通冲突的影响。由图3可知，车头时距小于17.5 s时，冲突组车辆的车头时距曲线低于非冲突车辆；但当车头时距大于17.5 s时，冲突组曲线戛然而止，此时车辆将不会再被卷入冲突。说明车头时距越小，车辆行为越会受到限制，被卷入冲突的可能性越高。

表1 冲突组与非冲突组平均车头时距对比分析Table 1 The comparison of average headway between vehi-cle conflictied and vehicle non-conflicted车头时距均值/s(标准差/s)tp冲突组车辆3.31(2.69)-3.412**0非冲突组车辆4.09(3.72)

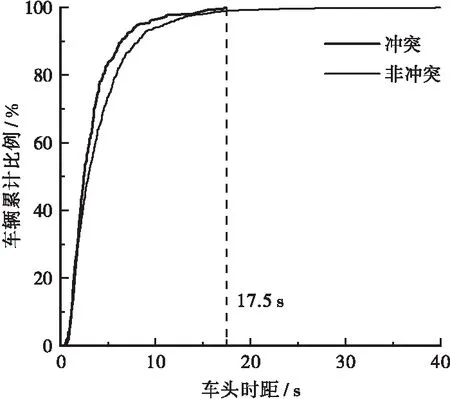
图3 冲突组与非冲突组车头时距分布对比(对图形横纵坐标做了调换)

2.2 交通冲突与速度关系特征

2.2.1车道速度与交通冲突特性分析

车辆进入快速路分流区后便会产生不同的道路选择，不同道路选择导致分流区内车辆加、减速，以及换道行为频发，交通状态混乱，车辆间行驶速度差异。分别对分流区主线速度、匝道速度与冲突发生之间的关系进行研究，结果如图4所示。车道速度与交通冲突的发生之间有着明显的规律，不论主线还是匝道，当车道平均运行速度越低时，千车冲突率越大，车辆发生交通冲突的概率越高。

(a) 主线速度

由于车道平均运行速度与车道上驶过的交通量之间有着密切的关系，速度越低往往说明此时的交通量越大。因此，为了排除分析车道速度与交通冲突关系时交通量的影响，利用SPSS对千车冲突率进行控制变量的偏相关分析，结果如表2所示。

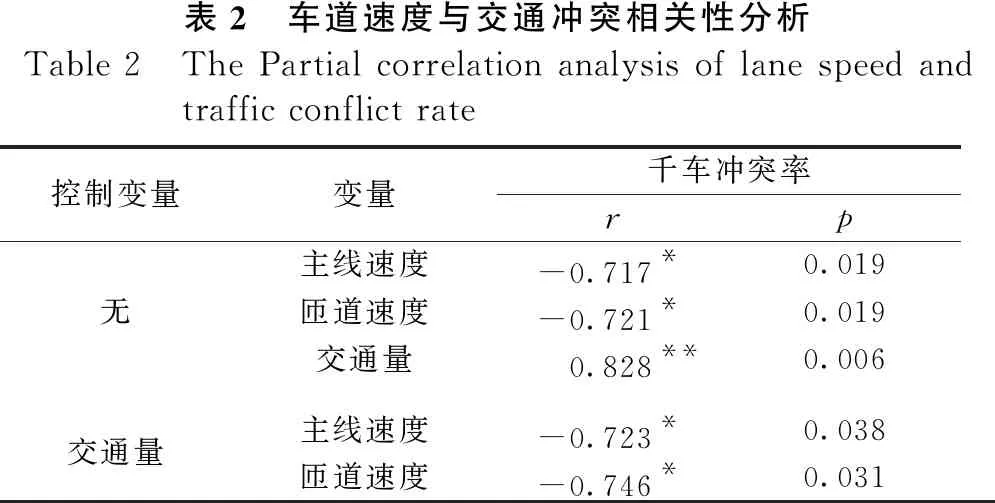
表2 车道速度与交通冲突相关性分析Table 2 The Partial correlation analysis of lane speed and traffic conflict rate控制变量变量千车冲突率rp主线速度-0.717*0.019无匝道速度-0.721*0.019交通量0.828**0.006交通量主线速度-0.723*0.038匝道速度-0.746*0.031

分析结果显示，当不进行变量控制时车道速度(不论主线还是匝道速度)与交通冲突发生间存在着负相关关系；而交通量与交通冲突发生之间存在着正相关关系，且相关性更强。因此选择交通量作为控制变量进一步探究车道速度与冲突的关系，结果显示两者间负相关性依然存在。以上分析说明了速度确实是影响冲突发生重要因素，即在车辆正常行驶的速度范围内，提升速度可以减少冲突的发生。

2.2.2车辆速度与交通冲突特性分析

为了探究车辆速度与交通冲突之间的具体关系，将调查车辆依旧按照交通冲突是否发生分为冲突与非冲突2组，通过t检验分别对2组车辆速度特征进行分析。结果如表3所示，冲突车辆的速度显然小于非冲突车辆。冲突车辆与非冲突车辆速度分布区间如图5所示。

表3 冲突与非冲突组之间车辆速度t检验Table 3 Independent t-test of speed between vehicles con-flicted and vehicles non-conflicted分组速度均值/(km·h-1)(标准差)tp冲突组49.1(10.24)-7.901**0.000非冲突组55.2(10.87)

图5 冲突车辆与非冲突车辆速度分布对比

冲突车辆的速度落在20～80 km/h的区间内，主要集中于30～60 km/h，平均值为49.1 km/h；相比而下，非冲突车辆的行驶速度分布区间更广，且集中分布在40～70 km/h区间，均值也明显更高，达到55.2 km/h，分析结果表明分流区车辆速度与冲突间存在相互影响的关系。

2.3 交通冲突与换道行为关系特征

换道行为是微观驾驶行为的重要组成部分，且同样是诱发交通运行状态波动的重要原因，因此将车辆的换道行为纳入交通冲突特性研究具有重要意义。

为了研究与行文表述的便利性，对分流区车道进行编号和功能区划分，将车道按照车辆行驶方向由左向右依次编号，则主线车道分别为L1、L2和L3，匝道的车道为L4和L5，并规定其中较为特殊的渐变段车道为L4。对研究区域以每10 m一个单位区块进行划分，同时将断面结构与功能相近的若干个单位区块合并，称作一个功能区间。因此230 m长的分流区则被划分为4个功能区间，分别为：分流上游区、分流渐变区、分流导流区和分流下游区，具体情况如下表4、图6所示。

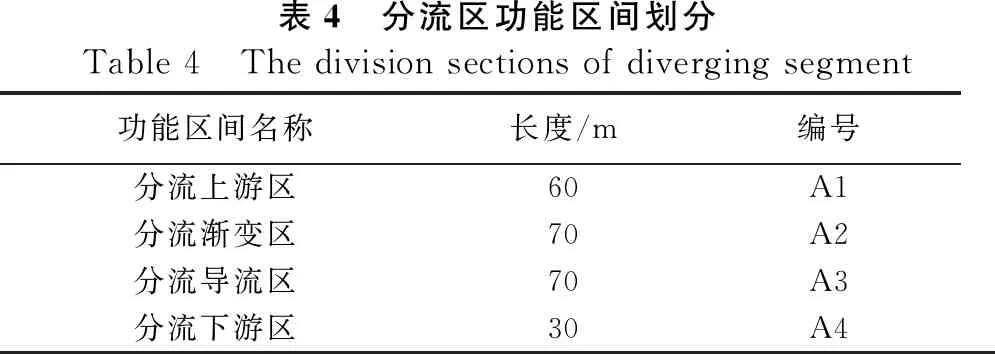
表4 分流区功能区间划分Table 4 The division sections of diverging segment功能区间名称长度/m编号分流上游区60A1分流渐变区70A2分流导流区70A3分流下游区30A4

图6 功能区间划分断面位置示意图

2.3.1冲突与非冲突组车辆换道行为分析

分流区上游一般有多条主线车道，从不同车道驶入的车辆进入分流区，对道路路线选择也不同，其换道需求也有所差异。为了更好地研究换道行为与交通冲突之间的关系，按照驶入分流区时车辆所占的车道编号对冲突组车辆，以及非冲突组车辆进行了进一步的分组。采取独立t检验，从换道次数的角度出发，对不同车道驶入分流区的冲突与非冲突车辆进行比较分析，结果如表5所示。

由表6可知，不论车辆由L1、L2、L3中哪条车道驶入分流区，冲突组车辆与非冲突组车辆在换道频次上都有着显著的差异，其中由L1和L2车道驶入分流区的车辆发生冲突的风险随换道频次的增加而不断上升，而从L3驶入分流区的车辆发生冲突的风险却并不随着换道频次的增加而上升。也就意味着驶入车道位置，以及换道频次是诱发交通冲突的重要因素。

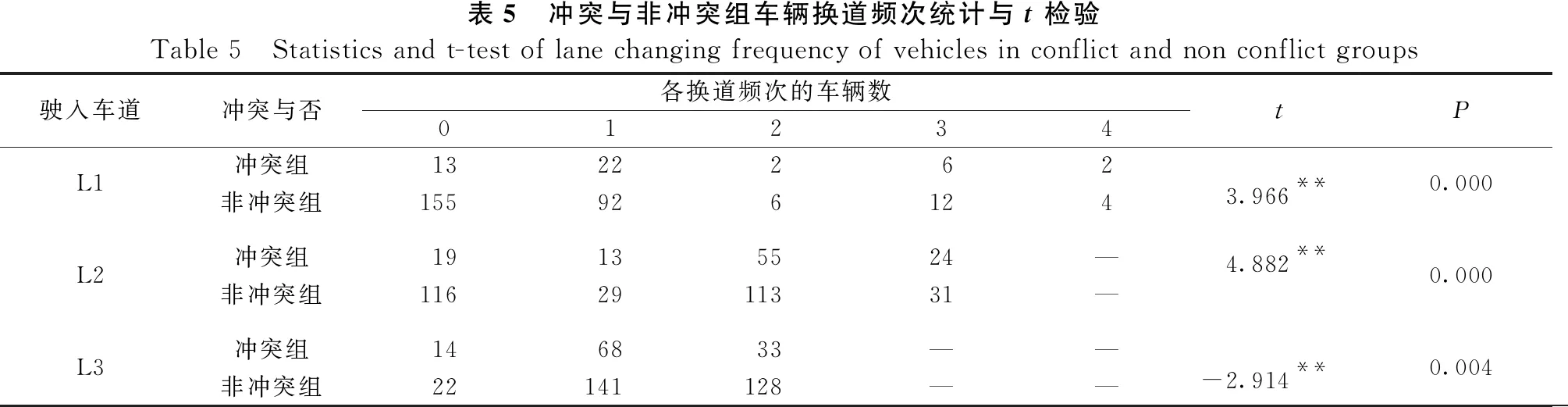
表5 冲突与非冲突组车辆换道频次统计与t检验Table 5 Statistics and t-test of lane changing frequency of vehicles in conflict and non conflict groups驶入车道冲突与否各换道频次的车辆数01234tPL1冲突组13222 623.966**0.000非冲突组155926124L2冲突组19135524—4.882**0.000非冲突组1162911331—L3冲突组146833——-2.914**0.004非冲突组22141128——

2.3.2区域换道发生频次与冲突发生之间的关系

为了探究区域换道与冲突之间的关系，我们对分流区的空间进行进一步细分，按照前文划分的功能区间和车道将整个分流区细分为17个小的区域，并按照功能区间编号在前、车道编号在后的规则对其进行命名，如A1L2，该区域即代表着分流上游区A1区间内L2车道的部分。对每一个区域内的交通冲突数和换道频次进行统计，并对比、分析区域换道行为对冲突发生所产生的影响。为保证对比分析结果的准确性，应将区域内发生的每一次换道行为都纳入考虑，如在分析A1L2区域内冲突与换道关系时，除要考虑A1区间中的车辆由其他车道换入L2车道的行为外(即车辆在A1区间内由L1车道换入L2的行为和由L3车道换入L2的行为)，还应考虑车辆由L2向其他车道的换出行为。采取Spearman检验对不同类型冲突与换道行为之间进行相关性分析，结果如表6所示。

表6 不同类型冲突与换道行为间相关性分析Table 6 The correlation analysis between different types of traffic conflict and lane changing behavior换道行为与冲突RSP追尾冲突0.3710.140换道冲突0.530*0.029

根据表6分析可知，区间内追尾冲突发生数对换道频次的影响并不显著(P=0.140>0.05)，说明换道行为的发生并不会引发追尾冲突；但换道冲突则不同，其发生次数与换道频次之间有着明显的联系，两者呈正相关关系(P=0.029<0.05.)，说明换道行为对于换道冲突有显著的影响。但是研究区域换道行为对换道冲突的影响不能只从数量这单一维度出发，还需考虑不同区域换道冲突对换道行为的敏感性。因此，引入换道冲突-换道比这一变量用来表征换道冲突对换道行为的敏感性，即单位换道次数引发的换道冲突次数。各区域换道频次和换道冲突-换道比的关系如图7所示，其中横坐标各区域编号按换道冲突-换道比由小到大的规则依次排列。

图7 各区域换道频次与换道频次-换道比关系图

由图7柱状图可知，A2L3和A2L4是主线车辆向匝道分流(即车辆L3与L4之间的换道行为)的主要区域，此区域内的换道频次分别为631和432，远高于其他区域，但换道冲突-换道比却并不高。由图7中的折线图可知，换道冲突-换道比较高的5个区域(从高到低依次分别为：A1L3、A4L2、A1L1、A3L2、A2L1)均分散分布于主线上，且每个区域内换道频次都很低，平均只有58.8，说明发生在主线上的换道行为对冲突发生的影响更大，安全隐患也更高；特别是在换道冲突-换道比最高的A1L3区域内，由于进入分流展宽区之前混合车流中意图主线继续行驶的车辆与即将分流车辆之间频繁的交织行为，严重地影响了周边车辆的正常行驶，也因此带来了更频繁的换道冲突。

3 交通冲突预测模型建立

为了预测一定交通状态下不同行驶特征的车辆于分流区行驶时发生冲突的概率，根据冲突与非冲突车辆运行特征的分析结果，选择对冲突发生有显著影响的宏观因素为自变量构建冲突预测的二分类Logstic模型。

3.1 二分类Logistic模型

二分类Logistic回归模型的因变量取值个数为2，因此对于交通冲突是否发生这类二分类问题的拟合与分析具有非常好的适用性。

Logistic回归模型为：

(2)

其中，p为结果发生的概率预测值；β0，β1，…，βk为待估未知参数，由式(2)可得：

(3)

对所有影响因素进行事前检验，筛选出对因变量有显著影响的自变量,是进行二分类Logistic回归分析前的必要工作，常用的方法为比分检验法(Socore Test)。

3.2 分流区交通冲突预测模型

将二分类Logistic模型的应变量取值0和1来表示代表冲突的发生与否。自变量的选择中，驶入分流区时的车道编号、换道发生次数、数据采集时间点为分类变量，须将分流比和表征交通运行状态等连续变量按一定规则划分为分类变量。对上述变量进行筛选后，最终驶入分流区车道位置、换道发生次数和行程车速(分类变量)可被纳入模型。变量取值和划分如表7所示。

表7 经Score Test检验筛选后自变量的描述和取值Table 7 The discription and assignment of independent variable screened by Score-test method影响因素变量赋值驶入分流区车道x10=由L1车道驶入,1=由L2车道驶入,2=由L3车道驶入换道发生频次x20=未发生换道,1=换道1次,2=换道2次,3=换道3次,4=换道4次行程速度x30=速度在15%分位以下,1=速度在15%～85%分位之间,2=速度在85%分为以上

将上述自变量纳入二分类Logistic模型中进行计算，便可得到如表8所示的模型估计结果。对模型的估计结果进行拟合度检验后发现，其似然卡方值约为90，显著水平也小于0.01，同时Hosmer-Lemeshow检验的显著水平值为0.424，大于0.05，表明了模型具有良好的有效性和准确性，且缺陷较小。

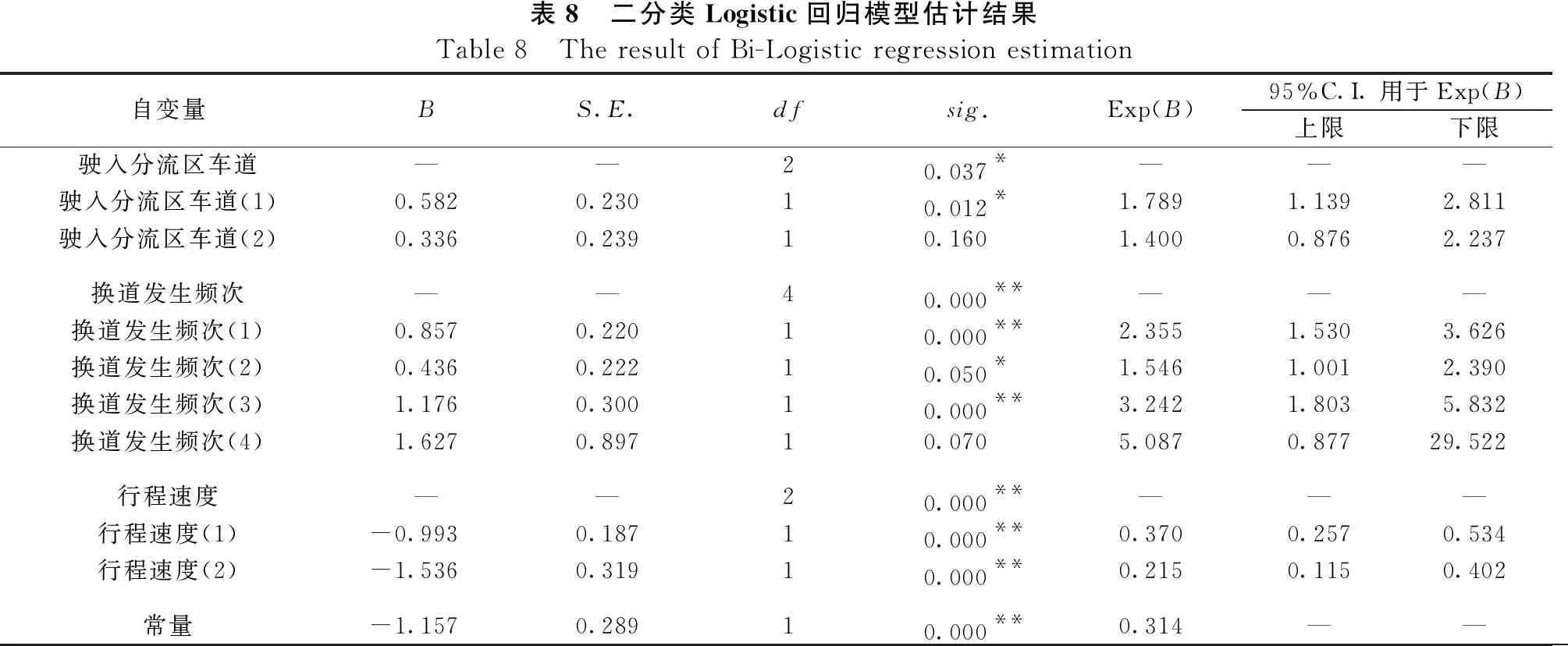
表8 二分类Logistic回归模型估计结果Table 8 The result of Bi-Logistic regression estimation自变量BS.E.dfsig.Exp(B)95%C.I.用于Exp(B)上限下限驶入分流区车道——20.037*———驶入分流区车道(1)0.5820.23010.012*1.7891.1392.811驶入分流区车道(2)0.3360.23910.1601.4000.8762.237换道发生频次——40.000**———换道发生频次(1)0.8570.22010.000**2.3551.5303.626换道发生频次(2)0.4360.22210.050*1.5461.0012.390换道发生频次(3)1.1760.30010.000**3.2421.8035.832换道发生频次(4)1.6270.89710.0705.0870.87729.522行程速度——20.000**———行程速度(1)-0.9930.18710.000**0.3700.2570.534行程速度(2)-1.5360.31910.000**0.2150.1150.402常量-1.1570.28910.000**0.314——

如果将该二分类Logistic回归模型模型预测值p>0.5作为发生交通冲突的临界值，对本文1 046例样本进行交通冲突发生与否的预测，发现模型的准确预测率高达76.5%，因此本文建立的冲突预测模型具有良好的适配性。

根据表8可得分流区交通冲突预测模型如下：

p(y=1)=

(4)

式中:x1(1)表示变量x1取值为1即车辆由L2驶入分流区；x2(1)表示变量x2取值为1即换道1次；x2(2)表示变量x2取值为2即换道2次；x2(3)表示变量x2取值为3即换道3次；x3(1)表示变量x3取值为1即行程速度落在15%～85%分位之间；x3(2)表示x3取值为2即行程速度高于85%分位。

表8的结果显示，由L1车道驶入分流区的车辆发生交通冲突的概率最低；而由L3驶入分流区的车辆比L1驶入的车辆发生交通冲突的风险高1.4倍；由L2驶入的车辆发生冲突风险最高，是由L1驶入分流区车辆的1.789倍。从换道频次的角度来看，交通冲突的风险与换道频次之间呈正相关关系，未发生换道行为的车辆冲突风险最小，换道频次为1的车辆发生交通冲突的概率比未换道车辆高近2.4倍，换道频次为2的车辆发生冲突概率略高于未换道车辆，为约1.55倍；换道频次为3和4的车辆发生冲突概率是未换道车辆的3.2倍和5.1倍，由此可见，车辆频繁的换道行为极易引发交通冲突。

同样，行程速度也显著影响交通冲突发生的概率，随着速度不断提升,交通冲突概率不断降低，0～15%分位速度组发生冲突的可能性最大；如果以0～15%的低速组作为参照，中速度组中(即车辆速度落在15%～85%区间，以此类推，85%～100%分位为高速度组)，冲突概率是低速组的25.7%；而高速度组中车辆发生冲突的概率最低，仅约1/9。这反映了在快速路中，低速车辆显著地影响了分流区交通运行的安全性，速度越低安全隐患越高。