非对称高墩连续刚构桥跨中合龙顶推力研究

任 翔， 余 兴， 王 璐， 张洪斌， 张 玥， 宋 飞

(1.西安科技大学 建筑与土木工程学院, 陕西 西安 710054； 2.中国铁建大桥工程局集团有限公司, 四川 成都 610500)

0 引言

当预应力混凝土连续刚构桥中跨合龙温度高于设计合龙基准温度[1-2]时，温降将使主梁收缩引起主墩发生水平偏位。为消除桥墩偏位和主梁在温降产生的不利影响，常在中跨合龙前，以预先在合龙口施加水平顶推力的方式进行补偿。合龙口顶推前需要确定拟顶推位移、顶推力和顶推时机等关键要素。准确计算合龙口拟顶推水平位移是保证顶推过程中结构始终处于安全受力状态和改善成桥后结构线形、内力处于最优状态的重要保障，而获得合龙口顶推位移与顶推力的关系，是确定合龙口顶推力的前提基础。

目前，对连续刚构桥实施合龙口顶推的相关研究有不少的报道。梁勇旗[3]对多跨高墩连续刚构桥合龙方案和合龙段顶推力进行研究，计算分析不同合龙方案的理论顶推量，推导了相应的顶推力，对比分析了不同合龙方案的变形和内力，确定了最佳的合龙方案。李军[4]等针对黔江某特大预应力连续刚构桥进行顶推力和顶推位移计算。采用有限元分析方法，分析中跨顶推合龙施工对该桥梁成桥状态的位移、应力状态的影响。李杰[5]等分析合龙口不同顶推力作用下成桥阶段主梁的水平位移，讨论合龙温度对顶推力和梁体水平位移的影响。杨国俊[6]等基于力法原理提出一种适用于单柱式墩连续刚构桥先边跨后中跨合龙的顶推力解析计算方法，并以工程实测结果进行验证。SHAN[7]等推导了连续刚构桥中跨合龙时合龙口顶推力与墩顶位移的解析公式。吴峰[8]等以顶推过程中桥墩截面应力为约束条件，基于多目标线性规划方法对合龙段顶推力进行求解。计算时忽略顶推力对主梁混凝土徐变的影响，考虑其对桥墩混凝土徐变的影响，通过线性迭代计算获得非线性最优解。杨孟刚等[9]推导双肢薄壁塔-梁固结矮塔斜拉桥在顶推阶段和正常使用阶段的桥墩裂缝宽度与顶推力的关系式，由此确定合龙顶推力的取值范围，在此基础上考虑合龙温差对顶推力进行修正。伍英[10]等利用多目标线性规划方法确定合龙顶推力，考虑顶推力对混凝土收缩徐变的影响，得到的合龙顶推力可使运营阶段桥墩截面拉应力最小。

以山西省新建兴保地方铁路安家山河预应力混凝土连续刚构桥合龙顶推施工为工程背景，采用数值解析结合有限元法的分析方法，对不同墩高、不同桥墩截面形式的连续刚构桥中跨合龙口顶推力与顶推位移的关系进行研究，对比分析施加非对称、对称顶推力对连续刚构桥的受力改善作用进行探究，为该类桥实施合龙顶推施工提供参考。

1 顶推位移与顶推力计算

1.1 工程概况

新建兴保地方铁路安家山河预应力混凝土连续刚构桥跨径组合为(81+130+81)m，箱梁截面形式为单箱双室，梁高沿纵向按二次抛物线变化，中支点梁高9.2 m，边支点与中跨跨中梁高4.8 m。5#墩为矩形空心截面独柱墩，墩高85 m；6#墩为双肢实体墩，墩高32 m。主梁采用C55混凝土，5#墩采用C40混凝土，6#墩采用C55混凝土。总体布置如图1所示。该桥上部结构分别从5#墩、6#墩墩顶0#块采用挂篮悬臂对称浇筑施工，中跨侧共有16个悬臂施工节段，分别为4个3 m、5个3.5 m、7个4 m；边跨共计19个悬臂施工节段，分别为4个3 m、5个3.5 m、9个4 m、1个3 m，边、中跨有3个不平衡施工节段。边跨现浇段长度为3.85 m，边、中跨合龙段均为2 m，先中跨合龙，后边跨合龙。

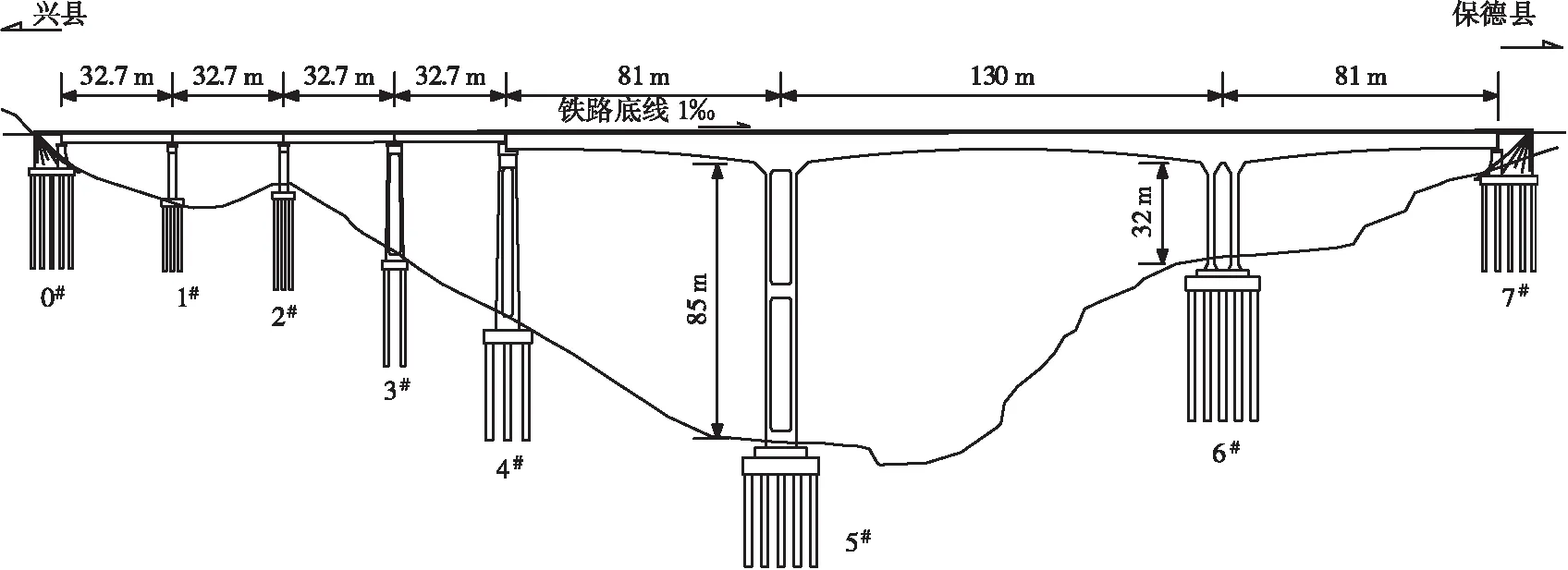
图1 连续刚构桥总体布置图(单位： m)

1.2 有限元模型

主梁、桥墩采用梁单元模拟，模型中共有138个节点，134个单元。墩梁结合处采用弹性连接中的刚接模拟，两边跨采用铰接模拟，仅限制竖向位移，墩底采用固结模拟。建立有限元模型如图2所示。

图2 有限元模型

1.3 确定顶推位移

合龙口水平顶推位移量δd共由3部分组成： ①成桥状态边、中跨不平衡荷载引起的墩顶水平变形δ1；②成桥10 a内的主梁徐变变形引起的墩顶水平偏位值δ2，计算δ2时，一般不考虑边墩支座的水平约束作用，因此对δ2长期徐变作用效应进行折减，按70%与60%乘积取值[11]；③温降引起主梁收缩产生墩顶水平变形δ3。顶推位移量计算见式(1)：

δd=-(δ1+δ2×70%×60%+δ3)

(1)

a.成桥状态边、中跨不平衡荷载引起的墩顶水平变形δ1。考虑桥梁建成后，上部结构自重、预应力张拉力、二期铺装等荷载在边、中跨不平衡引起主墩产生水平位移。

b.混凝土主梁收缩徐变引起主墩偏位δ2。上部结构混凝土主梁收缩徐变往往会引起主梁边、中跨跨中发生较大的竖向挠度，进而导致主墩发生永久水平变位。混凝土收缩徐变通常在成桥后10 a左右趋于稳定，考虑混凝土主梁10 a收缩徐变引起主墩偏位。

c.主梁合龙温差引起的墩顶水平位移δ3。主梁合龙温差是指主桥主跨合龙时的实际温度与设计基准合龙温度之间的差值，当实际合龙温度高于设计基准温度时，当发生温降，主梁紧缩致使主墩产生水平变位，对主梁受力极为不利。根据设计图纸，该桥主桥设计合龙温度为10 ℃进行，实际合龙温度大致处于20 ℃左右，合龙温差ΔT为-10 ℃。根据合龙温差，通过有限元法计算温降10 ℃后主墩产生的水平位移。图3出示了顶推位移与合龙温差的关系曲线。

图3 成桥后温度变化ΔT引起的墩顶水平位移

对图3的2条线进行拟合得到，5#墩墩顶位移与合龙温差的关系为δ3=-0.677 1ΔT；6#墩墩顶位移与合龙温差的关系为δ3=0.554 3ΔT。该桥中跨实际合龙温差约为10 ℃，计算得56#和6#墩墩顶水平位移。

d.顶推位移δd确定。

根据式(1)计算得到5#、6#墩墩顶位移δ1、δ2、δ3和相对位移δd如表1所示。

表1 顶推位移Table 1 Push displacementmm墩号δ1δ2δ3δd5#3.8915.066.77-16.996#-25.06-13.06-5.5436.31

2 顶推力的解析计算法

顶推力解析计算法的思路是利用结构力学力法的平衡方程求解。图4为中跨合龙顶推力计算简化示意图，依次推导5#墩与6#墩在水平力P作用下的水平位移与跨中主梁的竖向位移。忽略主梁在顶推力P作用下的压缩量，将0#块箱梁的惯性矩近似地视为无穷大，即E2I2→∞，E2I4→∞。实际顶推施工时，合龙段顶推力施加于主梁顶面，但先前假设5#墩与6#墩墩顶上部0#块刚度无穷大，顶推力作用下0#块不产生弯矩和位移，则实际发生弯曲变形部位在5#墩与6#墩墩高范围内。因此在图5所示的力学计算见图中，将顶推力P直接作用在A点和B点，其中A点和B点分别为5#墩和6#墩0#块底面与主墩中心线的交接处。

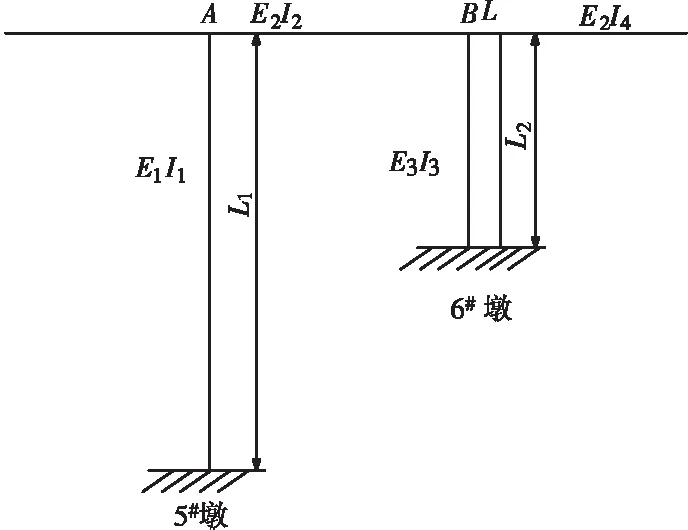
图4 计算简化图

图5 力学计算简图

根据虚功原理分析可知，5#墩的水平位移为：

(2)

6#墩为3次超静定结构，根据图5(b)所示结构简图，力法典型方程见式(3)：

δ11X1+δ12X2+δ13X3+Δ1p=0

δ21X1+δ22X2+δ23X3+Δ2p=0

δ31X1+δ32X2+δ33X3+Δ3p=0

(3)

图乘法可得，6#墩顶推力与顶推位移的关系：

(4)

故总的水平顶推位移Δ56=Δ5h+Δ6h，可简化为：

(5)

其中,E1为5#墩混凝土的弹性模量，取3.4×104MPa；E2为主梁混凝土的弹性模量，取3.6×104MPa；E3为6#墩混凝土的弹性模量，取3.6×104MPa；L1、L2为5#墩和6#墩的墩高；L3为双薄壁墩中心线间的距离；I1、I3为5#和6#墩的惯性矩；I2、I4为5#和6#墩墩顶0#块的惯性矩；e为顶推力P作用水平线到箱梁形心的偏心矩。

在相同的顶推位移下，利用式(5)计算得到顶推力4 263 kN，由有限元模型计算出的顶推力为4 328 kN，二者偏差为2%。本文提出的顶推位移计算式(5)可适用于该类桥合龙顶推力的计算。与有限元存在误差的原因在于5#墩中存在部分实心截面，导致计算过程中5#墩惯性矩计算存在差异。

3 顶推力施加方案

文献[12]表明非对称高墩大跨连续刚构桥的合龙施工，在进行顶推力施加时两侧所需顶推力差别很大，须分开计算。对称高墩大跨度刚构桥合龙顶推施工中，对于合龙口位移采用合龙口两端墩顶水平位移之和。本文拟采用3种顶推力施加方案，方案1：分开计算两墩顶顶推力；方案2：采用合龙口两端对称顶推力。方案3：合龙口不施加顶推力。方案1中顶推力基于Midas Civil中对墩顶施加强制位移，算出相应反力。方案2基于水平位移解析式(5)与有限元计算结果，采用实际施加顶推力4 000 kN。合龙顶推力施加方案如表2所示。

表2 合龙顶推力施加方案Table 2 Applying scheme of closed top thrustΔ5/mmΔ6/mm(Δ5+Δ6) /mmP/kN方案1-16.990-16.991 839036.3136.3110 908方案2-16.9936.3153.304 000方案30000注: 正值表示向右变形,负值表示向左变形。

4 顶推效果分析

对比分析3种顶推力施加方案在连续刚构桥中跨顶推合龙顶推施工的对主梁线形、受力、桥墩应力的改善作用。分别对比：方案1：施加非对称顶推力合龙；方案2：施加对称顶推力合龙；方案3：未施加顶推直接合龙。其主梁竖向位移变化较大的节点位置示意图如图6所示。

图6 主梁主要节点及桥墩主要截面示意图

4.1 主梁线型

在方案1、2、3作用下，其主梁发生10 a收缩徐变后竖向位移会发生变化，变化趋势如图7所示，在5#墩左侧和中跨合龙口其竖向位移变化较大。中跨合龙口竖向位移方案1、2相比方案1较大，边跨合龙口方案1、2位移基本相同，均大于方案3。位移变化较明显的节点号位于7～15，40～50范围内，分别处于5#墩左侧32.65～64.15 m、5#墩右侧35.85～73.85 m段。取其中几个位移变化值较大的节点进行对比分析，如表3所示。

图7 10 a收缩徐变作用下主梁累计竖向位移

表3 主梁关键节点竖向位移Table 3 Vertical displacement of key nodes of main beam节点竖向位移/mm方案1方案2方案37-126.3-135.6-89.68-123.6-132.4-89.29-114.0-122.1-81.810-103.4-111.0-73.611-91.7-98.6-64.112-81.8-88.2-56.513-73.2-79.0-50.24122.332.43.04227.339.06.54331.645.29.74434.550.111.44538.856.514.74643.263.218.24753.475.827.5

如表3所示，由于墩身的高度差异和悬臂段长度不一致，导致主梁竖向挠度呈现出不对称性。在长期收缩徐变下，主梁中跨区间，方案1、2作用产生的挠度绝对值明显大于方案3。其中中跨顶推位置47号节点竖向挠度，方案1、2分别为53.4、75.8 mm，方案3为27.05 mm，即施加顶推力会使得中跨合龙位置具有较大的上拱值，从而避免中跨位置低于桥梁轴线。由于非对称墩高和桥墩形式不同导致桥墩刚度不一致，对称顶推力作用，5#墩的变形能力更大，导致合龙口两端位移不一致，非对称顶推力作用下，主梁合龙口竖向高度一致。从对中跨下挠作用的控制而言，施加对称顶推力比施加非对称顶推力控制作用更加明显。

4.2 桥墩应力

连续刚构桥通过顶推施工后中跨合龙，从静定结构变为超静定结构，完成体系转换。为探究施加对称、非对称顶推力对桥墩应力的改善作用，方案1、2、3顶推作用下桥墩墩顶与墩底应力在顶推阶段、中跨合龙、二期铺装、收缩徐变10 a各阶段的变化如图8～图10所示。

图8 方案1桥墩应力

图9 方案2桥墩应力

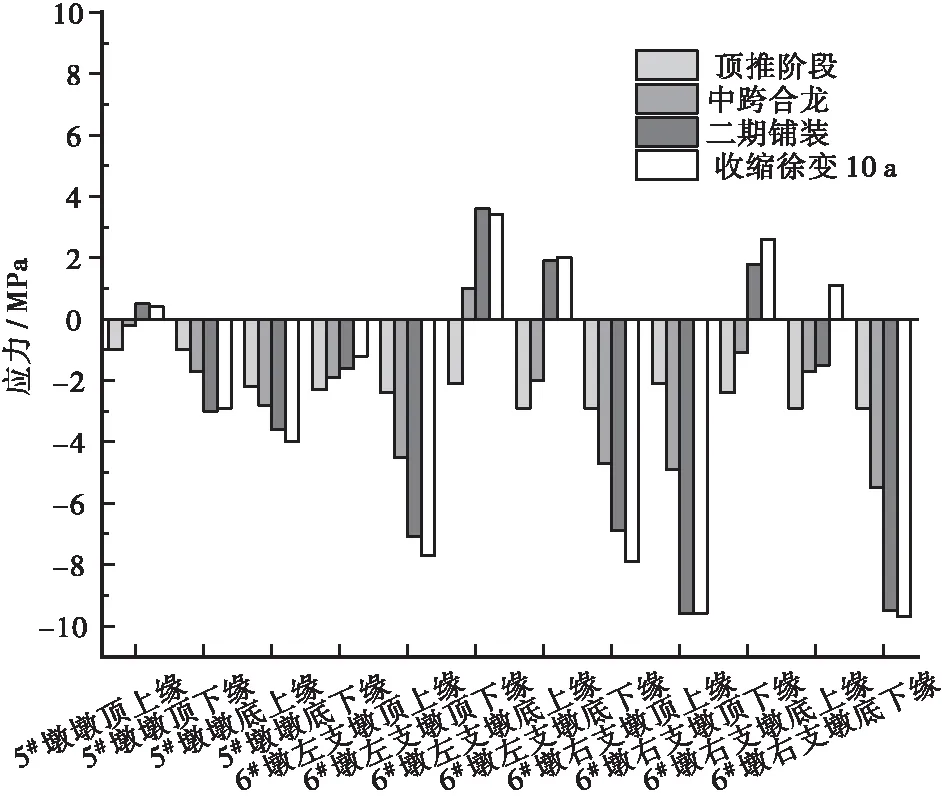
图10 方案3桥墩应力

由图8可知，当对合龙口施加非对称合龙顶推力时，5#墩在顶推阶段、中跨合龙、二期铺装、收缩徐变10 a 这4个阶段均处于较低应力状态。6#墩在顶推阶段，左右支墩顶上缘、墩底下缘均处于受拉状态，最大拉应力为5.9 MPa；中跨合龙阶段，6#墩左右支墩顶出现拉应力，最大为2.5 MPa；收缩徐变10 a后，6#墩左支墩顶下缘拉应力为2.1 MPa。

由图9可知，对合龙口施加对称顶推力，在顶推阶段，除6#墩左支墩顶上缘出现0.7 MPa拉应力，其他位置均处于受压状态。中跨合龙阶段桥墩均处于受压状态。二期铺装阶段，5#墩、6#墩左支墩顶上缘均处受拉状态，6#墩左支墩顶下缘拉应力为1.9 MPa。在收缩徐变10 a后，5#墩墩顶上缘、6#墩左右支墩顶下缘、6#墩左支墩底上缘、均出现拉应力，其中6#墩左支墩顶下缘拉应力最大，为2.1 MPa。

由图10可知，合龙口未施加顶推力，顶推阶段，桥墩处于受压状态。中跨合龙阶段，6#墩左支墩顶下缘存在1 MPa的拉应力，其他截面均处于受压状态。二期铺装阶段，5#墩墩顶上缘、6#墩左右支墩顶下缘、6#墩左支墩底上缘、均处受拉状态，其中6#墩左支墩顶下缘拉应力为3.6 MPa。收缩徐变10 a后，5#墩墩顶上缘、6#墩左右支墩顶下缘、6#墩左右支墩底上缘均出现拉应力，其中6#墩左支墩顶下缘表面拉应力为3.4 MPa。

总体而言，合龙口施加非对称顶推力和未施加顶推，进行中跨合龙和之后各个阶段，桥墩部分位置将出现较大的拉应力，导致桥墩表面存在开裂风险。合龙口施加对称顶推力，在中跨合龙和之后阶段，桥墩部分位置依旧会处于受拉状态，但拉应力均处于合理范围，降低桥墩表面出现开裂风险。因此，合龙口施加对称顶推力对桥墩受力的改善优于施加非对称顶推力。

4.3 主梁应力

顶推前后主梁应力会有所变化，在考虑施工阶段自重，预应力和混凝土收缩徐变等荷载组合作用下，方案1、方案2、方案3下主梁顶板与底板最大、最小应力值如表4所示。

表4 主梁应力对比Table 4 Comparison of main beam stress应力最值应力/MPa方案1方案2方案3顶板Max-1.3-1.3-1.3顶推后Min-13.3-13-12.8底板Max0.60.40.3Min-6.9-6.9-6.9顶板Max-1.3-1.3-1.3中跨合龙Min-14.6-14.2-14底板Max0.30.30.3Min-10.9-10.6-10.6顶板Max000二期成桥Min-13.9-13.5-13.3底板Max000Min-11.7-11.7-11.7顶板Max000Min-12.4-12.6-12.5收缩徐变10 a底板Max000Min-11.5-11.6-11.6

由表4可知，施加非对称顶推力及对称顶推力对其顶推过程、中跨合龙、二期成桥过程的主梁应力变化不大，桥梁10 a收缩徐变后，其主梁应力没有太大变化。即施加顶推对主梁应力变化基本没有影响。

5 结论

a. 推导出的空心箱型墩和双肢实心墩其顶推力和顶推关系之间的解析公式，计算简单，经验证有较高的精度可用于该类结构合龙顶推力的计算。

b.合龙口施加非对称顶推力和未施加顶推，进行中跨合龙和之后各个阶段，桥墩部分位置将出现较大的拉应力，导致桥墩表面存在开裂风险。合龙口施加对称顶推力，在中跨合龙和之后阶段，桥墩部分位置依旧会处于受拉状态，但拉应力均处于合理范围，降低桥墩表面出现开裂风险。

c.对于非对称高墩连续刚构桥的顶推施工中，宜采用对称顶推力进行顶推，对于主梁线形、桥墩受力状态存在明显改善。