毗邻边坡连续刚构梁桥地震位移和加速度分析
2022-04-04焦志鹏喻泽红
焦志鹏,喻泽红
(中南大学 土木工程学院,湖南 长沙 410076)
我国西南地区的公路和铁路工程中,线路高差大,起伏明显,弯桥和坡桥较多,为避免高差引起的桥梁 “爬移”现象,一般将桥梁结构中墩较高、刚度相差不大的桥墩与主梁固结,形成刚构体系,利用墩体自身柔性适应上部结构的变形。
与连续梁结构体系相比,刚构体系需承担不同的水平力作用,包括横坡滑坡、变形、地基失效、收缩徐变、温变和制动力等[1-2],在地震中,这些作用往往会放大地震作用,加剧结构破坏。Wenchuan(2008); Tohoku Pacific Earthquake(2011)等地震灾害调查表明,在横向陡坡处,存在较多的桥基塌滑、落梁、桥柱弯曲破坏、桥柱连梁破坏、桥梁横向变位过大,横桥挡块破坏等情况。由于较大的水平地震力,桥梁下部结构瞬时反复振动,在相对薄弱的截面破坏,引起桥梁倒塌,其中高墩以弯曲型破坏为主,表现为混凝土开裂、压溃和主筋弯曲和箍筋松脱等,粗矮墩刚性大,以脆性折断的剪切破坏为主[1-4]。由于特定的结构形式和特殊的场地条件,毗邻山坡连续刚构梁桥体系的地震反应有不同的特点,系统研究其地震位移和加速度反应,并与现有桥梁地震破坏资料对比,对此类桥梁的抗震设计加固很有实际意义[5-6]。
在桥梁抗震相关研究中,桩土地震反应特性的试验和理论研究一直很活跃,较多侧重对p-y曲线的验证与修正,ASHLOCK[7]等、ROLLINS[8]等、朱斌[9]等、MANNAL[10]等、CHRISTOPHER[11]等都有丰硕成果,但没有考虑边坡的影响,他们也认为需要进一步研究。相对水平场地,毗邻边坡或坡体中的桩基,桩土反应特性不同,一些学者着重研究了桩在坡体中位置、深度、边坡坡度、潜在滑裂面位置、土体类型、桩径和桩体材料等因素对桩土反应的影响,MIRZOYAN[12]等和NIMITYONGSKUL[13]等研究桩与坡顶距离对桩土反应的影响,认为当桩与坡顶距离大于桩径4倍后,边坡影响减小,8倍时消失。赵明华[14]等试验研究横坡段桩柱式桥梁双桩基础破坏模式和承载机理,分析横坡段桩柱的内力分布规律,是该领域较新研究报道。
边坡-桩基-梁体作用体系的地震反应特性,不仅与边坡和桩基作用特性相关,还与上部梁体结构与桩柱间力传递特性,以及坡面以上柱桩结构自身几何特性和材料特性有关。类似作用体系的研究,较早集中于高桩码头结构体系中。魏汝龙[15]和王年香[16]等进行了高桩码头-岸坡体系离心模型试验,并与有限元分析结果对比,提出针对性的高桩码头-边坡体系设计方案。JEREMIC[17]等对Oakland港口码头结构进行地震反应分析,认为考虑结构与岸坡作用对结构抗震设计的利弊决定于岸坡-桩基-上部结构体系的地震特性;LU[18]等研究Los Angeles港桩基-上部结构-岸坡体系地震特性,认为对码头-桩基-岸坡进行整体分析更合理。GIANNAKOU[19]等采用三维有限元模型进行了类似研究。梁雨兰[20]等着重研究了桩基布置型式对高桩码头结构与岸坡作用体系地震反应特性的影响,计算了高桩弯矩内力。SHAMSABADI[21]和CAKIR[22]等考虑结构与土体作用,研究地震频率对结构反应的影响,计算了地震位移。 ERHAN[23]等选用大、中、小震的3种地震波对桥梁结构整体分析,认为大震和中震作用下,考虑桥梁结构与土相互作用,计算结果更为合理。
这些研究从不同侧面不断丰富了该领域研究内涵,本文在总结分析已有研究方法和研究成果基础上,考虑边坡土体与桩基的作用,建立毗邻边坡刚构连续梁桥体系三维有限元分析模型,计算分析体系的振动特性以及地震反应,并与文献记录的桥梁结构实际地震破坏性状和特征比较分析,验证方法合理性,对结构主要特征位置的地震位移和加速度反应进行分析,研究对于山区连续刚构梁桥抗震加固设计有借鉴意义。
1 计算方法
1.1 计算模型
以毗邻边坡一连续刚构桥梁其中五跨建立三维动力有限元计算模型,跨长8 m,墩体横距4 m,桩径1 m,半结构平面布置见图1(a)。边坡上、下部为平台,宽度10 m,坡底距模型底部20 m,坡度45°,坐标系x轴,y轴分别垂直和平行于边坡竖面,z轴为竖直方向,见图1(b)。
本文论述中,边坡上侧、中部和下侧的桩体位置分别对应图中A1、B1和C1、A2、B2和C2、A3、B3和C3相应位置;边桩、次边桩、中间桩位置分别对应C1、C2、C3,B1、B2、B3和A1、A2、A3相应位置,见结构半平面布置图1(a)。
纵梁指沿桥梁纵向的梁体,其中边坡上侧的纵梁包括CLC1、ZLB1和ZLA1,边坡下侧的纵梁为CLC3、ZLB3和ZLA3,边坡中部纵梁包括CLC2、ZLB2和ZLC2;边跨中远离计算对称面的横梁依次为边跨横梁、次边跨横梁和中跨横梁。
考虑模型计算幅度对计算结果的影响,试算后,确定土体计算幅度60 m×60 m×100 m,远大于桩基和梁体结构几何尺寸。土体边界为人工截断边界,模型底部固定,土体横向和纵向边界节点竖向约束。模型单元采用8节点3D实体单元,土体采用SOLID45,桩基础和梁体采用SOLID65。刚性目标面采用TARGE170单元,柔性接触面采用CONTAL173单元,接触单元对间利用单元实常数识别。网格划分采用自定义尺寸,桩周土体网格加密,生成25 633个单元,模型和单元网格见图1(b)[24-26]。

(a)结构平面布置
1.2 模型材料
桩体和上部梁体为弹性材料,模量2.5 E10 Pa,密度2.5×103kg/m3,泊松比0.2,土体为DP材料,弹性模量2.5 E8 Pa,密度2.0×103kg/m3,泊松比0.4。为考虑桩土间不同界面设置对计算结果的影响,计算模型设置2种界面类型,见表1。

表1 桩土界面设置条件Table 1 Soil-pile interface模型类别桩-土界面设置类型荷载类型1桩-土间固结结构自重2桩-土间设置1类接触结构自重3桩-土间设置1类接触地震荷载
1.3 地震波的输入
选用EI-Centrol地震波输入,加速度峰值3.417 m/s2,荷载步0.01 s,阶跃式加载。考虑到土体材料和界面接触非线性,计算收敛困难,用一致输入法输入水平横向地震波。时程分析前,关闭时间积分效应,进行重力荷载作用分析,求解完成后,打开时间积分效应,输入地震荷载进行时程分析。采用瑞雷阻尼计算,对许多结构工程计算,其精度可以满足要求[24-26]。
1.4 计算模型的间接验证
文献[1-4]分析了Wenchuan(2008)和Tohoku Pacific Earthquake(2011)等地震中,类似结构体系地震破坏的主要性状和特征,其中坡体中桥梁结构的破坏较多表现为落梁、桥柱弯曲破坏、桥柱连结破坏、桥梁结构横向变位过大等。由于现有资料和动力计算方法的局限性,本文的计算模型虽然无法完全模拟地震中桥梁的真实地震反应,但计算得到的桩体、墩体和梁体结构的地震位移和加速度反应中,桥梁结构地震反应较大的位置与地震破坏主要性状较吻合,一定程度上证实了本文计算模型和方法的合理性。
2 毗邻边坡连续钢构梁桥体系自振特性分析
自振频率和周期是结构体系振动特征值,桩土界面设置对计算结果影响较大,本文通过设置不同界面计算分析其对体系振动特性的影响,文中仅论述前六阶振型和自振周期,具体分析详见文献[26]。
2.1 不同桩土界面设置对结构体系自振频率和周期的影响
表2为毗邻边坡连续梁桥体系前六阶模态扩展运算结果。计算表明,考虑桩土间接触作用后,自振频率出现小幅度降低,自振周期延长,其中,第五阶振型自振周期增幅达到6.91%,主要由于桩土界面采用接触设置时桩土间约束相对较小,体系柔性增加,刚度下降。表2同时可看出,界面设置对高阶振型影响相对较大,也同样基于毗邻边坡刚构梁桥各方向的刚度差。
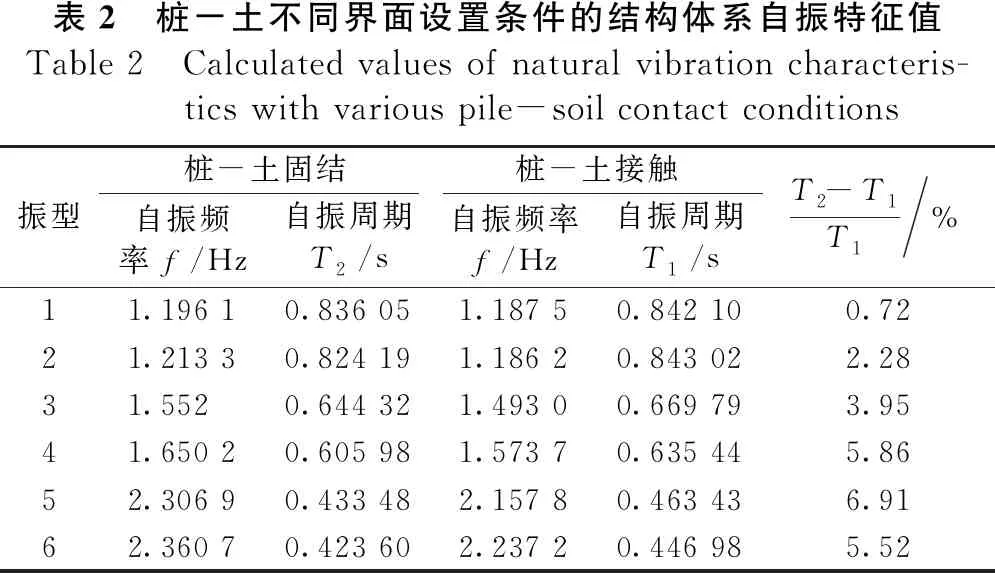
表2 桩-土不同界面设置条件的结构体系自振特征值Table 2 Calculated values of natural vibration characteris-tics with various pile-soil contact conditions振型桩-土固结桩-土接触自振频率f/Hz自振周期T2/s自振频率f/Hz自振周期T1/sT2-T1T1%11.196 10.836 051.187 50.842 100.7221.213 30.824 191.186 20.843 022.2831.5520.644 321.493 00.669 793.9541.650 20.605 981.573 70.635 445.8652.306 90.433 482.157 80.463 436.9162.360 70.423 602.237 20.446 985.52
2.2 不同桩土界面设置对结构体系振型的影响
桩-土间接触模型模态分析中,仅显示桩体和梁体,没有土体单元。总体上,在边坡-桩基-梁体作用体系中,由于土体对下部桩体位移的约束,位于坡体内的桩体弯曲程度较小,主要表现为桥墩弯曲。
如图2所示,第一阶振型中,桩体和梁体没有明显弯曲,上部结构向边桩方向倾斜;第二阶振型中,边桩桥墩纵向弯曲,此振型为桥墩沿桥梁纵向振动的主振型;第三振型中,梁体明显弯曲,靠端桩和边坡上侧的纵梁向下凹陷,另一方向上,边坡上侧纵梁向上微凸,呈反对称竖向弯曲;第四阶振型中,桩体弯曲不明显,梁体呈正对称变形,说明此振型为纵梁竖向振动的主振型;第五阶振型中,只有边桩桥墩沿负向纵向弯曲;第六阶振型表现为桩体沿纵向,梁体沿竖向复合振型,其中桩体纵向弯曲,边坡上侧纵梁下凹,边坡下侧的纵梁上凸。

(a)第一阶振型(T=0.842 1 s)
3 桩基和梁体地震位移与加速度反应分析
结合振型分析,本文分别计算不同位置的桩基和梁体不同特征点地震位移与加速度时程,包括桩基中点、顶点,以及上部纵、横梁跨中等横向、竖向和纵向位移与加速度时程曲线,为节约篇幅,仅提供部分时程曲线,具体分析参见文献[26]。本文主要提取各特征点地震反应最值进行分析。
图3为次边桩桩顶地震位移时程曲线,桩顶横向位移经过波动后达到最大值,然后小幅震荡。在1.8~2.2 s位移增幅较大,继而降低再增大,随地震时程,边坡上侧、中部和下侧桩顶横向位移分别在9、6和3 cm左右小幅波动。从桩顶竖向位移看,施加初始荷载步,竖向位移已达最大值,由于桥梁竖向位移主要由静力决定,承受地震荷载时竖向位移波动幅度不大,这与历次地震中,较少出现因桩基竖向位移过大导致桥梁地震坡坏情况相符。

(a) 横向
图4为次边桩桩顶地震加速度时程,横向加速度在初始3 s内,振动幅值达到最大值9.419 m/s2,与其它加速度时程曲线相比,某些时间点边坡下侧桩体的横向加速度幅值较高;从次边桩桩顶竖向加速度时程看,边坡上侧桩体加速度振动幅值大于其余二者。在纵向加速度时程曲线中,边坡上侧桩体前3 s中加速度幅值明显大于中部与边坡下侧桩体,在后续时间点,边坡下侧的桩顶纵向加速度较大。

(a) 横向
从横、竖向和纵向3个方向加速度对比看,竖向和纵向加速度振幅在±5 m/s2间,横向加速度振幅在±10 m/s2间。从相位看,3根桩体3个方向地震加速度反应存在相位差,各桩桩顶加速度波峰或波谷并不互相对应,由于计算数据量大,时间间隔小,图示不够明显,具体见文献[26]。
3.1 桩基和梁体地震位移反应分析
3.1.1桩基地震位移
表3为边坡上侧桩体桩顶和桩中各位移时程曲线中位移最大和最小值,除个别位置外,桩体横向位移的最值均比纵向和竖向位移最值大。边桩桩中竖向和纵向位移仅为其横向位移的12%和6.6%左右;边桩桩顶竖向位移和纵向位移为其横向位移的8.5%和17%左右;中间桩横向位移与纵向位移和竖向位移间相差较小,中间桩顶竖向位移和纵向位移为其横向位移的13.2%和27.6%左右。总体上,桩顶位移值大于桩中位移,边桩桩中横向位移最大值为61.9 cm,桩顶横向位移最大值为119 cm,相差47%左右;中间桩桩中横向位移最大值5.84 cm,桩顶横向位移最大值77.7 cm,相差90.2%左右;次边桩相差61.2%。从位移绝对值看,中间桩位移比其它桩相应位置的桩相对较小,边桩位移值最大,中间桩桩顶横向和竖向位移仅为边桩的65%和55%左右,主要由于其相应位置受坡体和结构体系约束相对较多。
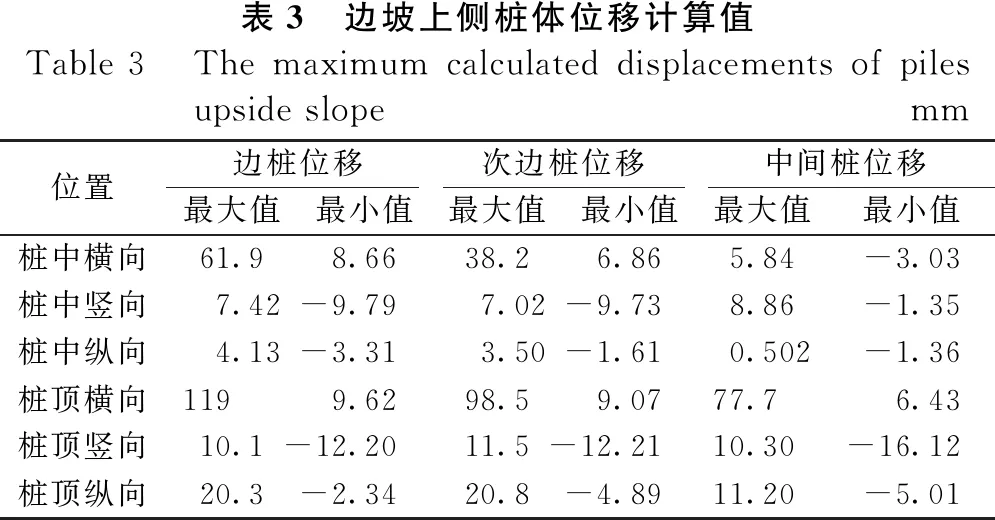
表3 边坡上侧桩体位移计算值Table 3 The maximum calculated displacements of piles upside slopemm位置边桩位移次边桩位移中间桩位移最大值最小值最大值最小值最大值最小值桩中横向61.98.6638.26.865.84-3.03桩中竖向7.42-9.797.02-9.738.86-1.35桩中纵向4.13-3.313.50-1.610.502-1.36桩顶横向1199.6298.59.0777.76.43桩顶竖向10.1-12.2011.5-12.2110.30-16.12桩顶纵向20.3-2.3420.8-4.8911.20-5.01
表4为边坡中部桩体桩顶和桩中各位移时程曲线中位移最大和最小值,地震作用下,边坡中部桩体桩顶位移均大于桩中位置对应方向的位移,横向位移表现相对明显,次边桩桩顶与桩中横向位移相差83.56%,由于边坡土体约束,桩中位移在毫米级范围波动,而桩顶位移在厘米级波动。从绝对值看,边坡中部桩体中,边桩位移最大,次边桩稍小,中间桩最小。与表3相比,边坡上侧桩体位移明显大于边坡中部桩体位移,对于边桩,边坡中部桩体桩顶和桩中横向位移分别为边坡上侧的79.3%和60.7%左右。但与此同时,中间桩位移最值变化相对较小,边坡中部中间桩桩顶和桩中横向位移与边坡上侧中间桩相差3%和17%左右。
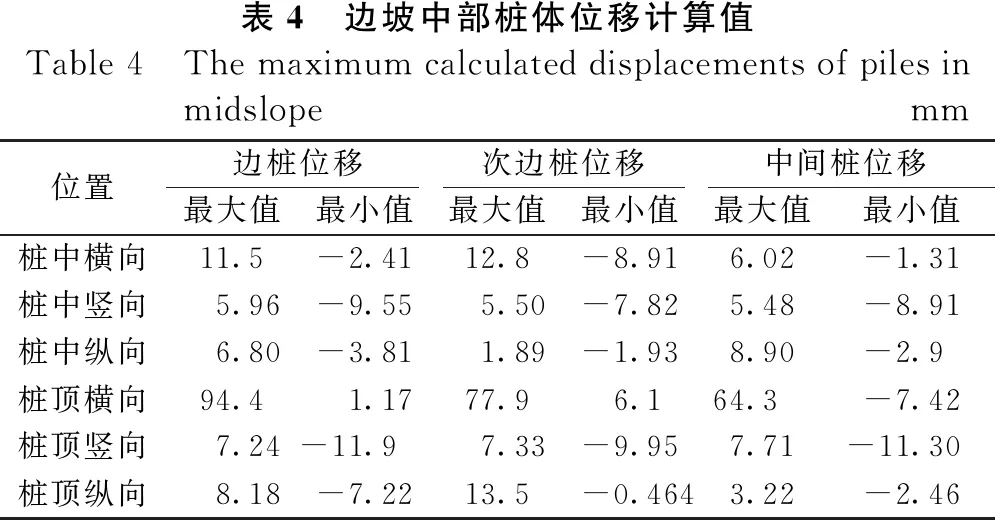
表4 边坡中部桩体位移计算值Table 4 The maximum calculated displacements of piles in midslopemm位置边桩位移次边桩位移中间桩位移最大值最小值最大值最小值最大值最小值桩中横向11.5-2.4112.8-8.916.02-1.31桩中竖向5.96-9.555.50-7.825.48-8.91桩中纵向6.80-3.811.89-1.938.90-2.9桩顶横向94.41.1777.96.164.3-7.42桩顶竖向7.24-11.97.33-9.957.71-11.30桩顶纵向8.18-7.2213.5-0.4643.22-2.46
表5为边坡下侧桩体桩顶和桩中各位移时程曲线中位移最大和最小值,整体看,边坡下侧桩体位移最大值为边桩桩顶的横向位移58.6 cm。除中间桩与次边桩的桩顶横向位移外,其余位置各个方向的位移最小值为负值,说明地震作用下,某些时间点,桩体发生了沿坐标轴负向的位移。所有桩体位移最大值均为正值,桩顶位移普遍大于桩中相应方向的位移,中间桩的位移值普遍小于次边桩相应方向的位移,相比而言,边桩位移值最大,对于横向位移,中间桩桩中和桩顶位移分别为次边桩和边桩的55%、51.6%和90%、70.8%。相比表3和表4,表4与表5中位移最大值相差幅度减小,其中桩中横向位移分别变化26%,17.9%,3.8%,而表3与表4中位移最大值相应变化的81.4%,66.5%,3.1%。总体上,中间桩地震反应相对较小。
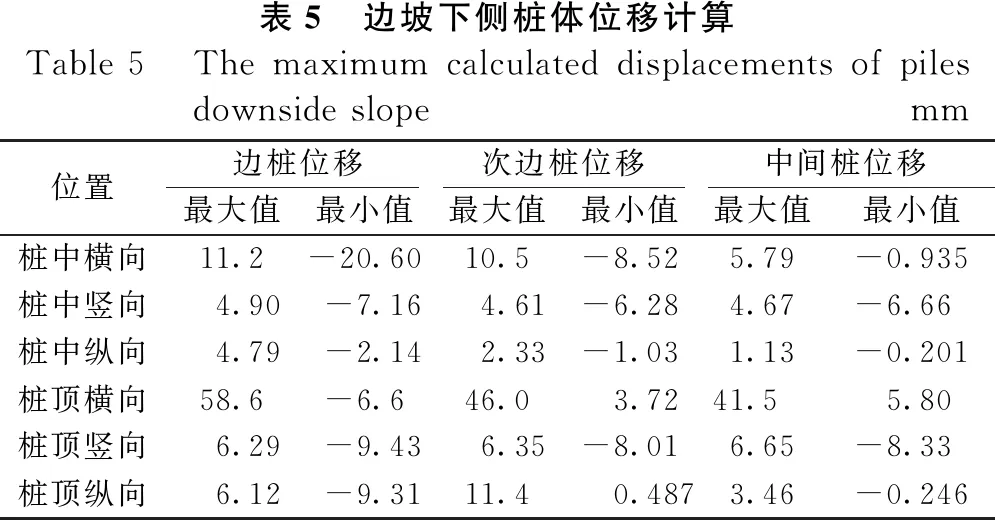
表5 边坡下侧桩体位移计算Table 5 The maximum calculated displacements of piles downside slopemm位置边桩位移次边桩位移中间桩位移最大值最小值最大值最小值最大值最小值桩中横向11.2-20.6010.5-8.525.79-0.935桩中竖向4.90-7.164.61-6.284.67-6.66桩中纵向4.79-2.142.33-1.031.13-0.201桩顶横向58.6-6.646.03.7241.55.80桩顶竖向6.29-9.436.35-8.016.65-8.33桩顶纵向6.12-9.3111.40.4873.46-0.246
3.1.2上部梁体地震位移
表6为纵梁跨中位移最大、最小计算值,各个位置的位移最大值为跨中横向位移,其中以边跨纵梁位移最大10.7 cm,竖向和纵向的位移最值相对较小,约为横向位移的10%~20%;对于同跨但在坡体中位置不同的3根纵梁,跨中横向位移差别也很小,说明横向地震波作用下,纵梁以横向位移反应为主,也不存在梁体沿坐标轴负向的位移。对于竖向和纵向位移,纵梁位移最小值为负值,即发生沿坐标轴负向的位移。同时,边跨纵梁竖向和纵向位移低于中间跨纵梁,在边坡上侧纵梁中,边跨纵梁分别仅为中间跨纵梁的65.5%和96.2%。对于横向位移,边跨纵梁的横向位移最值均大于次边跨和中间跨纵梁,但竖向和纵向位移最小值的绝对值与此不同。
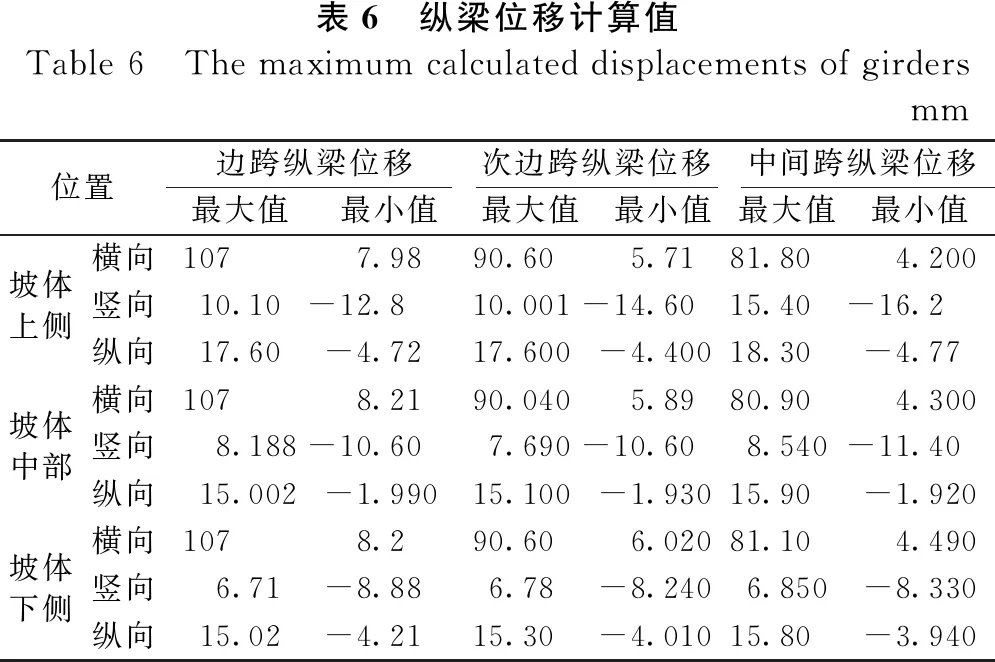
表6 纵梁位移计算值Table 6 The maximum calculated displacements of girdersmm位置边跨纵梁位移次边跨纵梁位移中间跨纵梁位移最大值最小值最大值最小值最大值最小值横向107 7.9890.60 5.7181.80 4.200坡体上侧竖向10.10-12.810.001-14.6015.40-16.2纵向17.60-4.7217.600-4.40018.30-4.77横向1078.2190.0405.8980.904.300坡体中部竖向8.188-10.607.690-10.608.540-11.40纵向15.002-1.99015.100-1.93015.90-1.920横向1078.290.606.02081.104.490坡体下侧竖向6.71-8.886.78-8.2406.850-8.330纵向15.02-4.2115.30-4.01015.80-3.940
表7为横梁跨中位移最大、最小计算值,边跨中边坡上、下侧横梁的横向和纵向位移最大值相差不大,横向位移相差1 mm,纵向位移相差0.3 mm。对于竖向位移,边坡上侧横梁的竖向位移最大值稍大于边坡下侧横梁的跨中竖向位移,边跨、次边跨和中间跨跨中分别相差2.11、1.65和1.7 mm。与相应位置纵梁相比,边跨和次边跨横梁横向位移大约高出1个厘米级,中间跨表现不明显。边跨横梁位移的最小值中,上侧横梁位移最小值的绝对值高于边坡下侧对应方向的位移。次边跨横梁与中间跨横梁竖向位移向较接近,但边跨横梁的跨中横向位移相对较大,约高出次边跨和中间跨2~3 cm。
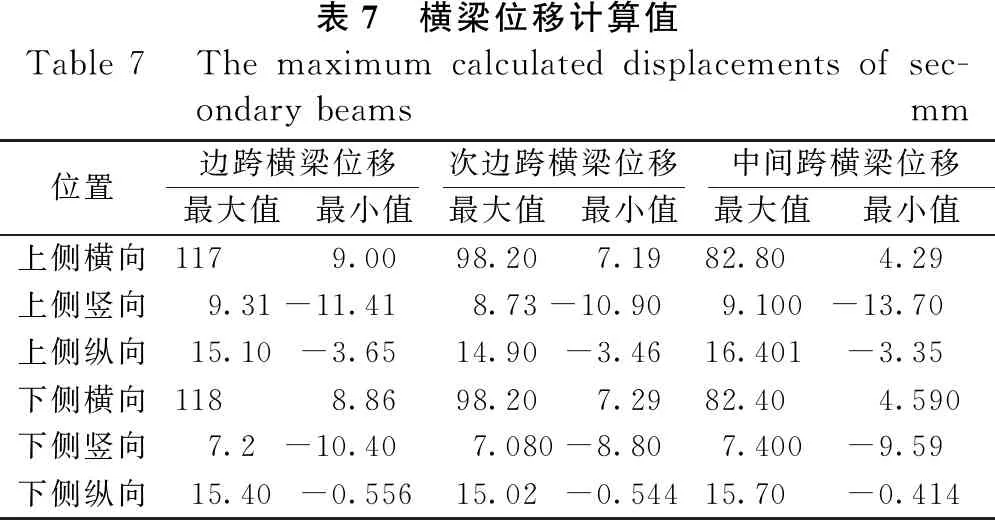
表7 横梁位移计算值Table 7 The maximum calculated displacements of sec-ondary beamsmm位置边跨横梁位移次边跨横梁位移中间跨横梁位移最大值最小值最大值最小值最大值最小值上侧横向117 9.0098.207.1982.80 4.29上侧竖向9.31-11.418.73-10.909.100-13.70上侧纵向15.10-3.6514.90-3.4616.401-3.35下侧横向1188.8698.207.2982.404.590下侧竖向7.2-10.407.080-8.807.400-9.59下侧纵向15.40-0.55615.02-0.54415.70-0.414
3.2 桩基和梁体地震加速度反应分析
3.2.1桩体加速度
表8为边坡上侧桩体计算加速度最大、最小值,总体上桩顶加速度绝对值比桩中大一些,边坡上侧次边桩中,桩中横向和竖向加速度分别为桩顶的78.9%和67.6%,但桩顶纵向加速度比桩中稍小,在边坡上侧边桩和次边桩中,桩顶纵向加速度分别为桩中纵向加速的80%和95%。而中间桩的桩顶纵向加速度大约为桩中纵向加速度的2倍左右。

表8 边坡上侧桩体加速度计算值Table 8 The maximum calculated accelerations of piles upside slope m/s2位置边桩加速度次边桩加速度中间桩加速度最大值最小值最大值最小值最大值最小值桩中横向8.726-4.0267.441-4.169 42.455-1.852 桩中竖向4.986-1.9764.282-4.029 40.780-0.836桩中纵向6.799-8.4035.107-1.751 21.381-1.229桩顶横向9.949-7.2959.419-5.1633.515-3.294桩顶竖向8.340-4.6826.333-4.984 11.239-1.094桩顶纵向5.443-9.1594.872-7.498 32.966-3.252
表9为边坡中部桩体计算加速度最大、最小值,边桩桩顶各个方向的加速度绝对值大于桩中加速度值,其中竖向加速度变化相对明显,桩顶竖向加速度约为桩中的3倍左右。对于次边桩加速度最大值,桩中横向和纵向加速度比桩顶加速度略高,分别相差0.85和1.20 m/s2,但桩顶纵向加速度明显高于桩中纵向,相差2.20 m/s2。对于中间桩,桩顶横向和竖向加速度比桩中高,但中间桩的桩顶纵向加速度最大值低于桩中纵向加速度,最小值绝对值又略微高些。

表9 边坡中部桩体加速度计算值Table 9 The maximum calculated accelerations of piles in midslopem/s2位置边桩加速度次边桩加速度中间桩加速度最大值最小值最大值最小值最大值最小值桩中横向6.362-7.234 6.142-4.8272.807-2.050 桩中竖向2.961-3.8120.889-0.6640.841-0.665桩中纵向7.326-5.4293.362-2.4291.274-0.543桩顶横向8.321-9.7035.291-4.0043.479-2.835桩顶竖向9.81-6.7713.091-2.8431.184-0.882桩顶纵向8.540-7.6022.164-1.8780.678-0.927
表10为边坡下侧桩体计算加速度最大、最小值,边桩桩顶竖向和纵向加速度比桩中加速度值分别高出2.52和1.49 m/s2,但桩顶横向加速度最大值比桩中略低,最小值相差2.74 m/s2。次边桩的加速度最大值与边桩变化规律类似,但幅度相对较小,其桩顶竖向和纵向加速度比桩中加速度值分别高出0.77和1.19 m/s2,桩顶横向加速度最大值比桩中低0.18 m/s2,最小值相差0.13 m/s2。对于中间桩,桩顶各个方向加速度最大值或最小值的绝对值均高于桩中相应方向的加速度,但相差幅度不大,不超过0.3 m/s2。

表10 边坡下侧桩体加速度计算值Table 10 The maximum calculated accelerations of piles downside slopem/s2位置边桩加速度次边桩加速度中间桩加速度最大值最小值最大值最小值最大值最小值桩中横向8.060-5.2475.569-5.3822.744-2.059 桩中竖向2.346-1.1600.589-0.5740.672-0.727桩中纵向5.010-4.9351.825-1.2650.980-0.453桩顶横向7.606-7.9845.385-5.5113.044-3.171桩顶竖向4.869-4.1431.362-1.0220.813-0.743桩顶纵向6.497-5.0513.022-2.4361.049-1.103
3.2.2上部梁体加速度
表11为边坡上侧、中部和边坡下侧纵梁加速度最大和最小计算值,边坡上侧的纵梁加速度相对较大,边坡中部和下侧的纵梁相对较小,其横、竖、纵3个方向加速度分别相差0.25、2.67和-0.54 m/s2,下侧纵梁与上侧纵梁相差相对较大,分别为0.88、4.13和3.66 m/s2。边坡上侧和下侧的边跨和次边跨纵梁的加速度相差不大,除上侧竖向加速度相差1.05 m/s2外,其余不超过0.5 m/s2,而中部竖向加速度则相差2.24 m/s2。中间跨纵梁各位置的横向加速度与边跨相差3.31 m/s2以上,但纵向加速度相差不超过1.09 m/s2,上、下侧竖向加速度相差不超过0.38 m/s2,而中部竖向加速度相差2.42 m/s2。边坡上侧边跨纵梁竖向加速度11.1 m/s2为纵梁最大加速度值,边坡中部边跨纵梁的纵向加速度6.1 m/s2,以及边坡下侧的中间跨纵梁的横向加速度6.0 m/s2为纵梁较小的加速度值。

表11 纵梁加速度计算值Table 11 The maximum calculated accelerations of girdersm/s2位置边跨纵梁加速度次边跨纵梁加速度中间跨纵梁加速度最大值最小值最大值最小值最大值最小值上侧横向10.19-7.89410.16 -10.01 6.390-4.050上侧竖向11.10-10.6810.050-10.69710.90-10.90上侧纵向10.30-10.0510.72-8.4789.94-8.12中部横向9.568-7.6739.028-9.866.260-4.540中部竖向9.639-9.2707.4-8.0207.219-6.291中部纵向6.10-3.9027.26-3.8227.190-4.14下侧横向9.310-10.788.73-9.6106.000-4.470下侧竖向6.970-8.186.810-7.6506.585-6.262下侧纵向6.640-4.2706.810-4.1406.741-4.130
表12为横梁加速度计算值,次边跨横梁上、下侧横向加速度10.55和10.84 m/s2为加速度较大者,其与边跨横梁和中间跨横梁上、下侧横向加速度分别相差3.28、5.15、3.66和5.5 m/s2。边坡上侧3根横梁的竖向加速度相差不超过1.5 m/s2,下侧相差不超过0.596 m/s2。边坡上侧3根横梁的纵向加速度中,次边跨横梁与边跨和中间跨横梁分别相差3.43和1.42 m/s2,下侧相差不超过0.92 m/s2。
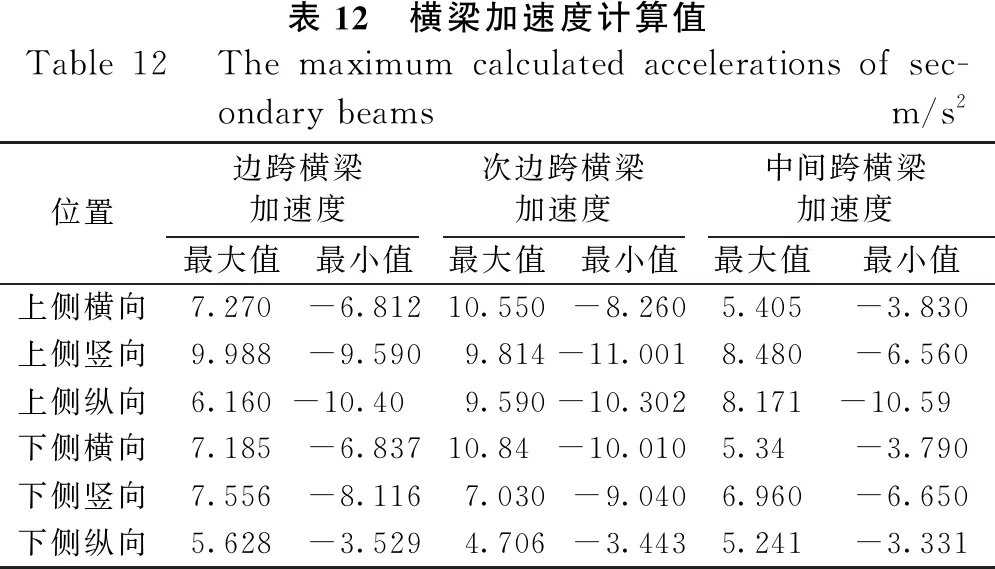
表12 横梁加速度计算值Table 12 The maximum calculated accelerations of sec-ondary beamsm/s2位置边跨横梁加速度次边跨横梁加速度中间跨横梁加速度最大值最小值最大值最小值最大值最小值上侧横向7.270-6.81210.550-8.2605.405-3.830上侧竖向9.988-9.5909.814-11.0018.480-6.560上侧纵向6.160-10.409.590-10.3028.171-10.59下侧横向7.185-6.83710.84-10.0105.34-3.790下侧竖向7.556-8.1167.030-9.0406.960-6.650下侧纵向5.628-3.5294.706-3.4435.241-3.331
4 结论
本文计算分析得到以下主要结论:
a.结构体系前6阶振型分析表明,第2阶振型中,边桩桥墩纵向弯曲,为桥墩沿纵向振动的主振型;第3阶振型中,边坡上侧的纵梁呈反对称竖向弯曲;第4阶振型中,上部梁体呈正对称变形,为纵梁竖向振动的主振型;第5阶振型中,只有边桩桥墩负向纵向弯曲;第6阶振型表现为桩体沿纵向,上部梁体沿竖向的复合振型。
b.桩体横向地震位移最大值11.9 cm,出现在边坡上侧的边桩桩顶位置,横向位移较小值4.15 cm,出现在边坡下侧的中间桩桩顶位置;对于同一纵向位置,边坡上侧的桩体位移较大,下侧边桩桩顶位移为上侧的49.2%;上侧边桩与下侧中间桩位移最大相差7.75 cm。
c.纵梁以横向位移反应为主,最大位移10.7 cm出现在边跨纵梁跨中位置,竖向和纵向位移为其10%~20%;坡体中位置不同的3根同跨纵梁横向位移差别不大。与相应位置纵梁相比,边跨横梁和次边跨横梁横向位移高1 cm左右,中间跨不明显。
d.桩体最大加速度为边坡上侧边桩桩顶横向加速度9.949 m/s2,比下侧边桩和中间桩桩顶高2.34和6.91 m/s2;竖向和纵向加速度最大值出现在边坡中部边桩桩顶位置,分别为9.81和8.54 m/s2;总体上,中间桩加速度反应相对较小,边坡上侧中间桩桩顶横向加速度仅为边桩的28.1%。
e.边坡上侧边跨纵梁竖向加速度11.1 m/s2为纵梁最大加速度值,边坡中部边跨纵梁纵向加速度6.1 m/s2,以及边坡下侧中间跨纵梁横向加速度6.0 m/s2,为纵梁较小加速度值;边坡上侧和下侧的边跨和次边跨纵梁加速度相差较小;中间跨纵梁各位置的横向加速度与边跨纵梁相差3.31 m/s2以上。
f.边坡上、下侧次边跨横梁横向加速度10.55和10.84 m/s2为横梁加速度中较大者,边坡上侧3根横梁的竖向加速度相差不超过1.5 m/s2,下侧相差不超过0.596 m/s2。边坡上侧3根横梁的纵向加速度中,次边跨横梁与边跨和中间跨横梁分别相差3.43和1.42 m/s2,下侧相差不超过0.92 m/s2。
