缝合复合材料VARTM注胶过程数值模拟

孙 煜，王晓旭，石 妍

（天津工业大学材料科学与工程学院，天津 300387）

0 引 言

缝合复合材料工艺始于二十世纪中后期［1］，是利用缝线穿过铺层织物的厚度方向，将铺层织物连接为准三维立体织物的工艺技术［2~3］，然后再经过一定的工艺成型技术制作成一种高性能的先进复合材料［4~6］。研究人员结合液体成型工艺［7］，对树脂传递模塑（RTM）［8］、真空辅助RTM（VARTM）［9］、树脂膜浸渗（RFI）［10］等制造工艺进行了深入研究。液体成型工艺中树脂存在空隙率较高，容易出现干纤维的现象，形成干斑、气泡等缺陷［11］。若通过模型模拟预测树脂流动前沿，充模时间等参数，则可有效避免此类缺陷［12］。

国内外已有众多学者开展了此类研究。王善凯等利用Moldflow 软件对注塑工艺进行了优化，所得较优的工艺改善了材料的翘曲变形［13］。李海晨等采用边界拟合坐标系和有限差分法模拟了两注射口的树脂流动过程，得到了树脂逐次流动的前沿和最后阶段的压力分布，为确定排气口提供了依据［14］。郭志昂等通过对VARTM注胶过程的数值模拟，得到了最佳的注射方案［15］。CORREIA 等利用流动模拟软件LIMS，模拟了出胶口压力对预制件压实和充填时间的影响［16］。HUANG 等利用三维数值模拟方法研究了树脂在复杂模具中的流动行为，在生产中减少了材料的内部孔隙［17］。SOUZA 等提出了利用有限体积方法最小化树脂流动的压力场与流动前沿位置不一致的方法。结果表明，提出的方法非常有效地确定了树脂流动前沿［18］。PHELAN建立了基于Darcy 定律的树脂传递模塑成型模拟方法，使用有限元方法求解每个连续流动前沿位置的控制方程集，仿真中加入了各种各样的元件类型，使得各种工业条件下的流动建模成为可能［19］。

本文建立缝合单胞模型和预制件板块模型，模拟树脂充填过程中位移与时间的关系，采用单向法计算出缝合预制件的渗透模拟值，通过实验验证其可靠性，并对其他缝合预制件的渗透率和充模时间做出预测。

1 实 验

1.1 材料与试剂

实验所用织物为面密度300 g/m2的玄武岩纤维平纹织物（常州桦立柯新材料有限公司）；缝线为线密度322 tex 的玄武岩纤维线（江苏天龙玄武岩连续纤维股份有限公司）；树脂和固化剂分别为RIMI 1040 型号环氧树脂、RIMI 1048 固化剂（瀚森化工企业管理有限公司）。

1.2 玄武岩纤维预制件的缝制

本研究中的纤维预制件为缝合的玄武岩纤维织物，制件大小为300 mm×250 mm×7.2 mm，铺层数为24 层，缝合方式为单缝线式缝合，缝合间距为4 mm。

1.3 测试及计算方法

渗透率的测试方法如图2所示，树脂在真空压差下开始流动充填待测件，x为树脂流动方向，P0为大气压。拍摄记录树脂流动前沿，根据所记录的摄像，观察不同时刻下树脂的流动前沿位移，通过计算流动前沿的位置计算渗透率。

图2 渗透率测试实验原理示意图Fig.2 Schematic diagram of the experimental principle of permeability testing

树脂对预制件浸润的前提条件是树脂的流动，树脂在预制件的流动过程可被描述和处理为牛顿流体在多孔介质中的流动，从而符合Darcy定律。Darcy 定律将流体流速、渗透率张量、流体压力梯度、液体黏度相互关联，如式（1）所示：

式中：q为单位面积流体流动速度，m/s；k为渗透率，m2；▽p为流体压力梯度，Pa；μ为流体黏度，Pa·s。

本实验中渗透率测试采用恒压测试法，在压力、树脂黏度恒定不变的条件下，记录树脂从注胶口流出后不同时刻下的流动位移，计算公式如下：

式中：K为纤维预制件的渗透率张量，m2；t为时间，s；ΔPi-o为注胶口与出胶口之间的压力，Pa；L为流体流动前沿的距离，mm。

2 玄武岩预制件渗透率

对缝合间距为4 mm 的预制件和未缝合的预制件分别进行VARTM工艺树脂充填，并通过摄像机记录树脂的流动情况，实验采用定距记录数据的方式记录树脂每30 mm 的流动位移下所花费的时间，计算预制件的渗透率。玄武岩纤维预制体的渗透过程如图3所示。

图3 玄武岩纤维预制体的渗透过程Fig.3 The infiltration process of the basalt fiber preform

2.1 未缝合玄武岩预制件渗透率的测定

未缝合的玄武岩纤维铺层的树脂流动前沿位移数据记录如表1所示。

表1 未缝合玄武岩纤维铺层树脂充填流动前沿位移Tab.1 Displacement of the resin filling flow front at time of the unstitched basalt fiber layer

树脂流动位移L2x与时间存在线性关系，线性拟合可得如图4 所示的L2x-t拟合图。由图4 可知直线斜率为0.091 2，根据式（2）可计算得未缝合预制件的渗透率为4.48×10-11m2。

图4 未缝合玄武岩纤维预制体的-t 拟合曲线Fig.4 The -t fittingcurveof unstitchedbasaltfibrepreform

2.2 缝合玄武岩预制件渗透率的测定

缝合的玄武岩纤维铺层的树脂流动前沿位移数据记录如表2所示。

表2 缝合玄武岩纤维铺层树脂充填流动前沿位移Tab.1 Displacement of the resin filling flow front at time of the stitched basalt fiber layer

同理，对树脂流动位移L2x与时间t作图，可得图5所示的L2x-t拟合图。

图5 缝合玄武岩纤维预制体的-t 拟合曲线Fig.5 The -t fitting curve of stitched basalt fibre preform

同理，根据式（2）计算得出缝合后的待测件渗透率为6.14×10-11m2。未缝合的预制件与缝合间距4 mm 的预制件制得的样品质量良好，表面无气泡、干斑等缺陷。两者的线性变化趋势整体相同，与未缝合的预制体相比，缝合间距为4 mm的预制件渗透率提高了37%，缝合玄武岩纤维织物的渗透时间小于未缝合玄武岩纤维织物，下面通过数值模拟进一步分析缝合预制件的渗透规律。

3 数值模拟

3.1 模型建立

3.1.1 单胞模型

为了更好地观察和分析模型内部树脂的充填渗透情况，利用PAM-RTM对缝合单胞模型充填渗透过程进行模拟，建立了以缝合玄武岩纤维预制件的单胞模型，织物厚度为0.3 mm，缝合间距为4 mm，铺层角度为0°/45°/90°/-45°。图6为单胞模型，菱形深色区域为缝线将面内纤维挤开所产生的孔隙，圆柱区域为缝线等效模型。将壳体模型导入后处理软件hypermesh 中进行网格划分，网格类型为三角形网格，有限元网格单元数为15 738。

图6 缝合单胞模型Fig.6 Stitched unit-cell model

3.1.2 板块模型

将缝合间距为4 mm的12个单胞组合，构成缝合预制件的板块模型，如图7 所示，尺寸为16 mm×12 mm×1.2 mm。本模型有限元网格单元数为76 673，网格节点数为16 216。

图7 缝合板块模型Fig.7 Stitched plate model

将画好网格的单胞模型导入PAM-RTM软件中，选用的增强材料参数为实验值，孔隙渗透率参考文献［20］，具体参数见表3。

表3 材料属性及工艺参数Tab.3 Material properties and process parameters

3.2 单胞模拟结果分析

图8为缝合单胞模型树脂充填分析剖视图，蓝色表示未充填区域，红色表示已充填区域，黄绿色代表树脂流动前沿。图8（a）为充填前模型的剖面内部结构，图8（b）~（f）为不同时刻树脂单胞模型中流动充填的情况剖面图。从图中可以得到：纤维预制件表面树脂前沿超前于内部；树脂流经孔隙区域时，充填速度较快；孔隙区域最先完成浸润，其次是缝线区域，最后是纤维织物区域。主要原因是树脂在充填的过程中，空隙中由于没有纤维阻力的存在，所以树脂流动速度较快，尤其是厚度方向上的充填流动。

图8 缝合单胞模型树脂充填分析剖视图Fig.8 Cross-sectional view of resin filling analysis of sutured unit-cell model

3.3 缝合模型工艺验证

图9 为缝合间距为4 mm 的树脂充填云图，缝合纤维预制件板块模型的流动形状受到缝线及孔隙形状的影响，流动前沿呈不规则形状，充填时间为1.9 s。

图9 充填时间云图Fig.9 Cloud chart of filling time

根据充填时间云图可得树脂流动位移与时间表，通过PAM-RTM模拟其树脂充填过程得到充填位移时间的函数关系，计算得到板块模型的渗透率，从而得到整体缝合纤维预制件的渗透率，图10 为树脂流动位移的平方与时间的关系图。

图1 缝合玄武岩纤维预制件Fig.1 Stitched basalt fiber prefabrications

图10 树脂流动位移的平方与时间的关系图Fig.10 The relationship between the square of resin flow displacement and time

根据式（2）计算可知，缝合间距为4 mm 的纤维预制件的渗透率为6.27×10-11m2，实验结果为6.14×10-11m2，相对误差为2.07%，说明通过数值模拟法来计算缝合纤维预制件的渗透率具有一定的可行性。可能造成误差的原因有：1）在计算机模拟中没有考虑毛细渗透压力，毛细渗透压力与渗透率呈负相关，造成模拟值偏大；2）未考虑树脂的黏度的变化。

3.4 不同缝合间距模拟结果分析

缝线孔隙可以提高树脂的流动速度，减少树脂的充模时间，缝合间距对VARTM工艺中树脂充填过程的影响也是后续研究的重点之一，为了得到不同缝合间距下的渗透率，通过PAM-RTM软件对缝合间距为3、4、5、6 mm 的纤维预制件的板块模型进行渗透率的模拟计算，图11 为不同缝合间距树脂充填时间云图。

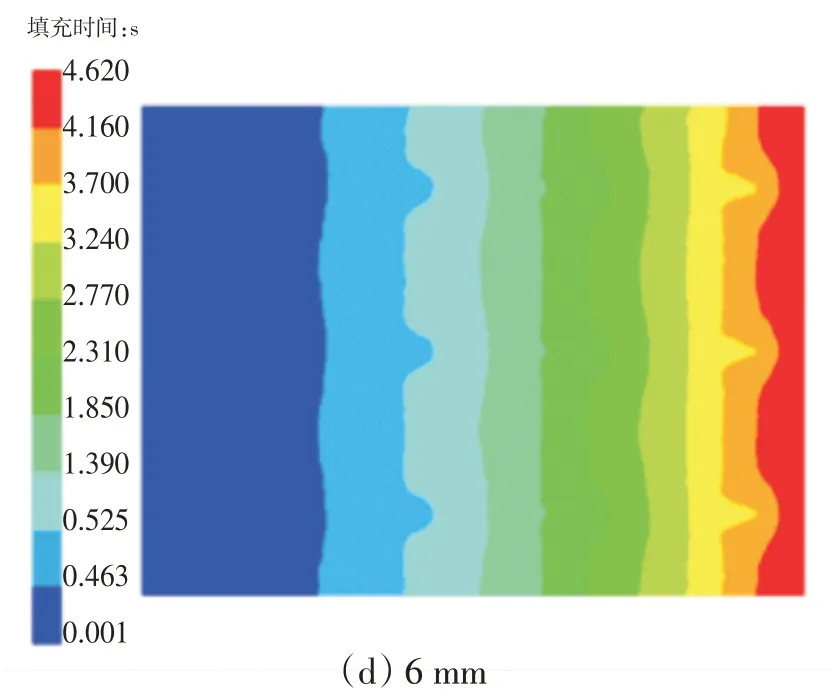
图11 充填时间云图Fig.11 Cloud chart of filling time

在充填过程中，由于边缘效应树脂先沿着预制体表面浸润纤维预制件，同时树脂还沿着厚度方向进行浸润，缝线和缝孔的存在加速了树脂浸润的过程。由图11可知，缝合间距为3、4、5、6 mm的缝合纤维预制件板块模型的充填时间分别为0.945、1.90、3.16、4.62 s，可以看出缝合间距越小，充填时间越短，尤其是缝合间距为3 mm的预制体，充填时间缩短了90%。

从图11中还可看出，树脂的流动前锋为锯齿状，并且缝合间距越小，峰值越尖锐。这是由于树脂在缝孔中没有纤维阻力，流动速度较快，而树脂在纤维面板间的纤维流动阻力较大，这种流动速度的不一致性，导致流动前锋为锯齿状。如图11（a）所示，缝合间距为3 mm×3 mm预制体中，树脂在纤维面板的流动速度明显滞后于缝孔，缝合间距的降低可以加快树脂流动速度，同时面板与缝孔间也会增加树脂流动速度的不一致性程度，这可能会导致包围现象［21］，成型的制品中较易产生干斑或气孔，影响复合材料质量。

图12 为树脂流动位移与时间的关系，根据模拟充填所得到的位移充填时间云图，分别取10个点，绘制-t曲线。计算得到各个缝合间距下的渗透率，结果如表4所示。

表4 不同缝合间距的缝合纤维预制件板块模型的渗透率Tab.4 Permeability of stitched fiber preform plate model of different stitch spacings

图12 不同缝合间距的缝合纤维预制件板块模型的-t图Fig.12 The -t curve of the stitched fiber preform plate model of different stitch spacings

从图12 和表4 可以看出缝合间距越大，渗透率值越小。是因为缝合间距越大，缝线孔隙越少，树脂的流动通道减少，渗透率就相对降低，也由此说明缝合间距的减小有利于树脂的流动。

4 结 论

通过对VARTM 工艺下不同缝合间距纤维预制体树脂流动的模拟仿真分析，得出以下结论：

1）缝合间距为4 mm 的预制件渗透率比未缝合预制件的渗透率提高了37%。

2）树脂流经孔隙区域时，由于没有纤维阻力的存在，充填速度较快，尤其是厚度方向上的充填流动；孔隙区域最先完成浸润，其次是缝线区域，最后是纤维织物区域。

3）渗透效果受缝合间距影响，缝合间距越小，缝线孔隙越多，树脂的流动通道增加，渗透率就越高。但缝合间距越小，容易增加树脂流动的不一致性程度。