CCl+分子离子激发态的显关联组态相互作用研究

国慧杰，姜 文，李 瑞，艾瑞波，赵书涛

(1.齐齐哈尔大学 理学院，黑龙江 齐齐哈尔 161006；2.阜阳师范大学 物理与电子工程学院，安徽 阜阳 236037)

引言

卤代碳等离子体在蚀刻领域中非常重要，因为其有望在半导体和其他需要细线光刻的设备制造中得到广泛的应用[1,2]。作为卤代碳等离子体反应中出现的离子，如反应性He/CCl4/CHCl4等离子体环境，CCl+在测定等离子体的温度和化学性质方面被证明是有价值的探测体系。获得CCl+准确的电子结构数据有助于更好地理解和发展等离子体蚀刻技术。电子态的电子结构和光谱性质在先前对一卤化碳离子（CF+，CBr+和CI+）的实验和理论研究中受到了相当大的关注。

在实验方面，Huber 和Herzberg 总结了基态X1Σ+和11Π 态的光谱常数[3]。1961 年Verma 等人[4]通过在四氯化碳蒸气中使用高频放电方法对11Π-X1Σ+跃迁的转动结构进行研究，并讨论相关电子态的组态成分。在1983 年，Bredohl 等人[5]采用微波放电法重新研究了11Π-X1Σ+的跃迁发射光谱，并确定其转动常数。同年，Tsuji 等人[6]通过He+与CCl4的电荷转移反应中，在230-255 和390-405 nm 区域观察到了CCl+的跃迁谱带分别是11Π-X1Σ+和13Π-X1Σ+，并确定了X1Σ+，11Π 和13Π态的光谱常数。Gruebele 等人[7]报道了CCl+自由基的Born-Oppenheimer 势能函数和基态的光谱常数，并采用振转薛定谔方程直接数值积分方法对卤代烃CCI+和CF+的势函数进行了更详细的分析[8]。Reid[9]将平动能光谱应用于CCl+离子的碰撞激发和电荷反转反应中，以确定CCl+激发态相应能量和键长信息。2021 年Asvany 等人[10]利用低温离子阱装置首次观测到CCl+(X1Σ+)阳离子的纯旋转光谱。

在理论方面，Nishimura 等人[11]采用从头算LCAO-SCF-MO 组态相互作用方法，计算了CCl+，SiCl+和GeCI+离子的X1Σ+，11Π 和13Π 态的势能曲线以及光谱常数Te，ωe和ωeχe。Peterson 等人[12]采用Moller-Plesset 多体微扰理论计算了双原子体系BC1，CS，CCl+，BF，CO，CF+，N2，CN 和NO+的光谱性质。Šurkus[13]利用Gruebele 等人得到的光谱信息建立了CCl+基态的势能函数。1990 年Peterson 等人[14,15]利用组态相互作用方法研究了势能和偶极矩函数。2013 年Zhang[16]通过采用MRCI+Q/AV5Z 从头计算方法研究了CCl+的低激发电子态，报道了12 个Λ-S 电子态和23 个Ω 态的势能曲线和光谱常数的性质。

综上所述，对CCl+分子离子的低激发电子态进行了一系列研究。关于低激发态的电子结构和光谱信息仍然较为有限，精确度需要进一步提高。在这里，我们基于高水平MRCI-F12 对CCl+离子的电子态进行理论研究。用MRCI-F12 方法计算与CCl+离子最低解离极限相关的12 个Λ-S态的PECs。基于计算的PECs，获得束缚态光谱常数。计算PDMs，TDMs，FCFs 和辐射寿命。

1 计算方法

在本次工作中，使用MOLPRO 2012[17]量子化学从头算程序包对CCl+分子离子的电子结构进行了从头计算。对于核间距R=1.35-4 Å 计算步长选择为0.05 Å，对于R=4-5 Å 计算步长选择为0.1 Å，对于5-7 Å 计算步长选择为1 Å。计算中C+和Cl 均采用cc-pVQZ-F12[18]基组。为了获得精确的低激发电子态PECs，电子结构的计算通过以下三个步骤进行:首先，利用Hartree-Fock 自洽场方法计算CCl+基态的分子轨道，并将其作为后续高精度计算方法的初始波函数。然后利用完全活性空间自洽场(CASSCF)[19,20]方法对得到的Hartree-Fock 分子轨道进行优化，得到了CCl+基态和激发态的多组态波函数。在后续的组态相互作用计算中，CASSCF 轨道作为参考轨道。最后，在CASSCF 波函数的基础上，采用MRCI-F12[21]方法，进一步考虑电子动力学的相关影响，得到高精度的能量和波函数。在计算过程中，采用戴维森修正(Davidson(+Q))[22]去校正MRCI 方法的大小不一致性。

在本次计算中，采用了C∞v点群的阿贝尔子群C2v群的不可约表示来描述CCl+的电子态。对应的两个点群之间不可约表示关系分别是：Σ+=A1，Π=B1+B2，Δ=A1+A2，Σ-=A2。CCl+选择4a1、2b1、2b分子轨道作为活性空间来构建电子态波函数。活性空间中的分子轨道对应于C+的2s、2p 轨道以及Cl 的3s3p 轨道。应用MRCI-F12 方法计算得到了最低解离极限对应的4 个Σ+态，2 个Σ-态，2个Δ 态和4 个Π 态，共12 个Λ-S 态。

根据Λ-S 态的PECs，借助LEVEL 程序[23]求解一维核Schrödinger 方程，确定这些态的相应光谱常数，包括绝热激发能Te，平衡核间距Re，平衡振动频率ωe和一阶非谐性常数ωeχe，平衡转动常数Be。解离能De是通过从解离极限处的能量中减去平衡核间距Re处的分子能量而获得的。我们通过计算电子态之间的FCFs 获得了PDMs 和TDMs。基于FCFs 和TDMs，计算得出辐射寿命,分子体系的光谱性质研究一直以来备受关注[24-26]。

2 结果与讨论

2.1.Λ-S 态的光谱常数和势能曲线

使用MRCI-F12 方法计算出CCl+最低解离极限(C+(2Pu)+Cl(2Pu))相关的12 个Λ-S 态。CCl+体系Λ-S 态的PECs 绘制在图1(a，b)中。为了清楚地显示电子态的相对位置，在图1 的(a)和(b)中分别给出了单重态和三重态的PECs，另外，为了比较，在这些图中均给出了基态的PEC。从图1 中可以看到，11Π 和13Π 态的PECs 形状和平衡核间距都非常相似。这是因为在Re处11Π 和13Π 的主要电子组态相同，均为 6σ27σ18σ01π42π43π1和6σ27σ18σ01π42π33π2。表1 列出了束缚态的光谱常数及其在Re处的主要电子组态。

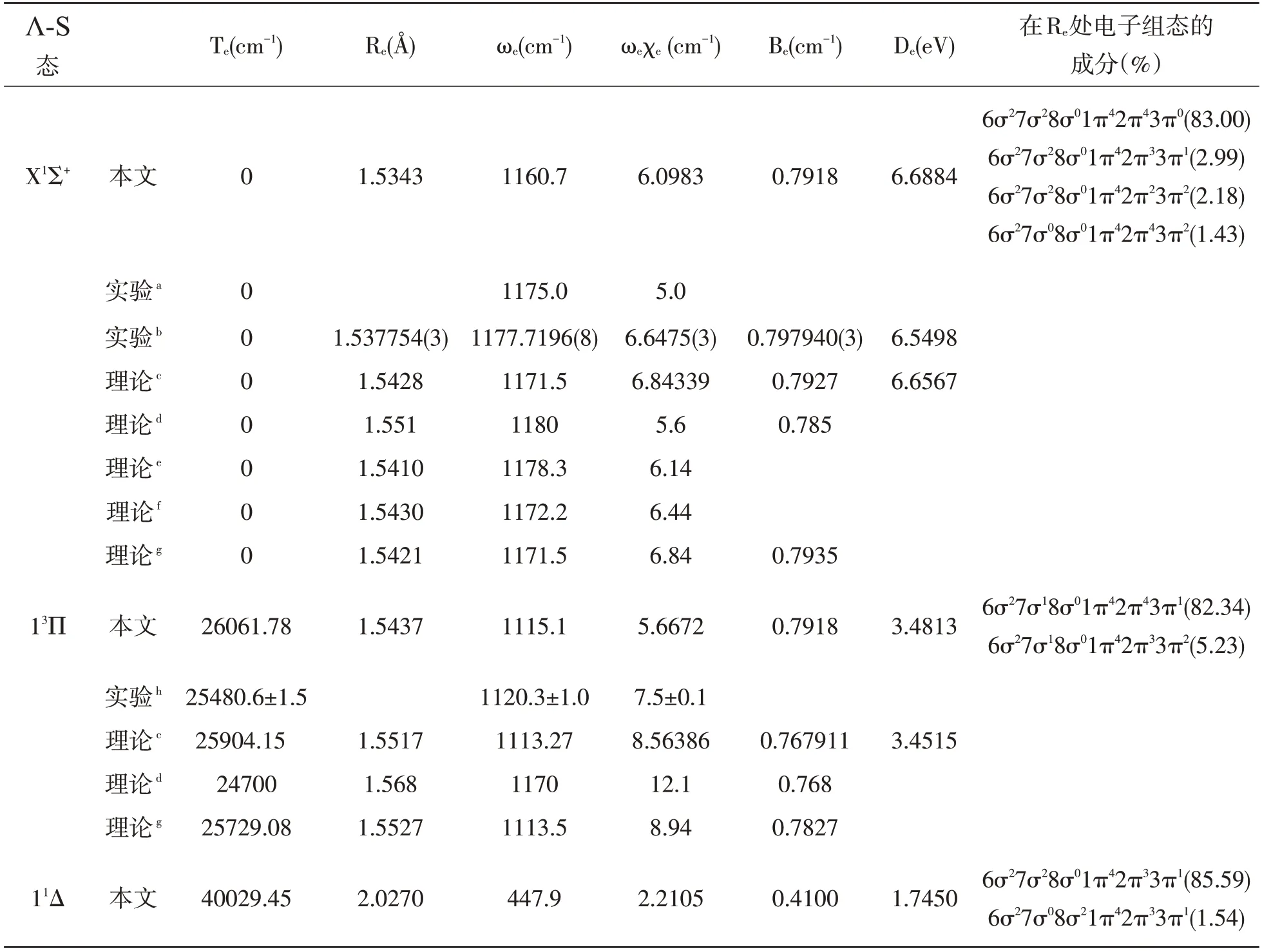
表1 CCl+分子离子Λ-S 态的光谱常数

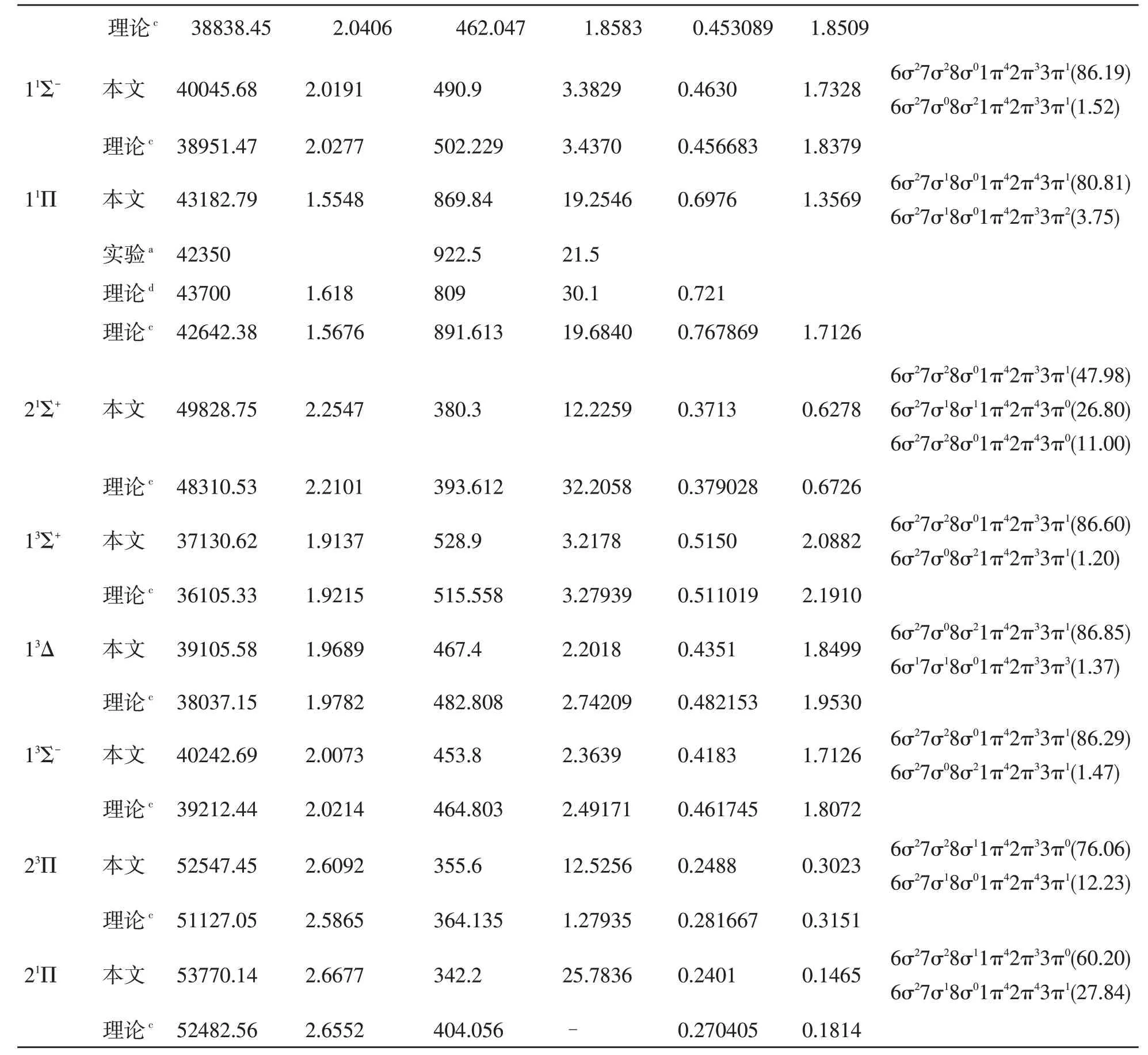
a文献[3],b文献[7],c文献[16],d文献[11],e文献[12],f文献[14],g文献[15],h文献[6]

CCl+的基态是X1Σ+态，在平衡核间距位置主要电子组态为6σ27σ28σ01π42π43π0。我们将Re的结果与现有的实验结果[7]进行比较，偏差为0.0035 Å（0.23%）。在先前的工作中发现了关于基态X1Σ+的De实验值[7](6.5498 eV)，理论值[16](6.6567 eV)，我们的计算值(6.6884 eV)比上述两个值都要大但更接近于理论值。本文的理论计算给出的X1Σ+的De为6.6884 eV，与实验值和理论值之间的偏差分别为0.1386 和0.0317 eV,误差仅为2.1%和0.48%，MRCI-F12 计算的得到的结果与实验值和理论值符合的都很好。该电子态的势阱较深，能够存储75 个振动能级。

如图所示，尽管CCl+自由基具有12 个Λ-S态，但只有13Σ+态属于完全排斥态。图1(a)描述了单重态的PECs，从图中我们可以观察到11Δ和21Σ-的势能曲线几乎重合。11Π 与多条势能曲线相交，这些交叉的态之间可能会发生很强的相互作用。11Π 与21Π 态在R=2.6 Å 附近出现避免交叉。图1(b)描述了三重态的PECs，从图中我们可以看出13Π 与多条势能曲线发生交叉，并与23Π在R=2.7 Å 附近发生避免交叉。

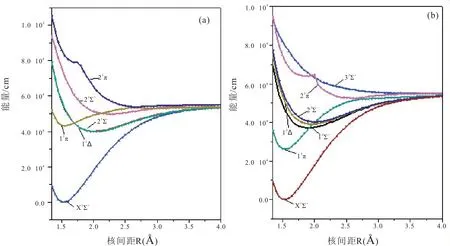
图1 CCl+分子离子Λ-S 态势能曲线，(a)单重态，(b)三重态

11Π 和13Π 态的解离能为1.3569 和3.4813 eV。对于11Π 和13Π 态，电子组态表现出相似的多组态特征。对于13Π 态，我们计算的Te和ωe值为26061.78 和1115.1 cm-1，与先前的实验值[6]25480.6±1.5 和1120.3±1.0 cm-1符合得很好，误差分别在2.3%和0.5%之内。对于11Π 态，我们计算Re的结果与其他理论值[11,16]之间的误差均小于4%。

如图2 所示，基于MRCI-F12 波函数，计算了12 个Λ-S 态在核间距1.35 到4.0 Å 范围的PDMs。计算的正方向是从C+到Cl。从图中可以看出这些态的PDMs 随着核间距的增加逐渐增大。此现象表明解离极限对应的解离产物是C+离子和Cl 原子。

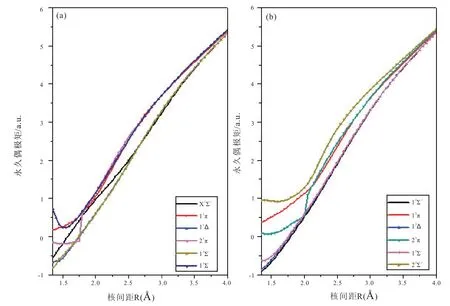
图2 Λ-S 态的永久偶极矩曲线

2.2 Λ-S 态自旋轨道矩阵元

如图3 和图4 所示，我们给出了基态和几个低激发态的PECs 和SO 矩阵元。从图3 我们可以看出13Π 和11Π 的PECs 与11Δ，13Δ，13Σ+，11Σ-和21Σ+态的PECs 相交。图4 显示了与13Π 和11Π 态相关的SO 矩阵元随R 的变化曲线。SO 矩阵元在R=3.5 Å 附近趋于水平。除13Π-21Σ+和11Π-23Π外，其余均在R=2.5 Å 附近达到最大值，然后随着R 的增大逐渐减小。13Π 和11Π 的PECs 与11Δ，13Δ，13Σ+和11Σ-处于交叉点时SO 矩阵元均在100 cm-1附近，说明13Π 和11Π 态与11Δ，13Δ，13Σ+和11Σ-态的相互作用较强。从图中可以看出13Π 态和21Σ+态的势能曲线不相交，而13Π-21Σ+的SO 矩阵元最大。在高密度电子态区域，电子态之间可能存在更复杂的自旋轨道耦合相互作用。

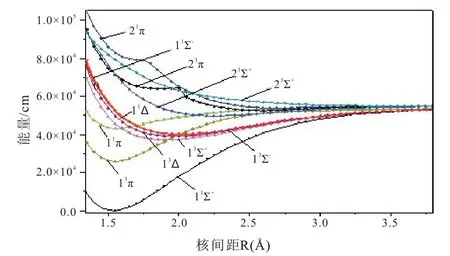
图3 CCl+离子Λ-S 态势能曲线交叉区域

图4 CCl+离子与13Π 和11Π 态相关的自旋轨道矩阵元

2.3 Λ-S 态的跃迁性质

将21Π 和11Π 在核间距R=1.3-3.5 Å 范围内相关的跃迁偶极矩展示在图5 中。从图中可以看出21Σ+-X1Σ+的跃迁偶极矩最大，并随着核间距的增加先增加并在R=1.65 Å 时达到最大值0.64 a.u.，然后随着核间距的增加TDM 逐渐减小。11ΠX1Σ+和13Π-X1Σ+跃迁偶极矩变化趋势相似，均随核间距的增加而逐渐减小。

图5 CCl+离子激发态的跃迁偶极矩

在表2 中计算并列出了11Π-X1Σ+和13Π-X1Σ+的FCFs 值。由于13Π-X1Σ+跃迁带的对角线因子接近于1，上、下电子态的Re值非常接近，所以11Π-X1Σ+的FCFs 小于13Π-X1Σ+的FCFs 的值。13Π-X1Σ+的FCFs 高度对角化满足了双原子分子激光冷却的标准之一。而上态13Π 的自发辐射寿命在毫秒级（表3），对于冷原子来说光学周期太长，存在很大困难。对于11Π 的Re约为1.5548 Å，比基态的Re短0.02 Å，因此这些态与基态之间的FCFs 比13Π-X1Σ+对角线的值小，如表2 所示。

表2 CCl+离子激发态11Π-X1Σ+和13Π-X1Σ+跃迁的Franck-Condon 因子

基于理论得到的电子态之间的能级差、TDMs和FCFs，根据以下公式计算跃迁的辐射寿命，公式如下：

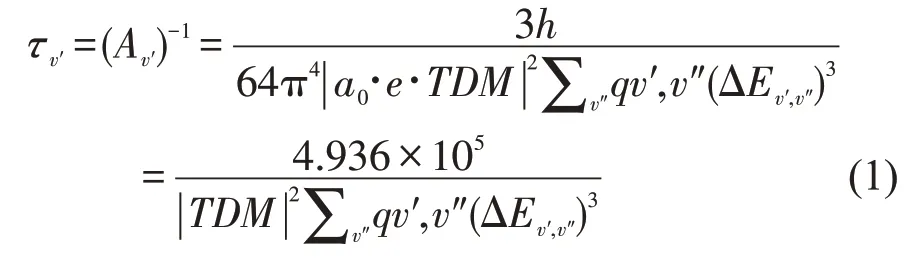
式中qv′,v″为Frank-Condon 因子，TDM 以原子为单位(a.u.)，能量差以cm-1为单位，τ 表示辐射寿命以ns 为单位，ΔE分别表示′和′之间的能级差。11Π-X1Σ+和13Π-X1Σ+跃迁的辐射寿命在表3中列出。计算得出的11Π-X1Σ+和13Π-X1Σ+的辐射寿命处于ns 的数量级。

表3 CCl+离子激发态的辐射寿命

3 结论

本文采用高精度的MRCI-F12 方法研究了CCl+分子离子12 个Λ-S 电子态的PECs，分析了CCl+分子离子体系的电子结构和光谱性质。根据计算得到的PECs，求解径向Schrödinger 核运动方程，得到了束缚态的光谱常数，并与实验值吻合较好。通过我们的结果可以看到CCl+分子离子的一些束缚态的PDMs 是正值，并在核间距大的范围处产生渐近线性，这与C++Cl 的解离极限相对应。我们还计算了SO 矩阵元来分析了13Π 和11Π 与11Δ，13Δ，13Σ+，11Σ-和21Σ+态的相互作用。此外，还获得了包括TDMs、FCFs 和辐射寿命的跃迁性质。为后续进行CCl+分子离子精确光谱性质的研究提供参考。