基于扩展状态观测器的三相PWM整流器控制研究
2022-04-02刘俊伟
刘俊伟
(陕西理工大学,陕西 汉中 723000)
0 引言
三相PWM整流器具有功率因数高、功率开关管电压、电流应力小以及功率流可双向流动等优点,因而被广泛地应用于中大功率的工业场合中[1]。目前,大多数三相PWM整流器采用基于dq坐标系的双环PI控制方法,但PI控制普遍存在对变化负载不具有良好的控制性能[2]。文献[3]采用比例谐振控制进行控制器设计,实现了静止坐标系下的三相整流器控制,但是所需设计的控制参数过多,参数调试过程十分复杂,且对变化负载不具有良好的鲁棒性。文献[3-7]分别采用反馈线性化、李雅普诺夫稳定性原理和无差拍控制设计了相应的控制器,实现了三相整流器的高性能控制,但在负载发生变化时整流器控制性能依然不佳。
三相整流器运行过程中所带负载将会随着运行状态实时地发生变化。为了保证整流器具有良好的输出电压调节性能,所设计的控制器必须对负载变化具有良好的自适应能力。为此,本文建立了三相整流器的dq数学模型,设计了三相整流器的双环PI控制器。针对负载频繁发生变化的问题,基于扩展状态观测器理论设计了电压环控制器。该控制方案无须改变三相整流器的双环PI控制结构,实现了对负载变化具有更好的适应能力,仿真结果验证了所提控制方法的有效性和可行性。
1 三相PWM整流器数学模型
三相PWM整流器拓扑结构如图1所示。其中,Ua,Ub和Uc为三相输入电源电压,ia,ib和ic为三相输入电流,La=Lb=Lc=L为交流滤波电感,电阻r为交流电感和功率开关管的等效电阻,C为输出滤波电容,R为直流侧负载。

图1 三相PWM整流器拓扑结构
定义三相整流器的开关函数为Si(i=a,b,c)。其中,Si=1表示第i桥臂的上桥臂功率开关管开通,下桥臂的功率开关管关断;Si=0表示第i桥臂的上桥臂功率开关管关断,下桥臂的功率开关管开通。
依据图1,结合KVL和KCL定律,可得ABC静止坐标系下的三相PWM整流器数学模型为:

通过对式(1)进行dq坐标变换,可得三相PWM整流器的dq数学模型为:
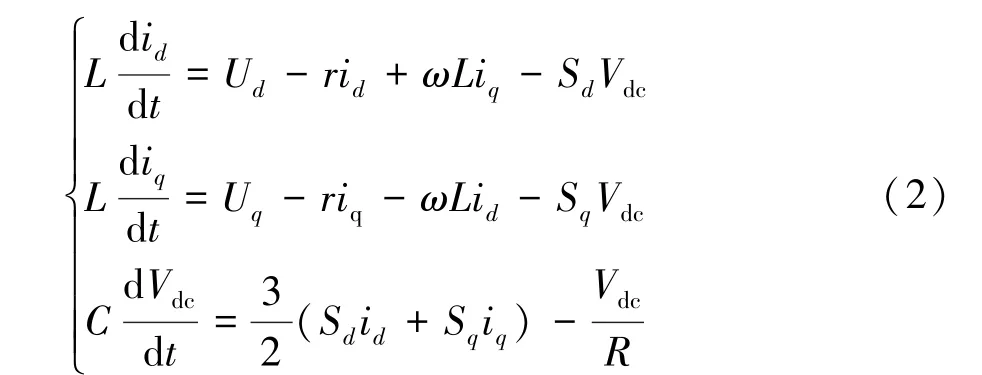
式中:ω为三相输入电源电压的角速度;Ud和Uq分别为电压有功和无功率分量;id和iq分别为电流有功和无功率分量;Sd和Sq为开关函数在d轴和q轴上的开关分量。
2 三相PWM整流器双闭环控制器设计
目前,三相PWM整流器的控制器主要采用电压、电流双闭环控制结构。其中,电压外环主要用于控制和稳定整流器输出电压,电流内环主要用于跟踪给定电流,同时实现单功率因数控制。
2.1 电流内环控制器设计
依据式(2)可得整流器的电流环方程为:
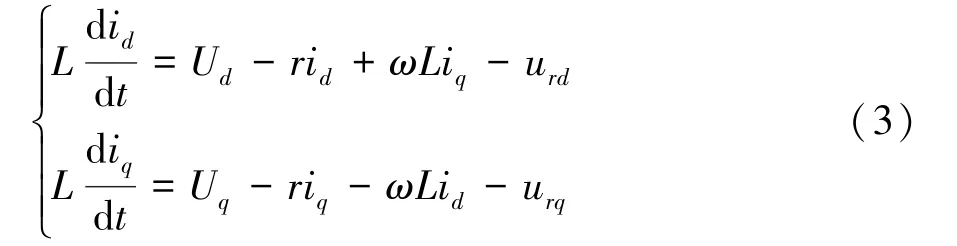
式中:urd=SdVdc,urq=SqVdc,为三相整流系统控制输入量。结合前馈解耦PI控制思想,进一步可设计如下的电流控制器:

式中:idref和iqref为d轴和q轴电流参考量;ed=ididref,eq=iq-iqref;kpd、kid、kpq和kiq为电流环控制参数且均大于0。将式(4)代入式(3)可得电流闭环系统方程为:
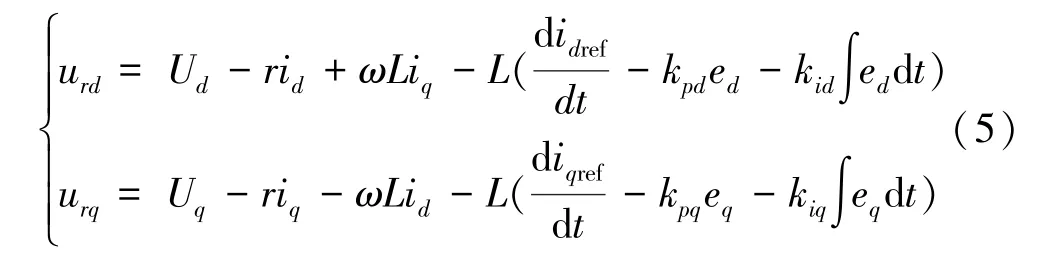
由式(5)可以看出,通过对参数kpd、kid、kpq和kiq合理的设计,该系统是能够实现稳定的。
2.2 电压外环控制器设计
三相PWM整流器一般运行于单功率因数状态,即三相对称电压与三相输入电流同相位,此时iqref=0。考虑到电流环的响应速度远远大于电压环,因此在设计电压环时可认为电流环已经完全跟踪上了参考电流。因此,式(2)中的电压环方程可被改写为:

式中,Urdc=Sdid,fdc=Vdc/(RC)。对于采用PI控制的电压环,fdc一般不予考虑,通常被认为是系统外部扰动,即fdc项在式(6)中视为0。为此,依据PI控制思想,同时结合式(6)可得电压环控制器为:

式中:Vdcref为整流器输出电压给定值,edc=Vdcref-Vdc;kpdc和kidc为控制参数且均大于0。将式(7)代入式(6)得:

由式(8)可知,fdc为0时,通过对kpdc和kidc进行合理的设计,电压环能够实现渐进稳定。然而fdc中的负载R通常随着系统运行情况而发生变化,fdc将对整流器输出电压的稳态、动态性能产生影响。
假设系统能够对fdc进行实时估计,同时在电压环控制器中给予前馈补偿,则式(8)将被改写为:

式中,fdccomp为fdc的在线估计值。式(9)表明,通过对fdc在线估计和前馈补偿,能够有效地降低fdc对输出电压控制性能的影响。
2.3 电压环ESO设计
为了实现对fdc的在线估计,Luenberger观测器被广泛地采用。然而,Luenberger观测器实质为一种预测器-校正器结构,通常需要模型信息来构建Luenberger观测器。在建模误差较大的情况下,Luenberger观测器往往会变得不稳定,从而影响整个控制系统的稳定性和鲁棒性。相对于Luenberger观测器,ESO独立于被控对象的数学模型,构建更简单,效率更高,更易于实现,同时也不受参数变化和外部干扰等模型不确定性的影响[8]。因此,本文选用ESO对扰动fdc在线估计。
ESO设计的关键是将扰动fdc视为控制对象的附加状态,对于一阶系统,其状态变量数目从1个增加为2个。基于此,本文选择如下状态变量:

由式(6)和式(10)可得系统扩展状态方程为:

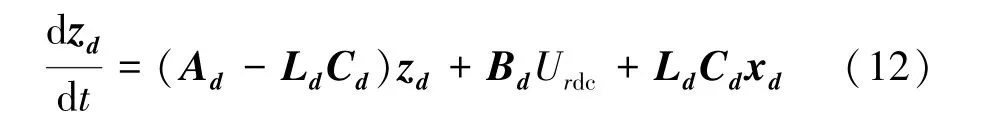
式中:Ld=[β1dβ2d]T为观测器的控制参数且Ld>0;zd=[z1dz2d]T为xd的估计值。
由式 (11)和式(12)可得ESO动态误差方程为:

由式(13)可得Ae的特征方程为:

式(14)表明,选取合理的参数β1d和β2d可使Ae的特征根位于相平面的左半平面,从而使所设计的ESO实现稳定。由式(12)也可以看出,Ad和Bd均为常数且不依赖于控制对象的具体信息,因而ESO的增益也将独立于控制对象,这有效地提高了ESO在三相整流器应用中的工程实用性。
3 仿真结果及分析
系统参数分别为:L=9 mH,r=0.1 Ω,C=4600 μF;输入交流电压的相电压峰值为55 V,输出目标电压为200 V,额定负载为29 Ω。为了验证本文所提控制方法的有效性和优越性,本文与传统的双环PI控制方法进行仿真对比,两种控制方法均选取相同的PI控制参数,同时β1d和β2d分别选取为1200和120050,仿真结果如图2和图3所示。

图2 传统双环PI控制下输出电压暂态响应

图3 带ESO双环PI控制作用下的输出电压暂态响应
由图2可知,在传统双环PI控制作用下整流器的输出电压过渡过程约为0.35 s,电压压降约为14 V。由图3可知,在带ESO的双环PI控制作用下整流器的输出电压过渡过程约为0.1 s,电压压降约为7 V。与此同时,两种控制方法的输出电压稳态误差均在0.6 V以内。以上结果表明,两种控制方法作用下的三相整流器均具有良好的输出电压稳态、动态性能。但相比而言,本文所提控制方法具有更快的电压调节速度和更小的电压压降。由此表明,通过增加ESO确实可有效地提升控制器的控制性能。这是由于本文所提控制方法通过ESO对整流器负载进行了实时观测并进行了前馈补偿,因而整流器的输出电压控制的稳态和动态性能得到了大幅度的提高。
图4和图5为稳态时两种控制方法作用下电网电流仿真波形。图4中电网电流的THD为0.8%,图5中电网电流THD为0.85%,在两种控制方法作用下电网电流THD相近。由此表明,本文所提控制方法不会显著地增加电网电流的THD,具有良好的工程实用性。
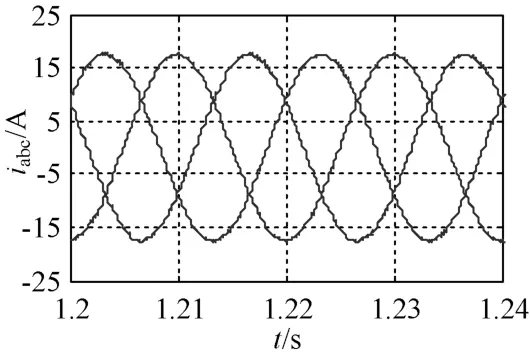
图4 传统双环PI控制作用下的电网电流稳态波形
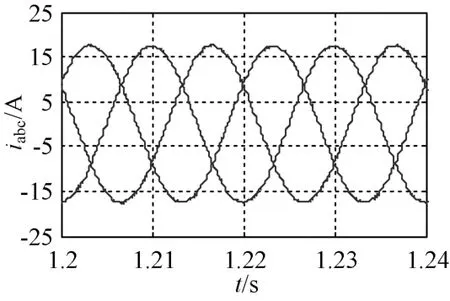
图5 带ESO双环PI控制作用下的电网电流稳态波形
4 结语
针对传统双环PI控制在三相整流器应用中不具有良好的负载自适应能力,本文提出了一种基于ESO的双环PI控制方法,实现了三相整流器控制。与传统双环PI控制方法相比,本文所提控制方法无须改变传统双环PI控制的控制结构,在负载变化时具有更强的自适应能力和更好控制效果,电网电流THD并未显著地增加。因此,所提控制方法具有更好的工程应用价值。
