基于CWI方法的门源MS6.9地震余震定位研究
2022-04-02张胜霞尹欣欣王祖东陈晓龙王树旺鞠慧超李阳阳王维欢
张胜霞, 尹欣欣, 王祖东, 陈晓龙, 蒲 举, 王树旺, 鞠慧超, 李阳阳, 王维欢
(1. 甘肃兰州地球物理国家野外科学观测研究站, 甘肃 兰州 730000; 2. 甘肃省地震局, 甘肃 兰州 730000)
0 引言
中国地震监测台网在西北地区监测站分布稀疏,尤其是地广人稀的祁连山脉一带,这对于要求台站分布密集的传统定位方法而言,很难给出准确地震位置,因此传统定位方法在台站分布稀疏地区具有一定的局限性。比如,双差法作为相对定位的一种,在地震台网分布密集的区域,有较好的定位效果。然而,在台站较少或地震与地震方位角覆盖较差的地区,双差法性能会变差[1]。在这种情况下,利用传统的定位方法无法得到精确的相对位置。本文所运用的基于尾波干涉(CWI)的相对定位方法适用于西北的现实条件,而且可以通过对单台的波形处理获得定位结果。
Frohlich和Pulliam[2]将单台地震定位的基本思路总结为利用三分量数据,将观测到的波形与合成波形进行匹配,从而确定震中距和震源深度;利用P波开始和P波结尾的偏振确定地震的方位角。国内外研究人员在此基础上设计了多种不同算法,并将其应用于区域小地震定位[3-5]和地震预警系统[6-7]等研究中。这些相关技术都是基于计算首波之间的走时差,波形其余部分(包括尾波)的信息被丢弃了。尾波指的是地震波形后期的多次散射波,它对地震源对之间的差异或传播介质的变化极为敏感。为此,利用与已知震中位置地震的波形互相关进行单台地震定位,这样则无需分别估计震中距和方位角[8-10]。Snieder[14-15]最早阐述了CWI如何利用尾波的互相关来估计地震之间的震源间距。Robinson等[11-13]利用尾波干涉方法对单台事件进行了定位,他们通过测量同一台站在某一变化发生前后所记录到的波形尾波的差异,来估计两种地震状态之间的差异。最后利用联合概率密度函数计算相对位置。Zhao等[16-17]提出的方法是在Robinson等人设计的CWI技术基础之上,改进了该方法。Robinson等[11]在确定一组事件的相对位置的目标函数时,在不同的台站通道上使用了平均主波长,但这样会导致定位过程的不准确性。为此,Zhao等[16]的概率密度函数在使用多个通道的数据的同时,引入了每个通道的实际主波长,也就是在计算联合概率密度函数时被该通道的实际主导波长归一化。最后通过求解一个优化问题来估计事件的位置。
2022年1月8日1点45分(北京时间)青海省海北州门源县发生MS6.9地震。如图1所示,由于门源台(MEY)距离余震区较近,大量的余震震级范围在MS0.0~MS2.0之间的地震事件仅被门源台一个地震台站所记录到(如图1),这与地震监测台网运用的至少3个以上台站震相到时的定位方法相比,观测报告无法给出准确的震中位置。为了对只有单台事件记录到的这种微小地震的震源位置进行估计,以获得与多台事件结果精度相近的估计结果,本文将尾波干涉的方法应用到该次地震的余震序列中,通过对多个余震序列进行分类,然后利用CWI技术来估计具有相似震源机制的事件群的震源间距,最后使用间距数据作为定位算法的输入来实现定位,定位算法通过不断的迭代来优化位置,使得目标函数值达到最小,从而得到最优的定位结果。
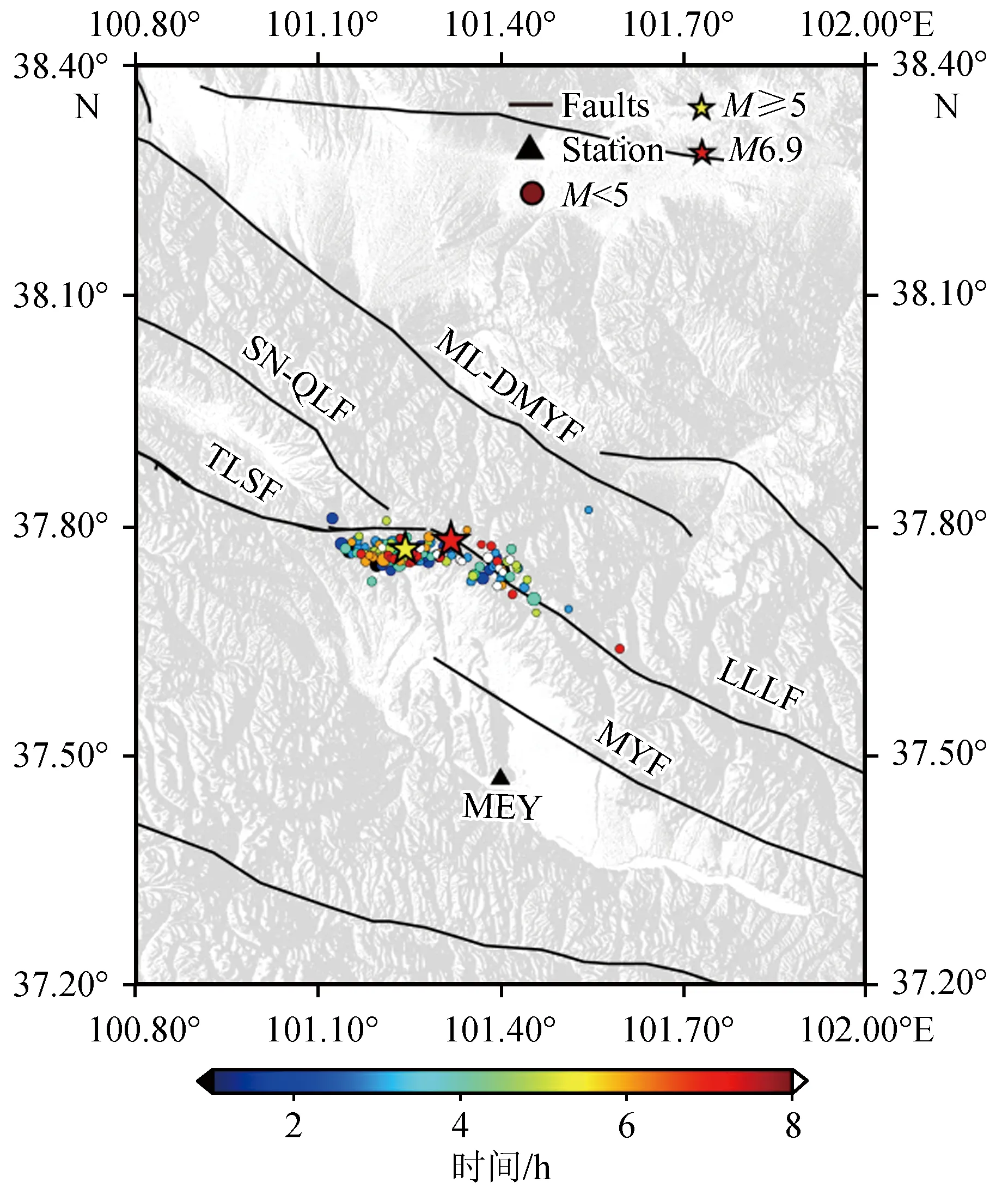
图1 地震台站和地震事件的位置分布图Fig.1 Distribution of seismic stations and events
1 计算方法
1.1 CWI方法介绍
不同类型的地震状态变化(速度变化、散射体位移、震源位移和震源机制变化)对地震尾波的影响是不同的,在这里,我们假设尾波的差异仅仅是由于不同地震事件震源位置的差异而引起的。在这种情况下,CWI通过每个地震台站通道记录到的两个地震尾波来估算一对事件之间的震源间隔,该理论基于散射波的路径和。
u1(t)=∑TAT(t),
(1)
式中:u1(t)为事件1的波形场,每个散射波的轨迹包括从源到遇到的第一个散射体的路径,以及之后的路径。对于接近于第一个事件且具有非常相似源机制的第二个事件,CWI假设每个传播路径上到达第一个散射体的路径会改变,但后续的路径不会改变,因为它取决于介质而不是源。由于随后的散射路径会造成与第一个散射体走时差的复杂混合,对于震源位置的微小变化,同一地震台记录的波形的主要差异发生在尾波到达时间。
u2(t)=∑TAT(t-τT),
(2)
式中:u2(t)为事件2的波形场、τT是由于源位置的不同,沿路径T向第一个散射体传播的波的走时差。如果我们假定两个源位置接近的源机制是相似的,那么这两个波形将是相似的。任何差异都可以由中心时间t和计算尾波时间窗序列的tw定义的一个时间窗的两个波形互相关来量化:
(3)
式中:2tw为时间窗长度;ts为时间扰动;t为时间窗的中间时刻。每个时间窗口内任意走时差τT的分布包含了震源间距δ的信息。Snieder[15]从相关系数的最大值Rmax中估计了走时差φτ的标准差,表明φτ与震源间距δ有关,本文是基于断层上的双力偶震源事件,从而有:
(4)
在不同时间窗到达的波沿着不同的路径传播,因此从每个时间窗得到的间距结果是独立的,它们的分布可以用来估计不确定性。研究还表明,不同台站通道的震源间距估计是高度一致的。
由于尾波被充分发散,一个时间窗包含了从不同方向离开震源的波,尾波的长度是有限制的。反过来,这就限制了公式(3)中使用的时间窗的数量和长度的选择,显然这两者之间存在权衡。
通过使用间距不确定性矩阵,系统地寻找窗口数、长度和开始时间的最优组合。对于每个站点通道的数据,计算一个三维间距不确定性矩阵,其中包括三个参数(窗口数、长度和开始时间)的所有可能组合。每个矩阵元素是通过计算Ωi,j=∑Nσi,j/N得到的,其中
(5)
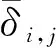
1.2 主要过程
本研究基于Zhao and Curtis[17]的方法,将CWI定位主要分为三个步骤:
(1) 计算互相关系数和分类
① 首先,计算所有可用事件对的平均最大互相关系数;
② 互相关系数反映了波形相似性,根据波形相似性采用Ottemoller[18]方法,将平均最大互相关系数按降序排列,把最大的两个作为第一个聚类的前两个事件,接着把与此相关联的其他事件依次添加到当前聚类,这样不断循环重复直到所有的事件被分类,便把一系列地震事件分成了不同的聚类。
(2) 用CWI技术估计震源间距
① 拾取初至点:对于在每个聚类中的每个通道记录的震群事件,交互式选取波形的初至震相到时。
② 寻找最优参数组合:通过调用CWI函数生成一个3维矩阵,来寻找所有事件对的窗口开始时间、长度和数量的最优组合,当三个参数组合的平均标准差最低时,即矩阵中元素的值最小时(每个元素是由相应聚类中相应通道记录的所有可用对的震源间距的平均标准差),为找到的最优组合。
③ 计算震源间距:以最优的窗口开始时间、窗口长度和数量,调用CWI函数计算相应聚类的相应通道所有事件对的源间距的均值和标准差。
(3) 计算震源位置
① 选择用于定位的事件对:它识别出了震源间距不适合用于定位算法的事件对,即根据经验阈值,其均值和或标准差过高或过低。
② 生成一组初始位置:首先在给定范围内创建一组事件的均匀分布。然后,对创建的事件重新排序,以确保震源间距的最小二乘残差(残差是每个事件对在创建的初始位置与CWI估计的间距差)。
(6)
图2为本文CWI定位的流程图。
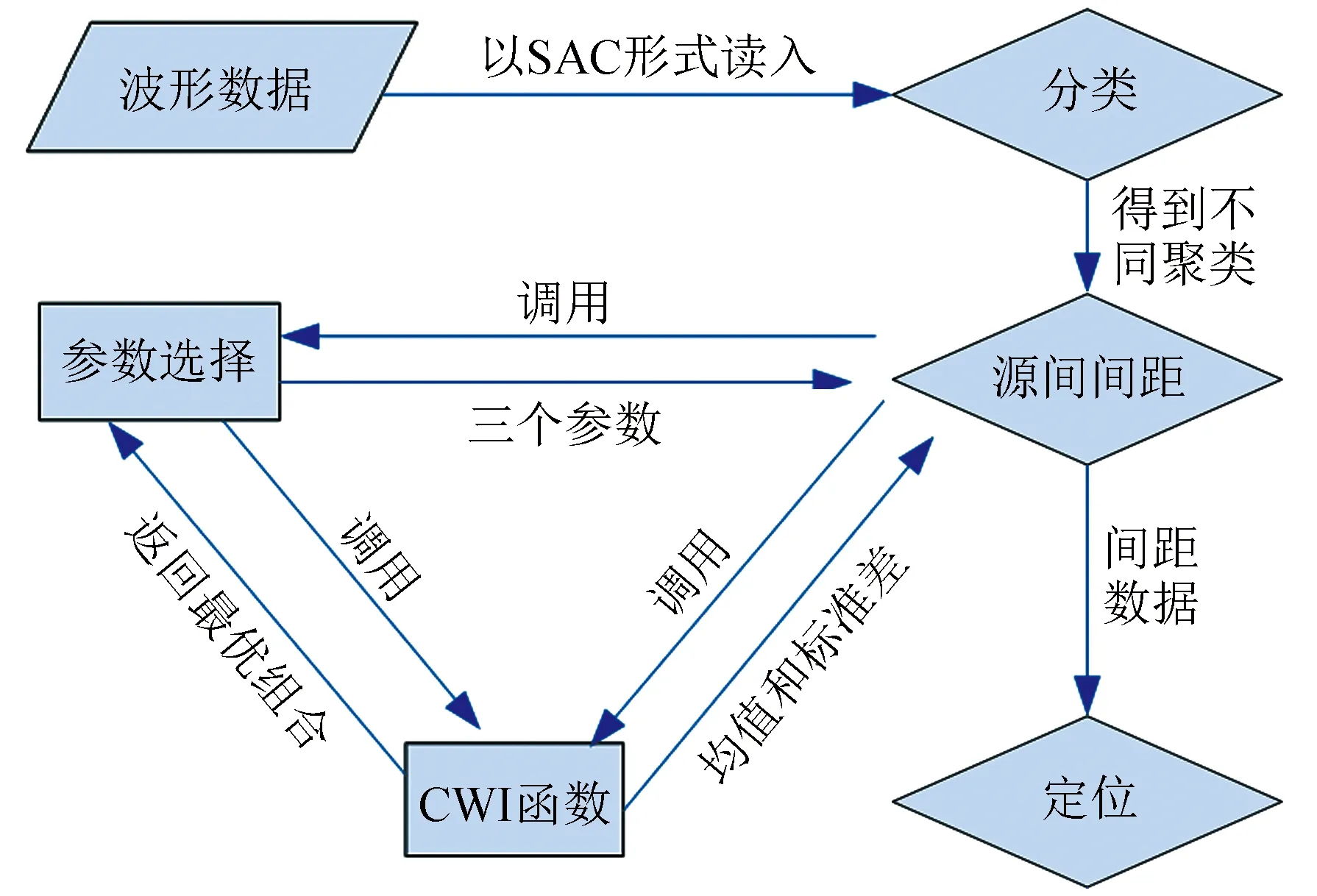
图2 CWI定位流程图Fig.2 The progress diagram of CWI location
2 定位结果
门源发生MS6.9地震后,余震序列活动频繁,门源台(MEY)作为该次地震记录到波形的首台,余震目录中含有大量门源台记录的单台事件,本文选取了震后8小时以内互相关系数大于0.6的101个单台事件,对其应用CWI方法进行了定位,对MEY台三个通道101个事件计算互相关系数,并进行分类,根据约束条件选择了36个事件3个通道,并分成了两类:聚类1中有30个事件,聚类2中有6个事件。图3是聚类1中30个事件的互相关系数矩阵,可见相似性最高的事件对的互相关系数可达0.97,相似性最低的可达0.67,图4分别是互相关系数最高和最低的事件对的波形对比图。

图3 聚类1中30个事件的互相关系数Fig.3 Correlation coefficient of 30 events in cluster 1
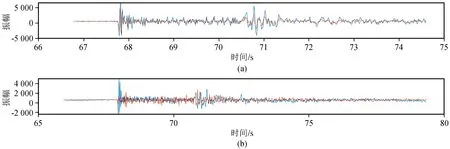
图4 互相关系数最高和最低的波形对比图Fig.4 A waveform comparison with the highest and lowest correlation coefficient
对于每个聚类中的每个通道的事件波形,我们使用间距不确定性矩阵(3D矩阵)找到CWI间距估计的窗口数、长度和开始时间的最优组合。例如,聚类1中的通道2得到的最低平均标准差是35.14 m,相应的最优组合为:时间窗开始时间为77 s,长度为1.0 m,数量为2个,其3D矩阵如图5所示。
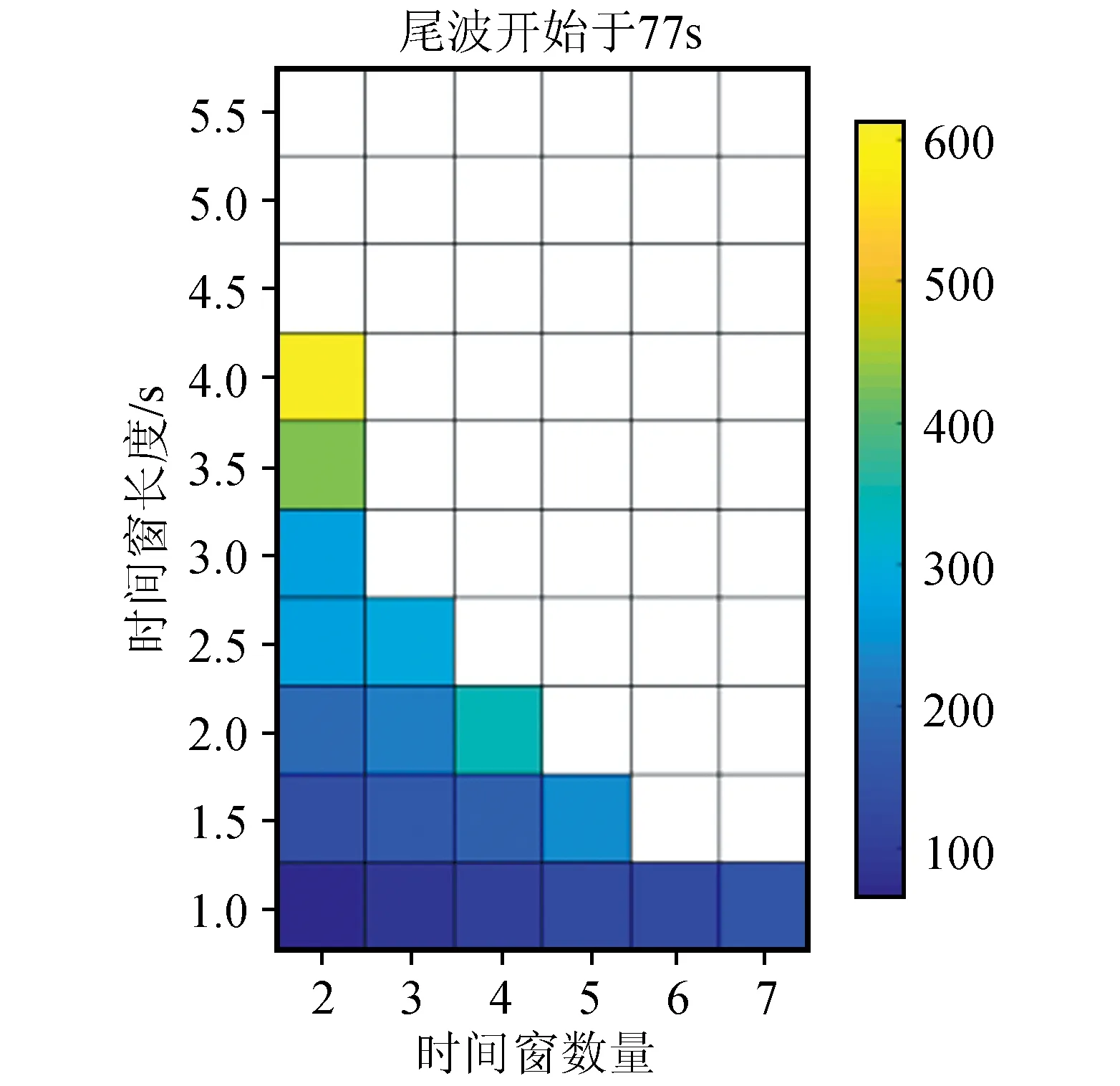
图5 时间窗参数选择的最优组合图Fig.5 Optimal combination of time window parameter selection
在最优参数的组合下,我们得到3个通道的间距值,最后将其作为定位程序的输入,在不同的初始位置的若干次迭代次后,最终得到的定位结果如图6(a)所示。图6(b),6(c)和6(d)分别为XY、XY和YZ平面的投影。
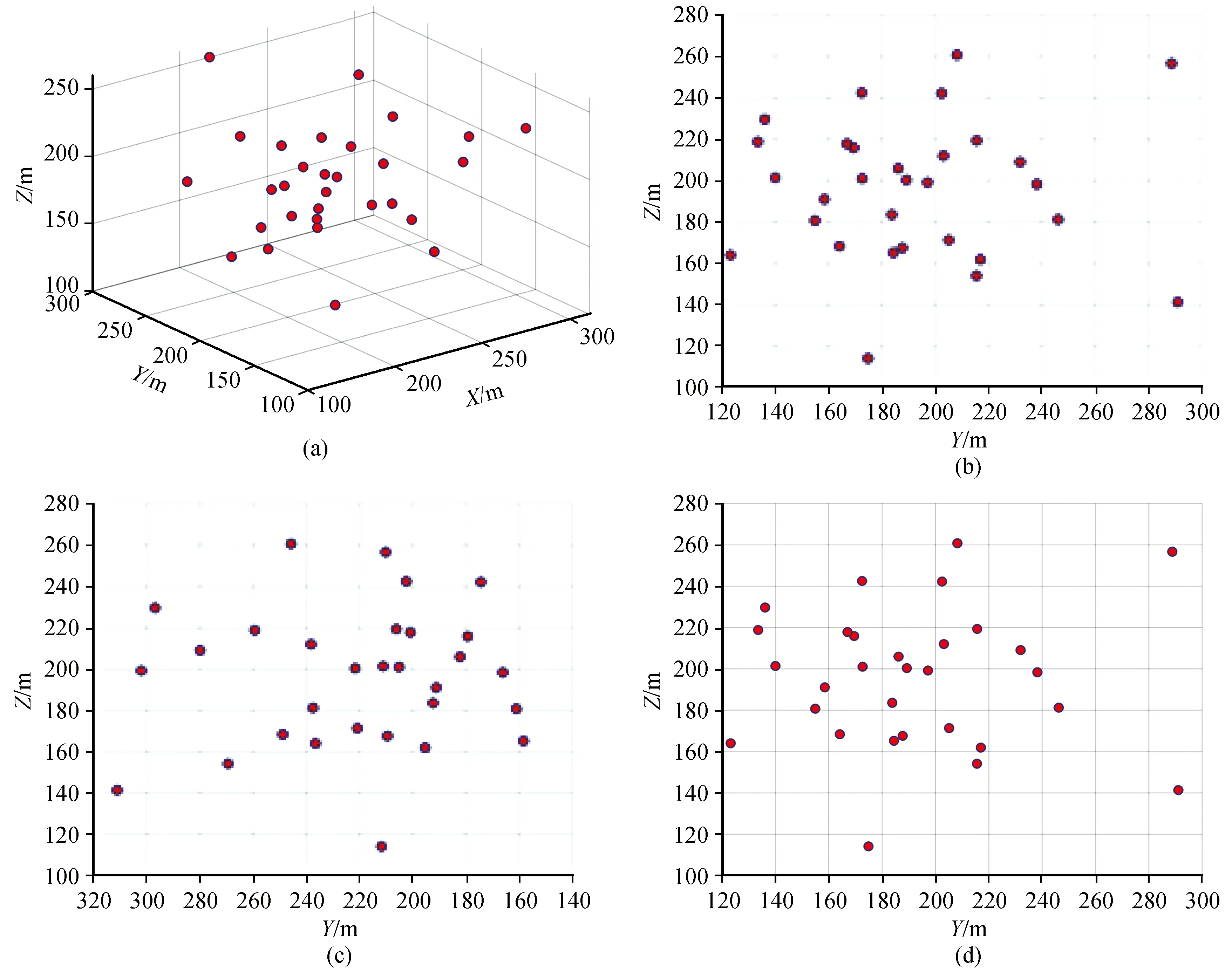
图6 定位图及其平面投影图Fig.6 Location map and its plane projection map
聚类1包含由30个事件组合的435个事件对,因此其目标函数L涉及435个成对似然函数的对数和(公式6),而聚类2包含6个事件,因此函数L涉及15个成对似然函数的对数和。为了更好地进行定位结果的分析,在下面的结果分析中只以聚类1中的30个事件为例。
本文使用了多个不同的初始位置来进行定位优化。所有不同初始化的迭代过程中目标函数值的变化如图7所示,不同颜色代表了不同初始位置的最小化过程,放大的小图显示了在每次优化开始和结束时目标函数的值是如何随迭代数变化的细节。一致性收敛水平表明,采用6种不同随机初始化位置得到的最小值接近全局最小;当L达到全局最小值时,就找到了相对震源位置。
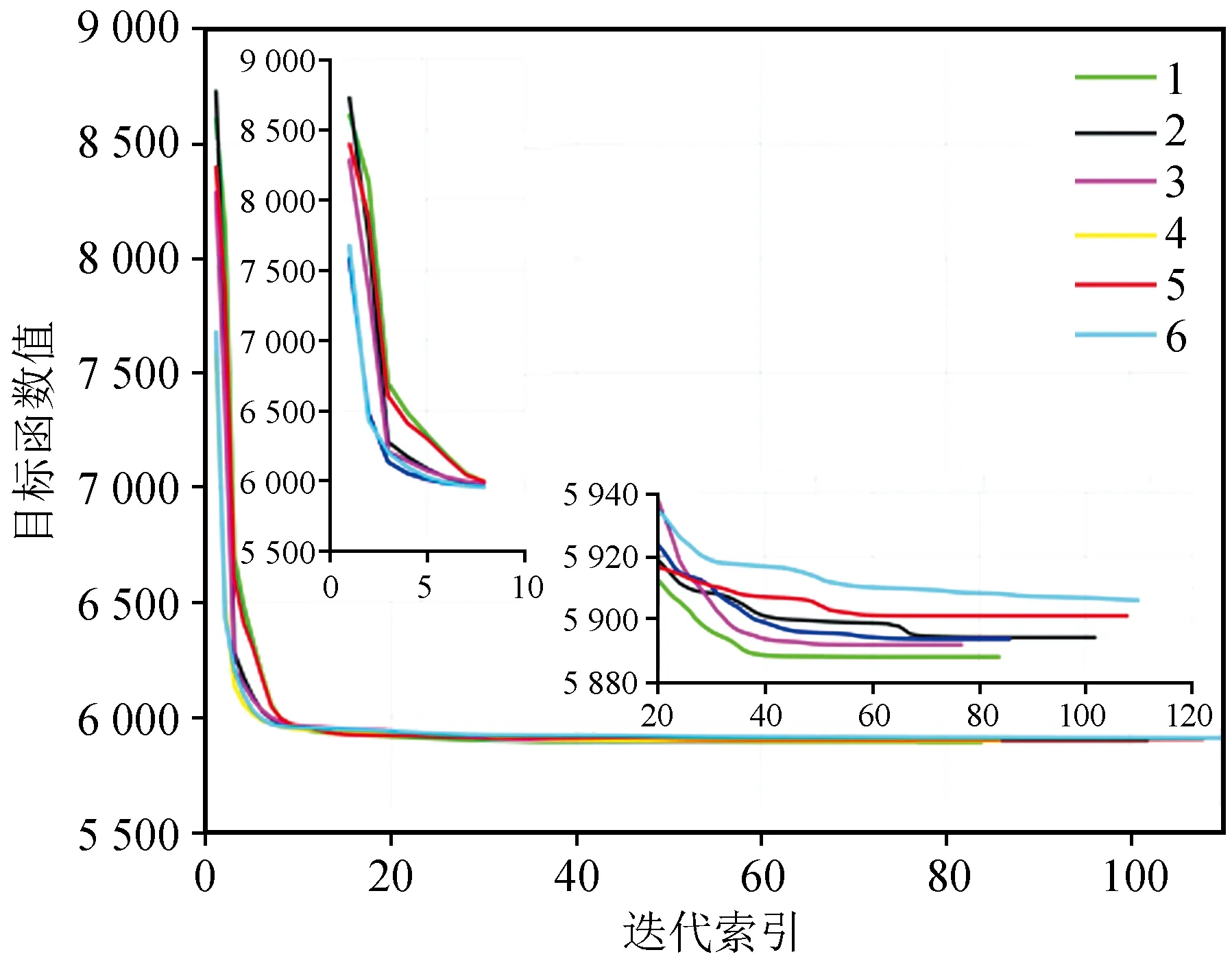
图7 目标函数迭代图Fig.7 Diagram of objective function iteration
3 结果分析与评估
图8为聚类1中30个事件定位结果之间的间距(紫色),与优化前三个通道(蓝色曲线为东西向、橙色为南北向和黄色为垂直向)的间距数据做了比较,可见优化后的事件位置间距要小于优化前的间距,这说明CWI震源定位技术能够给出可靠的相对位置估计。图9为聚类1中30个地震事件的定位结果所转化成的相应经纬度图。
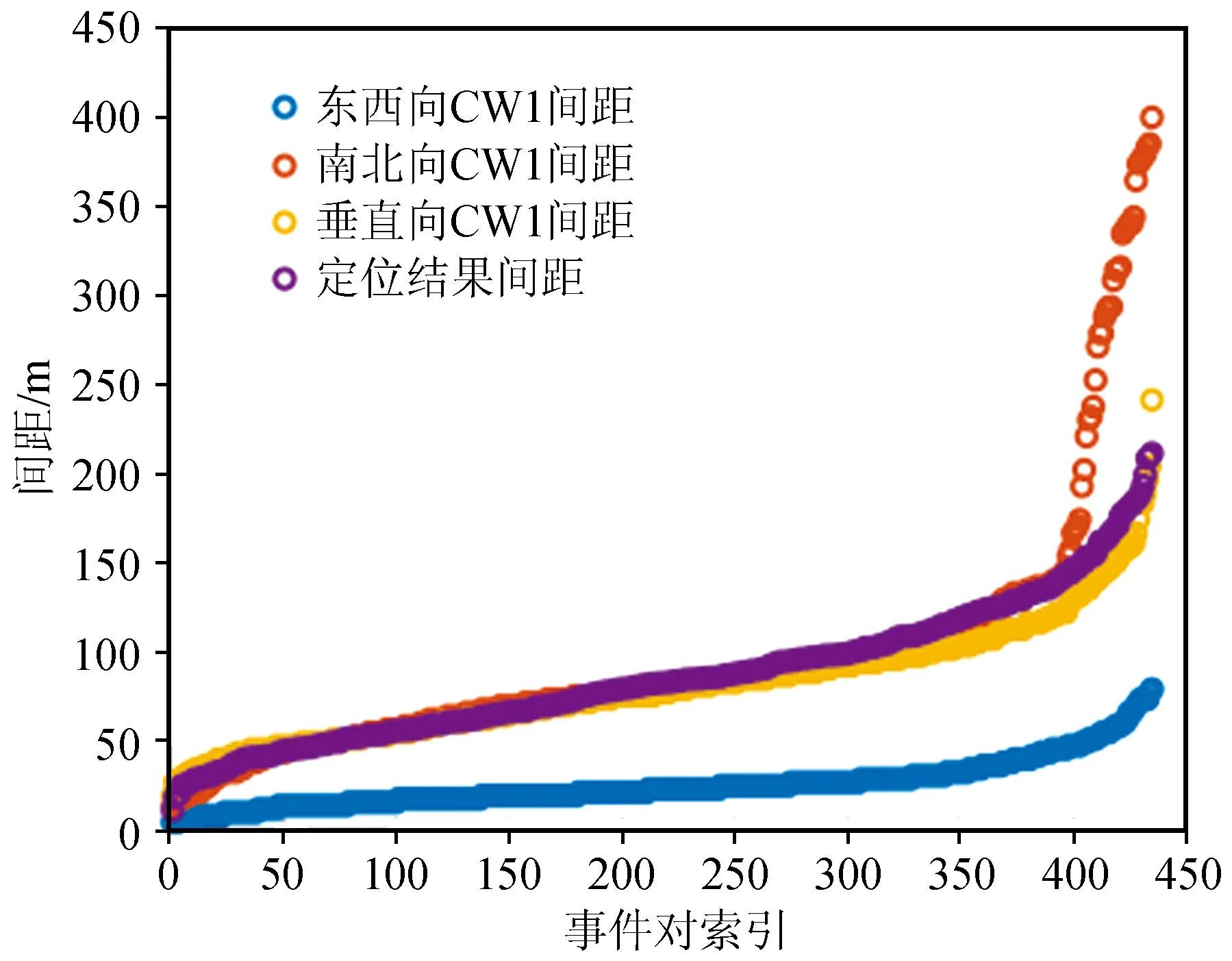
图8 震源间距比较图Fig.8 Comparison between hypocentral distance
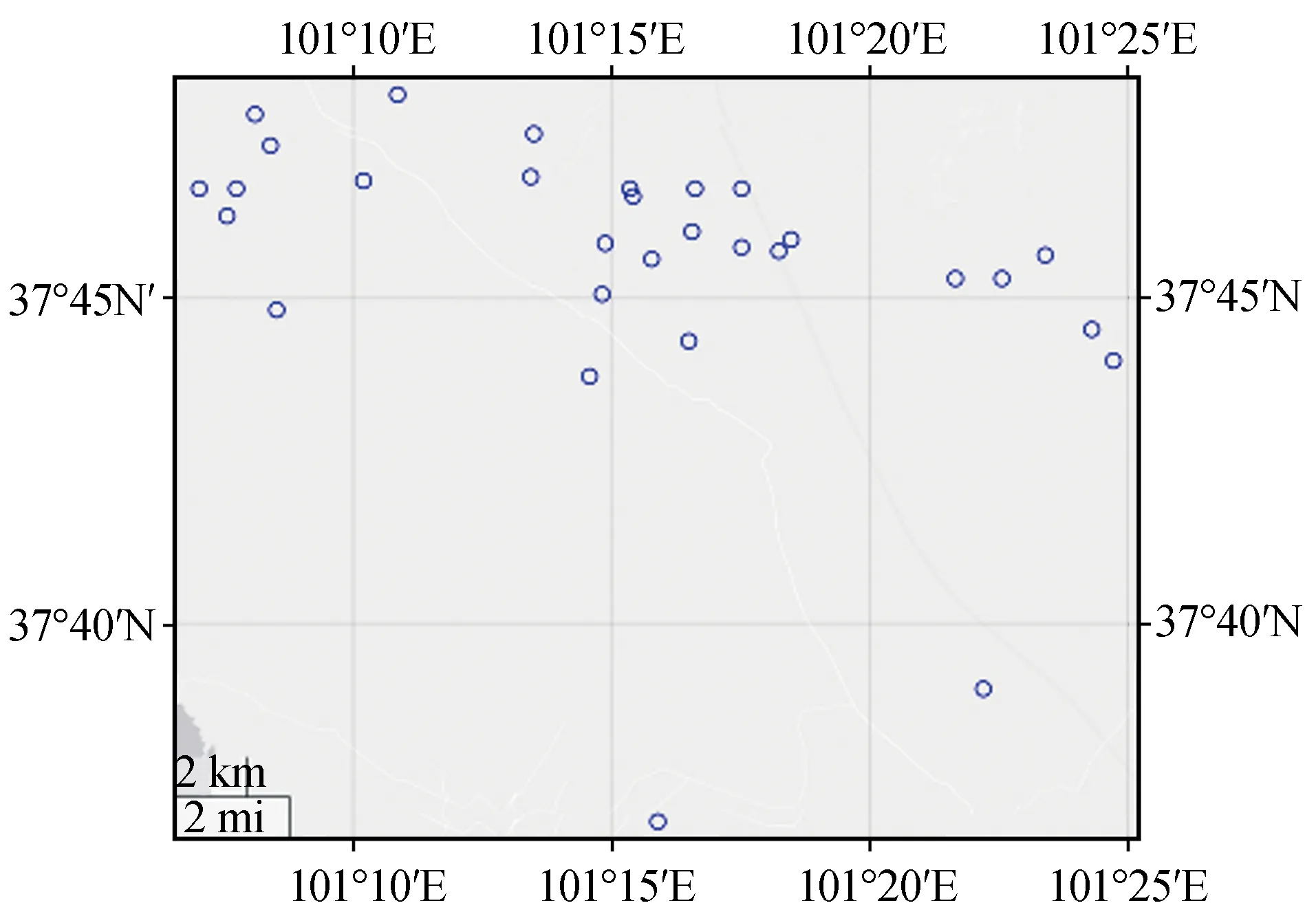
图9 经纬度图Fig.9 Latitude and longitude figure
为了进一步评估本文定位结果的可靠性,本文将CWI定位结果(实心黑色点)与定位输入(空心红色点)的初始位置做了比较,虚线代表他们之间的误差(如图10)。显然,CWI定位结果要明显比初始位置更聚集,这再次说明基于CWI定位的方法是精确的。
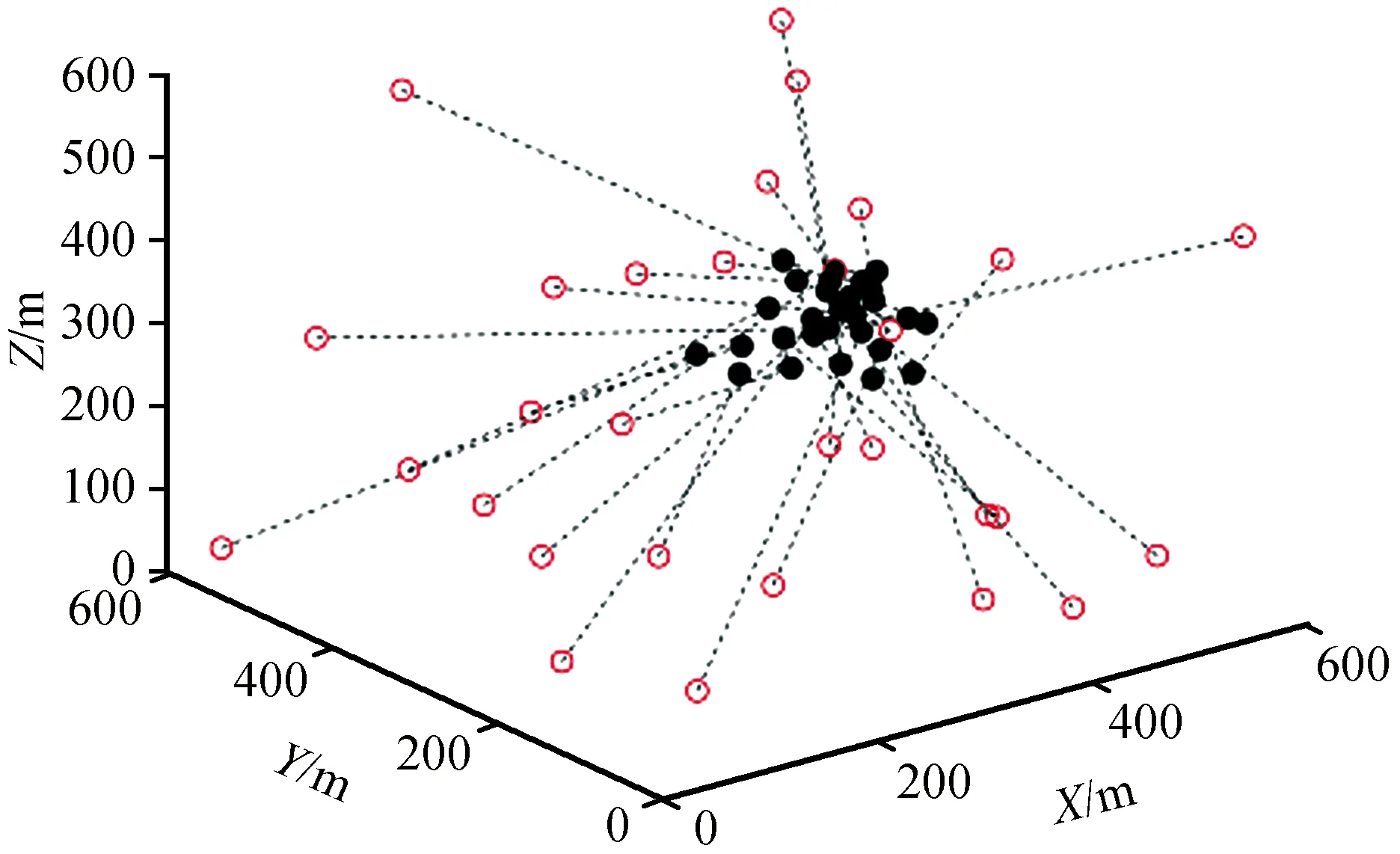
图10 结果比较图Fig.10 Location comparison
4 结论与讨论
本文通过利用尾波干涉的震源定位方法,对门源MS6.9地震余震单台事件进行了重定位,得到了相对可靠的定位结果。解决了单台事件定位的不准确性,补充了缺失的震源参数信息,提高了地震目录的完备性。同时也提高了利用含单台事件的地震目录进行分析研究结果的科学性和可靠性。这对于从余震序列中区分地震断层和辅助面,寻找地震事件的相对位置,研究地震相互作用和复发,监测应力状态和诱发(微)地震活动是至关重要的。此外,该方法还具有在西部稀疏台网应用的价值和优势。
值得注意的是,门源台距主震30 km左右,地震波的传播距离较远,导致波形相似度较低,用于计算的地震事件数较少,并可使用更加接近断层的流动台站等观测数据来对序列微震进行定位,从而进一步完备地震目录[19]。
致谢:感谢甘肃测震站网提供的地震波形资料,两位审稿专家提出的建设性意见对本文帮助很大,在此一并感谢!
