加权整体最小二乘坐标匹配算法在机场道面测量中的应用

戴中东孟 良高永攀项 伟

1空军研究院工程设计研究所，北京，100068

2北京特种工程设计研究院，北京，100028

机场道面高程图（也称为板角高程图）测量一般在机场改扩建设计前或者机场建设竣工后进行。板角高程测量精度至毫米［1］，一般尾数为估读，且板角点相对临近水准点高程中误差不大于5 mm，极限误差不大于1 cm，因此可认为，板角高程测量的精度要求优于1 cm。传统的测量方法将平面数据和高程数据分开进行采集，然后一一对应合并（一个机场大概3万个数据），过程繁琐，工作效率低下，且很容易出现错误。地面三维激光扫描仪（terrestrial laser scanner，TLS）发展已经30多年，特别是近10年来，精度高、测速快的扫描仪已经逐渐走进各个应用领域［2］，比如工程测量［3］、文物保护［4］、工业测量［5］、交通道路测量［6-8］等，极大提高了工作效率。

但根据机场道面高程测量中的精度要求，采用常规扫描仪流程，主要存在以下3个主要问题：一是靶标控制点的高程精度要足够高，且测量过程中需要尽量减少“量高误差”；二是由于道面测量对平面精度和高程精度要求不一致，特别是扫描仪没有整平装置时，平面坐标误差会影响高程匹配的精度，且配套软件没有对权值进行设定；三是由于机场周边地势平坦，且无连续制高点，距离仪器越远，道面测量点的反射角就越小，大于70 m几乎就没有回波数据，这样就使得相邻测站的距离不能太大。因此采用常规的三维扫描仪测量方法，不仅效率低，而且也不能满足厘米级以内的高程精度。

本文首先分析了使用加权整体最小二乘［9-11］进行坐标匹配转换的算法，该算法公式经过推导和向量化后，采用LM（Levenberg-Marquardt）算法求出最优转换参数，并对目标坐标和测站坐标的误差来源进行分析，确定了权值；其次，为了减少靶标量高误差和提高地面回波率，设计了一种控制点布设方案和测量方法；最后，通过实例数据的分析和比较，得出结论。

1 坐标匹配算法和权值的确定

1.1 加权整体最小二乘法坐标匹配算法

TLS外业测量时采用的是测站坐标系统，而目标坐标为测图时采用的坐标系统，两者之间需要转换。由于测站坐标和目标坐标均含有随机误差，直接采用经典最小二乘法求解转换参数时，求出的结果会有偏差［12］。因此需要使用变量中存在误差的EIV（errors-in variables）模型，求出最优估计参数解。从测站坐标到目标坐标系统EIV模型公式为：

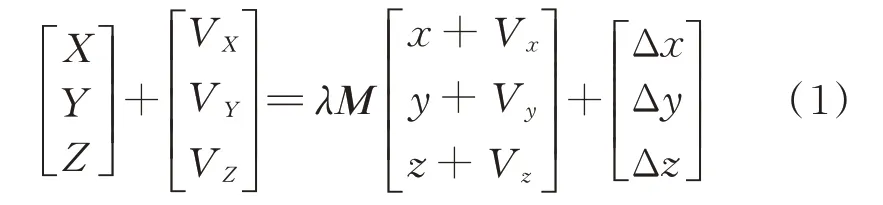
式中，[XY Z]T为目标坐标向量；[Vx Vy Vz]T为目标坐标误差向量；[x y z]T表示测站坐标向量；[vx vy vz]T为测站坐标 误差向 量，[ΔxΔyΔz]T为平移参数向量；λ代表尺度缩放参数，TLS的坐标转换中，一般认为λ等于1；M为3个旋转角组成的旋转矩阵。

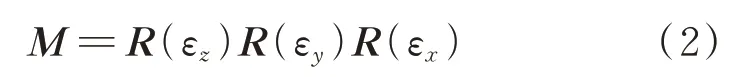
根据式（1）、式（2）可以得出：

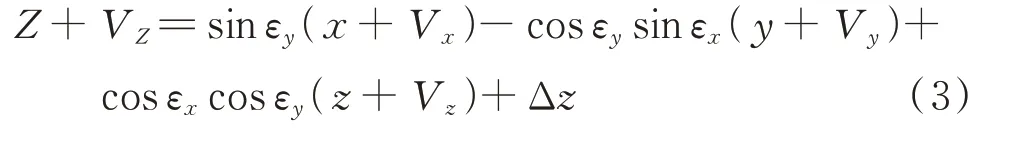
由式（3）可以看出，在仪器整平的情况下，εx、εy为小角度，sinεx、sinεy也为极小值，cosεx、cosεy接近1，这时，目标坐标高程主要与测站坐标的z方向坐标分量、误差、平移参数相关。但是，TLS一般没有整平装置，这时，目标坐标高程与测站3个坐标分量以及误差、平移参数均相关。

由式（1）、式（2）可以看出旋转参数和系数矩阵呈非线性关系，无法直接使用整体最小二乘算法求解，一般将式（1）转换成线性化的模型求解，但该方法仅仅适合于两套坐标系间的旋转角较小时的转换，若旋转角较大时，模型误差会很大，甚至完全得不到正确的结果［13，14］。

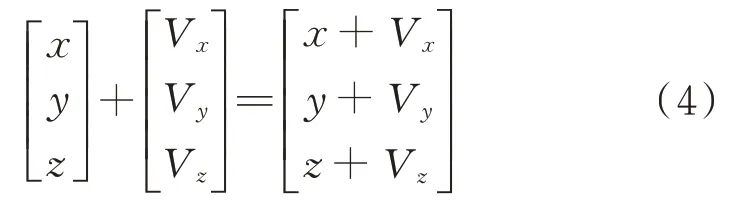
将式（1）和式（4）联立，坐标转换模型转化为非线性GM模型：

式中，l为式（1）和式（4）中目标坐标和测站坐标的向量化；V为误差的向量化。假设A为测站坐标系统的n个坐标，βc为6个坐标转换参数，vec表示逐行向量化，则变量参数β可表示为：

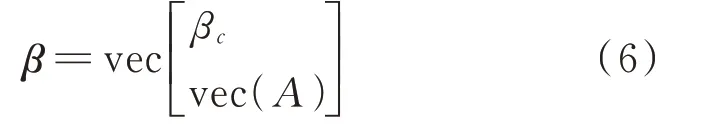
其中，f(β)为式（1）和式（4）联立后的方程的右半部分。

经过向量化变化后，式（5）转换为非线性方程的最优化问题，加权整体最小二乘的最优估计的函数可表示为：

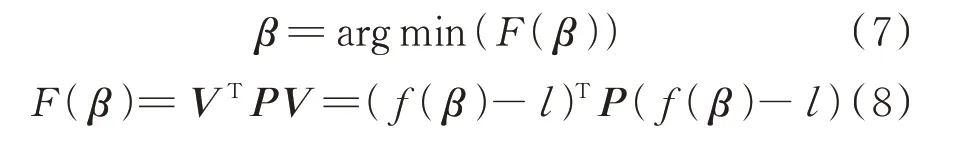
式中，P表示权值。

对于非线性方程的最优化问题，常见的方法有梯度法和高斯牛顿法。梯度法主要从负梯度方向进行迭代搜索，并最终找到极小值，该方法开始时下降较快，但靠近极小值时收敛速度很慢。高斯牛顿法中由雅克比（Jacobian）矩阵近似计算海森（Hessian）矩阵，避免了直接计算海森矩阵的复杂性，收敛速度快，但是该算法对初始值较敏感，容易陷入局部极小值。LM算法引入阻尼因子［15］，每次迭代时调节阻尼因子μ，使算法介于梯度法和高斯牛顿法之间，能有效克服常见缺点。对于本文的加权非线性方程的求解中，在梯度向量G和海森矩阵H更新时需要加入权值项。

每一次迭代时，h表示β值的更新值：

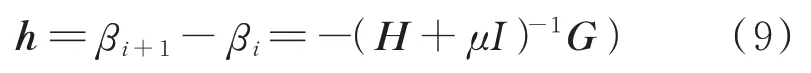
当梯度的无穷范数小于预定的一个极小值ε1，或者通过更新值h和变量参数的2-范数进行比较，当小于变量参数的一个极小比例ε2时，程序找到非线性最小二乘的最优解β，由式（6）可知，解的前6个值就是旋转角和平移量参数。本文中ε1、ε2均设置为1×10-10。

1.2 权值的确定

机场道面很平整，横坡和纵坡最大也不超过2%［16］，即平面偏差5 cm，对高程影响也就1 mm。为了保证高精度的道面高程测量成果，同时又提高效率。靶标控制点的平面坐标使用GPS-RTK采集，高程则使用二等水准进行测量。道面测量采用RIEGL VZ-1000三维激光扫描仪（角度分辨率1.8″，小于100 m距离的测距精度5 mm），是一款高密度、高精度、高效率的扫描设备。

目标坐标系统下靶标点的测量误差分为平面和高程两个部分。由于平面坐标由GPS-RTK采集，有固定误差，对中杆手握对中以及其他因素引起的偶然误差，要准确计算每一个点的平面误差比较困难。由于机场环境空旷，高度角大于15°的卫星一般都能接收到信号，本文计算中统一设置为2.1 cm中误差（两个坐标分量都是1.5 cm的中误差）。由于电子水准仪的普遍应用，水准测量的效率和精度都得到了很大提高，有的仪器甚至已经达到了0.2 mm/km的高程中误差，本案例的控制点采用二等水准测量，平差后高程中误差为0.6 mm，加上放置靶标的误差后，统一设置为2 mm。

测站坐标系统是扫描仪外业测量时采用的坐标系统，靶标位置在该系统的误差包括两部分：一是仪器的测量误差，另一个是靶标识别的误差。其中在测站坐标系统下，如图1所示，仪器的观测量为：水平角α、垂直角θ、以及斜距S。则仪器的测量中误差在3个方向上分别为［17］：

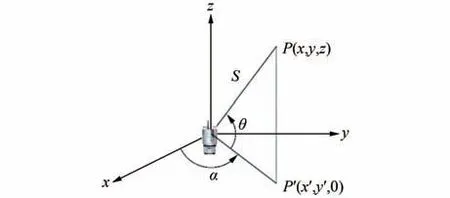
图1 测站坐标示意图Fig.1 Schematic Diagram of Station Coordinate

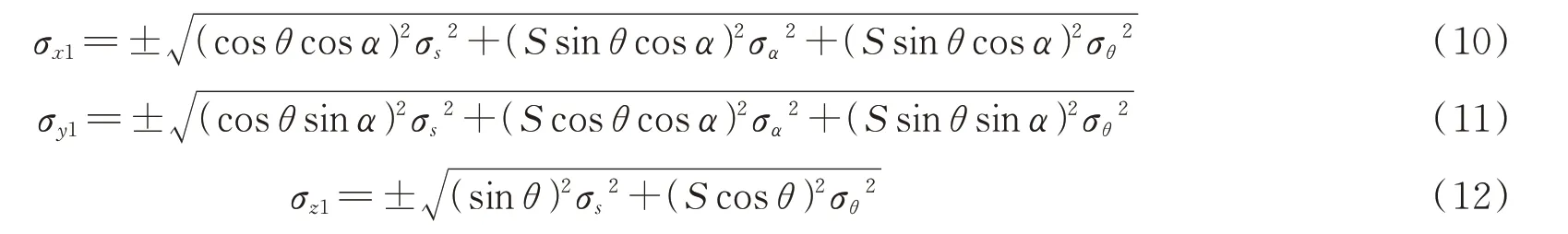
靶标识别误差主要和靶标上的点云密度有关，扫描仪道面扫描时使用的是6 cm×6 cm的平面靶标，放置在10 m位置时约有6 000个点，点间距约为0.8 mm；放置在120 m位置时就只有200个点，点间距约为4.2 mm。虽然扫描仪没有对中和整平装置，但是一般情况下，扫描仪在测量时基本保持水平，本文中将靶标识别误差设定为点间距σxy≈σz2≈±d，其中x、y代表水平方向，即使用随机软件RiSCAN中的点云个数求出各靶标的点间距后，将水平方向的误差、垂直方向的误差设定为点间距。

如图2所示，x、y、z方向的识别误差分别为：

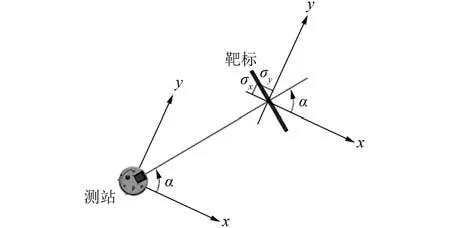
图2 靶标误差平面投影Fig.2 Plane Projection of Target Error

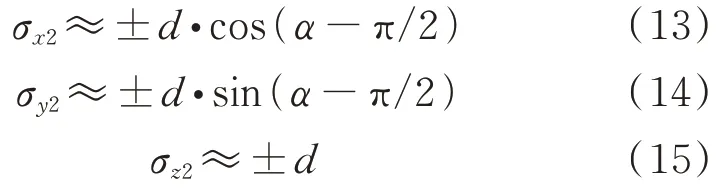
测站坐标的3个方向总误差分别为：

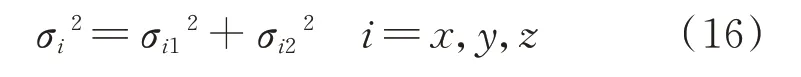
目标坐标和测站坐标的误差都计算出来后，就可以对整体最小二乘的权值进行确定，pi=σ02/σi2，其中σ02可以选定为σi2的最大值。权矩阵可表示为：

式中，diag代表生成对角化矩阵的符号，即将向量的成员作为矩阵对角线上的元素。这样，权值即可确定。

2 实例数据采集和分析

2.1 数据的获取

机场道面周边无连续制高点，数据采集时使用专用脚架提高仪器的架设高度。普通脚架只能把仪器高度架设到1.5～1.7 m，使用工业级的专用脚架，把仪器高度架设到2.6～3.0 m。提高仪器高度，不仅可以测量得更远，提高效率；同时，由于反射角的增大，反射率增加，也提高了测量精度。

如图3所示，将靶标贴在平整长方体一面，直接将靶标的投影中心对准控制点平面中心，放置在控制点的最高处，靶标面朝向仪器中心，优点在于避免了过大的对中误差和量高误差。需要注意的是，匹配该靶标点的高程应该为控制点高程加上3 cm（平面靶标的一半尺寸），平面坐标不变。

图3 架设仪器和放置靶标Fig.3 Instrument Erection and Target Placement

靶标布设时要分布均匀，且避免靶标点共线和共面的情况，防止坐标匹配时无穷多解的情况。待匹配的靶标点布设在道面两边线外的助航灯基座螺母上，航灯的间距约为50 m，跑道宽度一般和机场等级有关，多数为45～60 m，如图4所示。一个测站可以扫描12个靶标，其中8个在本测站扫描范围内，另外4个在范围外附近。机场道面测量时，将扫描仪架设在跑道中心线上，为便于相邻测站的结果进行检核，使后一测站的点云和前一测站有重叠，使测站重叠区域离相邻测站的最大距离在100 m左右。

图4 靶标点布设示意图Fig.4 Schematic Diagram of Target Placement

2.2 分析和比较

实验1：采用8种坐标匹配方案，比较各种方案的匹配精度，具体匹配方案和匹配精度如表1、表2所示。

表1 坐标匹配方案Tab.1 Coordinate Matching Scheme

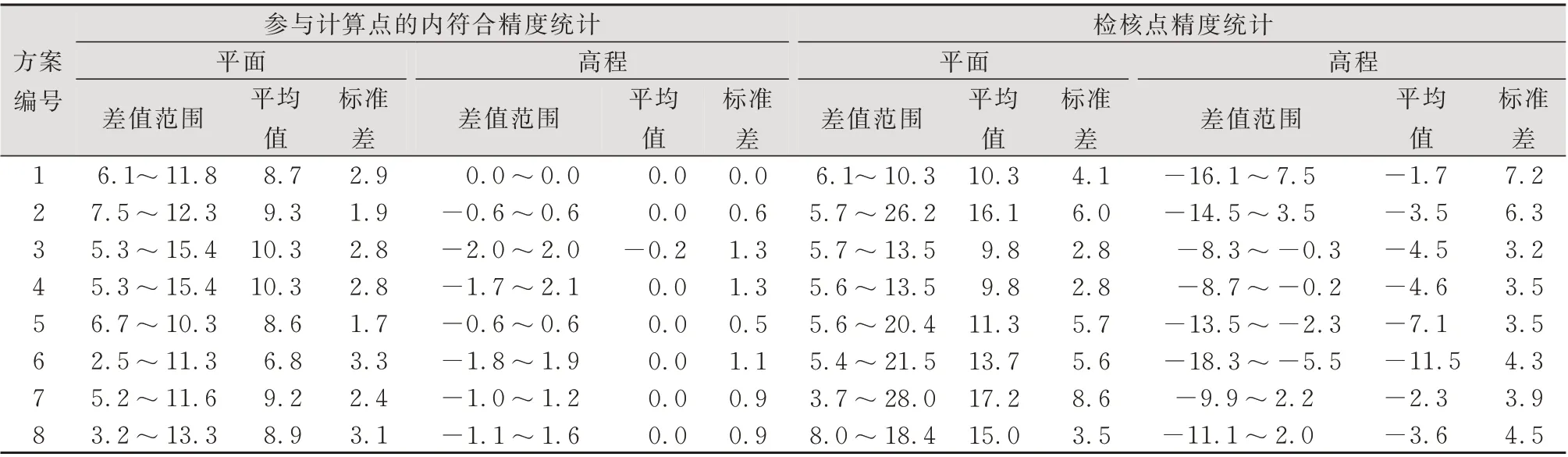
表2 坐标匹配精度统计比较/mmTab.2 Statistical Comparison of Coordinate Matching Precision/mm

在表2中，方案1只有必要的3个点参与参数计算，没有多余点，无法平差，虽然内符合精度很高，但从检核点的精度统计可以看出高程的差值范围很大，标准差最大，证实了采用本文算法的必要性。

由于EIV模型把误差作为变量进行平差，考虑了目标坐标系统中存在误差，所以在参与计算点的内符合精度统计中，方案3和4的高程差值标准差比较大，但是检核点的高程标准差最小。方案3的检核点高程精度最高，平面精度符合实际RTK测量的情况，因此8个临近的点的参数估计最稳定。方案4的整体精度和方案3相近，也符合式（3）的εx、εy为小角度的情况。

方案5～方案8为匹配点在一侧的情况，另一侧的检核点高程出现较大的偏差，这是由于靶标分布不均匀造成的，这个结论也符合文献［18］的结论。方案6、方案8使用了两个近130 m的靶标，靶标的分辨率过低引起这两个方案的高程整体精度不如方案5和方案7。

实验2：TLS多数没有整平和对中系统，仪器的坐标平面和目标坐标平面产生夹角在所难免，主要体现在以坐标x轴和y轴发生旋转，本文假设产生0～10°的旋转，使用测站周边的8个点作为参数计算点，剩下的4个点作为检核点，对不加权和加权进行比较。

如图5所示，等权的情况下，参与计算点的内符合高程转换差值的标准差在1.3～1.8 mm之间，检核点的高程转换差值的标准差在3.5～5.5 mm之间。不论是内符合还是检核点的精度，都随着旋转角的加大而增加，最大的情况出现在x轴和y轴同时旋转10°的情况。可以看出，在2°旋转角的范围内，高程的转换误差还算稳定，也就是旋转角度较小的情况。

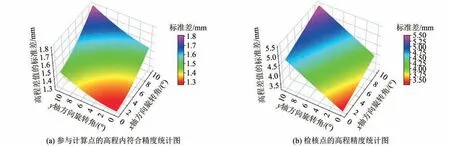
图5 等权情况下的精度统计图Fig.5 Precision Statistical Diagram Under Equal Weight

如图6所示，加权的情况下，参与计算点的高程差值的标准差非常平稳，保持在1.3 mm，检核点的转换差值标准差也较稳定，保持在3.5～3.7 mm。对比图5、图6可以看出，符合式（3）的推导，即没有整平装置时，目标坐标高程和测站3个坐标分量以及误差、平移参数都相关的结论。加权的情况下保持着等权差值的最小值，并非常稳定，说明了该算法具有通用性和强壮性。

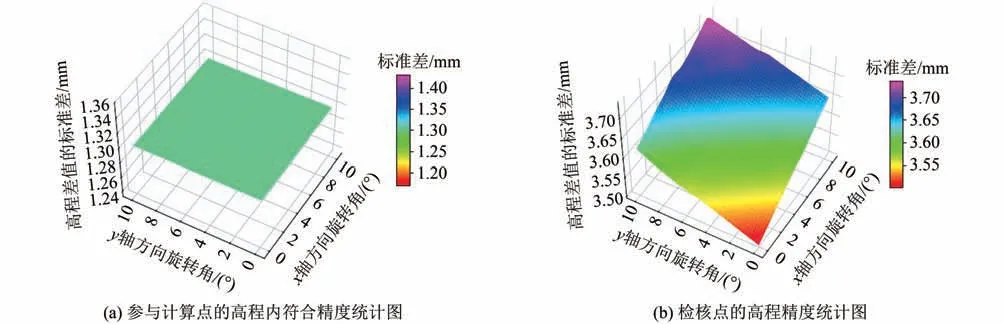
图6 加权情况下的精度统计图Fig.6 Precision Statistical Diagram Under Weighted

由于两站重叠部分的点云距离两测站都最远，该处的扫描精度最低，外业时使用常规的方法（水准仪）抽样测量了几个测站重叠部分的高程，共计119个点，与TLS点云过滤分类后的结果进行比较得出，差值范围在-12.1～8.7 mm之间，大于1 cm差值的点只有3个，且都位于道面边缘处，是源于该处有覆土或者植被的影响，所有差值的均值为2.2 mm，差值标准差为±4.6 mm，也就是精度优于1 cm，可以认为本文的方法完全能满足机场道面测量的要求。

3 结束语

本文分析了加权整体最小二乘算法的理论和实现方法，并且对TLS的目标坐标系统和测站坐标系统误差进行了分析确定，并针对某机场实测的数据进行计算比较，得出结论：由于测量效率的需要，匹配点的目标坐标采用不同的设备采集，这样就需要使用加权整体最小二乘法进行转换参数的求解，这样才能得到最优的参数估计，并有效减小三维激光扫描仪不能整平带来的误差。同时在高精度的道面高程测量的应用中，采用此方法可以有效的提高高程精度，最终达到优于1 cm的高程精度要求。

传统方式测量一个机场的板角高程需要4人（一名观测员、一名记录员、两名跑尺员），15 d左右才能完成工作。采用本文方法只需要3人（两名仪器操作员，一名靶标摆设人员），3 d就可完成同样工作。无论从人力需求上还是工作效率上都明显得到了提高，而且避免了传统方式平面和高程分开采集，最后融合易产生的错误。本文方法对于其他一些对单一方向有高精度要求的测量工程，如道路、特殊构件的平整度测量等，都有很好的借鉴作用。