基于激光基准的矿山井筒变形监测技术研究

陈 梦独知行张 涛李晋东

1山东科技大学测绘与空间信息学院，山东 青岛，266590

2武汉大学测绘学院，湖北 武汉，430079

3海军工程大学导航工程系，湖北 武汉，430043

矿山立井是矿业生产的主要结构，承担着运输、通风、通信等重要功能。为满足日益巨大的矿产需求，矿业开采向着地下更深处延伸，井筒的深度不断增加。由于使用过程长期受外力作用，加之地质条件影响，井筒会出现变形，因而对其进行变形监测具有重要意义［1］。

根据测量工具和监测原理的不同，将井筒变形监测方法分为基准线法和智能监测技术。基准线法，一般利用钢丝或激光垂准仪建立观测基准，测量井壁特征点坐标，确定各个监测横断面之间的相对位置关系，从而分析井筒变形状态［2］。智能监测技术，即不需要建立基准线的实时监测技术，比如基于传感器的自动报警系统，通过在井壁安装温度、位移、应力等传感器，实时动态监测井筒壁的形变数据，还有利用摄影测量方式，建立井筒三维影像，获得变形情况［3，4］。鉴于激光基准具有操作简单、测量精度高、受环境影响小等优势，本文将重点研究基于激光基准的井筒变形监测技术，以提高该方法的适用性。

1 激光基准的建立与传递

实施井筒变形监测工作，首先需在各个监测面上选取、标记变形特征点，利用特制设备将两台激光垂准仪固定安装在井筒内的横向支撑梁上，接着测量人员随罐笼升降，准确测出激光投点与特征点的水平距离。选设特征点、安置激光垂准仪、测量平距即建立了激光基准。

目前较为常用的激光垂准仪是苏州一光生产的JC100和DZJ2系列，向上、向下都能发射激光，可达150～200 m的射程，并具有相当高的垂直精度，满足井筒监测精度要求。由于激光发散，一次激光基准难以完成较深井筒的整个测量工作，需要进行基准传递。

在井筒更深处，重置两台激光垂准仪，选取上一基准的一层或两层横断面作为公共监测面，测量出新基准下水平距离，反算新激光点的坐标，以此建立起新的激光基准。激光基准建立与传递如图1所示。

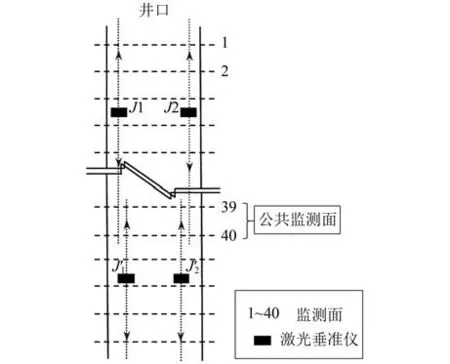
图1 激光基准的建立与传递Fig.1 The Establishment and Transmission of Laser Datum

鉴于井筒凿井技术与装备难易程度的配备情况，将井筒按深度划分为5类，超过1 200 m的是超深井和特深井［5］。但我国广泛采用的是小于1 200 m的立井井筒，所以进行变形监测时最多需要两次基准传递，即可完成我国大多数井筒的变形监测工作。

2 井壁特征点的计算

每一层监测面上的井壁特征点坐标实质是根据测边交会原理得到，特征点示意图如图2所示。

图2 井壁特征点示意图Fig.2 Schematic Diagram of Borehole Wall Feature Points

图2中，X-1、X-2…为井壁特征点，其中X表示监测面的层号，1、2表示该监测面上特征点的点号；J1、J2为激光投点，S为激光点间平距；d1、d2为测得的激光点到特征点的平距。

利用激光投点坐标J1(xJ1，yJ1）、J2(xJ2，yJ2），按测边交会公式，计算井壁特征点坐标为：

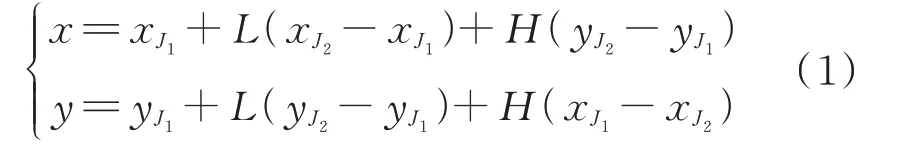
为了分析井筒整体变形情况，需对各层监测面进行圆心拟合，拟合方法可采用最小二乘法，充分研究其相对位置关系。

3 新激光点坐标计算方法

准确计算出新激光点坐标能有效提高基准传递的精度，常用的计算方法有测边交会法，本文在此基础上提出了多距离交会法和平面参数转换法。

3.1 测边交会法

在公共监测层上，通过旧激光基准可以获得该层变形特征点的坐标，利用测得的特征点到新激光投点的平距，任意两个特征点按测边交会的原理即可计算出一组新激光投点坐标，最后取多组坐标的平均值作为终值。测边交会法较为直接，但任意两个特征点都能计算出一组坐标值，具有较大计算量，同时易受交会误差影响，为保证计算正确性，需对多组计算坐标值进行筛选，选择偏差值较小的坐标值参与平均计算。

3.2 多距离交会法

多距离交会法在测边交会法基础上提出，将某层公共监测面上所有特征点整体参与计算，根据激光点到特征点的平距建立误差方程，按间接平差公式计算激光投点的坐标［6］，特征点示意图如图3所示。多距离交会法相对减少了工作量，不用考虑特征点位置关系，最小二乘约束能对测量误差和交会误差起到一定控制作用。

图3中，J′1、J′2为新基准激光投点；d1～d6为公共监测面上新激光点到特征点的平距。

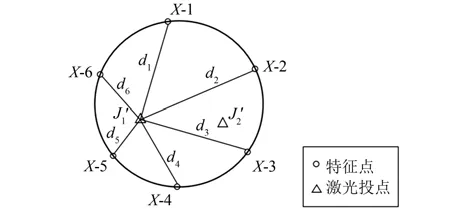
图3 多距离交会法示意图Fig.3 Schematic Diagram of Multiple Distance Intersection Method

3.3 平面参数转换法

以新激光投点相对位置关系，建立独立坐标系x′o′y′，即以J′1为坐标原点o′，J′1J′2直线方向为y′，垂直方向为x′方向建立平面直角坐标系，示意图如图4所示。按测边交会公式，可以计算出公共监测面上各变形特征点的独立坐标系下坐标(x′i i，y′i），对应其旧激光基准下地面坐标(xi，yi），根据平面四参数模型计算坐标参数，即可将新基准下特征点和激光点独立坐标转换成地面坐标系统中，完成新旧基准坐标系统的统一［7］。平面参数转换法是将新、旧基准测点的坐标独立计算，通过四参数转换模型纳入到同一坐标系下，一定程度上减少了旧基准测点误差对新基准测点坐标的影响。

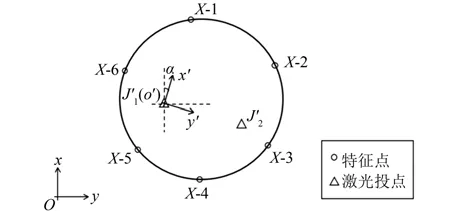
图4 平面参数转换法示意图Fig.4 Schematic Diagram of Plane Coefficient Transformation Method

4 实例分析

江苏大屯某煤矿副井，深度约450 m，设计半径4 m，由于建设年代久远，井壁多处出现剥落、凸起和凹陷现象，罐道垂直精度降低，为进一步排查安全隐患，对其开展了基于激光基准的井筒变形监测工作，具体实施如下：

1）以5 m的深度间隔划分监测面，共划分90层；

2）每层监测面上选取8个变形特征点，进行圆心拟合，研究相对变形情况；

3）井筒深度较深，以两层监测面特征点作为公共监测点，进行1次基准传递。

为检验激光基准传递的正确性，将测边交会法与提出的多距离交会法、平面参数转换法应用于新基准下激光点的坐标求解，并以计算得到的激光点坐标反算特征点坐标，对比旧基准坐标，分析精度情况，坐标偏差如图5所示，坐标计算结果比较如表1所示。

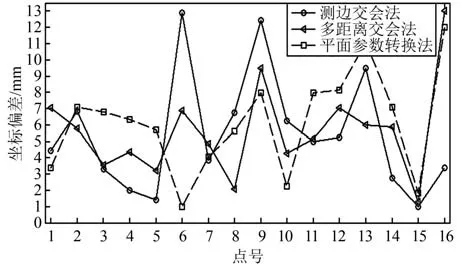
图5 3种方法的坐标偏差Fig.5 Coordinates Deviation of the Three Methods

表1 3种方法计算结果比较Tab.1 Comparison of Calculation Results of the Three Methods

结合图5和表1可得，3种方法计算公共特征点的坐标偏差最大不超过13 mm，整体在较小值范围内变化，具有较高的转换精度；3种方法计算的新激光点坐标，x方向互差最大为2 mm，y方向最大为1 mm，差异较小；在内符合精度方面，x、y方向中误差约为±2 mm，坐标中误差小于±3 mm，精度相当。总之，这3种方法计算结果差异较小，应用于新激光点坐标计算具有较高精度。

将各层监测面的拟合半径与设计半径相比较，计算拟合半径偏差如图6所示，并绘制井筒的三维立体图如图7所示，为直观地观察井筒变形情况，对井筒半径进行了放缩处理。

由图6、图7可得：

图6 各层拟合半径偏差Fig.6 Deviation of the Fitting Radius of Each Floor

图7 井筒三维立体图Fig.7 Three-Dimensional Diagram of the Shaft

1）井筒井口位置的变形程度小，接近设计半径，可以选择作为形变分析的基准。

2）井筒下部第88～90层，靠近马头门位置出现外凸变形，半径偏差最大达到38 mm，考虑由于马头门位置细部结构多，长期荷载作用对井壁影响大，于是发生了明显位移现象。

3）井筒整体半径偏差在-10～16 mm内，变形程度小，但第30～33层和第62～64层为含水层与岩土层交界处，受地质影响，出现严重内凹变形，半径偏差范围在-39～-25 mm，并根据实地勘察，此处渗水严重，多处存在井壁剥落现象。应在此处增设排水设施，对破坏严重位置进行加固整修。

4）分析井筒下部第74～90层，井筒出现一定的倾斜变形，通过空间直线拟合［8］，得出倾斜度为0.039°，倾斜方向为西南方向。为不影响罐笼升降，应及时进行罐道垂直度调整，防止发生罐笼触壁危险。

5 结束语

本文对基准建立与传递、新激光点坐标计算等关键技术进行重点研究，提出的多距离交会法和平面参数转换法，应用于新激光点的坐标求解，减少了计算量，同时保证了较高精度，内符合检验结果为2～3 mm，提高了基于激光基准变形监测方法的实用性。针对于我国大多数井筒的变形监测工作，基准传递都不超过两次，该方法可被广泛使用。