巧用逆向思维 解答数学难题

摘 要：在初中教育教学中，数学是一门既抽象、难度又大的科目，尤其是在解题环节，各种各样的难题层出不穷，对于师生双方来说均是一个严峻挑战.不少初中数学教师为帮助学生更好的解答数学难题，都在巧用逆向思维，指导他们创新解题思路，提高思维水平与解题能力.

关键词：逆向思维;数学难题

中图分类号：G632   文献标识码：A   文章编号：1008-0333（2022）08-0068-03

收稿日期：2021-12-15

作者简介：王康平（1977.12-），女，福建省福州人，本科，中学一级教师，从事初中数学教学研究.

逆向思维指的是对司空见惯、似乎已成定论事物或观点反过来思考的一种思维方式.初中数学教师可指导学生巧用逆向思维解答难题，使其敢于“反其道而思之”，思维向对立面的方向发展，让他们从问题的相反面深入探索，从而树立新思想、创立新形象.

1 巧妙利用逆向思维，解答二次函数难题

初中数学知识属于小学的后续、延伸与进阶，难度和深度也随之提升，学生在日常学习过程中，遇到的难题也更多，教师可引领学生巧妙运用逆向思维处理题目，使其别具匠心的解答数学难题，让学生慢慢消除畏难情绪.

例1 如果方程2x2-（4k+1）x+2k2-1=0，x2-2（k+1）x+k2-2=0，x2-（2k+1）x+（k-2）2=0中至少有一个方程存在实数根，求k的取值范围.

解析 由于“至少有一个方程有实数根”与“三个方程均无实数根”是相互对立的，那么先從这个问题的反面思考，即为从三个方程均无实数根的角度来考虑，也就是从△1、△2、△3三者均小于0中求出k的取值范围，再从实数中排除这个k的取值范围即可.

2 巧妙运用逆向思维，解答几何证明难题

证明题也是初中数学教学中比较常见的一种题目类型，对学生的逻辑思维能力、分析能力、空间意识与认知水平要求更高.教师可以指引学生巧妙运用逆向思维解决结论难以论证的数学难题，从结论着手展开分析与探讨，从而理清证明思路、确定证明流程，使其找到正确的证明方法，增强解题自信.

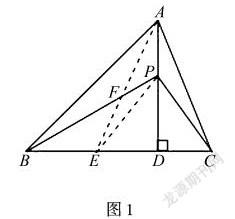
例2 如图1，在△ABC中，AB>AC，AD⊥BC于D，P为AD上任意一点，求证：PB-PC>AB-AC.

解析 本题是一道思维含量很高的题目.学生如果按照正向思维的思路分析题目，这道几何证明题很难从给出的已知条件确定证明思路与找到证明方法，假如运用逆向思维从要求证的结论出发，就能轻松的找到切入点，利用垂直平分线的性质，将线段AC、PC转移，再根据三角形三边关系定理证明即可.

3 巧妙应用逆向思维，解答一元一次方程难题

在以往的初中数学课程教学中，大部分学生分析和解决题目时，容易陷入到思维定势当中，正迁移方面有利于题目的求解，负迁移则不利于解题的正确性.所以，初中数学教师在解题教学中，可引导学生巧妙应用逆向思维，从结论往回推，使其摆脱思维定式的负迁移，最终顺利解答数学难题.

例3 小明的妈妈购买几桶牛奶，第一天，全家人喝掉全部牛奶的一半零半桶;第二天，又喝掉第一天剩下的一半零半桶;第三天，小明把家中仅剩下牛奶的一半零半桶喝完，这时妈妈所购买的牛奶刚好全部喝完，求妈妈一共购买了多少桶牛奶？

解析 本道题从正面较难求解，教师可指引学生应用逆向思维分析这一难题，设牛奶第二天喝完后还剩x桶，则x2-12=1，解得x=1，这表明牛奶第二天喝完后还剩余1桶，第二天没喝之前则为3桶，由此推理出第一天没喝之前的牛奶是7桶，也就是说妈妈一共购买了7桶牛奶.这样学生使用逆向思维解答了常规思维无法解决的问题，提升了学生的解题效率.

4 巧妙采用逆向思维，解答反比例函数难题

逆向思维和常规思维不同，是反过来思考问题，采用大部分人没有想到的思维方式去探讨问题，目的是希望“出奇制胜”，结果通常别有所获.具体到解答初中数学难题而言，教师可指导学生换个视角思考，将复杂问题变得简单化，以此锻炼他们解题思维的发展，使其解题速度和正确度得以提高.

例4 在平面直角坐标系中有三点A（2，4），B（3，5），P（a，a），将线段AB绕点P顺时针旋转90°得到CD，其中A，B对应点分别为C，D.若a=4，将函数y=4x（x>0）的图像绕点P顺时针旋转90°得到新图像，直线AB与新图像的交点为E，F，则EF的长为（直接写出结果）.

解析 本题主要考察反比例函数和一次函数的交点问题，可巧用逆向思维来解题：设直线AB的解析式是y=kx+b，把点A（2，4）与B（3，5）代入其中，得到直线AB的解析式为y=x+2，直线AB与新图像的交点在过A点与AB垂直的直线上，该直线的解析式是y=-x+6，所以反比例函数同y=-x+6的两交点距离就是EF的距离.

5 巧妙应用逆向思维，解答图像平移类难题

函数图象平移是初中数学的重要知识点，习题情境复杂多变.为更好的提高学生解答该类习题的能力，不仅要求学生能深入的理解函数图象平移的规律，搞清楚函数图象平移方向与相关参数之间的关系，而且要求学生掌握相关的解题技巧，尤其能够结合具体的习题情境采用逆向思维进行分析，迅速的找到正确答案.

例5 如图2，抛物线y=-12x2+7x-452与x轴交于A、B两点，将抛物线在x轴上方的部分记作C1，将C1向左平移得到C2， C2和x轴交于B、D两点，若直线y=-12x+m和C1、C2共有三个不同的交点，则m的取值范围为（  ）.

A.52C.52gzslib202204031116解析 令y=-12x2+7x-452=0，解得B（5，0），A（9，0），平移后C1、C2有共同的交点B.则可得D（1，0），C2对应的抛物线为y=-12（x-3）2+2，直线y=-12x+m和C1、C2共有三个不同的交点.若其刚好过点B时和C1、C2有两个交点，继续向上平移，会出现三个交点，将B（5，0）代入y=-12x+m，解得m=52，要想满足题意则m>52.采用逆向思维，从给出的选项出发排除BD两项.观察A、D两项，A项52

6 巧妙应用逆向思维，解答情境新颖的难题

初中数学测试中往往会出现一些情境较为新颖的习题，对学生理解能力要求较高.解答该类习题需要认真审题，吃透题意，根据题干创设的情境灵活应用逆向思维找到解题的突破口.

例6 已知如圖3所示的计算机程序，如果x为正整数，最后输出的结果为656，则开始输入的x值可能有（  ）.

A.2个  B.3个  C.4个  D.5个

图3解析 解答该题的关键在于能够读懂图中表示的运算规则.若知道了最后的输出结果，可采用逆向思维进行逆向运算求出x的值.根据题意可知如果只循环一次便输出结果可得5x+1=656，解得x=131;若循环两次输出结果则由5x+1=131，解得x=26;若循环三次输出结果则由5x+1=26，解得x=5;若循环四次输出结果则由5x+1=5，解得x=4/5，其不是正整数，因此，这种情况是不存在的.分析可知输入的X的值可能有131、26、5共3个，选择B项.

7 巧妙应用逆向思维，解答综合性难题

初中数学部分习题考查的知识点较多，综合性较强，需要积极联系所学采用逆向思维，判断相关参数之间的关系.

例7 若点P（x，y）的坐标满足x+y=2a-b-4x-y=b-4，且点P不在x轴上，若关于z的不等式yz+x+4>0的解集为z<23，求关于t的不等式at>b的解集.

解析 该题考查的知识点较多，主要有：二元一次方程组的解法、不等式、点的坐标等.根据题意不难求解出x=a-4，y=a-b，∵点P不在x轴上，∴a-b≠0.∵yz+x+4>0，∴（a-b）z+a>0，∵其解集为z<23，根据不等式知识可知，a-b<0，则a0，b>0，则由不等式at>b可得t>ba=52，∴不等式at>b的解集为t>52.

参考文献：

[1] 韩秀杰.初中数学教学中学生逆向思维能力的培养策略[J].学苑教育，2021（30）：59-60.

[2] 纪红芳.逆向思维在初中数学解题中的应用[J].数理化解题研究，2021（29）：46-47.

[3] 陈杰锋.浅谈初中生数学逆向思维能力的培养[J].数学学习与研究，2021（29）：51-52.

[4] 赵刚，马青.初中数学教学中学生思维品质培养探析[J].天津教育，2021（27）：32-33.

[5] 沈晓生.引导初中数学深度学习的逆向思维能力培养策略[J].中学数学，2021（16）：36-37+49.