多功能动态波束调控的太赫兹编码超表面

王禄炀，兰 峰,2*，宋天阳，何贵举，潘一博，张雅鑫,2，陈 智，杨梓强,2

(1.电子科技大学 电子科学与工程学院，四川 成都 611731；2.电子科技大学 长三角研究院(湖州)，浙江 湖州 313001；3.电子科技大学 通信抗干扰技术国家级重点实验室，四川 成都 611731)

0 引言

太赫兹通信与编码超表面技术被广泛认为是发展6G无线通信的两项关键候选技术。一方面，太赫兹通信具备大容量高速信息传输的能力[1-3]；另一方面，编码超表面有望以低成本和高度集成化的形式实现对信道环境的重构[4-5]。因此，发展太赫兹编码超表面技术对于在复杂信道环境中实现大容量高速通信具有重要意义。在微波至毫米波段，通常采用二极管作为数字开关元件进行动态编码调控[6-10]，而在太赫兹频段二极管复杂的内部结构产生了严重的寄生耦合，因此国内外研究者转而探索了基于液晶材料、二氧化钒薄膜、石墨烯等动态控制元件对太赫兹波进行动态波束重构[11-15]。然而，目前的太赫兹超表面器件仍然面临着低寄生集成、相位分布精度、调控速率等关键性问题，同时一些半导体元件还受到工艺制备水平和成本的限制。为克服上述阻碍，通过采用HEMT作为动态控制元件，设计了基于非对称谐振调控的1 bit相移编码单元。通过构建镜像子阵来实现阵列相位分布的准二维控制，结合多种阵列编码方案对太赫兹波进行多功能波束重构，进一步为发展太赫兹编码超表面在无线通信领域的实际应用奠定了研究基础。

1 相移单元和编码阵列设计

图1为本文提出的编码超表面相移单元和编码阵列的原理图。如图1(a)所示，单元结构包括表面嵌入AlGaN/GaN HEMT的复合金属图形、碳化硅介质衬底、金属反射底板。表面金属图形由两条长度不同的微带结构、一条横跨HEMT栅极的信号线、两条与微带结构相连的地线构成。HEMT嵌于两条微带结构之间的间隙处，形成与太赫兹波相互作用的非对称偶极子谐振结构。由于AlGaN/GaN异质结间的压电极化效应和自发极化效应，在异质结交界面会形成二维电子气(Two-Dimensional Electron Gas，2DEG)沟道，通过外加偏置电压可控制2DEG沟道的载流子浓度，从而调节单元结构对入射波的非对称谐振强度。通过在不同非对称谐振模式之间切换，使单元相位响应产生接近180°的相移变化。在此基础上根据相控阵理论和编码超表面原理，在360°相位周期内，1 bit编码将具有180°相差的两种单元状态，以二进制编码为0和1。通过将单元在二维平面上以周期尺寸p排列构成如图1(b)所示的1 bit编码超表面。沿+y方向上，每个单元之间共享相同的偏置馈线构成一个集体控制的单列模块，栅极馈线引至阵列边缘连接外置载板通过FPGA输入电压信号，地线则连接至阵列中央，通过横跨一条馈线使得每列控制模块共地。通过x轴为对称轴在-y方向设置镜像子阵，构建准二维控制的阵列。镜像子阵之间可实现相互独立的波束重构，相比传统一维列控的方式在提高了阵列对波束调控灵活性的同时，还不会产生多余馈线增强寄生干扰。

(b) 编码阵列图1 相移单元及编码阵列原理图Fig.1 Schematic diagrams of the phase-shift unit and coding array

通过在三维电磁仿真软件CST中通过设置Flout端口模拟周期边界条件，计算了在0.32～0.38 THz频段内，太赫兹波以x极化方向正入射下的单元幅相响应及谐振电场分布，通过仿真优化后的单元几何参数为：p=200 μm、h=200 μm、a=25 μm、b=55 μm、w=5 μm。德鲁德模型作为一种经典色散模型可用于模拟HEMT中沟道载流子浓度的变化情况[16-18]，其表征的等效复介电常数为：

(1)

式中，GaN的无穷高频相对介电常数ε∞=9.8。虚部中的碰撞频率νc与HEMT电子迁移率相关。ωp为等离子频率，与载流子浓度Ns的关系为：

(2)

涉及的参量包括电子电荷量e、真空介电常数ε0、沟道深度d和GaN电子有效质量m*。如图2所示，模拟了耗散型HEMT的载流子浓度从6×1012cm-2减小至0.75×1012cm-2过程中的单元幅相响应变化曲线。在起止两个浓度状态之间，0.345～0.362 THz频段的相移量超过了160°，带宽达到17 GHz。在0.35 THz频点附近，两个浓度状态之间的幅值均接近-7.5 dB，且达到了178°的最大相移量。因此，可将载流子浓度为6×1012cm-2和0.75×1012cm-2两个状态的单元分别以二进制编码0和1表示。

(a) 单元幅值

(b) 单元相位图2 不同载流子浓度下的单元幅相响应Fig.2 Amplitude-phase responses of the unit with different carrier concentration

两个编码状态之间的单元相移主要是依靠载流子浓度变化来调节非对称谐振强度实现的，通过模拟两种状态下的单元谐振电场分布，直观地解释了这种非对称谐振机制。如图3所示，长微带结构相比短微带结构聚集了更强的电场，从而形成非对称谐振。在编码0状态切换至编码1状态的过程中，增强了微带结构上的非对称谐振强度。不同于传统基于长短偶极谐振切换或是LC-偶极谐振切换的方式，这种基于非对称谐振调节实现单元相移调控的方式克服了HEMT在太赫兹频段的容性寄生，在低开关比下即可实现宽带的大范围相移调控。

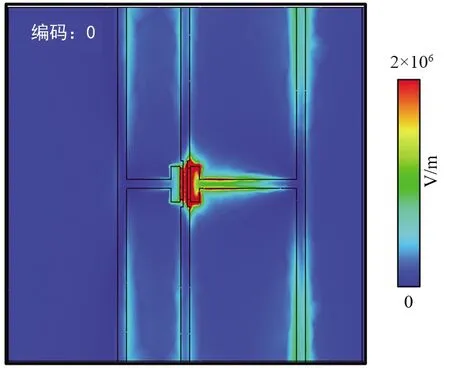
(a) 编码0单元

2 多功能编码波束调控

为基于编码超表面对太赫兹波进行多功能波束调控，通过采用分数化编码[19]、卷积编码[20]、分块编码和GRS(Golay-Rudin-Shapiro)编码[21]四种编码方案，分别实现连续性波束扫描、多波束调控和RCS缩减。所采用的编码方案计算出的编码矩阵对应着编码超表面阵列上的相位分布，呈现出了从信息域到物理域的数字化映射关系。为获得更丰富的编码资源，在图1(b)所示的阵列结构基础上，阵列扩大至由64×64个单元构成，其中每1×32个单元构成一个集体控制的单列模块，两个互为镜像的子阵各自含有64列控制模块。通过对大规模阵列进行编码数值计算，实现了太赫兹波的多功能波束重构设计。

2.1 连续性波束扫描

为在编码超表面上实现波束的连续性扫描和精准的定向反射，在之前的工作当中提出了一种分数化编码方案[19]。根据广义斯奈尔定律，假设阵列上的相位按dφ梯度分布，同相位周期由单元边长为p的N个单元排列而成，反射波束的角度为：

(3)

当dφ=180°时对应1 bit编码的情况，N=1、N=2和N=3对应的周期编码序列分别为[…0 1 0 1…]、[…0 0 1 1…]和[…0 0 0 1 1 1…]，同理可对N取任意正整数的情况进行编码。由于N只能取正整数，这直接影响了反射角θ变化的连续性和精确度。基于分数化编码方案，通过近似编码排列对N取任意非零自然数时的情况进行等效。由于N的取值和周期编码序列之间具有一一对应关系，下文为简化描述将用N来表示阵列的实际编码情况。

在频率为0.35 THz的平面波正入射下，图4为针对所述尺寸为p=200 μm的编码相移单元，计算了以步长ΔN=0.01从N=3到N=12进行1 bit编码后，在±60°视场范围内的波束方向图，分数化编码使反射波束有效填充了N取整数时留下的角度盲区，实现了在-45°～-10°和10°～45°范围内的双波束连续扫描。

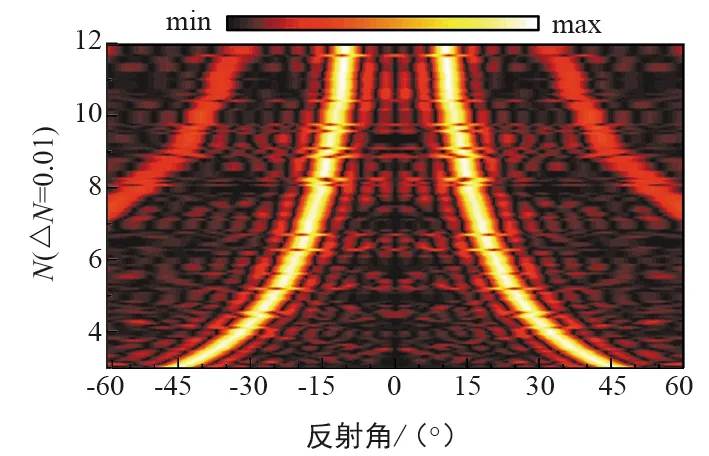
图4 双波束连续性波束扫描Fig.4 Dual-beams continuous beam scanning

2.2 多波束调控

以0.35 THz平面波正入射时，图5分别为编码超表面利用分块编码和卷积编码进行多波束调控的远场方向图。受益于特殊的准二维馈线排列方式，图5(a)将编码超表面划分为两个区域，以N=6排布编码矩阵C1控制±21°上反射的双波束，以N=32排布编码矩阵C2控制±3°上反射的另外一对双波束，从而使整个阵列达到控制四波束反射的目的。

根据卷积编码理论，对于任意两个分别控制波束在θ1和θ2方向反射的编码矩阵C1和C2，作卷积操作后将获得一组新的编码矩阵Ccon，控制波束在θ=sin-1(sinθ1+sinθ2)方向上反射。由此可见，通过两组编码波束的卷积操作，可将其中一组编码矩阵的波束在另一个波束方向上合成，因此本文考虑对两组双波束采用卷积编码实现四波束调控。如图5(b)所示，将N=6排布的编码矩阵C1和N=32排布的编码矩阵C2进行卷积操作后，新的编码矩阵Ccon可由C1和C2在360°相位周期内进行二进制加法运算后获得，并在-21°±3°和21°±3°方向上实现四波束重构。

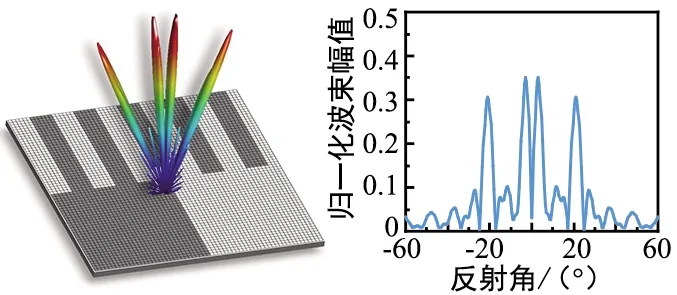
(a) 基于分块编码

(b) 基于卷积编码图5 多波束调控的远场方向图Fig.5 Far-field patterns of multi-beams manipulation

2.3 RCS缩减

要实现编码超表面的RCS缩减，需要排列编码矩阵将入射波向各个方向尽可能均匀地进行散射。利用GRS多项式是一种具有固定编码排列的次优化算法。GRS多项式由具有纠缠递推关系的P型和Q型两种类型组成，多项式系数构成了含有两种元素{-1,1}的GRS序列，对应着两个状态的1 bit编码单元。序列长度L需满足2的指数倍关系，以保证GRS序列能够严格关联到多项式，从而展现出有利于增强散射的光谱平坦性。GRS序列{Cn}可通过固定的递推算法获得，令S0=1，S2n=Sn，S2n+1=(-1)n，其中n=0,1,…,L-1。对于P型序列，满足Cn=Sn;对于Q型序列，当n=0,1，…,L/2-1时满足Cn=Sn，当n=L/2,L/2+1,…,L-1时满足Cn=-Sn。

随着序列长度L的指数倍增加，GRS编码会体现出更完美的光谱平坦性，从而增强散射能力。因此根据序列长度L=64的两种GRS编码，图6为增强散射后的远场方向图。由于P型和Q型两种编码具有纠缠递推关系，因此在相同的序列长度下都展现出了相当的增强散射能力，在±60°范围内的反射效率均低于20%。

(a) P型GRS编码

3 结束语

本文设计了一种基于HEMT动态调控的编码单元，通过调节HEMT沟道中载流子浓度，调节单元结构非对称谐振的强度，在低开关比下实现了带宽高达17 GHz的大相移调控，并在0.35 THz附近达到最佳工作频点，最大相移达到了178°。在此基础上构建的1 bit编码超表面阵列利用分数化编码，在±10°～±45°范围内实现了双波束连续性扫描。此外,还同时利用分块编码和卷积编码实现了四波束调控，以及基于GRS编码增强散射实现了RCS缩减。所设计的1 bit编码超表面提供了一种点对点和多通道复用的通信技术方案，此外还有望应用于超分辨雷达成像或是被动目标检测领域，并构建基于编码超表面辅助的通感一体化方案。