金刚石刀轮滚压脆断单晶硅和蓝宝石的实验研究

陈 绒，周 聪，谢 晋*，陈钊杰

（1.广东科技学院，广东 东莞523083；2.华南理工大学 机械与汽车工程学院，广东 广州510641）

1 引 言

单晶硅和蓝宝石作为半导体衬底材料，具有优越的性能［1-2］，已被广泛应用于LED、CMOS、MEMS器件制造产业［3-5］。在制作此类微电子器件时，需要对基底材料上光刻后的芯片电路进行分割并封装，切割质量直接影响着器件质量和成本［6］。此外，硬脆性硅和蓝宝石易产生裂纹，加工难度大［7-8］。

玻璃基板常采用硬质合金刀轮滚压切割［9］，但其寿命和精度较低；芯片切割采用金刚石高速旋切［10］，但由于磨粒产生应力集中，易出现崩边［11］。激光切割会残留熔融物质和微观裂纹［12］。也有学者提出一种干净平滑的冰辅助激光切割，但增加了成本［13］。1921年，A.A.Griffith提出了微裂纹理论，Griffith认为，实际材料中存在许多细小的裂纹或缺陷。在外力作用下，这些裂纹和缺陷附近产生应力集中现象。当应力达到一定程度时，裂纹开始扩展导致断裂。所以，断裂不是两部分晶体沿整个晶面拉断，而是裂纹扩展的结果［14］。

以此理论为基础，早期采用单点金刚石刀具划线切断单晶硅，但是对刀刃精度要求较高［15］。因此，在采用直径50 mm左右的金刚石砂轮片高速旋转划线切割时，需要在位修整砂轮片尖端［16-17］。由于半径大的砂轮片切割时有不规则微裂纹横向扩展乃至边缘破碎，直径2 mm左右的金刚石刀轮已逐渐开始被产业化应用［18-19］。此外，刀轮滚压压力和深度与表面质量的关系也一直被探究［20］。

在本研究中，利用金刚石微刀轮对单晶硅及蓝宝石进行滚压脆断分割。根据脆性材料特性，微裂纹扩展机理，研究刀轮角度和滚压压力对工件材料应力分布的影响。此外，实验研究不同工艺参数对裂纹扩展和断面质量的影响。最终应用于集成电路芯片的切割工艺中。

2 精密滚压应力场分析

2.1 刀轮精密滚压脆断模型

图1为刀轮精密滚压脆断过程图。在施加滚压压力p的作用下，使用刃端角度为α的金刚石刀轮在单晶硅和蓝宝石表面进行滚压，划痕下方产生垂直裂纹。然后，通过施加力矩，垂直裂纹沿脆断面扩展，产生脆断分离［21］。采用ANSYS仿真软件分析单晶硅和蓝宝石滚压脆断过程的应力分布。在仿真条件中，将刀轮定义为刚体，刃端角度α为115°和120°，尖端半径r为0，将工件材料定义为弹性体。单晶硅和蓝宝石的物理性质如表1所示。

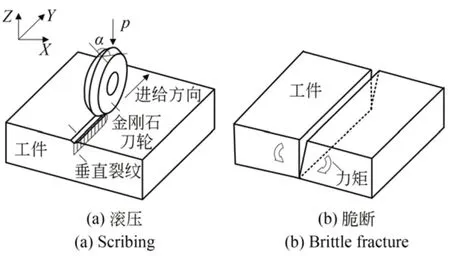
图1 刀轮精密滚压脆断过程Fig.1 Cutting wheel precision scribing and brittle fracture

表1 单晶硅和蓝宝石物理性质Tab.1 Physical properties of single crystal silicon and sapphire

2.2 刀轮角度对工件表面应力的影响

图2为滚压过程的刀轮刃端处应力分布云图。可以发现，工件表面应力的分布与刃端位置和刀轮形状有关，在刃端处，张应力达到最大，导致脆性材料的裂纹扩展。随着离开刃端距离增大，张应力逐渐减小，然后转变成压应力。沿着滚压方向，张应力范围逐渐扩大，最终工件表面形成直线划痕，用于最后的脆断切割。但是，刀轮刃端垂直下方的张应力因逐渐转变成压应力，裂纹不会进一步扩展。

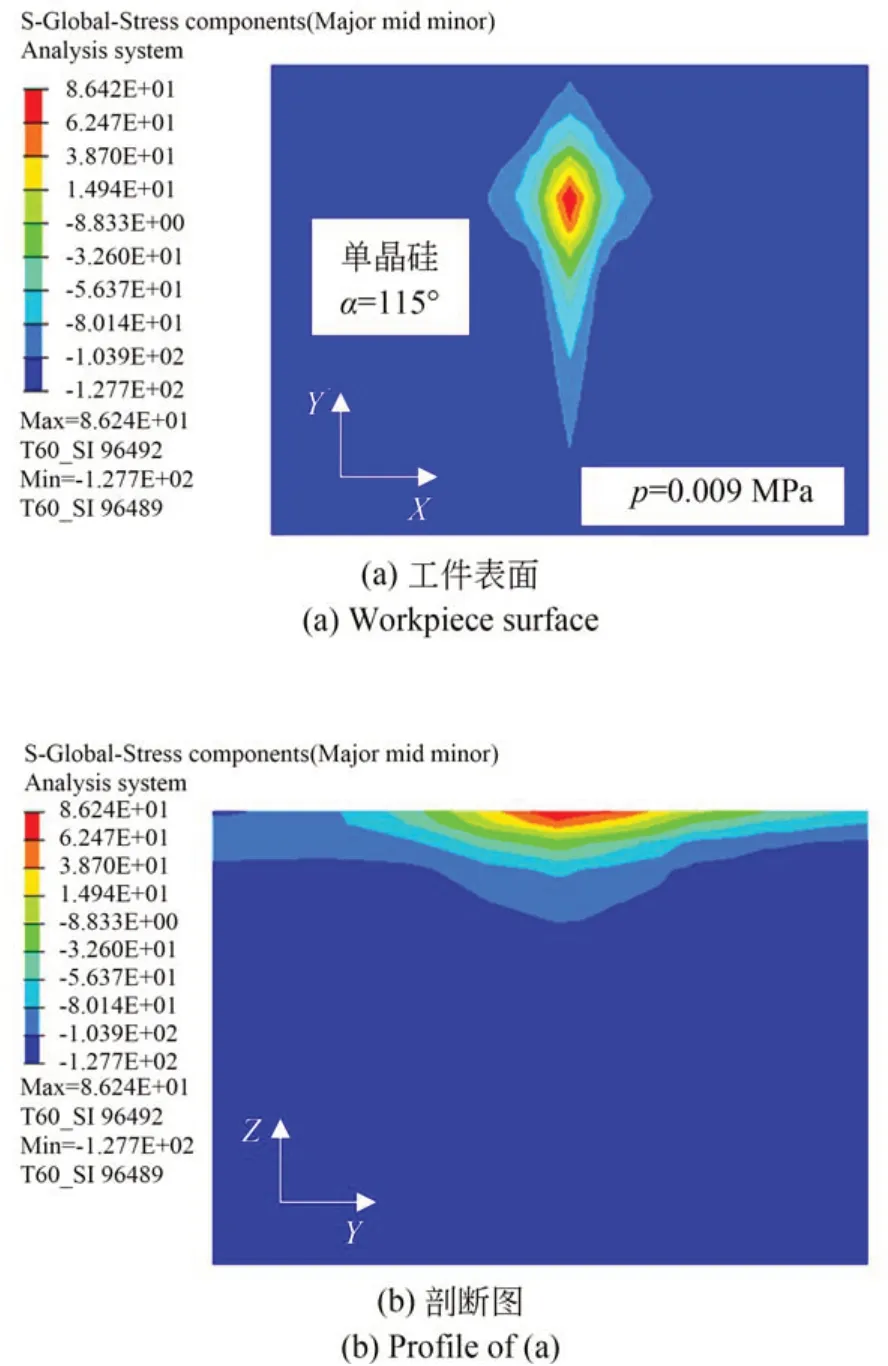
图2 滚压过程的刀轮刃端处应力分布云图Fig.2 Stress distribution at the edge of wheel during scribing

图3为刀轮角度α对最大表面应力σ的影响。可以看出，当α=115°，单晶硅的最大张应力为86.24 MPa，相 比α=120°的 应 力，提 高 了 约33.2%。相反，滚压蓝宝石时，α=115°的刀轮产生的最大张应力相比α=120°的低约5.2%。由此可知，刀轮滚压脆断韧度小且硬度较低的晶圆材料时，使用较大角度的刀轮会产生较低应力，可保证脆断面质量。

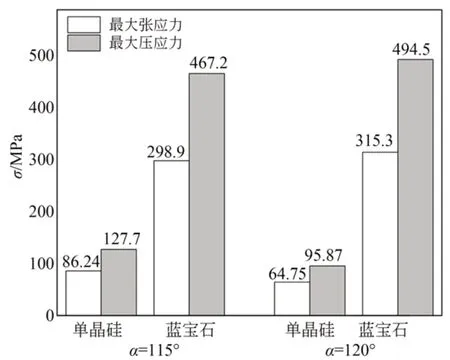
图3 刀轮角度α对工件表面最大应力σ的影响Fig.3 Effect of cutting wheel angleαon workpiece surface maximum stressσ

2.3 滚压压力对单晶硅和蓝宝石表面应力的影响

图4为滚压压力p与工件表面最大应力σ的关系。可以发现，随着滚压压力p的上升，工件表面应力σ线性上升。当滚压压力p较低时，单晶硅表面应力σ迅速上升，说明提高滚压压力p易产生更多裂纹，导致破碎。但是，蓝宝石表面应力σ上升速率比单晶硅低，原因是蓝宝石断裂韧度大，抵抗破碎能力更好，且精密滚压脆断所需滚压压力p也更大。此外，断裂韧度为1.9～5.5的材料适合的滚压压力p的范围约为0.03～0.07 MPa。

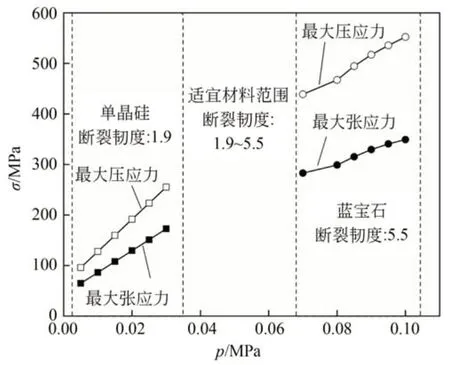
图4 滚压压力p与工件表面最大应力σ的关系Fig.4 Relationship between rolling pressure p and the maximum surface stressσ

3 滚压脆断实验数据及分析

3.1 工艺条件及参数

图5为刀轮滚压实验装置以及金刚石刀轮形貌。根据第2节的模拟仿真结果，选择合适工艺参数，进行滚压脆断实验。其中，工件材料通过真空吸盘固定，在刀架上装有金刚石刀轮，刀轮中央为刀轮轴安装孔，刀轮装入轮轴后固定在刀头部位，如图5（a）、（b）所示。图5（c）、（d）为实验使用的金刚石微刀轮形貌图，刃端半径r为5μm，用来保证精密滚压时的精度。金刚石刀轮规格如表2所示。

图5 实验装置及金刚石刀轮形貌Fig.5 Experimental setup and diamond wheel morphology

表2 金刚石刀轮规格Tab.2 Specifications of diamond cutter wheel

3.2 刀轮角度对滚压脆断断面的影响

图6为刀轮角度α对晶片断面质量的影响。可以看到，α=120°的单晶硅脆断面裂纹比α=115°的裂纹分布更加均匀，断面质量更高，但是，a=115°的蓝宝石脆断面相对α=120°的质量更高。结合第2节刀轮角度α对工件表面应力σ的分析，加工断裂韧度小和硬度低的材料使用α=120°的刀轮可以产生更低的应力σ，而加工断裂韧度大和硬度高的材料时使用α=115°的刀轮产生的应力σ更低。

图6 刀轮角度α对晶片断面质量的影响Fig.6 Effect of wheel angleαon wafer cross-section quality

由此可知，断裂韧度小且硬度低的材料应选择角度偏大的刀轮，滚压产生的应力更低，裂纹扩展更加集中，使芯片材料的断面品质更高。

3.3 滚压压力与断面质量的关系

3.3.1 单晶硅和蓝宝石的裂纹扩展

图7为滚压后的工件裂纹SEM形貌。可以看出，当滚压压力p较低时，单晶硅产生明显微裂纹，且随着压力上升横向裂纹逐渐增多，甚至产生破裂。对于蓝宝石，在p=0.07 MPa的滚压压力下，几乎没有微裂纹，提高压力p后开始出现垂直裂纹。结合应力分析结果，说明蓝宝石材料产生微裂纹所需要的应力约为单晶硅的5倍，且由于其断裂韧度大，硬度高，抵抗破碎和裂纹扩展的能力较强，需要更高的滚压压力p来产生垂直裂纹。

图7 滚压后的工件裂纹SEM形貌Fig.7 SEM morphology of crack in the workpiece after rolling

3.3.2 断面质量对比

图8为单晶硅划痕的SEM形貌图（α=120°）。使用不同压力p进行滚压脆断，获得脆断面。可以看出单晶硅在滚压处两侧出现边沿破碎，长度在1.12～1.35μm，且在增大滚压压力p的条件下，虽然滚压深度增加，但应力σ也增大，边沿破碎程度更大。

图8 单晶硅划痕的SEM形貌图（α=120°）Fig.8 SEM morphology of scratched silicon（α=120°）

图9为单晶硅划痕的断面光学形貌图（α=120°）。由图可知，在p=0.015 MPa时，划痕深度裂纹扩展相对均匀；在p=0.010 MPa时，断面发生鸡毛颈区，为非正常局部区域；p=0.020 MPa时断面发生非正常分离局部镜面区域。由此可知，单晶硅在滚压压力p为0.015 MPa左右时断面质量最优。

图9 单晶硅划痕的断面形貌图（α=120°）Fig.9 Cross-section morphology of scratched silicon（α=120°）

图10为蓝宝石划痕的SEM形貌图（α=115°）。可以看出，表面边沿破碎程度比单晶硅低约20%，且形状规则。这也说明，蓝宝石断裂韧度大且硬度高，能产生质量较好的划痕。对应的蓝宝石划痕的断面形貌如图11所示。从图中可以看到，在p=0.095 MPa时，蓝宝石断面划痕深度裂纹扩展较均匀，断面质量较高。

图10 蓝宝石划痕的SEM形貌图（α=115°）Fig.10 SEM morphology of sapphire scratches（α=115°）

图11 蓝宝石划痕的断面形貌图（α=115°）Fig.11 Cross-section of sapphire scratches（α=115°）

图12为滚压压力p与工件表面滚压深度h的关系。可以看出，滚压深度h与滚压压力p呈线性关系。单晶硅的滚压深度h在38～58μm，蓝宝石的滚压深度h在77～115μm，约为单晶硅的2倍。也可以预测，断裂韧度为1.9～5.5的材料适合的压力范围为0.03～0.07 MPa。对于不同角度刀轮的滚压效果，在单晶硅上使用α=120°的刀轮可以产生更深的滚压深度，断面质量较好，而在蓝宝石上使用α=115°刀轮的效果更优，这是由于滚压时产生的表面应力σ更小所导致的。

图12 滚压压力p与工件表面滚压深度h的关系Fig.12 Relationship between rolling pressure p and depth h of workpiece surface

综上所述，在进行晶片滚压脆断分离时，对应不同的晶片材料首先需要选择合适角度的刀轮，并在合适的滚压压力p下进行。过小的滚压压力p导致过小的应力σ，无法在划痕下方产生垂直裂纹；而过大的滚压压力p导致过大的应力σ，会产生破碎以及崩裂。其中，单晶硅滚压压力p为0.015 MPa，蓝宝石的滚压压力p为0.095 MPa时，滚压脆断后的断面裂纹扩展相对均匀，断面质量最优。

根据最优滚压压力p，结合图4的应力分析，单晶硅的最佳张应力σ在100 MPa左右，蓝宝石的为350 MPa左右，在适宜的外加应力σ下，切痕表面不会产生过多的边沿破碎，同时保证了一定的垂直裂纹长度（约10μm），可以获得高质量的断面。

3.4 集成电路芯片的滚压脆断切割

集成电路产业分为电路设计、芯片制造以及封装测试三个行业。在集成电路芯片封装过程中，首先需要对芯片进行切割，这一过程具有重要影响。在切割过程中，精密的切割轨迹能够保证在后续的分离过程中产生尽可能小的缺陷，不破坏表面电路，并减少后续的侧面磨抛时间。

以上述的刀轮精密滚压实验研究为基础，使用不同滚压压力p对集成电路芯片进行精密滚压脆断分离，观察刻有电路的芯片表面破碎情况，如图13所示。可以看出，在滚压压力p增大时，芯片的边沿破碎较为严重，出现缺口以及崩碎，影响芯片的性能。在选择滚压压力p较小的条件下产生的边沿破碎不会破坏晶片表面电路，保证性能。

图13 集成电路芯片分割后边缘形貌对比图Fig.13 Edge comparison after integrated circuit chips splitting

根据以上分析，使用带锯齿的120°金刚石刀轮以p=0.005 MPa的滚压压力对芯片背面进行滚压脆断分离，最终得到的芯片表面如图14所示。带锯齿的刀轮滚压脆断后，所得到的芯片边缘几乎不产生破碎，不会损伤芯片中的电路线。

图14 低损伤芯片分割形貌图Fig.14 Low damage chip splitting

4 结 论

（1）在金刚石刀轮精密滚压过程中，工件表面应力分布与与刃端位置和刀轮形状相近，张应力最大的部分集中在刀轮刃端下方，且工件表面的应力值与滚压压力总体呈线性关系。张应力过低，划痕下方无法产生垂直裂纹；张应力过高，会产生横向裂纹，易使芯片脆断边缘破碎和崩裂。

（2）在单晶硅精密滚压时，刀轮角度为115°产生的张应力相比120°约高33.2%，而在蓝宝石中，刀轮角度为115°产生的张应力相比120°刀轮约低5.2%。在选择刀轮角度时，硬度和断裂韧度越大的材料选用角度偏小的刀轮，滚压时产生的应力更低，裂纹扩展范围更加集中，工件材料的断面品质更高。

（3）在进行对单晶硅与蓝宝石精密滚压脆断时，滚压深度与滚压压力成正相关关系。同时，在合适的滚压压力和张应力范围内，划痕表面边沿破碎低至约1μm，微裂纹扩散均匀且方向一致，断面质量高。其中，单晶硅滚压压力为0.015 MPa，张应力在100 MPa左右，蓝宝石的滚压压力为0.095 MPa，张应力在350 MPa左右时，滚压脆断后的断面裂纹扩展相对均匀，断面质量最优。

（4）将金刚石刀轮滚压脆断技术应用于集成电路芯片切割中可减少后续加工磨抛的时间，提高效率。滚压压力增大会引起芯片边沿破碎的增多，甚至出现缺口以及崩碎，影响芯片的性能。所以，在进行芯片切割时，应尽可能选择较小的滚压压力，选用带微锯齿的刀轮，保证芯片分离时表面电路完整性。