求解二次损失函数优化问题的分布式共轭梯度算法
2022-03-31于洁孟文辉
于洁,孟文辉
(西北大学数学学院,陕西 西安 710127)
1 引言
由于现代数据集的规模和复杂性激增,使用传统的集中式算法优化损失函数对集中服务器的性能要求非常高,甚至无法求解.而且目前许多大型工程规模的应用程序中,数据集是以分散的方式在集群上收集和存储的,典型的例子是用户点击量或搜索查询记录,因此开发利用分布式处理大型数据集的算法变得至关重要.
由于分布式优化的重要性,已有很多关于海量数据集分布式算法的文献问世.这些分布式算法分为两类,一类算法是基于损失函数的一阶导数信息,例如分布式梯度下降法[1-4],分布式对偶平均算法[5-6],分布式增广拉格朗日算法[7-8]和分布式交替方向乘子法[9-11]以及其各种变体.虽然它们之间有很大差异,但基本步骤都可以归结为先进行局部的梯度下降,然后与主机器交换变量和信息平均.由于这些算法仅利用了损失函数的一阶导数信息,导致对下降方向的曲率估计不准确,通常收敛速度较慢.另一类算法是基于损失函数的二阶导数信息来构造牛顿步长,但由于牛顿步长的分布式近似很难设计,基于真正二阶导数信息的分布式牛顿算法是不可行的.目前,基于损失函数二阶导数信息研究较多的是分布式牛顿类算法[12-15],此类算法比大多数一阶方法具有更快的收敛速度,但计算目标函数的二阶信息计算量较大.
本文的算法思想来源于共轭梯度法.共轭梯度法只需利用一阶导数的信息,克服了最速下降法收敛速度慢的缺陷,避免了牛顿法要计算Hesse矩阵并求逆的缺点,因此共轭梯度法是求解大型线性方程组最有效的方法之一[16].然而,目前在分布式环境中对共轭梯度算法的研究较少,为丰富这一方面的文献,本文在共轭梯度法的基础知识上设计一种分布式共轭梯度算法.特别地,共轭梯度法优化正定二次函数具有二次终止性,本文主要利用该算法对线性回归模型的二次损失函数进行优化.首先设计分布式共轭梯度算法的流程,其中子机器与主机器通过平均子机器上的信息互相通信,在每次迭代中进行两轮通信,且仅传输向量信息和标量信息,没有高阶信息的传输,通信成本较低.其次从理论上证明该算法是线性收敛的.最后通过模拟实验发现:分布式共轭梯度算法比ADMM[10]更快地趋于集中式算法,且其收敛速度随样本量的增加而变快,随机器台数的增加而减小;计算误差随样本量的增加而减小,随机器台数的增加而增大.
2 分布式共轭梯度算法
本节详细介绍对线性回归模型利用分布式共轭梯度算法优化其二次损失函数的具体流程.在每轮通信中,子机器与主机器相互交换消息,并且在两轮通信之间,子机器仅基于它们的本地信息进行计算,该本地信息包括本地数据集和之前接收的消息.
线性回归是一种简单且应用广泛的统计模型,本文针对其损失函数设计了一种分布式共轭梯度算法.由线性回归模型,生成N个样本数据{xi,yi}(i=1,2,···,N),

其中xi∈Rp,θ∈Rp,ϵi是均值为0,方差为1的独立高斯随机变量.
对回归问题(1),典型的损失函数是均方误差损失:
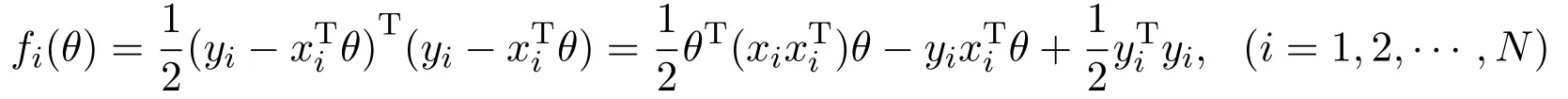
本文的目标是最小化局部损失函数之和(总损失函数):


然而,在大数据环境下,集中式服务器的可靠性差,且成本过高.在分布式算法中,将样本数据{xi,yi}(i=1,···,N)平均分给m台子机器 (假设N=nm),每台子机器有n组数据{xi,yi},则第j台子机器上的损失函数为

分布式算法的目标是最小化总损失函数:
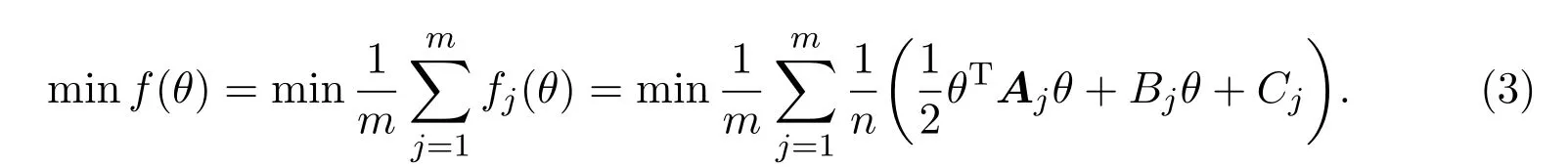
考虑无约束优化方法共轭梯度法,迭代格式如下θ(k+1)=θ(k)+λ(k)p(k),其中p(k)为共轭方向,λ(k)为步长因子,通过精确或者非精确线性搜索得到.
下面基于上述算法过程设计分布式共轭梯度法求解(3)式,最大的不同之处在于步长因子λ(k)的分布式近似.在第k次迭代中(k=0,1,···),每台子机器上的共轭方向法迭代公式为,其中p(k)为共轭方向,为步长因子.对于正定二次函数(2)式,精确线性搜索因子
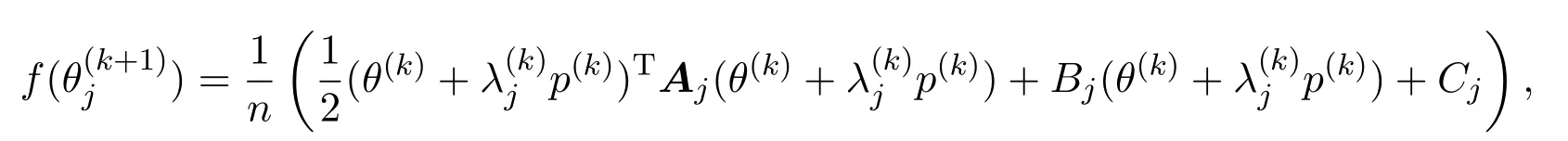
对上式求极小值点得到
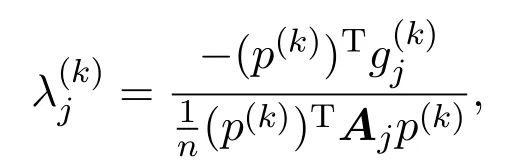


并分配给每台子机器,这就构成了第一轮通信.由主机器上的信息更新迭代点θ(k):
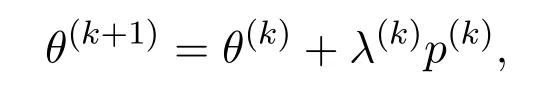
其中p(k)为当前迭代的下降方向.
利用当前迭代的全局梯度g(k),更新每台子机器的梯度:将获得的局部梯度传送到主机器上,计算全局梯度:

并更新主机器上的下降方向:p(k+1)=−g(k+1)+β(k)p(k),其中β(k)是F-R公式:
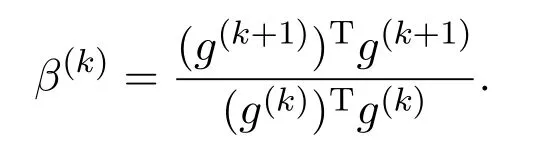
再将g(k+1),p(k+1)传播回每台子机器,这就构成了第k次迭代中的第二轮通信,具体通信方法如上图1所示.如此往复循环迭代,直至求出符合终止条件的最优解.

图1 第k次迭代过程中机器之间的通信示意图

1分布式共轭梯度算法Input:{xi,yi}(i=1,···,N),xi∈ Rp,yi是常数.规定:Aj=n∑i=1 xixTi 是p阶对称正定矩阵,Bj=n∑i=1-yixTi ∈ Rp是行向量,j=1,2,···,m,N=nm.Output:θ(k):每次迭代的最优解.1:initial θ(0):将第一台子机器最小化(2)式的解作为初始迭代点,发送给主机器,再传送回每台子机器;g(0)j =1 n(Ajθ(0)+Bj):计算每台子机器上的初始梯度,发送给主机器;g(0)=1 m m∑j=1 g(0)j,p(0)=-g(0):主机器上计算全局初始梯度和初始下降方向,由主机器将g(0),p(0)传播回每台子机器.2:for k=0,1,···,do 3: if|g(k)|>ϵ then 4: for j=1,2,···,m do 5: 计算每台子机器上的步长:λ(k)j = (g(k))Tg(k)1 n(p(k))TAjp(k).6: end for 7: 将 λ(k)j 传送给主机器,计算全局步长:λ(k)=1 m m∑j=1 λ(k)j,并分配给每台子机器.8: 在主机器上更新迭代点:θ(k+1)=θ(k)+λ(k)p(k).9: 更新每台子机器的梯度:10: for j=1,2,···,m do 11: g(k+1)j =g(k)+1 nλ(k)Ajp(k).12: end for 13: 将更新好的梯度传送给主机器,计算全局梯度:g(k+1)=1 m m∑j=1 g(k+1)j.14: 在主机器上计算:p(k+1)=-g(k+1)+β(k)p(k), β(k)=(g(k+1))Tg(k+1)(g(k))Tg(k).15: 并将g(k+1),p(k+1)传播回每台子机器.16: else 17: break 18: end if 19:end for
上述是分布式共轭梯度算法最小化二次损失函数的全部流程,如算法1所示,该算法仅利用了损失函数的一阶导数信息,在每次迭代过程中机器之间执行两轮通信,子机器将本地步长和本地梯度传输给主机器,主机器平均化之后再发送到每台子机器.该算法同时有计算简单和通信成本较低的优点.下节将给出算法的收敛性证明.
3 收敛性分析
本节主要分析分布式共轭梯度算法在二次损失函数上的收敛性.理论上证明了对二次损失函数(3)式,在满足子机器上的对称正定矩阵相似时,即
Aj≈Ak,j=k=1,2,···,m,
分布式共轭梯度算法具有线性收敛性.
对极小化问题(3),集中式服务器下的总损失函数为



由于A是正定对称矩阵,从而AH=A,则上式中第二个不等式是由引理3.1得到.证毕.
经过以上的理论分析可以证明分布式共轭梯度算法具有线性收敛速度,且当β越小时,即每台子机器上的正定对称矩阵Aj,j=1,2,···,m越相似,收敛速度越快.
4 模拟实验
本节主要论述分布式共轭梯度算法的初步实验结果.验证了分布式共轭梯度算法的误差在一定的迭代次数后与集中式性能相匹配,且较之ADMM收敛速度更快.在与ADMM的对比实验中发现,分布式共轭梯度法的误差与收敛速度受机器中样本量大小和机器台数的影响,而ADMM的收敛速度对机器台数并不敏感.
考虑使用合成数据集求解简单的线性回归模型,其中所有参数都可以被显式控制.根据模型yi=
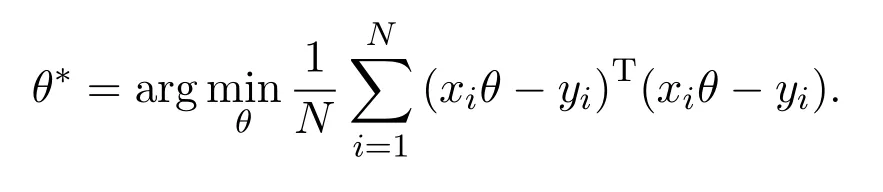
图2展示了在d=10,N=6000,m=20时,随着迭代次数的增加,均方误差逐渐减小,在迭代大约十次时收敛.为了对比,本文还实现了分布式ADMM[10],这是一种分布式优化的标准方法.并且观察到分布式共轭梯度算法比ADMM明显在更少的迭代次数中匹配于集中式性能.
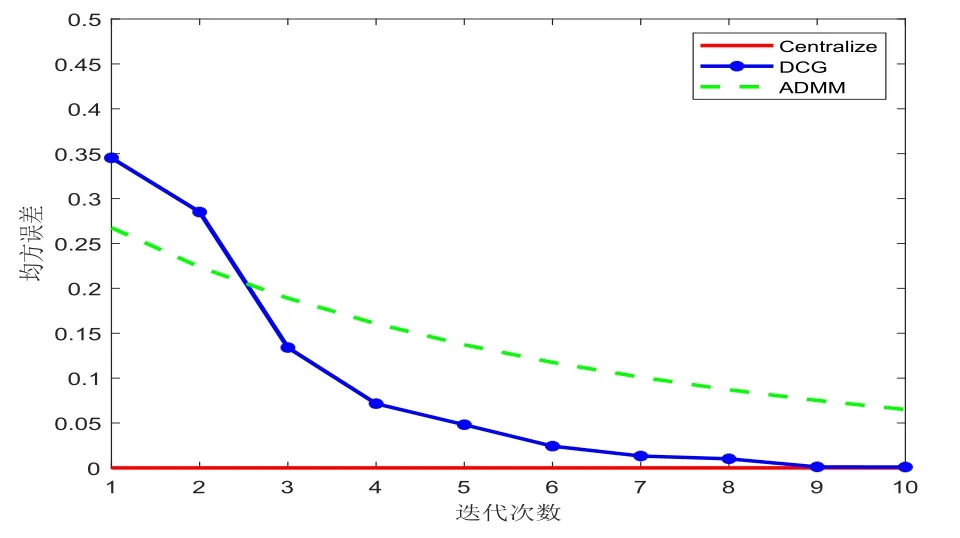
图2 DCG与ADMM对比图
图3显示了分布式共轭梯度算法和分布式ADMM在不同机器台数m下随样本总量N增加的收敛行为.分布式共轭梯度算法的结果清楚地表明了线性收敛性,而且收敛速度随着样本总量N的增加而提高,误差随N增加而减小.随机器台数m的增加收敛速度变慢,误差增大.(在m很大时,有可能导致不收敛,这可能由于每台子机器上样本量过少的缘故.)相比之下,虽然增加样本量N会提高ADMM的精度,但收敛速度较慢,并且收敛速度受机器台数m的影响较小.
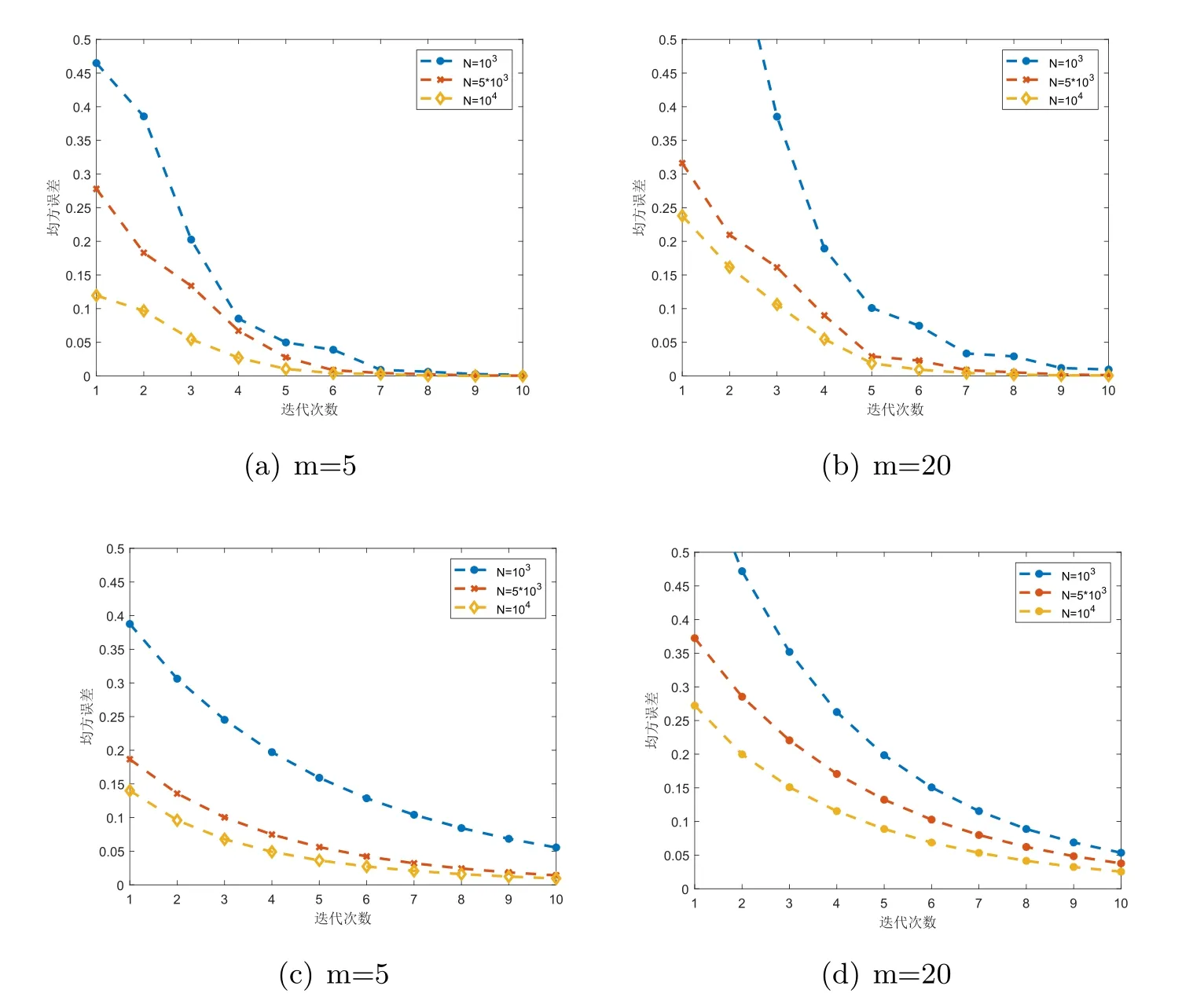
图3 DCG和ADMM收敛性能与样本量的关系图
5 结论
本文提出一种分布式共轭梯度算法,该算法具有计算简单和通信成本较低的优点.经过理论分析表明,所提出的算法在满足一定的条件下线性收敛.在合成数据集上,对线性回归模型进行模拟实验,并与研究成熟的分布式ADMM算法做对比,结果发现本文所提出的算法能在更少迭代次数下匹配于集中式性能,并且收敛速度明显快于ADMM.
由于个人电脑硬件设备的限制,文章中实验的数据量和维度都不足够大,但实验结果可以同理到大数据环境下.本文基于简单二次损失函数对分布式共轭梯度算法的性能做了研究,为未来将此算法扩展到非二次函数上奠定了一定的基础.
