核电机组二回路碳钢给水管道节流孔板下游流动加速腐蚀数值模拟研究

2022-03-31宗凌风周克毅黄军林司晓东徐青蓝

发电设备 2022年2期

宗凌风，周克毅，黄军林，司晓东，徐青蓝

(1. 东南大学能源热转换及其过程测控教育部重点实验室，南京 210096；2. 中国核动力研究设计院核反应堆系统设计技术重点实验室，成都 610213)

核电机组二回路的汽水输运管道大量使用碳钢，流动加速腐蚀(FAC)是影响管道安全性的重要因素之一[1]。FAC过程中，管道内壁保护性氧化膜被流动工质加速分解和破坏，无法有效抑制管壁基体的持续氧化[2]。管道持续减薄，并可能在机组运行过程中突然破裂，严重影响机组安全经济运行[3]。

FAC问题出现的早期，学者将其归因于单纯的机械冲刷。采取增加管径和减少弯角等措施后，FAC问题得到了缓解，之后一段时间内FAC问题未受到关注。1986年美国Surry核电站发生的管道破裂事故是FAC研究的转折点。事故中，给水泵下游弯管在机组运行时突然破裂，造成4死4伤的悲剧[4]。FAC致使局部管壁严重减薄是造成该起事故的主因。对FAC的研究自此受到高度重视，美国电力研究院(RPRI)、法国电力公司(EDF)、德国西门子公司(Siemens/KWU)等随即开展相关研究。然而，2004年和2007年，日本Mihama核电站和美国Iatan核电站又接连发生了严重的管道破裂事故，再次造成人员伤亡的悲剧[5]。分析显示，节流孔板及阀门下游的FAC是这些事故的主因。因此，迫切需要深入探究节流孔板下游的FAC机理，并提出有效抑制和预防节流孔板下游FAC的方法[6]。

在弯管、节流孔板和T形三通管等流场剧烈变化的奇点下游，最易发生FAC事故[7]。工质流经这些管道部件时，流向的剧烈变化及二次流不稳定性发展等因素，致使FAC速率显著增加[8]。CRAWFORD N M等[9]发现孔板和阀门的结构特性促使下游湍流靠近壁面，提高了壁面的传质速率。

开展FAC的试验研究需要搭建高温高压循环回路，并且对循环工质的pH、温度和溶氧[10]等有严格要求。随着计算流体动力学(CFD)的不断发展，其计算能力可以满足传质和腐蚀研究的要求，而精确的近壁网格和合理的近壁湍流模型可保证壁面传质数据的计算准确性。学者采用CFD方法模拟了节流孔板下游流场并分析了孔板形状对下游FAC的影响。YIN G等[11]结合k-ω剪应力输运湍流模型，模拟了孔板厚度和孔径比对孔板下游压力、流量和涡量分布的影响。AHMED W H等[12]采用模拟和试验验证，研究孔径比为0.25、0.50和0.75的孔板下游FAC，并用氢氧化钙制成试验段验证了数值结果。

国内外学者对直管、弯管等的FAC问题已开展了较为深入的研究，对管内流场影响FAC的机理有了一定的认识。相比之下，虽然对流场更为复杂的节流孔板下游FAC问题也有了一定的研究，但还未能形成完整的体系。部分学者针对孔板孔径比对FAC的影响展开了研究，但对节流孔板的倒角角度、厚度等几何结构因素影响近壁流场进而影响FAC的具体机制仍不明确，亦未在此基础上提出有效的缓解FAC的具体措施。笔者基于Sanchez-Caldera模型，采用数值模拟的方法，研究节流孔板下游FAC速率和位置的分布。在此基础上，重点分析了不同入口流速和倒角角度对节流孔板下游FAC分布的影响，以期为设计人员进行核电机组二回路给水管道节流孔板的设计选型提供参考。

1 FAC机理和模型

1.1 FAC机理

图1是FAC过程，即氧化膜形成和溶解的机理，其中δ为氧化膜的厚度，δy为传质边界层的厚度，δd为饱和层的厚度。FAC主要分为3个过程[13]：(1)金属基体表面失去电子生成Fe2+；(2)一部分Fe2+与水发生水合反应生成Fe3O4，另一部分Fe2+通过氧化膜的空隙传递到主体溶液中；(3)氧化膜进一步溶于水并扩散到主体溶液中。

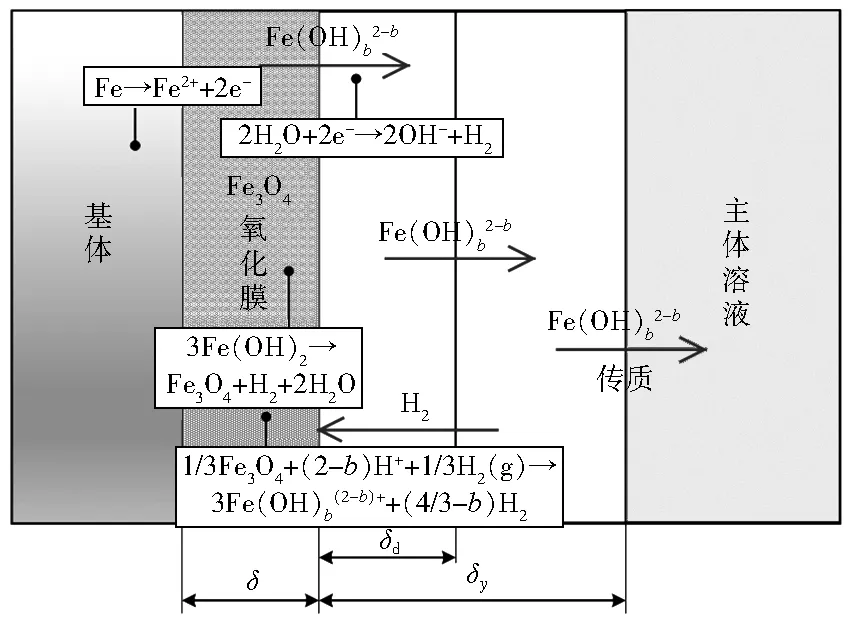
图1 氧化膜形成和溶解机理

第1个过程发生在基体/氧化膜界面处。在阳极，Fe失去电子生成Fe2+，发生氧化反应；在还原性溶液中，阴极处H2O得到电子，生成OH-和H2，发生还原反应。结合阳极和阴极的反应，第1个过程的电化学反应为：

(1)

此时，Fe2+和Fe(OH)2的浓度可以根据反应平衡常数获得。

第2个过程的反应是Fe(OH)2通过水合反应生成Fe3O4，即

(2)

该过程生成了底层致密、外层疏松的多孔氧化膜层[14]，剩余的可溶性含Fe组分通过氧化膜/主体溶液界面扩散到主体溶液中，并被不断流动的主体溶液带走，使得可溶性含Fe组分的溶解过程持续进行。

第3个过程，氧化膜在氧化膜/水界面处溶解，生成可溶性含Fe组分[15]。该反应过程由多个过程组合而成，可总结为以下化学方程式：

(3)

式中：b=0、1、2和3。

FAC过程由电化学腐蚀过程和传质过程共同控制。当主体溶液流速增加时，传质过程速度加快，体系内浓度差增大，基体Fe和氧化膜的活化和溶解反应速率加快，进而加快了FAC速率。

1.2 FAC预测模型

基于FAC机理，结合Sanchez-Caldera[16]模型，可获得FAC速率计算式为：

(4)

式中：KFAC为FAC速率，mm/a；Ceq为可溶性含Fe组分的溶解度，mol/L；C∞为主体溶液中可溶性含Fe组分的浓度，mol/L；K*为反应速率常数，m/s；k为传质系数，m/s；f为基体氧化膜界面Fe2+转化为氧化膜的比例；θ为氧化膜的孔隙率；DFe为可溶性含Fe组分在水中的扩散系数，m2/s。

BERGE P H等[17]认为，有一半的可溶性含Fe组分转化为氧化膜，因此f=0.5；主体溶液中，可溶性含Fe组分的浓度很低，因此C∞可忽略；活化反应速率常数远大于氧化层向主体溶液的传质系数，因此1/K*亦可忽略。式(4)可简化为：

(5)

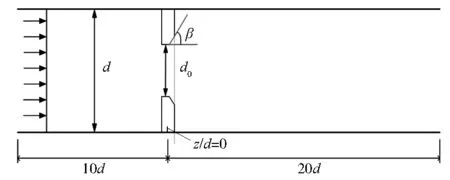
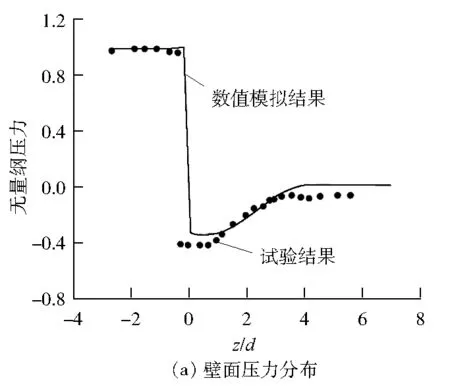
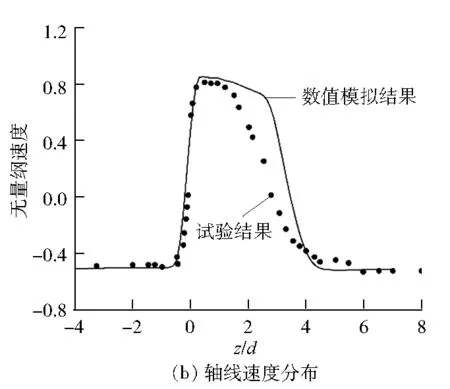
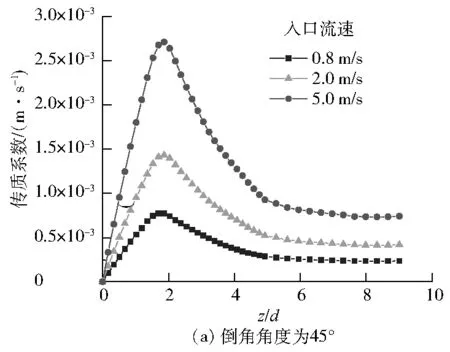
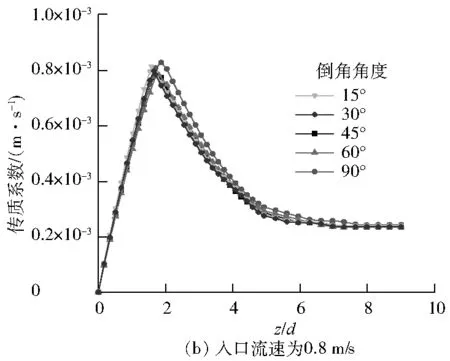
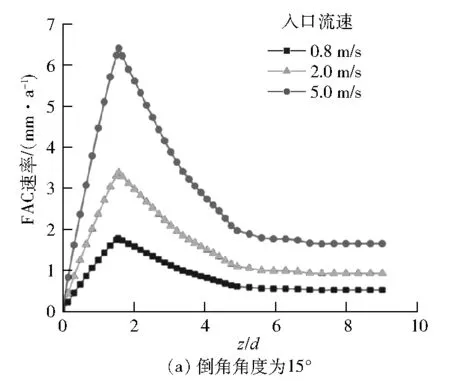
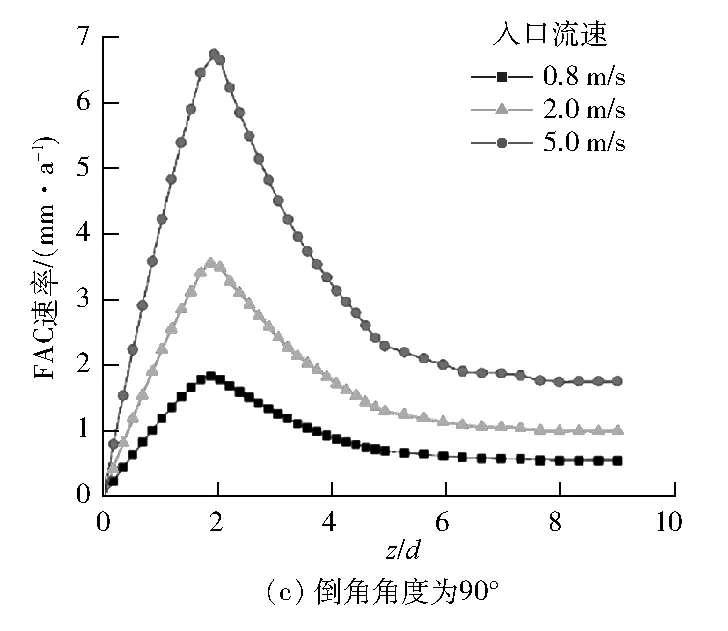
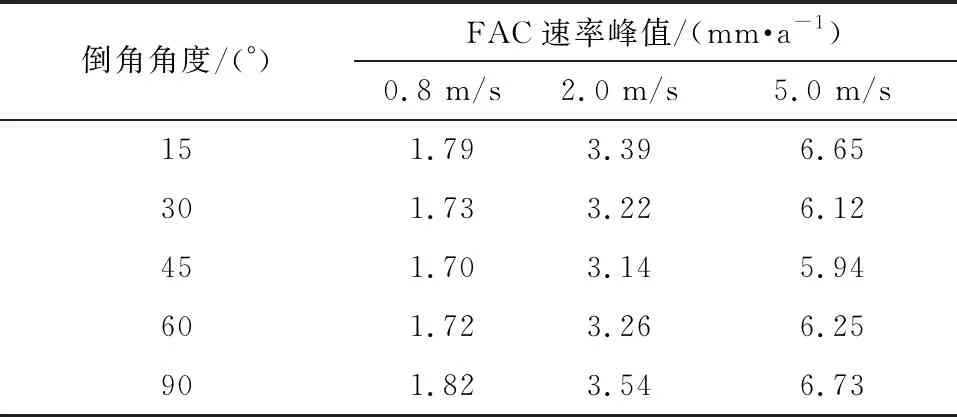
当流体温度T低于100 ℃时，δ约为5 nm；当T高于120 ℃时，δ约为1 μm。当T≤422 K时，θ=0.05%；当422 K

1.3 溶解度模型

高温低氧条件下，基体和溶液界面生成的Fe3O4氧化膜具有微溶性和渗透性，在主体溶液流过时会不断溶解。Fe在溶液中的溶解度可表示为Fe的可溶性组分的溶解度之和，即

Ceq=[Fe2+]+[Fe(OH)+]+[Fe(OH)2]+

(6)

式(3)可以分解为以下氧化物在氧化膜/主体溶液界面的溶解反应：

(7)

上述方程的反应平衡常数记为Kx(x=0、1、2、3)，则

(8)

因此，式(6)可简化为：

Ceq=(K010-2m+K110-m+K2+

K310m)[H2]1/3

(9)

式中：m为含Fe溶液的pH；[H2]为7.80×10-4～3.25×10-3mol/L[18]。

式(7)的化学平衡常数可表示为：

(10)

式中：R为理想气体常数，J/(mol·K)；A、B、C均为常数，其取值见表1[16]。

表1 参数A、B和C的取值

1.4 传质系数模型

由FAC机理可知，传质系数是表征FAC速率的重要参数之一。试验研究中，常用3个无因次准则数——雷诺数(Re)、舍伍德数(Sh)和施密特数(Sc)的组合形式来表示传质系数[19-20]：

(11)

式中：kFe为Fe的传质系数，m/s；d为特征长度，在管道内部，d的取值是管道的内径，m。

通过ANSYS软件求解连续性方程、动量方程和能量方程，计算孔板下游流速分布，基于流速和Re的关系式求出Re的分布，并代入式(11)即可得到孔板下游传质系数的分布。同时，计算采用如下假设：流动为定常不可压缩流动；忽略重力的影响；不考虑管子的散热。

2 计算结果与分析

2.1 溶解度

水化学条件选取核电机组二回路管道运行的温度压力范围，结合FAC高发的温度范围。具体取值如下：温度为150 ℃，压力为0.95 MPa，常温条件(25 ℃)下流体的pH为9.4，150 ℃条件下流体的pH为6.86，H2浓度为1.5×10-3mol/L。将上述取值代入式(9)，可以得到可溶性含Fe组分的饱和溶解度为6.95×10-8mol/L。

2.2 流场

孔板的几何模型见图2，管道内径d为50 mm，孔板直径d0为25 mm，孔板厚度为3 mm，孔板上游长度为10d，孔板下游长度为20d，即上游长度为500 mm，下游长度为1 000 mm，流体到达孔板时已经充分发展。将孔板出口平面作为坐标原点，则此处z/d=0(z为孔板下游到孔板的距离)，孔径比d0/d=0.5，孔板出水侧倒角角度β分别设置为15°、30°、45°、60°和90°。当倒角角度为90°时，孔板出水侧不存在倒角，即倒角角度为0°。

图2 孔板几何模型

在计算前处理软件ICEM中对几何模型进行网格划分，采取O形剖分的方法划分结构性网格，对孔板的倒角进行二次剖分，并对孔板倒角和孔板壁面进行局部网格加密处理。为保证计算精度，第一层网格的高度为0.3 mm，网格总数量为360万，网格质量分布在0.7～1.0，符合FLUENT软件求解器的计算要求。网格划分和孔板网格加密情况见图3。

图3 网格划分

在FLUENT软件求解器中，采用基于压力的求解方式，选用Realizablek-ε湍流模型，标准壁面函数，边界条件采用速度入口、压力出口。入口流速分别为0.8 m/s、2.0 m/s和5.0 m/s，管内压力为0.95 MPa。求解算法采用速度压力耦合的SIMPLE算法；动量方程、湍动能、湍动能耗散和能量方程采用二阶迎风离散格式，松弛因子采用默认值，收敛标准为1×10-4，对该模型进行数值计算。

将倒角角度为45°、入口流速为0.8 m/s的数值模拟结果和实验结果进行对比，结果见图4。由图4(a)可知：数值模拟结果较好地符合了壁面压力经过孔板时陡降的情况，与试验数据[12]符合较好。由图4(b)可知：数值模拟结果显示了流体在经过孔板时轴线速度陡增的现象，与试验结果一致。因此，可认为模拟的管内流场是准确的。

图4 孔板下游壁面压力和轴线速度分布

图5为倒角角度为45°时，入口流速为2.0 m/s时孔板下游横截面和管道中心截面的流场分布图。当流体流经孔板时，由于流道瞬间缩小，根据质量守恒定律，流体的流速增大；在通过倒角后，流道恢复到初始的横截面积。在孔板后流体发生分离的现象，在两侧孔板后形成对称的漩涡。由于两侧漩涡的存在，管道中心位置高速流体流通区域缩小，流出倒角后的流体中心速度继续增大；分离流体后和壁面重新附着，轴线速度也在达到最大值以后逐渐减小，最后趋于稳定。随着与中心处高速流体发生动量交换，管道外围流体的流速也逐渐增大，最后趋于稳定。

图5 入口流速为2.0 m/s时孔板下游横截面及管道中心截面流场分布图

由图5可知：管道下游流场呈中心对称分布，在z/d=0时管道外围流场分布不均匀，随后到z/d=0.8时趋于稳定。管内漩涡从中心位置向外围逐渐扩散，在z/d=4.0左右时，漩涡消失，流体重新附着。管道轴线处的高速流通区域面积先增大后减小，随着流体的流动，管道中心流体与外围流体发生动量交换，流速先增大后减小。

图6是入口流速为0.8 m/s时不同倒角角度孔板下游的流场分布图。

图6 不同倒角孔板下游流场分布

图6中截取了孔板下游-0.5d～5.5d流场变化比较剧烈的局部放大图。由图6可知：当倒角角度为15°和90°时，孔板下游的流场分布较为相似；而倒角角度为45°时，孔板下游流场中轴线位置的高速流体区域较为狭长，外围两侧的漩涡的中心位置基本不变，而末端分离流体的附着点位置向下游移动。当倒角角度为15°和90°时，孔板下游的流场变化较大，使得中心流体的流速迅速增大并达到峰值，并与周围流体发生激烈的动量交换，随后迅速减小后趋于稳定。而倒角角度为45°时，下游的流场变化相对稳定，由于与周围流体的动量交换较少，中心流体的流速在增大到峰值后缓慢降低，流场稳定速度较慢。因此，倒角角度会对孔板下游流场产生一定的影响。

图7是入口流速为0.8 m/s时不同倒角角度孔板下游的速度矢量图。由图7可见：孔板外围的漩涡呈轴对称旋转分布，且在该漩涡的上游、孔板的正后方还存在一个尺度较小的漩涡。随着倒角角度的增大，小漩涡逐渐增大。当倒角角度为45°时，孔板下游的流体流动方向与管道轴线呈现出一定的角度，这减缓了孔板的存在对流场的影响，因此下游流体平均流速较小，流场变化较为缓慢。而当倒角角度为15°和90°时，孔板下游的流体流动方向与管道轴线夹角较小，表明此时倒角角度对减缓孔板影响的作用不明显。

图7 不同倒角角度下孔板下游速度矢量分布图

2.3 FAC速率

取入口流速为0.8 m/s、2.0 m/s和5.0 m/s，分别计算出倒角角度为15°、30°、45°、60°和90° 5种孔板下游的流场分布，并计算出Sh。根据Sh与传质系数的关系，计算出传质系数。

倒角角度为45°时不同入口流速孔板下游的传质系数分布和入口流速为0.8 m/s时不同倒角角度孔板下游的传质系数分布见图8。

图8 孔板下游传质系数分布

由图8可知：当倒角角度一定时，孔板下游传质系数随入口流速的增大而增大；当入口流速一定时，倒角角度从15°变化到90°时，传质系数整体先减小后增大。倒角角度从30°变化到45°再到60°时的变化率远小于从15°变化到30°以及从60°变化到90°时的变化率。由于流体入口流速的增大，轴线位置的流体在相同时间内流到了孔板下游更远的位置，同时加强自身与周围流体的动量交换，传质系数增大，并且峰值向远离孔板的位置偏移。当流体入口流速一定时，倒角角度为45°能减缓孔板对流场带来的变化，下游流场的变化较为平稳，孔口的流体能更好地和周围流体发生动量交换，因此下游的动量交换减小，传质系数减小。当倒角角度小于或者大于45°时，孔板下游流场变化增大，孔口的动量交换减小，下游的动量交换加剧，因此下游传质系数增加。倒角角度的改变对传质系数峰值位置的影响不大。随着倒角角度的增大，传质系数峰值位置远离孔板。

图9为入口流速为0.8 m/s、倒角角度为45°时孔板下游FAC速率分布模拟结果和相同条件下与文献[12]试验结果的对比图。由图9可知，FAC速率的数值模拟结果和试验结果符合较好。与图8所示的传质系数分布相似，FAC速率在孔板下游急剧增加并且在z/d=1.5～2.5处达到峰值；随着下游流动的发展，FAC速率缓慢降低，直至趋于稳定。

图9 FAC速率的数值模拟结果与试验结果对比

图10显示了倒角角度为15°、45°和90°时，孔板下游在3种入口流速下的FAC速率。

图10 不同流速下孔板下游FAC速率模拟结果

由图10可知，孔板下游FAC速率随着入口流速的增大而显著增加。此外，当入口流度从0.8 m/s变化到2.0 m/s时，FAC速率峰值位置无明显变化；而当入口流速度从2.0 m/s变化到5.0 m/s时，FAC速率峰值位置明显向下游移动。这是因为随着流量增大，在流体惯性作用下，动量交换最剧烈的部位向远离孔板的位置移动，所以FAC速率峰值位置向下游移动。

图11为入口流速为0.8 m/s时不同倒角角度孔板下游的FAC速率。

图11 入口流速为0.8 m/s时孔板下游FAC速率模拟结果

由图11可知，随着倒角角度的增大，FAC速率先减小后增大，倒角角度为45°时FAC速率峰值最小。当倒角角度为45°时，孔板下游流场变化较为缓慢，孔口中心流体与周围流体得到充分的动量交换，下游流场变化相对稳定。此时，倒角减缓了孔板对流场的影响，因此FAC速率最小。随着倒角角度的增加，FAC速率峰值位置缓慢向下游移动。对比图10和图11，入口流速对FAC速率的影响更显著。

倒角角度和入口流速均影响了节流孔板下游FAC速率峰值的大小和位置。表2为FAC速率峰值位置随入口流速和倒角角度的变化，表3为FAC速率峰值随入口流速和倒角角度的变化。

表2 FAC速率峰值位置随入口流速和倒角角度的变化

表3 FAC速率峰值随入口流速和倒角角度的变化

结合表2、表3可以看出：当倒角角度为15°时，FAC的高发区位于1.55d～1.70d；当倒角角度为45°时，FAC的高发区位于1.70d～1.85d；当倒角角度为90°时，FAC的高发区位于1.80d～2.00d。当倒角角度从15°变化到45°时，FAC速率峰值逐渐减小，当倒角角度从45°变化到90°时，FAC速率峰值逐渐增大。FAC速率峰值位置随倒角角度的增加向远离孔板的位置移动。

当给定的入口流速一定时，以0.8 m/s为例，当倒角角度从45°变化到60°时，FAC速率峰值的增量较小，相对变化量为1.18%；当倒角角度从60°变化到90°时，相对变化量为5.81%。因此，当倒角角度在45°～60°变化时，FAC速率峰值的变化量小于倒角角度在60°～90°的FAC速率峰值变化量。此外，倒角角度在30°～45°变化时，FAC速率峰值的变化量小于倒角角度在15°～30°的FAC速率峰值变化量。

当孔板出水侧存在一定角度的倒角时，随着倒角角度的改变，流体的流向会发生一定的改变，导致下游FAC速率峰值位置改变；当倒角角度为90°时，其下游FAC速率明显大于倒角角度为30°、45°和60°的孔板；倒角角度为30°、45°和60°的孔板下游的FAC速率比较接近，当倒角角度为45°时，FAC速率最小。