PBM算法在近场爆炸数值模拟中的运用研究*

徐自强，王丽娟，朱 洁，李 闯，宋长杰，时小凡

(1.中煤科工集团 沈阳设计研究院，沈阳 110168；2.沈阳建筑大学，沈阳 110168)

爆炸的成因直接决定爆炸的形式和冲击作用，因此，对爆炸的内部机理和发展过程进行研究显得尤为重要。在研究远场爆炸时，可以假设荷载为自由场中的无限域，进一步利用强冲击荷载作用下的基本方程进行求解，国内外研究人员相继开展大量研究试验，得到较多成果[1]；但研究近场爆炸时，这种假设难以成立，由于其边界情况复杂，导致理论求解极为困难[2,3]，此外，由于近场爆炸破坏力强，约束条件苛刻，受到技术和经济等因素的制约，导致相关试验研究较少[4,5]。为降低经费，并且达到研究目的，采用数值模拟是现在较好的研究手段之一[6,7]。

近场爆炸数值模拟大多采用任意拉格朗日-欧拉算法(ALE)和流固耦合算法。ALE既能保持合理的网格形状，又能准确地描述物体运动，但同时也使计算更加复杂，对方程求解造成困难[8,9]；流固耦合法不需要耦合面上的流体单元和结构单元一一对应，能够大幅减少工作难度，但会造成精度偏低[10]。近年来，逐渐出现新型数值模拟方法，如爆炸粒子算法(Particle blast method，PBM)。PBM基于分子运动理论，能够更好地表征高温下的气体行为，在一定条件下可以更准确的模拟爆炸产物、空气和结构之间的相互作用[11,12]。

为探究PBM算法在近场爆炸问题中的适用性，仿真模拟以T Brvik的AL-6XN不锈钢板近场爆炸试验为依据，对比了ALE、S-ALE和PBM方法的计算精确度和运算效率；采用PBM算法对不同爆心距的钢板近场爆炸工况进行仿真计算，分析了粒子总数和粒子个数比对PBM算法计算精度的影响；通过对150 mm爆心距、球状C4炸药近场爆炸场景进行仿真，分析了不同算法运算时效占比规律。

1 PBM方法理论

PBM是在微粒子法(Corpuscular particle method，CPM)的基础上发展而来的。CPM是一种基于动力学分子理论(Kinetic molecular theory，KMT)的粗粒度多尺寸粒子方法，多用于气体动力学模拟。其中，KMT理论是研究气体粒子及其微观相互作用进而得出宏观气体规律的理论，它源于Daniel Bernoulli的活塞理论，后因麦克斯韦方程的建立，得以广泛运用[13]。

KMT理论基于以下假设：①气体由大量分子构成，这些分子是刚性球状的物体，始终处于随机运动状态；②分子尺寸远小于分子间的平均距离；③分子遵循牛顿运动定律；④分子之间及分子与结构间仅存在弹性相互作用；⑤分子之间不存在排斥力和吸引力。

KMT理论可以准确描述理想气体的各项特性，但计算量巨大，难以在实际模拟中得到运用。为弥补这一缺陷，降低运算量，Olovsson博士提出了将大量分子聚集成一个粒子的方法，即CPM法。但CPM法的下述特征使其无法直接用于爆炸问题模拟：①理想气体定律无法得到绝热膨胀条件下爆炸进程中的急剧压降；②系统处于热平衡的假设无法满足高温高压气体动力学的要求。

PBM改进了CPM，使其可以模拟高温高压下的真实气体规律。PBM算法引入了协体积效应参数，能够更好地反映气体在极端压力下的行为。PBM将许多分子合并为一个微粒，使系统的计算对象数量降低了十几个数量级，见图1。结合增加的计算临界时间步长，这种方法使得模拟宏观系统和长时间问题成为可能。

图1 爆炸粒子法(PBM)(出自文献[13])Fig. 1 Particle Blast Method(PBM)

2 近距离爆炸试验仿真模拟

2.1 试验场景及分析模型

图2 试验装置(出自文献[14])Fig. 2 Test device

图3 试验简图(作者自绘)Fig. 3 Test diagram

表1 AL-6XN钢板近场爆炸试验工况Table 1 Near field explosion test conditions of AL-6XN steel plate

仿真计算采用LS-Dyna有限元软件，分别采用传统ALE法、改进的S-ALE法及PBM法开展仿真模拟。根据试验场景建立1∶1仿真模型，如图4所示。AL-6XN钢板采用全积分壳体单元，网格单元尺寸为7 mm，考虑应变率效应，材料选用关键字MAT_MODIFIED_JOHNSON_COOK来定义，主要参数见表2。夹具为刚体，采用常应力实体单元，网格单元尺寸为10 mm，材料选用关键字MAT_RIGID来定义。

图4 不同的模拟方式Fig. 4 Different simulation methods

表2 AL-6XN钢板材料参数Table 2 Material parameters of AL-6XN steel plate

2.2 PBM仿真计算

根据试验工况，由模型坐标计算得出爆心位置，采用DEFINE_PBLAST_GEOMETRY关键字定义炸药位置及形状特征；采用DEFINE_PBLAST_AIRGEO关键字定义空气域特征；采用DEFINE_PARTICLE_BLAST关键字设置C4炸药材料参数并定义粒子与结构的耦合关系，C4炸药材料参数见表3。基于PBM算法的有限元模型见图3(a)。

表3 C4炸药材料参数Table 3 Material parameters of C4

2.3 ALE与S-ALE仿真计算

作为对照组，建立了基于传统ALE和改进S-ALE的完整有限元模型，见图3(b)及(c)。相较于传统ALE，LS-DYNA中改进S-ALE使用关键字创建流体单元网格，即建模时仅需创建结构有限元网格，简化了建模流程，便于模型的修改处理。ALE和S-ALE的模型尺寸、网格划分方式和单元总数均相同。流体域采用单点积分的ALE多物质单元，轮廓尺寸均为900 mm×900 mm×540 mm。其中，空气视为初始压强100 kPa的理想气体，网格单元尺寸为9 mm，材料选用关键字MAT_NULL定义，密度为1.293 kg/m2，状态方程选用关键字EOS_LINEAR_POLYNOMIAL定义，参数见表4。C4炸药材料选用关键字MAT_HIGH_EXPLOSIVE_BURN定义，状态方程选用EOS_JWL定义，材料参数同表3，状态方程见表5。

表4 空气状态方程参数Table 4 Parameters of air equation of state

表5 C4炸药状态方程参数Table 5 Parameters of C4 equation of state

3 计算结果

3.1 PBM算法计算结果

PBM算法精度与粒子总数N和粒子数量比γ相关，其中N=NHE+NAIR，γ=NHE/NAIR，NHE为炸药粒子个数，NAIR为空气粒子个数。依据模拟经验，每种工况选用6种粒子总数进行模拟，模拟结果见图5。可知当γ不变时，基本上PBM算法精度随着N值增加而提高。但对于不同模型，都存在精度的增幅率随N值增加而衰减的现象。

图5 不同粒子总数下的跨中挠度Fig. 5 Deflection at different particle counts

为研究粒子数量比γ对PBM算法精度的影响，考虑计算精度和时间消耗的情况下，以下述三种工况为基础：①L=150 mm、N=47.5w；②L=200 mm、N=47.5w；③L=250 mm、N=47.5w。每种工况选用5组γ进行仿真模拟。由试算得知三种工况的粒子质量比均为MHE∶MAIR=1∶8.5，其中MHE为初始爆炸粒子总质量、MAIR为初始空气粒子总质量。参考上述粒子质量比设置γ值，模拟结果见图6，可以看出γ对模拟精度的影响十分明显，当γ值接近粒子质量比时，模拟精度较高，γ值偏离粒子质量比时，模拟精度较低。

图6 不同粒子个数比下的跨中挠度Fig. 6 Deflection at different Particle number ratio

3.2 不同模拟算法结果对比

3.2.1 模拟精度方面

对比在PBM、ALE和S-ALE算法下，钢板跨中最终挠度Z、钢板总能量E及CPU运算耗时t，不同模拟工况结果见表6。

表6 不同模拟工况结果Table 6 Results of different simulation conditions

由表6数据可以得出，ALE、S-ALE和PBM算法模拟结果的离散系数分别为0.16、0.20和0.12。由此可知，试验中S-ALE算法模拟结果离散性最大，模拟效果较差；ALE算法次之，但出现了模拟结果小于试验值的情况；PBM算法离散性最小，最大误差不超过20%，模拟效果最好。

此外，爆心距分别为150 mm、200 mm和250 mm时，由PBM算法模拟得到的钢板总能量E(包括动能及变形产生的内能)最大，约为S-ALE算法的1.15倍，约为ALE算法的1.5倍。三种算法得到的E值曲线趋势大致相同，但是，在PBM和ALE算法E值曲线均趋于平稳后，S-ALE算法仍表现出缓慢下降趋势，如图7所示。

图7 钢板总能量Fig. 7 Total energy of steel plate

比例距离不同的三种工况下，ALE算法的平均CPU运算耗时为21 193 s；S_ALE算法的平均CPU运算耗时为19 220 s；PBM算法的平均CPU运算耗时为1919 s。ALE与S_ALE算法CPU耗时相差不多，PBM算法的CPU耗时约为ALE和S_ALE算法的十分之一。由此可知，PBM算法的运算耗时远小于ALE算法和S-ALE算法，具有更高的运算效率。

3.2.2 模拟时效方面

模拟采用戴尔台式工作站，CPU单核基频3.60 GHz，多核心同时工作可超频至4.3 GHz。LS-DYNA求解器为R12_MPP求解器，授权算力为8核芯。L=150 mm工况下，不同算法CPU耗时的帕累托图见图8。

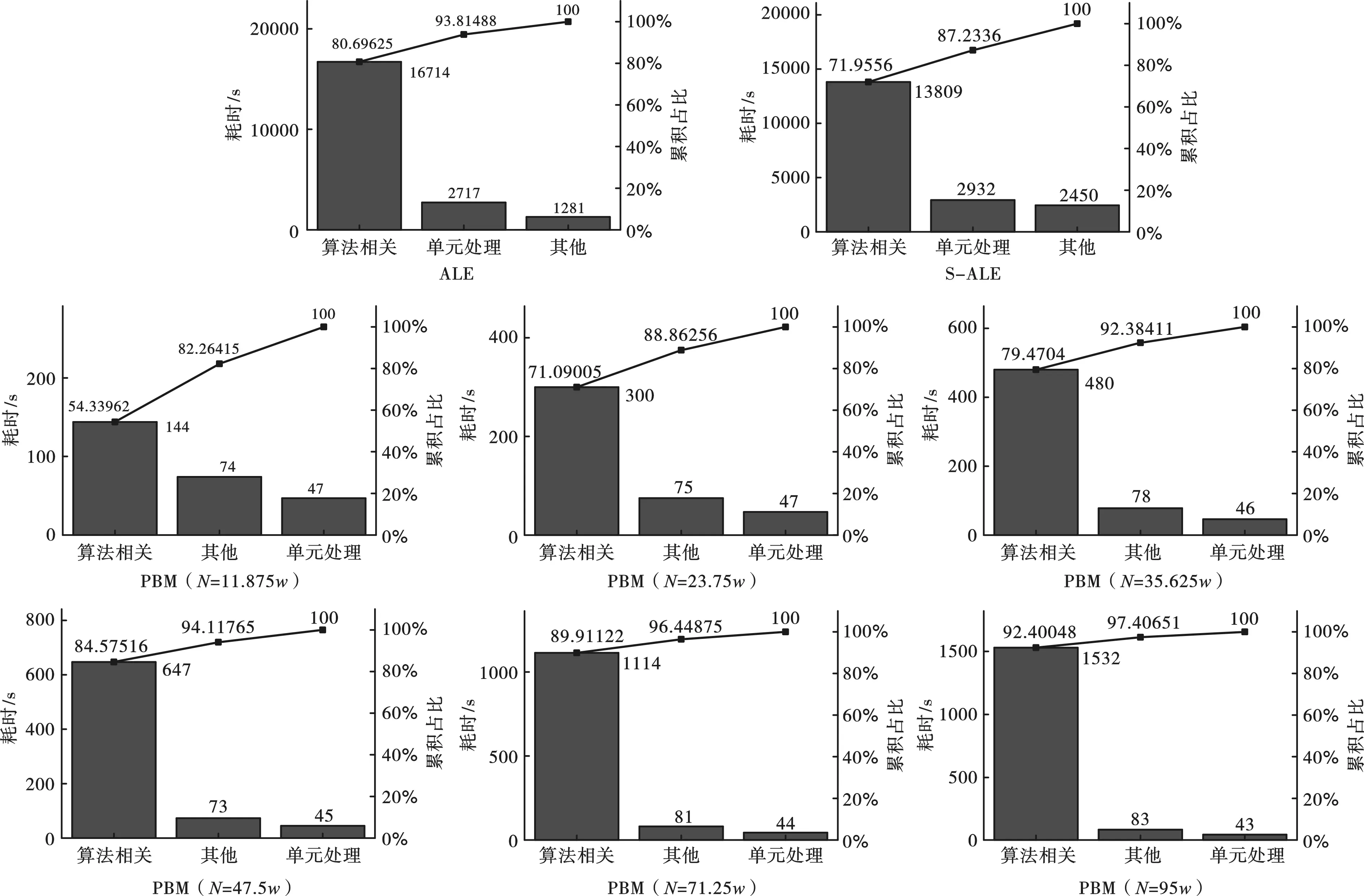
图8 L=150 mm时不同算法CPU耗时占比Fig. 8 CPU time consumption of different algorithms when L=150 mm

对比ALE和S-ALE的CPU总耗时及各处理环节耗时占比，发现S-ALE与ALE的CPU总耗时差距并不明显，但算法相关耗时占比上，S-ALE显著优于ALE，可见改进后的S-ALE算法在算法处理机制上进行了优化，但由于授权核心较少并未有效体现S-ALE在多核心运算上的优势。

对PBM算法而言，粒子总数N对CPU总耗时t影响巨大，两者基本上呈线性关系。PBM算法相关耗时随着N的增加不断增加，占比不断提高，但单元处理和其他耗时基本未发生变化。在可接受的仿真精度范围内，PBM算法效率比ALE和S-ALE算法效率提高10倍以上。

4 结论

(1)PBM方法适用于近场爆炸问题的仿真计算。不同工况下，PBM方法仿真得到的钢板跨中最终挠度与T.Brvik试验结果相近，在最大误差和离散系数上均优于ALE和S-ALE方法的计算结果。

(2)PBM方法精度受粒子量值影响较大。不同工况下，粒子个数比一定时，粒子总数越多，PBM算法模拟精度越高；粒子总数一定时，粒子个数比越接近粒子质量比，PBM算法精度越高。

(3)相同条件下，PBM算法运算效率更高。PBM算法CPU运算用时与粒子总数基本呈线性递增关系。结构单元划分方式与数量相同时，PBM算法的计算用时仅为ALE和S-ALE算法的十分之一，便能得到相同精度的模拟结果。