基于ANSYS/LS-DYNA的工业炸药材料参数标定方法*

2022-03-31张昌锁

爆破 2022年1期

王鑫，张昌锁

(太原理工大学矿业工程学院，太原 030024)

在岩石爆破中，岩石的破坏主要是由于炸药的爆轰作用形成的应力波破坏及爆生气体的准静态作用产生破坏。其中大部分岩石破坏是因为爆生气体渗入裂缝产生的“气楔”作用[1]。因此在数值模拟研究中，较为准确地描述爆轰产物的膨胀做工过程是为岩土爆破设计及优化提供理论指导的关键。

JWL状态方程能够比较地准确描述爆轰产物的膨胀过程中状态参数的变化，不含化学反应，在工程设计中应用较广[2]。JWL状态方程是一种通过试验与计算相结合的半经验状态方程[3]，未知参数由标准圆筒试验法确定[4]。JWL状态方程参数的获得较为繁琐，需要进行不断调整，并且圆筒试验中圆筒很快就会破裂，对于中后期的气体膨胀过程描述不够准确[5]。因此很多学者常利用数值计算与数值模拟结合的方法来确定未知参数。王成利用基因遗传算法根据CJ条件和Hugoniot关系式对炸药爆轰产物γ律状态方程对P-V曲线进行拟合[6]，得到JWL状态方程参数，并利用数值模拟证明了方法的合理性。王言金利用贝叶斯分析方法研究了炸药的不确定参数[7]，并对状态方程进行了贝叶斯参数标定，利用标定参数对平面爆轰驱动飞片试验进行了数值模拟并取得了良好的结果。沈飞等利用圆筒中实验中能量守恒关系及圆筒壁特征位置膨胀速度经验计算公式[8]，建立了一种确定JWL状态方程参数的简便算法，确定了四种常用炸药的JWL状态方程参数，具有良好的拟合效果。李科斌利用水下爆炸实验法结合实验结果[9]，利用Autodyna程序测定了铵油炸药的JWL状态方程参数。目前，状态方程参数标定只能通过少数实验：圆筒膨胀实验、水下爆炸实验、爆轰驱动平板实验及地面挂高爆轰实验，且一种实验标定的状态方程不能用另一种实验来验证。很少文献通过两种不同的爆轰实验来验证参数的准确性，对于JWL状态方程参数调整没有依据。工程爆破中对于炸药要求具有一定的猛度、爆力，但在大多数爆破设计数值模拟过程中，缺少对于炸药材料爆力、猛度指标的验证。

本文基于ANSYS/LS-DYNA有限元软件，针对工程中常用的CHNO型炸药，使用一种简便算法得出JWL状态方程的未知参数，将该参数作为原始参数。以工业炸药的爆力、猛度性能指标为标准，对铅柱压缩试验、铅铸扩孔试验进行数值模拟，通过两种不同的实验来检验计算参数的准确性并根据数值实验结果对于计算参数进行调整修正。为岩石爆破数值模拟研究提供一种快速确定工业炸药参数的方法。

1 JWL状态方程参数计算

JWL状态方程的标准形式及等熵形式为[10]

(1)

PS=Ae-R1V+Be-R2V+CV-(ω+1)

(2)

式中：P爆轰产物压力；V为爆轰产物的相对体积；E为爆轰产物单位体积的内能。式中共有A、B、C、R1、R2、ω六个未知参数。

炸药在爆轰的过程中满足CJ爆轰条件，可以得到一组方程式，代表CJ爆轰条件对于JWL状态方程中未知参数的约束

(3)

(4)

(5)

式中：VCJ是CJ点处爆轰产物的相对体积；ρ0是炸药的初始密度；D是炸药的爆速；PCJ是CJ点处的爆轰产物压力；ECJ为CJ点的爆轰产物的内能。

对于凝聚态炸药，在CJ点处有

(6)

(7)

(8)

式中：ρJ为CJ点处爆轰产物的密度；r是爆轰产物的多方指数，与炸药性质有关，对于高密度的凝聚态炸药r通常取3[11]。文献[12]提出一种适用于混合炸药的经验公式，具体形式如下

(9)

将式(6)、(7)、(8)分别带入到式(3)、(4)、(5)中，便可以得到未知参数A、B、C、R1、R2、ω同炸药密度ρ0和爆速D之间的关系。

根据大量实验证明，R1、R2、ω并非是相互独立的变量，R1、R2、ω的取值范围分别为[4,7]、[0.8,2]、[0,1][13]。此外根据文献[14]对于CHNO型炸药，ω一般取0.33，且R1与R2有类线性关系，R2=0.27R1，所以仅需要在[4,7]的范围内选取R1的值便可以对A、B、C进行求解。

得到一组未知参数A、B、C的解之后就需要对于解的正确性进行判断。选择标准圆筒试验中爆轰产物比容为2.4和7.0的函数值是否接近于零来判断解是否符合要求。

(10)

式中：u为圆筒特征处的速度值；ρm为圆筒材料的密度；ρm=8.93 g/cm3；ri0和re0分别为圆筒的初始内外径，ri0=12.7 mm,re0=15.2 mm;E0是能量计算中的一个基准值，对于大多数的凝聚态炸药根据文献[15]，有

E0=(0.204-0.0734ρ0)ρ0D2

(11)

对于特征处的速度值，文献[8]提出一种较为准确的经验计算公式

(12)

(13)

计算程序图如图1所示，∈为极小正实数。

图1 计算程序图Fig. 1 Computational Diagram

2 数值模拟

2.1 材料参数选取

采用关键字*MAT_HIGH_EXPLOSIVE_BURN和关键字*EOS-JWL来描述炸药材料及爆轰产物的状态方程。对于2#岩石乳化炸药，产品说明书主要性能指标如表1所示。采用上文中的计算方法，利用MATLAB软件编写计算程序，计算JWL参数，得到的材料参数如表2所示。

表1 2#岩石乳化炸药主要性能指标Table 1 Main performance index of 2 # rock emulsion explosive

表2 2#岩石乳化炸药材料计算参数Table 2 Material calculation parameters of 2 # rock emulsion explosive

铅采用Johnson-cook本构模型及Gruneisen状态方程描述，其具体形式如下

(14)

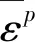
(γ0+αμ)E

(15)

式中：μ=ρ/ρ0-1；α为γ0的体积修正系数；C0、Si、γ0为状态方程中的常数。具体参数值见表3所示。

表3 铅材料参数Table 3 Lead material parameter

2.2 数值模型建立

2.2.1 铅柱压缩实验

铅柱压缩法，是测定炸药猛度的一种方法。在钢板中央放置φ40×60 mm的铅柱，铅柱上放置φ41×10 mm圆钢板，钢板上放50 g炸药，包装成直径d=40 mm纸筒，放入雷管，把药筒与钢板固定好。引爆后，铅柱压缩的高度，用mm表示的值称为该炸药的猛度[16]。为了保证计算的准确性，采用同试验参数相同的设置。利用ANSYS软件前处理建立三维计算模型，采用1/4建模，模型尺寸为：铅柱φ40×60 mm，钢板φ41×10 mm，炸药φ40×30 mm，装药量为50 g。采用多物质流固耦合(ALE)算法进行模拟，空气部分φ60×100 mm，划分网格采用均匀网格划分，网格大小为1 mm，单元总数为262080。起爆位置为装药中心，数值模型如图2所示。

图2 铅柱压缩计算模型图Fig. 2 Calculation model diagram of lead column compression

2.2.2 铅铸扩孔实验

铅铸扩孔实验是测定炸药做功能力的一种方法。系将10 g炸药置于圆柱形铅铸中央的孔中(铅铸直径及高均为200 mm，孔径25 mm，深125 mm，用细石英砂填充到孔口。引爆炸药后，爆轰产物将孔扩张为梨形，测量孔的扩张体积，以此衡量炸药的做功能力[17]。为了保证计算的准确性，采用同试验参数相同的设置。

利用ANSYS软件前处理建立三维计算模型，采用1/4建模，模型尺寸为：铅铸φ200×200 mm，孔径为25 mm，孔深为125 mm，炸药装药高度为20 mm，装药量为10 g。采用多物质流固耦合(ALE)算法进行模拟，空气单元设置底部大小与模型等大，高度为模型高度的1.5倍，划分网格采用均匀网格划分，网格大小为2 mm，单元总数为136540。起爆位置为装药中心，数值模型如图3所示。

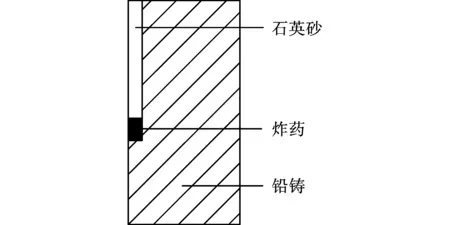
图3 铅铸扩孔模型图Fig. 3 Explosion power test model

2.3 数值模拟结果

2.3.1 铅柱压缩实验模拟结果

利用后处理软件LS-PrePost对于数值模型进行轴对称处理，铅柱压缩过程的变形云图，如图4所示。在炸药起爆后，爆轰波从装药中心向四周扩散。冲击波压力通过钢板传递到铅柱的上表面，铅柱开始压缩。当压力达到铅柱材料的屈服强度后，铅柱塑性变形急剧增长，由于刚性地面的作用，压力无法传递，铅柱上表面出现扩散状变形。随着压缩的进行，铅柱上表面逐渐出现“蘑菇状”卷曲。

图4 铅柱压缩过程变形云图Fig. 4 Deformation cloud image of lead column during compression

在整个铅柱压缩过程中，钢板的变形量极小，因此在钢板的不同位置取点，记录钢板z方向上的位移量作为铅柱压缩量，绘制铅柱压缩量-时间曲线如图5所示。对应测点的z方向上测点的速度-时间曲线如图6所示。

图5 压缩量-时间曲线图Fig. 5 Compression-time graph

图6 测点速度-时间曲线图Fig. 6 Velocity-time curve of measuring point

炸药起爆后，铅柱在40 μs左右达到了最大压缩速度，之后随着时间的增长压缩速度逐渐减小，并在800 μs时接近于0，800 μs之后铅柱的压缩量基本不再变化，认为铅柱压缩过程完成。

2.3.2 铅铸扩孔试验模拟结果

利用后处理软件LS-PrePost对于数值模型进行轴对称处理，观察铅铸扩孔过程，其变形云图如图7所示。随着炸药的起爆，爆生气体迅速膨胀，以近似球面的形式作用于铅铸孔壁以及堵塞材料上，早期爆腔的形状基本为球形。随着爆生气体的膨胀，爆生气体的压力也在不断减小，爆腔的扩张速度也逐渐减慢。铅铸底部为刚性地面，且石英砂堵塞装填密度较低，铅铸内孔逐渐被扩张为梨形,上表面内孔边缘出现了一定尺寸的凸起。

图7 铅铸扩孔过程变形云图Fig. 7 Explosion power test deformation nephogram

铅铸扩孔数值模拟的结果，由于后处理软件LS-PrePost无法对于扩孔空腔进行直接的体积测量，所以需要对数值实验结果进行二次处理。利用LS-PrePost对于铅铸扩孔结果模型沿着不同径向进行切分，输出扩孔空腔边缘各节点坐标，利用ANSYS前处理软件，对于空腔进行重建，生成K文件，利用LS-PrePost测量重建空腔模型的体积。测量不同时间的空腔体积绘制空腔体积—时间曲线如图8所示。取空腔边缘具有代表性的测点，绘制速度-时间曲线图如图9所示。空腔体积的增长速度在随着时间的推移逐渐减小。在1000 μs左右，空腔体积基本上不再变化，扩孔过程基本完成。

图8 空腔体积-时间曲线Fig. 8 Cavity volume-time curve

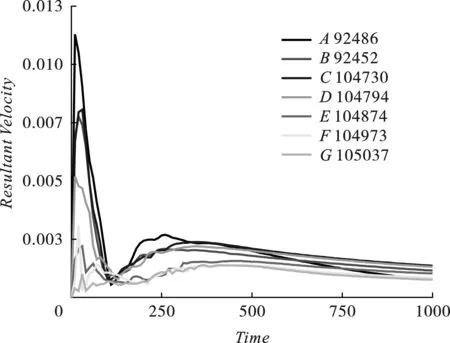
图9 测点速度-时间曲线图Fig. 9 Velocity-time curve of measuring point

3 数值模拟结果分析

对于不同方向上测得的空腔体积求平均值，得到铅铸扩孔数值实验的结果，测得的铅铸扩孔体积为335.053 mL。铅铸扩孔实验测得的炸药爆力值按下式计算

X=(V2-V1)(1+K)-22

(16)

式中：X为炸药的爆力值，mL；V1为起爆前铅铸内孔的体积，mL；V2为起爆后铅铸扩孔空腔的体积，mL；K为温度修正系数，实验室温为20℃，K=-2%。

按照2#岩石乳化炸药说明书爆力值280 mL，代入式(16)中计算得，起爆后铅铸扩孔空腔的体积为369.51 mL，数值模拟结果的误差为9.3%，满足要求。

对于铅柱压缩数值模拟结果，铅柱压缩量可以直接通过测量钢板位移量来确定。经过测量，铅柱压缩量为13.08 mm。按照2#岩石乳化炸药说明书压缩量16 mm计算，数值模拟实验结果的误差为18.25%，超过了15%，误差较大，所以需要对参数进行修正。

PS=Ae-R1V+Be-R2V+CV-(ω+1)

(17)

在JWL状态方程中，第一项控制高压段，第二项控制中压段，R1、A为高压段控制参数，R2、B为中压段控制参数。以计算的得到的2#岩石乳化炸药JWL状态方程参数为原始参数集，控制其他参数不变，将A、B、R1、R2作为因素，设置三个水平，进行正交试验，对这四个参数进行敏感性分析并确定相应的参数调整方向，正交试验表及结果如表4所示。

表4 正交试验表及结果Table 4 Orthogonal numerical test scheme and results

对正交试验结果进行方差分析(F检验)，以起爆后空腔体积表征爆力，铅柱压缩量表征猛度。试验因素及误差的自由度分别为2和6，当显著性水平分别为α=0.05、α=0.01时，查表可知F临界值为5.140、10.90；计算得出试验因素的F比如表5所示。

表5 试验因素F值表Table 5 Test factor F value

当试验因素值小于10.90，大于5.140时，认为该因素对于结果影响比较显著；当试验因素F值大于10.90时，认为该因素对于结果影响十分显著；并且F值越大表明对于结果的影响也就越显著。通过表4、5分析JWL状态方程中的四个参数变化对于结果的影响：

(1)爆力对于参数R1的变化较为敏感，并且扩孔空腔体积随着参数R1的减小而增大；对于剩余的三个参数敏感性A⟩R2⟩B，铅铸扩孔空腔体积分别随着参数A、B、R2的增大而增大。

(2)猛度对于参数R1的变化极为敏感，并且压缩量随着参数R1的减小而增大；对于剩余的三个参数敏感性A⟩R2⟩B，压缩量分别随着参数A、B、R2的增大而增大。

(3)猛度对于参数R1的敏感性明显强于爆力。

猛度表征炸药对于接触介质的破坏能力，反映的是炸药瞬间爆轰释放的能量，主要受爆速及爆轰压力影响。但从正交试验结果来看，猛度也与爆生气体作用有关，体现在猛度对与JWL状态方程高压段参数R1、A的敏感性上。相较于猛度，爆力对JWL状态方程高压段参数R1、A的敏感性较弱，因为爆力反映的是爆生气体膨胀做功的能力，受爆生气体整个膨胀过程的影响。爆生气体作用时间较长，受JWL状态方程参数A、B、R1、R2的协同作用影响。

对于炸药材料参数的修正，主要修正JWL状态方程中的四个参数A、B、R1、R2，其余参数的计算公式经过前人大量的验证大多误差不超过3%。对于A、B、R1、R2的修正，结合爆力、猛度对于参数的变化关系，先匹配猛度值，率先确定R1、A，再匹配爆力，确定R2、B的值。必要时可采用插值的方法，将爆力、猛度结果误差控制在5%以内。

修正后的2#岩石乳化炸药材料参数如表6所示。