爆破冲击荷载作用下宏观孔隙混凝土损伤演化的近场动力学模拟*

梁志坚，吴 亮，杨旭风，周俊汝

( 武汉科技大学 理学院 湖北省智能爆破技术研究中心,武汉 430065)

众所周知，混凝土、岩石等材料内部包含大量不规则、跨尺度的不连续微结构(如孔隙、空洞或裂隙等),在外荷载作用下，这些随机分布的宏观裂隙会扩展、汇聚，而孔洞周边也会萌生新的裂纹，最终导致材料的破坏。为此，许多学者首先对预制的单圆孔岩石试样进行了大量的研究[1-4]，但是混凝土、岩石中孔洞的数量庞大，且微结构数量多、形态复杂且无序分布，仅通过单个或多个孔洞的试验研究宏观孔隙对混凝土与岩石力学特性的影响是非常困难的，并且试验结果也具有很大的离散性。

尽管近年来国内外学者通过实验与模拟技术对含孔隙岩石、混凝土的静力学与动力学特性进行了探讨[5-12]，取得丰硕的成果。但以往的数值模拟大都使用基于有限单元法或有限差分法的计算机软件来模拟裂纹的扩展，这些软件必须预先定义混凝土或岩石的破坏准则，而且为了能够模拟混凝土或岩石的非连续性而不得不采用大量的假设，进而导致采用不同破坏准则和不同假设得到不同试验结果的现象[13]，另外，由于混凝土孔隙的离散性、复杂性以及统计分布函数特征的局限性，从理论上建立的本构模型在表达材料全应力应变本构关系中存在一个共性的不足，即对于初始含有宏细观缺陷材料在应力环境中的耦合机制不明确[14]。初始宏细观损伤对混凝土的力学响应特性不同，因此有必要展开初始存在宏细观缺陷对混凝土的力学响应机制研究。近场动力学能够很好模拟混凝土连续性问题，通过颗粒间的微观力学参数来表现材料的宏观力学行为。

本文利用三维随机球模拟宏观孔隙混凝土的孔隙，提出了随机球的生成与随机投放算法，建立了宏观孔隙混凝土的三维模型，并开展了静载和冲击荷载作用下宏观孔隙脆性材料的变形、破坏和能量耗散等方面的分析。

1 基于键的近场动力学理论

1.1 运动方程

近场动力学基本理论是将介质离散为空间中一系列的物质点，每一个物质点与其一定相邻范围内的其他物质点存在相互作用，并通过空间积分方程来刻画材料的力学行为，其本质是通过求解空间中各物质点的运动状态来反映材料的宏观变形。在近场动力学中，将物质点之间的这种相互作用称为键。

假定介质内任一点x，受到其半径为δ的邻域Hx内的另一质点x′的影响，如图1所示。当介质受力产生变形后，x和x′质点将移动到新位置，它们之间将产生一对相互作用力f，定义为对点力，该力与质点间的相对位置和位移相关。根据牛顿第二定律，质点x的运动方程表示为

图1 材料某质点邻域内的键和对点力Fig. 1 The bond in the material and point-to-point force

ρ(x)ü(x,t)=fHxf(η,ξ)dV+b(x,t)

(1)

式中：ρ为材料密度；u为质点位移向量；ü(x,t)为质点加速度向量；η=u(x′,t)-u(x,t)为质点相对位移；ξ=x′-x为质点相对位置；b(x,t)为外体力密度。

1.2 近场动力学中的材料模型

近场动力学理论不同于传统连续介质力学，其特点是采用键的伸长率以及质点之间的相互作用力来刻画介质的本构关系，而不是采用应力与应变的方式描述。

(2)

式中：c为键常数；s为键的伸长率。

Silling通过建立近场动力学与经典连续介质理论的能量方程之间的相互联系[15]，从而导出了各向同性的微弹性脆性介质的键常数

(3)

式中：κ为体积模量；δ为近场域半径。

2 数值计算方法

在进行数值模拟时，通常将模型离散成均匀分布在正方形网格中心的一系列质点，如图2所示，网格边长为Δx，每一个质点代表了其所在的网格区域，体积为Δx3。质点的近场半径一般取δ=3Δx，质点xi与其近场域Hxi内的任一质点xk通过键相互连接，近场域内的质点数为NHxi。

图2 物质空间离散化示意图Fig. 2 Schematic diagram of material space discretization

通过考虑每个质点xk在质点xi近场域内的总体积来近似表示近场域内的数值积分，离散后的近场动力学方程为

(4)

式中：Vk为质点xk的体积，在近场域边缘处，xk在近场域内的体积会减少。

离散后的近场动力学方程为

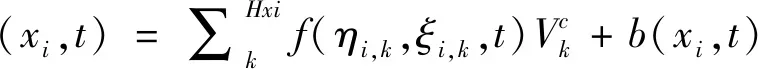
(5)

近场动力学方程采用时间积分，一般采用中心差分法。由于近场动力学方法是一种动态的动力学算法，其静力学问题的解则是动态响应的稳定部分。因此，当需要计算静态或者准静态问题时，需要将动力松弛法引入到近场动力学方程中[16]。Kilic和Madenci首次将自适应动态松弛方法引入到了近场动力学中[17]，优化了静态或者准静态问题的计算。

3 宏观孔隙混凝土单轴压缩实验

3.1 试件制备

实验中采取用C30水泥与黄沙材料制备试件，其中水泥、黄沙、水的比例为2∶1∶0.65，制备后的无孔隙试件平均密度为2026 kg/m3。为制备含不同孔隙率的混凝土试件，利用聚苯乙烯小球来获取孔隙(聚苯乙烯的熔点低、密度轻、强度低，是一种很好模拟孔隙的材料)，不同的孔隙率采用投放的聚苯乙烯小球数量来控制，而不同粒径的孔隙用聚苯乙烯小球的尺寸来控制。试样制作过程中首先按确定的水泥、黄沙、聚苯乙烯小球以及水的比例配比好后，通过搅拌使孔隙分布均匀，见图3，随后倒入PVC管养护3 d后脱模，再将试件养护28 d后放入烤箱，通过合适的温度融化聚苯乙烯小球，其中烤箱控制温度在165℃～175℃之间(混凝土材料在180℃高温以下其力学特性不受影响)，恒温保持2.5 h，待聚苯乙烯小球融化从而获得符合实际的孔隙结构，见图4所示。试样CT扫描采用武汉康明斯燃油系统有限公司设备及系统见图5，试样CT扫描剖面图见图6。

图3 制备孔隙试件的材料Fig. 3 Materials for preparing porous specimens

图4 孔隙混凝土试件Fig. 4 Porous concrete specimen

图5 CT扫描系统Fig. 5 CT scanning system

图6 试件CT扫描图Fig. 6 CT scan of specimen

3.2 实验结果

宏观孔隙混凝土试样的单轴压缩实验结果见表1。实验结果显示：随着孔隙率的增加，试样的密度、抗压强度、弹性模量以及纵波波速不断降低，数据表明孔隙率对宏观孔隙混凝土材料力学性能的影响显著。

表1 不同孔隙率试件的力学性质参数Table 1 Mechanical property parameters of specimens with different porosity

图7、图8为不同孔隙率下混凝土试件单轴压缩的主应力应变曲线图。其中，图7中孔隙率差值为5%，图8中孔隙率差值为10%。宏观孔隙混凝土试件压缩实验结果显示：当位移荷载加载过程中应变ε达到0.00178时，宏观孔隙率为零的试件抗压强度达到最大，其值为32.33 MPa；当宏观孔隙率由0%增加到5%时，试件的抗压强度下降到前者的一半以上，其值为15.42 MPa，此孔隙率段下降程度显著；当孔隙率在5%～20%区间时，试样抗压强度与孔隙率近似呈线性负相关，其中当孔隙率每下降5%，试样的抗压强度下降约3 MPa；当宏观孔隙率达到30%后，孔隙率对抗压强度影响减弱，同时试件在应力峰值前均有不同程度的应力跌落现象，这是由于孔隙试件在加载过程中发生局部破坏而释放能量，使得抗压强度峰值瞬间下降[18]，但由于材料仍然存在一定的承载力，继续加载应力又将继续上升，直至破坏(宏观表现为试件两端被压溃，孔隙球洞塌陷且伴有大块度的混凝土滑移甚至剥落)。声波测试表明：随着宏观孔隙率的增大，混凝土试件的纵波波速随之减小。

图7 不同孔隙率主应力-应变曲线Fig. 7 Principal stress-strain curves with different porosity

图8 不同孔隙率主应力-应变曲线Fig. 8 principal stress-strain curves with different porosity

3.3 单轴压缩近场动力学模拟

几何参数：圆柱的直径D=5 cm，其高度H=10 cm。材料属性：弹性模量E=21 GPa，泊松比v=0.25，密度ρ=2.02 g/cm3。边界条件：上端边界条件：θz=1×10-6m/s，下端边界条件θz=-1×10-6m/s。近场动力学离散参数：X方向与Y方向质点总数均为50个，Z方向质点总数106个，质点间距Δ=0.001 m。单个质点体积：ΔV=1×10-9m3。虚拟边界层体积：ΔVδ=3×53×53×ΔV=8.427×10-6m3。临界伸长率(考虑损伤)：Sc=3.1×10-4。时间步长Δt=1.0 s。使用自适应动态松弛法，总时间步数为1000。模型孔隙粒径2.5 mm，宏观孔隙率大小分别为0%、10%、20%、30%、40%六种工况，当孔隙率为20%时。孔隙20%试件的近场动力学模型见图9。

图9 孔隙20%试件的近场动力学模型Fig. 9 Peridynamic model of 20% void specimen

图10为近场动力学模型计算与压缩实验位移-荷载的对比曲线。孔隙混凝土宏观力学性能依赖于基体材料的力学性能和随机分布的孔隙。孔隙混凝土与孔隙率为零的混凝土试样相比，含孔隙试样的峰值强度显著降低，降低程度与孔隙率大小以及粒径尺寸有关的微观机理分析表明：孔洞周边裂纹的萌生与扩展过程伴随着应力集中区的释放与转移。结果对比表明：近场动力学模拟与实验结果的吻合性较好，从而说明近场动力学方法可为进一步探究宏观孔隙岩体的力学性能提供有效的计算手段。

图10 不同孔隙率下位移-荷载曲线Fig. 10 Displacement load curve with different porosity

4 冲击荷载下宏观孔隙混凝土损伤演化模拟

上节对不同孔隙混凝土试样进行了近场动力学模拟，且通过试件压缩实验结果验证了近场动力学计算模型及参数的可靠性。众所周知，混凝土中能量耗散依赖于许多因素，不仅与混凝土孔隙率有关，而且还受到混凝土强度等级、混凝土的颗粒大小、胶结程度、饱和程度等的影响。为了研究混凝土孔隙率对能量耗散的影响，需要保证其他条件基本一致。本节对孔隙混凝土试样施加冲击荷载，研究不同孔隙率以及孔隙粒径尺寸对孔隙混凝土试样损伤演化过程的影响。为简化计算，爆破荷载采用三角形荷载，荷载峰值为60 MPa，荷载上升时间长0.01 ms，荷载下降时间段长0.09 ms。其他参数采用4.3节参数。

不同孔隙率及不同孔隙粒径的混凝土试件损伤演化过程见表2、表3。宏观孔隙率为零的混凝土试样在冲击荷载作用下具有明显的压剪破坏形式，主要是试件未加围压约束，晶体颗粒在轴向冲击压缩下产生侧向移动，而含孔隙的混凝土由于试件中预制了大量的孔隙，在冲击载荷作用下发生孔隙间混凝土骨架的拉伸或剪切贯通破坏；表2、表3显示混凝土试件的损伤演化过程是从加载端部开始产生压缩变形与剪切破坏，并逐步向支承端传递。

表2 不同孔隙率混凝土试件损伤演化过程Table 2 Damage evolution process of concrete specimens with different porosity

表3 不同孔隙粒径混凝土试件损伤演化过程Table 3 Damage evolution process of concrete specimens with different pore sizes

当应力波通过含孔隙介质时，由于孔隙是空的，没有介质来传递应力波，应力波需要消耗很多能量绕过这些孔隙并继续传播，所以空孔隙将耗散应力波的能量。另外，宏观孔隙混凝土破坏过程中的能量耗散特性与其内部损伤特征有十分密切的联系，作用于孔隙混凝土的外部能量是产生孔隙混凝土内部损伤破坏的直接原因，由于裂纹的孕育、繁衍、萌生、扩展和贯通每一阶段都要从外部吸收能量，而且是不可逆的能量耗散过程。同时，试件相同剖面位置上的有效承载面积随着孔隙率的增加而降低，意味着混凝土骨架结构的动应力加大，更易损伤破坏，这也进一步反映出混凝土孔隙率的增加使得能量耗散进一步加剧。混凝土试件孔隙率不同，其抗压强度也不同，混凝土孔隙率越大，其抗压强度就越小，因此在相同冲击荷载下不同孔隙率混凝土的破坏情况不同，孔隙率大的孔隙混凝土试样破坏严重。相关研究表明[8]，随着孔隙率的增加，剪切破坏区的扩展范围及长度也相应减少。这说明混凝土试件的孔隙率越大，其相应的破坏范围减少，孔隙率对冲击载荷作用下混凝土试件能量耗散起着重要作用；由于本文混凝土试件长度短，且底部约束，因此，试件在冲击载荷作用下，其剪切破坏区的扩展范围及长度随着混凝土试件孔隙率的增加而增加。如果增大模型尺寸范围，一定的冲击荷载条件下，增大孔隙率将消耗更多的能量从而降低远区介质的损伤与破坏范围，当然也需综合考虑介质强度随孔隙增加而降低的因素。

5 结论

针对静载、冲击荷载条件下宏观孔隙混凝土的孔隙参数对混凝土损伤演化过程的影响问题，本文基于蒙特卡罗方法，采用MATLAB程序生成随机孔隙结构的物理模型，通过自编近场动力学程序模拟了单轴压缩下宏观孔隙混凝土的应力应变过程，并结合以聚苯乙烯小球高温融化为孔隙体的混凝土试件，进行了单轴压缩实验，并验证了近场动力学计算结果的准确性，随后模拟了爆破冲击作用下宏观孔隙混凝土的裂纹萌发与扩展。得到了以下结论：

(1)轴向压缩实验结果表明孔隙率对宏观孔隙混凝土材料力学性能的影响显著，混凝土的密度、抗压强度、弹性模量以及纵波波速与孔隙率成反比。另外，近场动力学模型的计算结果与实验数据相吻合。

(2)宏观孔隙混凝土存在大量的孔隙结构，冲击载荷作用下混凝土骨架结构的动应力增大，因此孔隙间混凝土骨架更易在动拉应力或剪切作用下贯通破坏。

(3)在相同冲击强度下不同孔隙率混凝土呈现的破坏程度不同，主要是孔隙率对冲击载荷作用下混凝土试件能量耗散起着重要作用，因此孔隙率大的孔隙混凝土试样破坏严重。