页岩气水平井生产压降计算新模型

谢南星， 蔡道钢， 叶长青， 唐寒冰， 王庆蓉， 杜明海

1中国石油西南油气田分公司工程技术研究院 2中海油田服务股份有限公司

0 引言

页岩气水平井通过体积压裂改造，大量压裂液进入地层，由于页岩基质渗吸作用，生产初期地层压裂液返排率较低，生产中后期压裂液通过裂缝逐步流入井底，导致页岩气水平井全生命周期均或多或少的产水。

页岩气井普遍产水导致井筒中存在气水两相流动，两相流动是人工举升工艺设计分析的基础。两相流动的压降和持液率变化规律非常复杂，准确认识井筒压力和持液率分布对页岩气井日常生产优化和生产动态分析都具有重要作用[1- 4]。气水两相流压降计算模型主要为经验模型，由Duns & Ros[5]基于实验测试不同气液速度准数的压力梯度得到。Hagedorn & Brown[6]通过457.2 m实验井压降测试得到适用于305 mm和76.2 mm管径的压降计算相关式。Orkiszewski[7]提出不同流型混合物密度和摩阻压力梯度的计算方法，并使用148口井的压降测试数据对前人模型进行了优选和分析。Beggs & Brill[8]首次提出考虑任意倾斜角的压降计算模型，Mukherjee & Brill[9]在Beggs & Brill工作基础之上改进实验条件，进行了0～90°范围内的实验测试，提出气液两相倾斜管流的持液率及摩阻系数经验公式，结合任意倾斜角的压降计算模型，得到了适用于水平、倾斜和垂直井的压降计算模型，之后的压降计算模型都是在这些模型基础之上进行的改进和完善[10]。

压降计算模型的准确度与持液率、摩阻以及流型判断密切相关，各个模型在不同气井条件下的计算准确性不同。文章利用长宁区块的现场测试数据对常用的压降计算模型进行了分析和评价，并通过优化泡状流、段塞流和环雾流流态转变界限和引入分层流压降的方法，建立了页岩气水平井压降计算新模型，通过对比实测数据验证了模型的准确性，并使用该模型对页岩气水平井井筒流态分布和变化进行了分析。

1 井筒压降计算方法评价对比

常用的四种压降计算模型的基本原理和适用范围如表1所示。

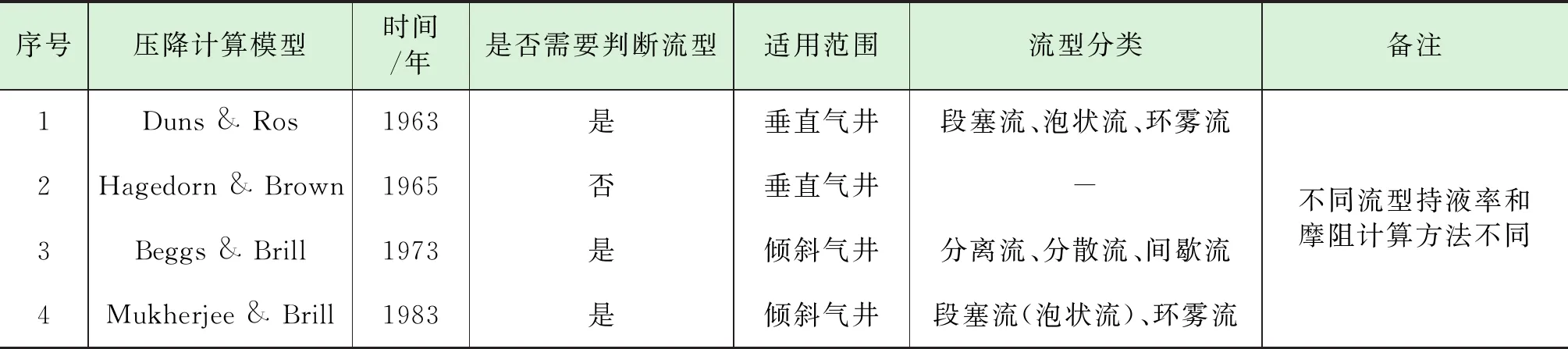
表1 常用压降模型原理和适应范围表

Duns & Ros和Hagedorn & Brown是垂直井压降计算模型，而页岩气主要以水平井的方式生产，所以本文使用Beggs & Brill(B-B模型)和Mukherjee & Brill(M-B模型)这两种压降计算模型进行对比分析。

2020年6月～7月期间进行了流动压力测试的长宁区块页岩气水平井基本信息，以及B-B模型、M-B模型压降计算结果和误差分析如表2所示，这些井产气量在2×104～10×104m3/d之间，产水量在1～30 m3/d之间，现场压力测试计最多下入到A靶点附近，测试得到的压力梯度曲线未见明显拐点，表明这些井在A靶点位置之上未见积液。

从表2可以看出，在产水量都为1 m3/d的情况下，产气量在3×104～6×104m3/d时，M-B模型的平均相对误差为4.50%，B-B模型相对误差为23.53%；新模型相对误差为2.83%;产气量在5×104～10×104m3/d时，M-B模型的平均相对误差为7.07%，B-B模型平均相对误差为3.80%；新模型相对误差为4.03%;产水量大于8 m3/d条件下，M-B模型的平均相对误差为6.86%，B-B模型平均相对误差为9.59%,新模型相对误差为5.96%。计算结果表明M-B模型在小气量和大水量条件下较适合，B-B模型在大气量下更为合适。

表2 井底压力计算典型井基本信息表和误差分析

M-B模型流态划分中主要划分为泡状流、段塞流和环雾流、泡状流和段塞流。误差对比结果表明，M-B模型对于泡状流、段塞流的井筒摩阻和持液率经验模型更合理，使得M-B模型对高持液率条件下井筒压降计算较为准确。B-B模型流态划分为分离流、分散流和间歇流，B-B模型对环雾流条件下的流态划分更为详细，使得B-B模型在计算气井低持液率条件下更具有优势。对于水平井，目前普遍认为井筒中除了泡状流、段塞流和环雾流以外，还存在分层流，但这两种压降计算模型中均未对该流态进行划分，也未考虑该流态的持液率和摩阻计算模型。通过对泡状流、段塞流、环雾流和分层流四种流态的流型转换界限进行优化，并在压降模型中考虑分层流摩阻和压降的方式，提高压降计算模型适用范围和准确性。

2 页岩气水平井井筒压降新模型

2.1 压降梯度方程

目前所有的垂直管压降模型中，均用式(1)计算井筒压降：

(1)

式中：p—井筒压力，MPa；Z—井深，m；ρm—混合物密度，kg/m3；g—重力加速度，m/s2；fm—摩阻系数，无因次；Gm—气液混合物质量流量，kg/s；D—油管内径，m；A—油管内表面积，m2。

而对于倾斜管，考虑角度的压降计算公式为：

(2)

式中：θ—井斜角，(°)；vm—混合物速度，m/s。

不同气液流速对应井筒不同流态，准确划分流态和计算不同流态下的持液率和摩阻系数fm,有助于提升井筒压降模型的准确度。

2.2 流型转换界限方程

本文提出考虑气液密度、流速和表面张力的速度准数：

(3)

(4)

式中：Nvsg—考虑气液密度、流速和表面张力的气相速度准数，无因次；NvsL—考虑气液密度、流速和表面张力的液相速度准数，无因次；σ—气水表面张力，N。

2.2.1 泡状流—段塞流

泡状流向段塞流过渡是泡状流中的空隙率增加导致的，随着气体流速的增加，泡状流中的气泡碰撞、聚集速度增加，形成气泡团或者帽状气泡，然后进一步向泰勒气泡转变，最终转化为段塞流。

基于AESR[11]、Mukherjee[12]、Mauricio[13]、Barnea[14]以及Taitel[15]的实验数据，使用麦夸特法结合通用全局优化法对上述流型转换界限实验数据进行拟合，可得到全角度下的流型转换界限方程为：

(5)

2.2.2 段塞流—环雾流

随着气量增加，井筒中持液率降低含气率增加，段塞流逐渐向环雾流过渡，在环雾流流态下气芯夹带液滴从管子中部通过，并且带动液膜沿管壁上升，在环雾流初级阶段，更容易观察到液膜和液滴运移特征。

基于Grazia[16]、Mukherjee[12]以及牛朋[17]实验数据，得到段塞流—环雾流的流型转换界限方程为：

(6)

2.2.3 分层流

在倾斜管或者水平管中，由于重力分异，气体携带部分液滴在管道上部运移，水在管道下部形成液膜，这样的流态称之为分层流。

上倾管和下倾管分层流特征不同，使用Gra-zia[16]、Mukherjee[12]、Matsubara[18]以及牛朋[17]实验数据分别拟合得到上倾管和下倾管流型转换界限方程为：

上倾管：

(7)

下倾管：

(8)

2.3 各流型持液率计算方法

2.3.1 泡状流和段塞流

由于M-B模型在小气量和大水量条件下的误差较小，泡状流和段塞流采用M-B模型泡状流和段塞流的摩阻、压降计算方法[19]：

(9)

式中：Ngv—气相速度准数，无因次；NLv—液相速度准数，无因次。

式(9)中使用的速度准数为M-B速度准数，各个回归系数如表3所示。

表3 M-B模型回归系数表

在泡状流和段塞流中摩阻系数使用无滑脱摩阻系数fns：

(10)

式中：e—绝对粗糙度，m；Rens—无滑脱雷洛数，无量纲。

2.3.2 环雾流

环雾流流态下由于气体速度大于液体速度，两相摩阻系数考虑为相对持液率和无滑脱摩阻之间的函数。由于B-B模型在大气量条件下计算准确，可以使用B-B模型中的分散流摩阻和持液率计算模型[8]。

持液率为：

(11)

式中：C—倾管系数。

摩阻系数为：

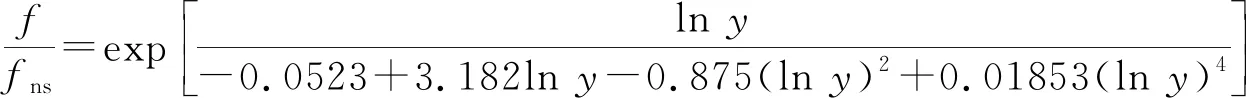
(12)

式中：f—滑脱摩阻系数;

fns—无滑脱摩阻系数。

2.3.3 分层流

对分层流，考虑液膜夹带的持液率计算方法为:

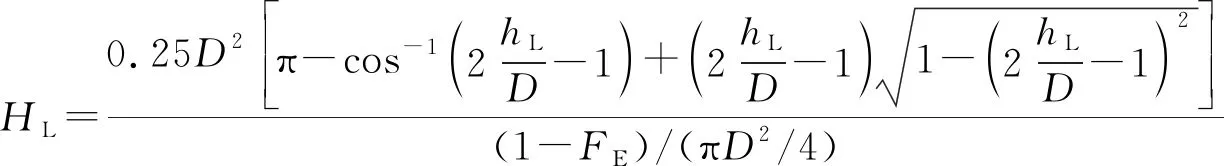
(13)

式中：FE—液膜夹带率；hL—液膜厚度，m。

分层流摩阻系数使用考虑滑脱的摩阻系数f。

3 应用效果评价

3.1 井筒压降实例计算

使用改进的页岩气水平井压降计算模型对实例井进行计算，计算结果如表2所示。本文提出的新模型通过优化流型转换界限和引入分层流持液率、摩阻系数计算方法的方式提升了压降计算的准确度。新模型在小水量大气量下的误差为4.03%，相比于M-B模型降低了43.00%，相比于B-B模型降低了6.05%；大水量下的误差为5.96%，相比于M-B模型降低了13.12%，相比于B-B模型降低了37.85%；平均相对误差为4.34%，相比于M-B模型降低了31.65%，相比于B-B模型降低了73.14%。

3.2 井筒流态分布特征

本文改进压降计算模型可对页岩气水平井井筒流态分布特征进行分析，以井N209H15- 2为例，使用本文模型计算了该井在产气量5×104m3/d，产水量14 m3/d的压力分布，与此时的流压测试数据对比，吻合度很高(见图1)。同时，使用本文模型计算得到了不同产气量,相同产水量条件下的井筒流态分布(见图2)。

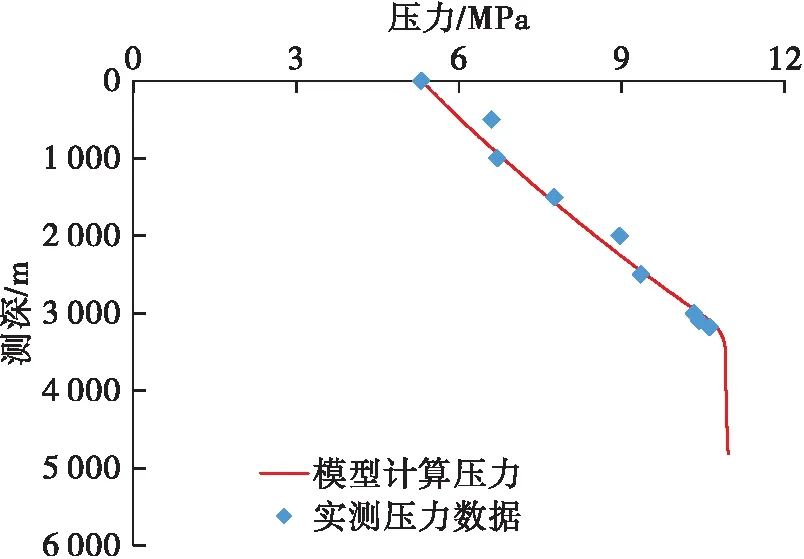
图1 实测压力与模型计算压力对比

M-B模型和B-B模型未考虑分层流无法得到包含分层流的井筒流态分布，也就无法对页岩气水平井井筒气水两相流动特征进行准确分析。使用本文模型计算得到，在产气量5×104m3/d、产水量14 m3/d时，垂深3 102.53 m以下井筒中为分层流，3 165.54 m以上为段塞流,见图2(a)。产水量不变，产气量增加到10×104m3/d后，井筒中3 102.53 m以下井筒中为分层流，3 102.53～1 902.3 m为段塞流，1 902.3 m以上为环雾流,见图2(b)。通常认为段塞流和泡状流是最不利于气井生产，为了预防气井井筒积液，下入速度管柱排水采气措施时，需要将小油管下入到段塞流以下才能最大限度改善气井流态，对于该井油管最佳下入深度为3 165.54 m。

图2 两种产量井筒流态分布

4 结论

本文基于对M-B模型和B-B模型的准确性分析，通过国内外大量实验数据优化了泡状流、段塞流和环雾流型转换界限，并引入分层流持液率和摩阻计算方法，建立了页岩气水平井生产压降计算新模型，使用现场数据对该模型进行验证，并对气井井筒流态分布进行了分析，得到的结论如下：

(1)通过现场实测数据计算对比，M-B模型对泡状流—段塞流的流型划分和摩阻、持液率描述准确，使得M-B模型更适用于小气量和大水量条件；B-B模型对段塞流—环雾流的流型划分和摩阻、持液率描述准确，使得B-B模型适用于大气量条件。

(2)对长宁区块多井对比分析表明：新模型在小水量大气量下的误差为4.03%，大水量下的误差为5.96%，平均相对误差为4.34%，新模型相比于常规模型具有更高的准确度和更广的适用范围。

(3)新模型可判断水平段分层流流态，为排水采气措施提供数据支撑。使用本文模型对N209H15- 2实例分析得到的流态分布表明，速度管柱最佳下入深度为测深3 165.54 m。