航空电机无位置传感器自抗扰控制技术研究

李 庚，米乾宝，顾 鹏，黄 俊

( 西安航天精密机电研究所，西安710100)

0 引 言

近年来，随着技术的发展，永磁同步电动机(PMSM)以其高可靠性、高功率密度、简单的构造和优越的性能，广泛应用在诸如航空航天、交通牵引、军事军工和工业机器人等领域[1-2]。同时无位置传感器控制技术的出现，也使得PMSM更适应航空电机恶劣的环境、极端的可靠性指标和变负载要求和宽速域的转速要求。

永磁同步电机无位置传感器控制技术可根据适用速域分为两种，在中高速域采用的是基于电机数学模型的控制技术，在低速域多采用基于电机凸极效应的高频注入法，如高频方波注入法。由于低速域电机反电势较低，不易检测电机转子位置信息，所以高频注入法是当今研究的关键和难点，而且由于电机系统模型不精确、外部周期性干扰和非周期线性干扰的存在、内部参数的变化都会降低无位置传感器控制系统的控制性能[3-4]。高频方波注入法在多种低速域无位置控制技术中，注入频率高，动态性能较好，但其受电机参数影响较大，鲁棒性较差。

针对上述问题，本文采用自抗扰控制技术配合高频方波注入的无传感器控制系统，为提高系统抗干扰能力和动态性能，对干扰进行估计和补偿，分别设计电流环、速度环的由扩张状态观测器和非线性控制律(NLSEF)组成的ADRC控制器，并采用冻结系数法提出了二阶非线性ESO的参数设定原则，具有一定的参考价值。为验证设计抗干扰性，在Simulink中搭建无位置传感器控制系统对控制系统进行了仿真验证。

1 自抗扰控制技术

在电机运行过程中，会受到周期性和非周期性的扰动，周期性扰动如齿槽转矩、死区效应、电机永磁体磁链谐波等，非周期性扰动如电机运行过程中电阻电感参数变化、负载转矩变化、工作条件变化等，会使电机的非线性加大，使控制性能下降[5]。

自抗扰控制(ADRC)中，将系统受到的总扰动扩张为系统的一个状态，使其可以被扩张状态观测器观测到并加以补偿，使系统成为理想的“积分器串联型”系统，从而获得理想的控制效果，这个过程就是自抗扰控制的“动态补偿线性化”[6]。

为实现扰动估计和动态补偿线性化，传统ADRC控制器由三部分组成，即微分跟踪器(TD)、扩张状态观测器(ESO)和非线性控制律。微分跟踪器用来安排“过渡过程”和产生微分信号，避免系统超调，但是会降低转速环电流环的动态性能，为简化系统设计，本文在设计中去除TD，控制器结构如图1所示，本设计的ADRC由非线性扩张状态观测器和非线性误差反馈控制律(NLSEF)组成。非线性函数fal(e,a,δ)函数是ADRC控制中的一个经典函数，是“大误差小增益，小误差大增益”的控制思想一种体现，非线性误差反馈控制律的效果好于线性控制律，所以采用非线性函数fal(e,a,δ)函数作为控制律和观测器的核心函数。扩张状态观测器(ESO)是ADRC控制器的重要组成部分，用以观测系统中的总扰动。非线性控制律中补偿总扰动，输出补偿后的控制量u(t)使系统成为理想的线性积分器串联型系统。

改进后的自抗扰控制器结构如图1所示，如式(1)、式(2)所示，ESO接受反馈信息，以z1跟踪转速ωr，以z2为ESO观测的扰动信息，由初始控制量u0(t)和观测值z2得到动态扰动补偿线性化后的控制量u(t)，以实现对扰动的估计和补偿。

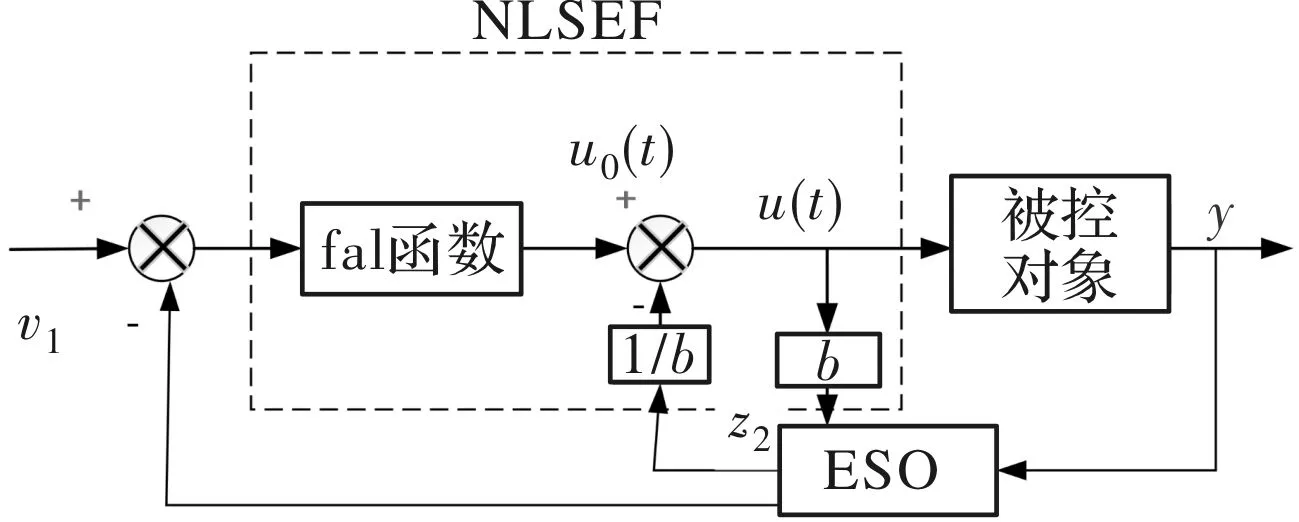
图1 自抗扰控制器原理图

非线性扩张状态观测器：

(1)

非线性误差反馈控制律：

(2)

式中，z1为对系统反馈y的状态估计;z2为对系统总扰动的估计;β01、β02分别为误差增益系数；v1为系统给定速度；u0(t)为初始输出信号；u(t)为控制器输出的补偿后的控制信号；b为控制参数；fal(e,a,δ)为最优控制函数。

(3)

式中，δ为函数线性区域的长度，α为增长因子，且0<α<1，一般取0.5。

2 转速环电流环自抗扰控制器设计

先进行转速环自抗扰控制器的设计，将外部干扰和内部干扰纳入到电机模型中，改写电机模型可得PMSM的转速环数学模型:

(4)

(5)

其中,Qω为总扰动f(ωr,TL)的微分，转速环成为二阶系统，针对系统(5)，设计转速环ADRC控制器如下：

扩张状态观测器：

(6)

非线性误差反馈控制律：

(7)

式中，z1为对反馈转速ωr的状态估计，z2为对系统扰动的观测值，控制参数bω=ψfp/J。

电流环的控制性能直接影响电机系统的控制性能，然而电流环也受到包括外部温度、负载变化造成的干扰、电机永磁体磁链谐波等干扰，电路中引入的IGBT或MOSFET死区造成的非线性因素和其他未建模因素等。我们将上述电流环受到的扰动代入到电流环方程中可得:

(8)

式中，γid、γiqγiq分别为电流环d、q轴未建模扰动。

(9)

(10)

式中，z1为d-q轴反馈电流idq的状态估计，z2为扰动信号的观测值；udq0为电机d-q轴的初始控制信号，udq为补偿输出信号。

相比于线性ADRC，采用非线性函数如fal(e,a,δ)函数等的非线性ADRC，控制效率更高、误差更小，但是非线性ADRC的参数整定一直是一个难题，只能凭借工程经验进行，没有明确的设计原则。本文采用“系数冻结法”，分析非线性ESO带宽及参数配置原则。以转速环二阶ESO为例，令F=fal(e,a,δ)/e，通过计算可知F是一单调函数，对转速环ESO冻结参数进行拉普拉斯变换可得

(11)

令bωiq=-f0，则有f0到z2(s)的传递函数

(12)

可知其幅相特性为

(13)

在频域内，我们可以类似线性系统，给出非线性ESO的频域指标，在给定的频域范围ω∈[0,ω0]的范围内，开环传递函数G(s)应满足:

(14)

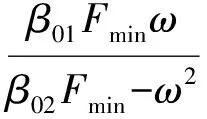
(15)

由幅频特性公式可见，随着F的增大，A(ω)减小，则容易得出要使观测器幅频特性满足|A(ω)-1|≤A0，则需要

(16)

依据以上分析并结合文献[7]，给出二阶非线性ESO符合频域指标的参数选择的原则，即充分条件：

(17)

3 控制系统仿真验证

以上述自抗扰理论设计转速环、电流环自抗扰控制器，搭建基于ADRC的高频方波注入无位置控制仿真系统，以式(17)配置转速环电流环控制器参数，分别验证控制系统在突加、突减负载、周期负载和变工况情况下的表现。自抗扰控制器原理图如图1所示，无位置传感器控制系统框图如图2所示。

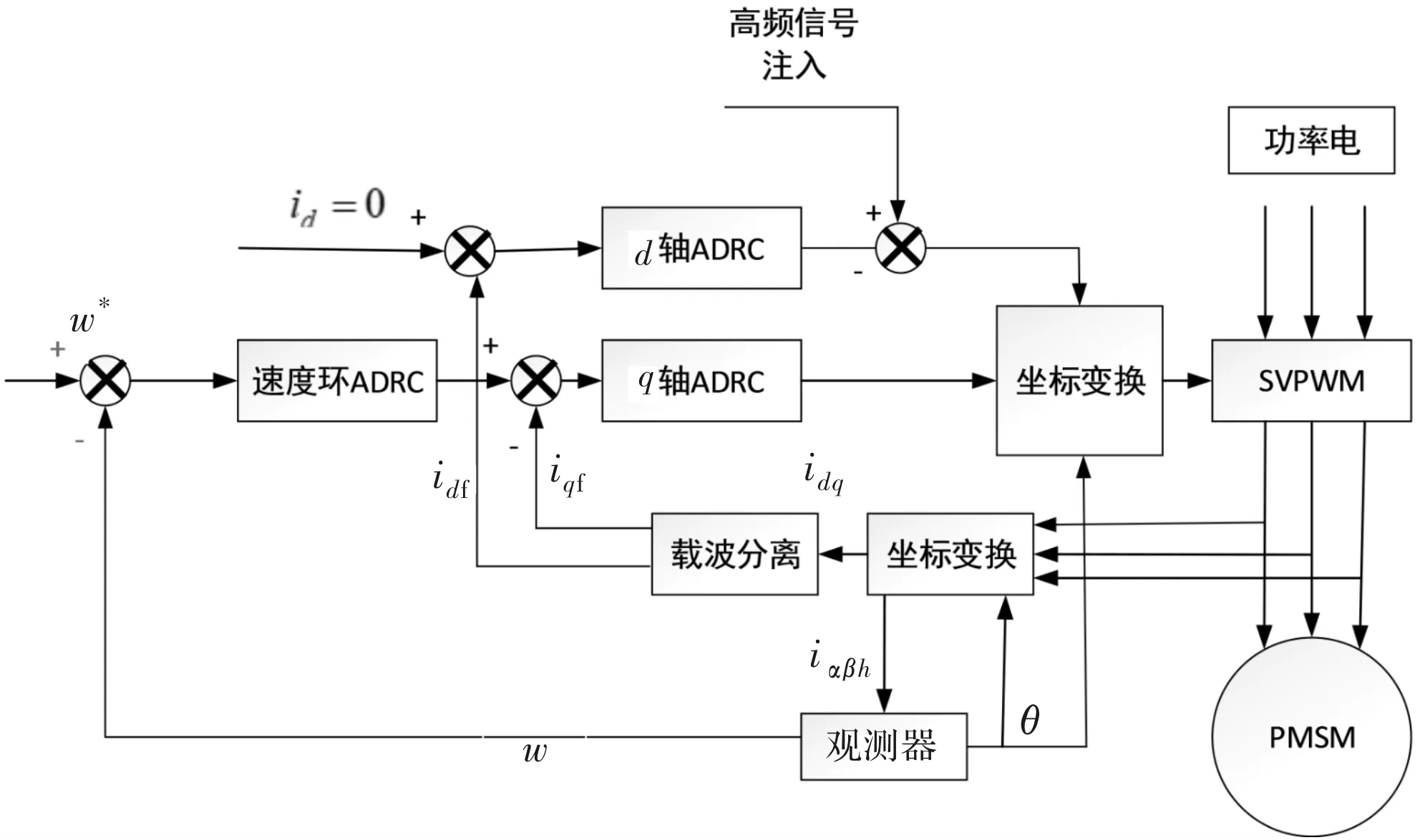
图2 ADRC无位置传感器控制原理图

本文的控制对象为凸极式永磁同步电机，其具体参数如表1所示。

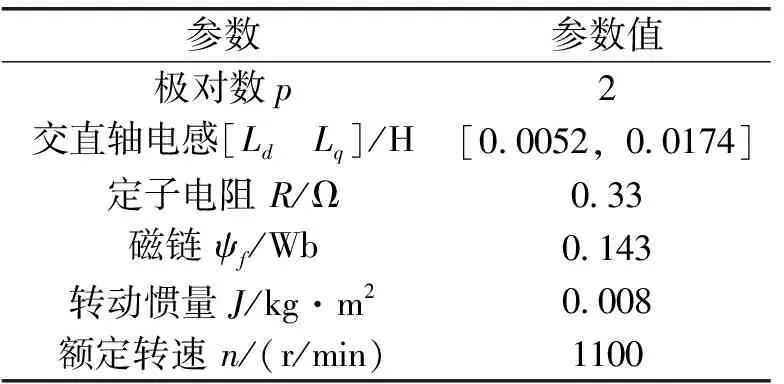
表1 永磁同步电机参数

为验证系统低速运行及抗外部干扰能力，进行加减负载实验，给定转速100 r/min，在0.2 s分别加载2 Nm、4 Nm、6 Nm的大负载力矩，在0.4 s消去2 Nm、4 Nm、6 Nm的负载力矩。图3即为ADRC控制系统的响应，其中图3(a)为转速响应曲线，图3(b)干扰力矩估计值。系统借助ESO估计出包含外加力矩在内的总干扰，在2 Nm、4 Nm、6 Nm的大负载力矩下转速降分别为0.6 r/min、2.2 r/min、5 r/min，并在0.002 s、0.004 s、0.01 s内经有限次振荡后回归稳定。

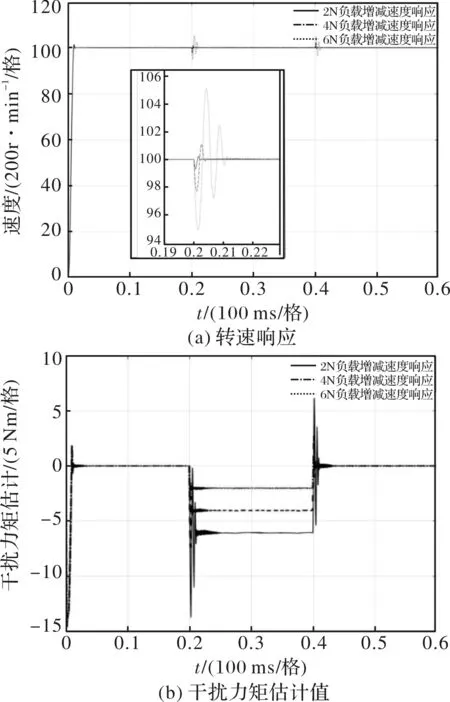
图3 电动机控制系统负载突变响应

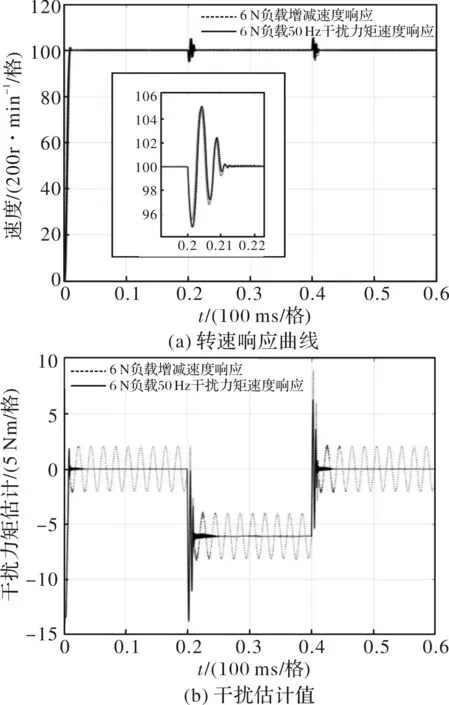
图4 周期干扰实验结果

以幅值2 Nm，频率50 Hz的周期力矩在6 Nm大负载突加突减实验中模拟周期干扰进行实验。图4为实验结果，其中图4(a)为转速曲线，图4(b)为外部扰动估计值曲线，系统估计的外部干扰幅值为2 Nm，频率50 Hz，调速转速降变化较大，可能是因为外加周期干扰与调速时电磁力矩形成了耦合。

周期干扰试验的系统响应如表2所示，系统受幅值2 Nm，频率为50 Hz的周期干扰负载时，输出转矩含有幅值为2 Nm，频率为50 Hz的周期性补偿力矩，结合图3、图4，系统对阶跃和周期性干扰力矩均有优秀的估计补偿能力。

表2 自抗扰控制系统实验数据

用多组电机内阻值模拟不同工作环境对电机参数造成的系统内扰，分别设定电子电阻R为5 Ω、3 Ω、1 Ω、 0.5 Ω、0.33 Ω 和0.11 Ω，设定额定转速100 r/min起动，在0.2 s使转速降至0，在0.4 s再提升转速至100 r/min，转速响应如图5所示，在1 Ω以下的定子阻值下系统超调为1.5%，在3 Ω阻值时系统超调为1.3%，在定子阻值为5 Ω时系统超调为1.8%，超调均在5%以内，调整时间ts分布在8 ms～11 ms区间，可见在电机参数失配时，自抗扰控制系统仍有良好的动态响应：从不同干扰条件下系统调速仿真结果可知，系统的性能优良，能够估计补偿不确定的内部和外部干扰，系统对复杂工况引起的电机系统内部参数变化不敏感，对于航空电机应用在复杂极端、没有精确理想模型的航空电机工作领域极其重要，使自抗扰控制具有更强的工程价值。

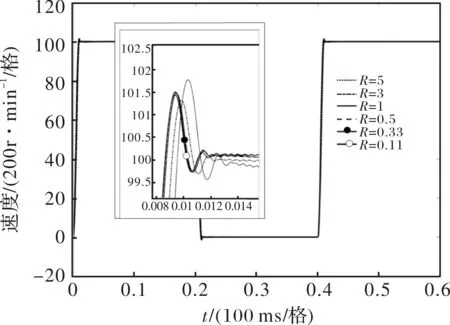
图5 不同参数的转速响应

4 结 语

为了设计具有更强抗干扰能力的低速无位置传感器控制系统，本文选择将自抗扰控制技术增强高频方波注入法，其特点是，将系统内外扰动统一扩张为系统总扰动加以补偿，系统抗扰能力强，且对被控电机参数不敏感，可以有效增强高频方波注入法的鲁棒性。采用“冻结参数法”分析ESO并给出了参数调整原则，简化了非线性ESO参数的调整。并进行了Simulink 仿真，搭建基于ADRC算法的改进型高频方波注入模型，结果表明结合ADRC控制器的改进型高频方波注入法响应快速、超调小，对工况变化和外部干扰有极强的适应能力，负载突变时和转速指令突变时均有优秀的转速响应，能够准确估计干扰并加以补偿，进一步提高了高频注入技术在航空领域的适应性和鲁棒性。