单分子瞬时带电态中电子-振动耦合特性的亚纳米荧光成像研究*

田晓俊 孔繁芳 经士浩 郁云杰 张尧 张杨2)† 董振超2)‡

1) (中国科学技术大学合肥微尺度物质科学国家研究中心,合肥 230026)

2) (中国科学技术大学物理学院,合肥 230026)

1 引言

分子体系中的电子-振动耦合效应是指分子中的电子运动和核运动之间的相互作用.该效应对分子光谱以及能量转移等特性有重要的影响,是分子光谱学研究中的核心问题之一[1-9].由于电子的质量比原子核小得多,因此核外电子的运动速率比起核运动要快得多,一般认为,当核发生微小位移时,电子会立即调整其位置从而适应新的势场,而原子核则对电子的瞬时变化不太敏感.玻恩-奥本海默近似正是基于这样的物理图像提出来的,它允许将原子核坐标与电子坐标近似地进行变量分离,从而将求解整个体系波函数的复杂过程分解为分别求解电子波函数和原子核波函数的两个相对简单的过程[5].在此近似框架下,当分子发生能态间的电子跃迁时,根据弗兰克-康登(Franck-Condon,FC)原理,分子原子核构型被认为是静止的,即发生了垂直跃迁现象,吸收或发射光子的强度正比于电子基态和电子激发态中振动波函数重叠积分的平方[1].然而,在实际的电子跃迁过程中,分子原子核的动态运动(即分子振动)会改变电子基态和电子激发态的波函数分布,从而引起原本FC 原理所禁阻的跃迁过程的发生[1,6,7].因此,要系统深入地理解分子中的电子-振动耦合效应,就需要超越基于FC原理的传统图像描述,考虑分子振动对电子态波函数的影响,即考虑Herzberg-Teller (HT)项的贡献[4,8].可是,由于HT 项的贡献一般较小,而且传统远场光学表征技术受到衍射极限的制约,难以在单分子尺度上研究分子的电子-振动耦合的微观特征,因此,如何从实空间研究电子-振动耦合的微观物理图像,搞清楚分子振动具体是如何影响电子跃迁过程的,一直是个挑战,而且这种挑战对于瞬态充电分子而言尤为严峻,因为还涉及如何产生瞬时充电态的问题.

扫描隧道显微镜诱导发光(scanning tunneling microscope induced luminescence,STML)技术利用隧穿电子激发的高度局域特性以及纳腔等离激元的局域增强效应,突破了传统远场光学表征技术中衍射极限的制约,实现了具有亚纳米分辨的分子荧光光谱成像[10-18].此外,STML 技术还可以展示分子丰富的振动分辨的光谱特征[10-13,16,18-21].2021 年,Kong 等[22]利用STML 技术研究了单个并五苯分子内的电子-振动耦合特性,从实空间的角度,揭示了单个中性并五苯分子内具有不同对称性的振动模式对电子跃迁的影响.与中性分子相比,分子的瞬时带电态对应着分子的氧化或还原状态,深入分析分子体系在带电状态下的电子-振动耦合特性对理解分子振动是如何影响化学反应中间过程等具有重要意义[23-25].此外,相对于中性分子,当分子处在瞬时带电态时,其光学带隙、跃迁偶极、电荷转移特性等光电行为都会发生显著的变化[16,26-28].STML 技术具有对分子进行局域电子充电激发和亚纳米分辨荧光成像的功能,为揭示分子在瞬时带电状态下的光电行为和电子-振动耦合特性提供了可能性.

本文以具有丰富的光电特性的苝四甲酸二酐(perylene-3,4,9,10-tetracarboxylic acid dianhydride,PTCDA)分子为研究对象,不仅因为其可被充电[17,26,29],而且还因该分子呈简单的直线型结构(D2h对称性),结果便于分析比较.首先,我们将PTCDA分子分散沉积在银衬底支撑的氯化钠薄层表面上.根据文献[17,26,29] 的报道,吸附于该表面上的PTCDA 分子会被充电,呈—1 价.随后,我们利用STML 技术,通过调控激发偏压的极性和大小,改变了PTCDA分子的价态,研究了分子的瞬时带电态(—2 价态)的电致发光特性以及相应的电子-振动峰的实空间成像特征.将光谱成像与理论计算相结合,从实空间揭示了在当分子在瞬时的—2 价态下,分子振动对电子跃迁的影响,并对电子-振动耦合的微观图像进行了深入分析.

2 实验体系和理论模型

2.1 实验体系

本文所有STM 图像和STML 测量都是在低温(约7 K)超高真空(约1×10—10Torr,1 Torr=133.322 Pa)的STM(Unisoku)与高灵敏度的光学探测相结合的联用系统中完成.我们通过多轮的氩离子溅射和高温退火获得干净平整的Ag(100)衬底表面,利用电化学刻蚀的方法获得Ag 探针,并在超高真空环境中对探针尖端进行氩离子溅射和电子束轰击处理,随后,还在干净的Ag(100)表面对探针尖端通过下扎与打脉冲等方式进行进一步修饰,以获得所需的纳腔等离激元(nano-cavity plasmon,NCP)共振模式.我们通过热蒸发的方法在Ag(100)表面沉积了部分覆盖的4 层氯化钠(NaCl)岛(4ML-NaCl/Ag(100)),并通过原位热蒸发的方法将PTCDA 分子沉积到衬底表面,以获得孤立分散的分子样品.根据文献[17,26,29]报道,由于PTCDA 的电子亲合能高于NaCl/Ag(111)衬底的功函数,因此,当PTCDA 分子吸附在NaCl/Ag(111)衬底上时,其带有一个负电荷.本文STM 图像和光谱测量都是在所标注偏压下以恒流模式进行采集,相关的光路图与光谱仪等设备可以参见前期工作中的相关描述[14,30].微分电导谱(dI/dV)是通过锁相技术测量的,所采用的调制偏压为20 mV,所采用的调制频率为329 Hz.

2.2 理论模型

本文对PTCDA 分子振动模式、电荷分布、跃迁偶极等的计算均基于密度泛函理论(density functional theory,DFT)的Gaussian16 软件包来完成的.计算选择的泛函为B3LYP 混合泛函,基组为6-31G(d).首先对分子结构进行优化,然后在优化结构的基础上进一步计算分子的振动频率、激发态和振动荧光光谱.对分子跃迁电荷密度、跃迁偶极和原子电荷等的分析都是基于自主编写的Matlab程序包来实现的.

3 结果和讨论

单分子的荧光光谱常包含丰富的电子-振动峰[2,10,12,21,31-33],是研究分子内电子-振动耦合特性的一种重要方法.本文也正是利用单个PTCDA分子瞬时带电态的电致荧光光谱来研究相关的电子-振动耦合特性.我们利用高度局域化的隧穿电子来激发孤立的单个PTCDA 分子,在较高的正偏压条件下,隧穿电子被注入分子,使得分子被激发到瞬时充电态(—2 价)的激发态上.如图1(a)所示,为获得STM 隧道结中单个PTCDA 分子瞬时带电态的荧光光谱,我们首先通过制备4 层NaCl岛作为介电脱耦合层将分子和Ag(100)衬底分开,从而有效抑制了金属衬底所导致的荧光淬灭;其次,还通过可控地修饰Ag 探针尖端形貌,获得很强的NCP增强效应,从而产生了较强的分子电致荧光,保障了STML 光谱以及能量分辨的光谱成像具有足够的信噪比.图1(b)展示了在1 V 偏压下,4ML-NaCl/Ag(100)表面上孤立的单个PTCDA分子的STM 图像.PTCDA 分子均呈现出了两个瓣的形貌特征.由于单个PTCDA 分子呈—1 价,因此分子的最低未占据分子轨道(lowest unoccupied molecular orbital,LUMO)呈半占据状态,在没有扰动情况下该半占据态处于费米能级的位置.在后续讨论中,为了保持对不同带电态分子轨道的指认一致性,本文均使用中性分子的HOMO,LUMO或者LUMO+1 等轨道来讨论.然而在STM 测量过程中,在正、负偏压的作用下会伴随着电子的注入和抽取,而不同的库仑排斥相互作用会导致这个半占据LUMO 态劈裂成能量高于和低于费米面的两个Hubbard 态,从而在正、负偏压下都形成共振隧穿通道[17,29].dI/dV实验结果也与这些物理图像相吻合.如图1(d)所示,在正负偏压下,我们分别观察到了单电子未占据分子轨道(singly unoccupied molecular orbital,SUMO)和单电子占据分子轨道(singly occupied molecular orbital,SOMO)[17,29].这一实验观察也再次佐证了吸附在4 ML-NaCl/Ag(100)表面上的PTCDA 分子在基态时带有一个负电荷.当探针位于分子长轴的位置(如图1(b)中红色“×”所示)并在+3 V 偏压下激发分子时,分子电致发光谱表现出尖锐的多峰特征,如图1(c)中的红色曲线所示.光谱最高能量的发光峰的峰位在约662 nm 处,这很可能对应于—2 价PTCDA 分子的纯电子跃迁发射峰(即0-0 跃迁峰);此外,在能量较低位置存在许多尖锐的发光峰,这些发光峰很可能对应于—2 价PTCDA分子荧光的电子-振动峰.为了更好地分析这些电子-振动峰,我们先以分子0-0 跃迁峰位作为能量偏移的零点,得到了STML 光谱中更低能量的振动峰相对于0-0 峰的能量偏移[20,21];然后,再利用DFT 理论计算出了具有振动分辨的单个—2 价PT CDA 的荧光光谱(图1(c)的绿色曲线),随后,将其与实验获得的红色曲线相对比,发现它们之间有很好的对应关系.这种一致性不仅证实了我们对662 nm 处的0-0 峰归属的正确性,而且也可以更好地关联不同振动峰与所属的振动模式及其对称性等信息,同时也再次印证了荧光发射的确是源自—2 价的PTCDA 分子.

图1 具有振动分辨的单个PTCDA 分子瞬时—2 价的电致发光 (a)利用STML 技术研究PTCDA 分子电致荧光的实验示意图;(b)吸附在4 ML-NaCl/Ag(100)表面PTCDA 分子的STM 扫描图像,扫描条件为1 V,2 pA;插图为单个PTCDA 分子的STM 扫描图像与对应取向的分子结构示意图;比例尺为3 nm;(c)红色曲线对应在图(b)中红色“×”处激发时获得的STML 光谱(+3 V,50 pA,60 s),绿色曲线为DFT 理论计算的单个—2 价PTCDA 分子的荧光光谱;(d)黑色曲线对应在图(b)中红色“×”处测量的dI/dV 谱(—3 V,40 pA),蓝色点线为不同偏压下分子STML 发光强度统计;(e)瞬时—2 价PTCDA 分子的STML 发光机制示意图Fig.1.Vibronically resolved electroluminescence from a single transient doubly charged PTCDA molecule.(a) Schematic of the STML experiment on a single PTCDA molecule on 4 ML-NaCl/Ag(100).(b) STM image of isolated PTCDA molecules adsorbed on 4 ML-NaCl/Ag(100) (+1 V,2 pA),with the molecular structure given in the inset showing molecular orientation corresponding to the inset STM image.(c) Typical STML spectrum (+3 V,50 pA,60 s) (red curve) acquired at the red “×” marked in (b).A DFT simulated fluorescence spectrum from a single doubly charged PTCDA molecule is also plotted for comparison (green curve).(d) Typical dI/dV spectrum (black curve) acquired at the red “×” marked in (b).The setpoint for the dI/dV measurement was—3 V and 40 pA.The molecular emission intensities at different excitation voltages are also shown (blue filled rectangles).(e) Schematic of the mechanism for the molecular electroluminescence of PTCDA2—.

此外,结合偏压依赖的发光强度以及dI/dV谱的测量,我们还研究了瞬时—2 价PTCDA 分子的发光机制.从图1(d)的dI/dV谱上可以看出,分子LUMO+1 轨道的起峰偏压为+2.4 V,而+2.4 V 也正是可以探测到—2 价PTCDA 分子的电致发光信号的阈值偏压(图1(d)的蓝色曲线),这表明分子电致发光的实现与电子注入分子LUMO+1 轨道密切相关.这样一来,结合注入发光机理[34],具体的—2 价PTCDA 分子的电致发光微观机制可以分为以下3 个步骤(见图1(e)):1)当分子LU+1 能级(实际上是近似简并的LUMO+1 与LUMO+2 轨道的混合能级[29])低于针尖费米面时,针尖电子注入分子LU+1 轨道,形成—2 价PTCDA 的瞬时激发态;2)该电子通过辐射跃迁至分子SUMO 轨道,值得指出的是,该辐射跃迁速率会被纳腔等离激元大幅增强;3)处在“SUMO”轨道的一个电子通过隧穿进入衬底,整个PTCDA 分子再次回到—1 价态.

纳腔等离激元不仅对加快辐射衰减速率至关重要,而且也在将隧道结中分子的发光信号耦合到远场的过程中起关键作用.通过研究单分子内位置依赖的STML 点谱,可以获得等离激元-激子耦合的方向依赖关系[19,21,35],进而揭示每个电子-振动峰所对应的跃迁偶极取向,加深对分子振动是如何影响电子跃迁过程的理解.图2(a)为在PTCDA分子的3 个典型位置上获得的代表性的STML 点谱.从谱线的特征上看,在不同位置激发时,不同电子-振动峰的发光能量基本相同,而相对强度却发生了较大变化.具体而言,当探针位置沿着分子短轴方向激发时(如图2(a)插图的蓝色“×”位置所示),v1振动模式(发光峰位约673 nm,对应的振动能量约248 cm—1)表现出很强的发光强度;而在长轴方向激发时(如图2(a)插图的红色“×”位置所示),v1振动模式发光强度却变得很弱.v1振动模式发光强度的位置依赖特征与0-0 跃迁峰的位置依赖关系一致,同时变强或变弱.与此不同的是,对于v2振动模式(发光峰位约707 nm,对应的振动模式约978 cm—1),该模式在长轴方向激发时表现出较强的发射峰,而在短轴方向激发时却几乎看不到信号.当在分子中心激发时(如图2(a)插图的黑色“×”位置所示),由于此时由分子与探针形成的系统净偶极大小受整体对称性影响而几乎变为零,因而所有的发光峰都变得很弱[14,19].值得一提的是,v1振动模式发光强度的位置依赖特征与0-0跃迁峰的位置依赖关系一致,而v2振动模式的位置依赖特征却与0-0 跃迁峰的位置依赖关系不同.这暗示了v2振动模式对电子跃迁过程具有明显的扰动.

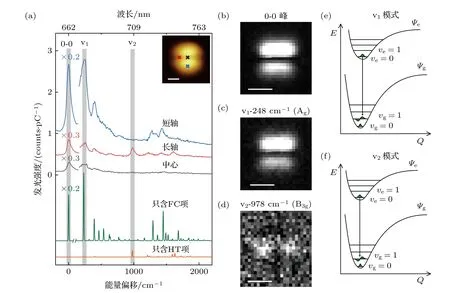
图2 位置依赖的STML 光谱和特定振动峰的光谱成像 (a)上面3 条曲线分别为激发分子不同位置获得的STML 光谱(+3 V,20 pA,60 s),下面2 条曲线分别为理论计算的FC 项(绿色)和HT 项(橘色)单独贡献的光谱;(b)—(d)分别为0-0 峰、v1 模式和v2 模式能量分辨的实空间光谱成像(+3.5 V,30 pA,每像素点3 s),每条光谱均已扣除等离激元背景;(a)—(d)比例尺均为1 nm;(e),(f)基于DFT 理论计算的v1 模式和v2 模式的势能曲线示意图Fig.2.Position-dependent STML spectra and spectroscopic imaging for selected vibronic peaks.(a) Three typical STML spectra(+3 V,20 pA,60 s) acquired at the positions marked in inset.Also plotted are calculated spectra for the contributions from either FC term (green curve) or HT term (orange curve) alone.(b)—(d) Energy-resolved spectroscopic images for the 0-0 peak (b),the v1 mode (c),and the v2 mode (d).Imaging condition:+3.5 V,30 pA;3 s per pixel.The NCP spectral backgrounds in spectroscopic images are subtracted.Scale bars in (a)—(d) are 1 nm.(e),(f) Schematics of the potential energy curves for the v1 mode (e) and the v2 mode (f) based on the DFT calculations.

为了更加直观地分析分子振动对跃迁偶极取向的影响,在扫描单个PTCDA 分子的同时,每个扫描点都采集了一条光谱,获得了瞬时—2 价PTC DA 分子的光谱成像图[14,20],从而获得了不同电子-振动峰空间分布的全景图.如图2(b)—(d)所示,0-0 峰、v1峰和v2峰的成像特征都呈现出“两点”亮斑特征,但v2峰的“两点”亮斑取向发生了变化.对于0-0 峰和v1峰,“两点”亮斑的方向沿着短轴方向(亮斑上下不对称是由于针尖尖端形貌的不对称所引起的),表明沿着短轴方向激发时发光更强;而对于v2峰而言,与0-0 峰相比“两点”亮斑的方向旋转了90°,变成了沿长轴方向.根据文献[14,19],“两点”亮斑的方向可以直接反映分子跃迁偶极的取向,因此,可以得出0-0 纯电子跃迁和v1振动峰的跃迁偶极取向均沿着分子短轴,而v2振动峰的跃迁偶极却沿着分子长轴.也就是说,v2振动模式对纯电子跃迁过程产生了强烈的扰动,这也意味着发生了很强的电子-振动耦合作用.值得一提的是,只有沿着NCP 径向极化场方向的跃迁偶极发射才能被有效增强[19,21,35],因此,跃迁偶极沿短轴(长轴)方向的v1(v2)模式仅在沿短轴(长轴)方向激发时,才可以被有效增强.这种NCP 近场对跃迁偶极取向的选择性局域增强,对于清晰观察HT 贡献占主导的电子-振动峰信号至关重要.因为这类HT 贡献占主导的电子-振动峰信号常常很弱,在传统远场光学实验中很难被探测到[31,36].

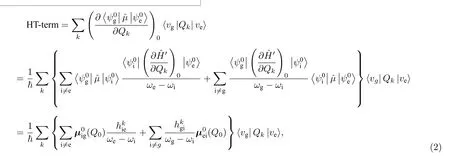
电子-振动耦合本质上是一个电子和振动自由度相互纠缠的量子过程.但在实际分子光谱的计算中,常常采用半经典的方法,在玻恩-奥本海默近似的框架下将电子和核坐标分开来处理.在这种情况下,可将分子振动视为微扰项[2,20,37,38],那么,不同电子-振动峰所对应的电子跃迁偶极可以表示为

其中ve(vg)代表激发态(基态)的核振动波函数,µeg(Q0)代表在平衡构型Q0下分子的静态跃迁偶极,Qk代表分子第k个振动的简正坐标.

在(1)式中,第1 项代表FC 项,描述了在静态核构型下的垂直电子跃迁,在涉及全对称振动的偶极允许的电子-振动跃迁中起主导作用.FC 项源自于与0-0 纯电子跃迁(µeg(Q0))相同的电子态,其大小正比于振动波函数的重叠积分(即FC 因子).根据选择定则[2,18],只有当电子跃迁的克罗内克积Γe⊗Γd⊗Γg包含全对称表示时,对应的电子跃迁才是偶极允许的,这里Γg,Γe和Γd分别代表电子基态、激发态和偶极算符的不可约表示.(1)式的第2 项代表HT 耦合项.在这一项的贡献中,显然还需要考虑分子振动的对称性Γv,即只有当克罗内克积Γe⊗Γd⊗Γg⊗Γv包含全对称表示时,HT 项才会发挥作用.HT 耦合项描述了分子振动对电子跃迁的动态影响,对其存在本身的认识就已经超越了基于常规FC 原理的理解图像.

基于上述理论框架,在图2(b)和图2(c)中,v1模式与0-0 峰表现出相同的跃迁偶极取向,这意味着FC 项贡献对v1峰发光起主导作用.有意思的是,与0-0 峰相比,v2峰的跃迁偶极取向发生了显著变化,这表明HT 项贡献对v2峰发光起主导作用.换句话说,从实验获得的光谱成像图中所反映的不同电子-振动峰跃迁偶极取向与0-0 纯电子跃迁偶极取向之间的关系,就可以判断电子-振动耦合中的主导贡献是什么,是FC 主导,还是HT 主导.

值得一提的是,这种对电子-振动跃迁的主导贡献的指认也与DFT 理论计算结果一致.图2(a)中绿色和橘色曲线分别表示理论计算获得的只含FC 项和HT 项贡献的发光光谱.通过对比理论计算曲线与实验数据,研究发现,v1峰的确由FC 项贡献所主导,而v2峰则主要是HT 项贡献所主导.这些DFT 计算结果也对理解在电子振动跃迁中平衡核构型的改变提供了重要信息,如图2(e)和图2(f)所示.具体而言,v1电子-振动峰对应的跃迁中电子激发态和基态的势能曲线极小值之间有明显的位移,那么,根据FC 原理,这将产生很大的FC 项贡献.然而,在v2电子-振动峰所对应的跃迁中,势能曲线则几乎没有偏移,这意味着相应的FC 项贡献是可以忽略的(因为FC 因子基于振动波函数对称性原因几乎为零),因此我们所观察到的v2峰应该主要源自HT 项的贡献,即反映出了v2分子振动对电子跃迁过程的强烈动态扰动.

由于在电子跃迁的过程中,电荷密度会在分子上重新分布,因此,分子原子核会通过振动来对新的库仑力场做出响应,从而在发射光谱上产生电子-振动峰[1].为了在实空间更深入而直观地理解电子跃迁和分子振动之间的耦合,我们还对—2 价PTCDA分子跃迁密度以及由分子振动所诱导出的跃迁电荷的空间分布进行了DFT 理论计算.其目的是期望通过实验与理论结果的对比,回答什么样的分子振动会对电子跃迁产生强烈的扰动,同时,它们又是如何影响电子跃迁的?

为了回答上述问题,我们首先根据参与电子跃迁的轨道计算了纯电子跃迁偶极的空间分布,如图3(a)所示.可以看到0-0 纯电子跃迁所对应的跃迁密度振荡方向是沿着分子短轴方向的,这导致了理论模拟光子图中的沿着分子短轴方向的“两点”亮斑特征(图3(b))[39],同时也与实验结果一致.另外,图3(a),(c)和(f)的跃迁密度反映了电子跃迁概率的空间分布.可以看出在分子上下两侧的碳与氧原子具有较大的跃迁密度,因此,对这些原子具有较强扰动的分子振动模式就有可能引起较强的电子-振动耦合作用.

如图3(c)所示,对于全对称Ag的v1振动模式,分子振动特征主要体现在左右两端的碳和氧原子以全对称的方式膨胀和收缩,不会破坏分子固有的对称性.这种全对称的振动产生很强的FC 项贡献,与0-0 跃迁具有相同的对称性.值得指出的是,从对称性角度来分析,这种全对称分子振动对HT项也会有贡献.图3(d)展示的是通过DFT 理论计算的v1振动所产生的HT 项贡献的空间特征,全对称振动所诱导的跃迁电荷也是沿着短轴方向振荡,因此,也会导致沿着短轴方向的“两点”亮斑特征(如图3(e)所示).但需要强调的是,v1振动所诱导的HT 项贡献相较于FC 项贡献要小好几个数量级,可以忽略.因此,实验上观测到的v1模式的光子图的主要贡献仍然是源自于FC 项.

相比之下,如图3(f)所示,具有B3g反对称振动特性的v2模式,分子振动特征主要体现在左右两端的碳和氧原子以相反的相位发生面内形变振动.这样的振动特征会破坏分子原有的对称性,从而会诱导出很强的电子-振动耦合作用.对于v2振动,一方面,偶极允许的FC 项贡献仍然是沿着短轴方向,但由于平衡核构型几乎没有偏移(图2(f)),这导致了v2振动的FC 因子很小,FC 项贡献可以忽略.另一方面,由于HT 项贡献的存在意味着克罗内克积Γe⊗Γd⊗Γg⊗Γv必须包含全对称表示.在这种情况下(参考图4(a)的坐标系),只有沿分子长轴(y)方向的电子跃迁偶极分量才能保证该克罗内克积B1u⊗B2u⊗Ag⊗B3g=Ag.也就是说,B3g反对称的v2振动诱导出了原先沿长轴方向偶极禁阻的的电子跃迁(包含B3g不可约表示,而非全对称Ag表示).如图3(g)所示,v2振动的确对电子跃迁产生了强烈扰动,诱导出了大量的沿着长轴方向振荡的跃迁电荷.当针尖位于长轴方向时,该方向的电子-振动跃迁的辐射速率就会被NCP 极大地增强.相应地,理论模拟的光子图“两点”亮斑特征也是沿着长轴方向(图3(h)),这与实验上所观测到v2模式沿着长轴的“两点”亮斑特征(图2(d))一致.因此,结合理论与实验结果,与纯电子0-0 跃迁相比,v2电子-振动峰截然不同的光子图取向特征直接反映出了其振动诱导发射的本质.

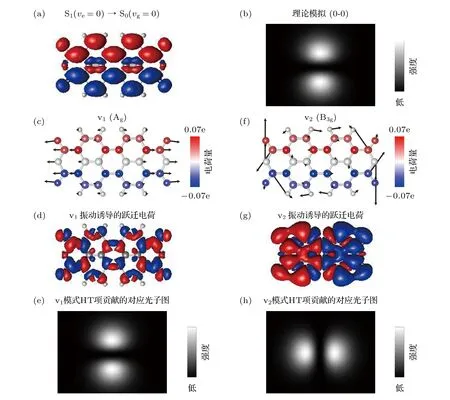
图3 跃迁密度和振动诱导跃迁电荷的模拟 (a)模拟的S1→S0 跃迁密度,其中蓝色和红色分别代表正、负电荷的空间分布;(b)理论模拟的0-0 跃迁的光子图;(c),(f)叠加了S1→S0 跃迁原子电荷分布的v1 和v2 振动模式示意图;(d),(g)计算的v1 和v2 模式振动诱导的跃迁电荷分布图;(e),(h)理论模拟的v1 和v2 模式HT 项贡献的光子图Fig.3.Simulations on transition densities and vibration-induced transition charges.(a) Simulated transition densities for the S1→S0 transition,where the blue and red colors indicate the spatial distributions of the positive and negative charges.(b) Simulated photon image for the 0-0 transition.(c),(f) Schematics of the vibrations for the v1 and v2 modes,superimposed with the S1→S0 transition densities distributed over each atom by Hirschfield population analysis.(d),(g) Calculated vibration-induced transition charges for the v1 and v2 modes.(e),(h) Simulated photon images of the HT-term contributions for the v1 and v2 modes.

图4 理论模拟的跃迁偶极矩和跃迁密度分布 (a)左图为PTCDA 分子结构示意图,为方便与不同跃迁的跃迁密度进行比较,右图再次展示了理论计算的—2 价态的PTCDA 分子的v2 模式振动诱导的跃迁电荷分布图;(b),(c)理论计算的沿着x,y 和z 方向的不同电子态间的跃迁偶极大小以及对应能量差;(d)理论模拟的不同电子态间跃迁的跃迁密度图Fig.4.Simulated transition dipole moments and transition densities.(a) Left:molecular structure of a PTCDA.Right:calculated vibration-induced transition charges for the v2 mode,which is shown again to facilitate the comparison with other transition densities between different electronic states given in the figure.(b),(c) Calculated values of the transition dipoles between different electronic states along x,y and z directions and the corresponding energy differences.(d) Simulated different transition densities between different electronic states.

研究者常常采用强度借用(intensity borrowing)模型来讨论这种振动诱导发射现象.该模型是一种更加严格的量子化表述,它认为振动诱导发射是通过与更高能量的电子态的混合来实现的[18,20,40].根据文献[22,40],HT 项贡献进一步展开为

这里也可以利用这种强度借用模型来理解v2电子-振动峰的产生以及该振动对分子波函数的扰动作用.在图4(a)坐标系下计算了不同电子态间的跃迁密度以及对应的跃迁偶极矩.从图4(b)和图4(c)可知,相邻电子跃迁S2→S0和S1→S4具有沿着长轴方向的非零跃迁偶极.再考虑不同电子跃迁之间的能量差,可以判断,v2振动诱导的辐射最有可能是从S2→S0的跃迁中借用了贡献.另一方面,也可从图4(d)中S2→S0的跃迁密度与v2振动诱导的跃迁电荷(图4(a)右图)空间分布的相似性得到类似的信息.形象地说,具有B3g对称性的v2振动很可能是使S1激发态的零阶电子波函数发生了较大畸变,将其“整形”成了类似S2态的分布形状,或者说使S1态和S2态之间发生了有效的混合,从而使v2振动诱导的辐射看起来好像是从S2→S0的跃迁中获得了较大的“借来”的贡献.值得一提的是,在同样具有D2h对称性的中性并五苯分子的电子-振动耦合研究中,具有B3g对称性的分子振动诱导辐射主要是从S1→S2跃迁中获得了较大的“借来”的贡献[22],B3g反对称性的分子振动主要是对基态电子波函数进行扰动.这样的差异很可能与—2 价态PTCDA 分子的S2等高能级电子态具有与中性并五苯分子的高能级激发态不同的对称性有关.

4 结论

本文利用NCP 局域增强特性,通过亚纳米分辨的电致荧光光谱成像,在实空间研究了单个PTCDA 分子瞬时带电态(—2 价态)的电子-振动耦合现象.研究发现,对于v1电子-振动峰,光子图的“两点”亮斑特征取向与0-0 峰相同,都是沿着分子短轴方向,其强度主要是FC 项贡献主导;对于v2电子-振动峰,其光子图的“两点”亮斑特征取向却沿着长轴方向,与0-0 峰相比旋转了90°.这反映了v2振动所引起的分子跃迁偶极取向的改变,意味着这时发生了很强电子-振动耦合,发光以HT项贡献为主,对其微观物理机制的描述必须超越传统的FC 图像讨论的范畴.结合理论计算,我们发现,对于反对称的分子振动,尤其是那些对具有较大跃迁密度分布的原子影响较大的分子振动,会强烈地扰动电子跃迁过程,并诱导产生大量振荡方向与纯电子跃迁偶极取向不同的跃迁电荷,引起振动诱导发光的产生.最后,我们还从强度借用模型的角度讨论了反对称振动对分子波函数的扰动及其所引起的振动诱导发光.本文结果为从实空间的视角来直观理解分子瞬时带电态中的电子-振动耦合的微观图像提供了新的途径.