基于多层K-means在森林点云中的单木识别算法

谷志新,裴方睿

(东北林业大学 信息与计算机工程学院,哈尔滨150040)

森林是世界上最重要的生态环境之一,对改善全球气候及生态环境起着重要的作用[1-2],而森林结构参数的准确测算对于林业资源的保护、精细管理与研究有着重要的意义[3-6]。森林结构的测算可以依靠彩色图像数据[7]或激光雷达[8]采集的点云数据,相对于彩色图像,点云数据可以更好地描述物体的几何信息。

激光雷达以激光束照射目标,物体表面将收到的激光束返射回传感器,通过回波脉冲和发射激光束之间的延迟得到采样点与传感器之间的距离,继而可以实现对森林结构参数的估测[9-13]。单木识别是估测单木结构参数的前提,现在已有多种算法能够成功提取森林点云中的单木。根据点云数据处理方式的不同,可将已有的单木识别算法分为二维图像搜索处理和三维空间位置处理两类。其中,基于冠层高度模型(Canopy Height Model,CHM)识别单木是二维图像搜索处理数据中使用比较广泛的方法,森林冠层高度模型是一个表达植被距离地面高度的模型[14]。刘鲁霞等[15]对点云数据进行分层栅格化生成灰度图,通过Hough变换算法识别栅格图像图中的近似圆来确定单木位置；杜意鸿等[16]通过将分水岭算法分割后的油松冠状多边形与森林冠层高度模型重叠,搜索局部最大值,滤除树冠半径小于指定阈值的伪树冠顶点,得到最终的树冠顶点。但是,将点云数据转换为二维后,无法识别树干点与非树干点,造成Hough变换会在非树干点处识别出圆,因此,将点云转为二维数据的算法受到噪点的影响更大。三维空间位置处理相比较二维图像搜索处理更好地保存了点云的几何信息,对点云信息提取更精确[17]。Li等[18]通过利用点之间的相对间距以及通过定义适当的间隔阈值,从点云中依次识别树干;孙拱等[19]先拟合圆柱作为聚类中心,再计算点与聚类中心的欧式距离决定是否为同一树木的点。与二维图像搜索相比,基于三维空间位置处理数据的方式具有更好的抗噪性,更适合处理点云,但是在点云聚类的过程中,需要对点云数据逐点分析,聚类的阈值难以选取,导致树干点的识别精度较低,并且算法效率较低。

本研究以孟家岗林场落叶松人工林作为研究对象,在激光雷达扫描点云数据的基础上提出了一种多层K-means聚类的方式,提高原有算法的单木识别精度以及提高算法的效率。

1 研究区域概况与数据预处理

1.1 研究区域概况

研究区位于桦南县北部的孟家岗林场,地理坐标为北纬46°20′16″～46°30′50″,东经130°32′42″～130°52′36″,隶属佳木斯市林业局,行政区域属桦南县境内。林场地处完达山西麓余脉,以低山丘陵为主,坡度较为平缓,大部分坡度在10～20°之间。森林总面积约16 000km2,人工林始建于1956年,以落叶松(Larixgmelinii)、樟子松(Pinussylvestris)等针叶人工林为主,面积约占整个林分面积的2/3,其它为天然次生林,约占1/3,森林覆盖率达81.7%。孟家岗林场卫星地图如图1所示。

图1 孟家岗林场卫星地图

1.2 数据采集与数据概要

1.2.1背包激光雷达采集数据

本研究于2021年5月,使用背包激光雷达对实验样地进行扫描。当日天气晴,适合对数据进行采集。采集过程中以样地边缘一处作为起点,采集人员持设备以“S”型对样地进行扫描,最后从边缘处回到起点使扫描路线闭合。扫描所使用的设备参数如表1所示。

表1 背包激光雷达参数

1.2.2数据概要

实验样地是以落叶松构成的单层林,占地面积约760m2,样地内包含649株落叶松,郁闭度为0.6。经过背包雷达扫描后原始数据包含14 007 171个点,通过计算各点的平均最小距离值来计算点云的密度,计算公式如下。

(1)

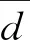
1.3 数据预处理

在森林点云数据中包含大量与树干无关的噪点,过多的噪点会明显影响算法的效率与正确性,因此,需要对数据进行去噪操作。

1.3.1地面噪点的去除

地面噪点是森林点云噪点中占比最多的噪点类型,本文采用RANSAC[20-21]算法进行地面点云数据的去除。首先,随机选取确定模型参数所需的最小点数求解模型参数；然后,去除大于预定阈值的点。如果小于阈值的点占集合中总点数的比例接近预定的阈值,则更新模型,重复N次保留最优结果。

1.3.2离群点的去除

激光雷达采集过程中会由于特殊原因采集到非树干且非地面的噪点,如飞行物等,这类噪点的密度远小于树干点,本文采用半径离群值去除该类噪点,删除在给定球形范围中密度小于阈值的点。

2 单木识别方法

2.1 点云水平分层

点云水平分层是为了解决森林点云数据中存在两个问题:

第一,点云数据的数据量过于庞大,而聚类中每次迭代都需要重新计算聚类中心,并且将点云数据从2类聚合为1类的时间也远大于从4类聚合为2类,以单木聚类为例,每次迭代的时间如图2所示。

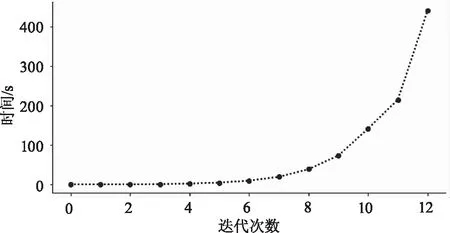
图2 算法收敛时间与迭代次数的关系

其中,测试所用的点云数据包含9 418个点,由图2可以看出,随着迭代次数的增加,每次算法的收敛时间也会增加。

第二,聚类中心的计算依赖于局部最大值,只对整体提取局部最大值会导致单木点云的过聚类与漏聚类。对点云进行分层计算,可以分别计算出各切片层的局部最大值,提高聚类的正确率,各个切片层之间的聚类结果也不会互相影响。当各层聚类完成后,以上下两层点云簇中心位置最近为合并条件,第一层与第二层合并,重新计算点云簇中心,再与第三层完成合并,重复此操作直至全部切片合并完成。

切片的层数可根据物体的形态,点云间的密度决定[16]。

2.2 多层K-means聚类识别单木

K-means是一种基于距离评价两个对象的相异度算法,传统的K-means算法仅依靠两个对象的距离来判断相异度,这种方法在森林点云数据的处理中存在问题:森林中树木之间存在大量的交叉,无法准确识别树木之间的交叉部分,为了解决这个问题,本研究在传统的K-means算法对相异度的评价上进行了改进。

2.2.1相异度M的计算

相异度是判断点云簇之间是否可以合并的标准,当两点云簇相异度低时,被视为同一物体的点云,在大多数使用K-means进行单木识别的研究中,点云簇之间的相异度计算只依靠点云簇之间的欧式距离[17-19],这样造成了属于多株单木的点存在交叉时错误聚类,本研究在计算相异度中引入了方向项作为另一个影响因子[22],这在一定程度上降低了异类点云交叉造成的错误聚类。

1)距离因子的计算。计算两个集合间的距离作为两集合之间的距离因子S,具体公式为:

S=d(pi,pj)

(2)

式中:pi,pj为两集合间欧式距离(Euclidean Distance)最小的点,d(pi,pj)为两点之间欧式距离,在三维空间中,欧式距离公式如下:

d(pi,pj)=sqrt((xi-xj)2+(yi-yj)2+(zi-zj)2)

(3)

式中:xi,xj为pi,pj的横轴坐标;yi,yj为pi,pj的纵轴坐标;zi,zj为pi,pj竖轴坐标。

2)方向因子的计算。以法向量为基础计算方向因子T,本研究中,法向量的计算基于K近邻估计,由某一点及其欧式距离最短的k个点估算平面,过该点作平面的垂线即为该点的法向量,k的数值由点云的密度决定。方向因子的计算如公式4所示:

(4)

式中:vi,vj分别为点pi,pj的法向量。

pi,pj的选择与计算距离因子中的点相同,vi,vj夹角计算公式如公式5所示:

(5)

式中:xi,xj为vi,vj的横轴坐标；yi,yj为vi,vj的纵轴坐标；zi,zj为vi,vj竖轴坐标。

最终,两点云集合相异度M计算公式如公式6所示:

M=S+ε×T

(6)

式中:ε为待定系数,用于方向因子与距离因子的平衡,当相异度M小于预定阈值时,点云集合视为相似点云簇,可以合并。

2.2.2点云局部最大值的计算

本研究区域中,以落叶松为主,在形态上接近圆锥体,对原始点云数据去噪后树干位置大致位于点云垂直投影的中心位置,在点云分层后,通过imregionalmax函数可以判断各层次在中心位置上的局部最大值点,其原理是找出当前区域内连通性最强的点,即找出在中心位置上的点,并且该点在近邻的点中连通性最强。

2.2.3多层K-means聚类流程

多层K-means聚类步骤如下:1)点云横向切片；2)分层输入点云集合；3)将点云集合中的每一个点初始化为一个集合,即P={p1,p2,p3,…,pn}初始化为P={{p1},{p2},{p3},…,{pn}}；4)初始化空集合C,视为已合并区,P为待合并区,计算P中相邻集合的相异度M,将P中相异度小于合并阈值的集合取出合并成新的集合放入集合C中,直至P为空时该步骤结束；5)将C中的元素重新放入P中重新计算相异度,合并后放入C中；6)重复“4)”-“5)”步骤直至函数收敛,其中函数收敛的条件为最后一次聚类输出的C与上一次聚类的输出C完全相等；7)不同层次点云合并。流程如图3所示。

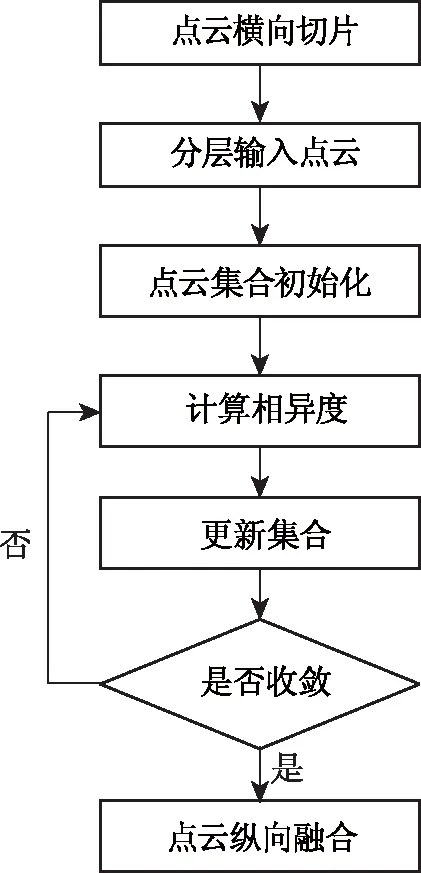
图3 多层K-means流程

3 实验与分析

本文使用Python与开源库Open3D进行实验,点的法向量以15个近邻点计算,相异度的计算中,距离因子与方向因子的平衡系数ε的值为0.3。

3.1 点云数据预处理结果

本文使用RANSAC算法和半径离群值去除地面噪点以及其他非地面且非树干的噪点,根据点云形态,半径离群值去噪的方式为在半径为2单位距离的球体中,点云密度小于20的点为离群点。原始点云、去除地面噪点、去除离群噪点分别为图4—图6所示。

在图5中,黑色部分为地面点云,红色为非地面点云,在图6中,红色为未聚类的单木点云,蓝色部分为去除的离群点。

图4 原始点云

图5 去除地面噪点

图6 去除离群点

3.2 多层K-means聚类结果

改变聚类的层数会对识别单木的精度产生影响,如果分层较多会使单层点云密度小,聚类后的单木形态不准确,如果层数少则会影响局部最大值的位置,当一个点云簇距离该层的局部最大值较远时，会造成相异度较大,导致本属于该树木的点云无法聚类。 以单株树木聚类为例,使用不同层数进行对比实验,其中测试使用的单木点云包含9 418个点。测试结果如表2所示。

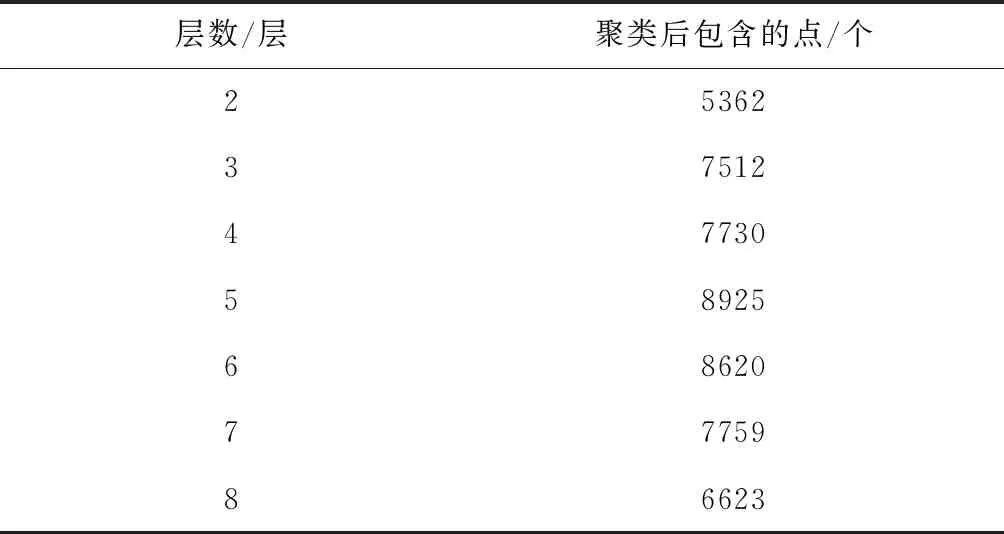
表2 不同层数对识别单木精度的影响

由表2可知,当层数为5时,单木的精度最高。

同时,不同的层数对算法的识别率也有影响,不同层数在原始数据去噪后的单木识别率如表3所示。

由表3可知,当层数为7时,算法的识别率最高,但是在考虑单木聚类精度的情况下,本文选择将点云分为5层进行实验。

在计算结束后,将所有聚类结果展示在三维空间中,聚类的效果如图7所示。

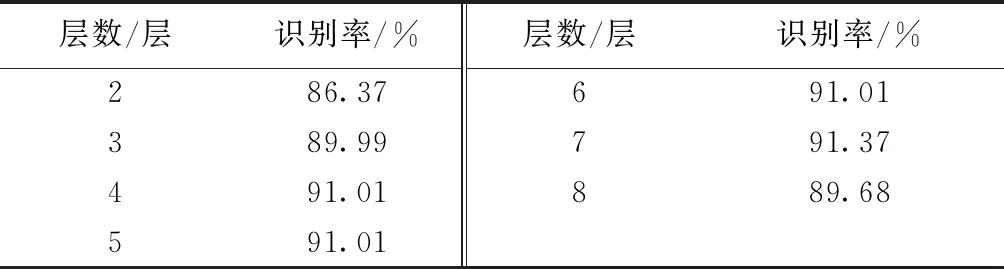
表3 不同层数对树木识别率的影响

图7 点云聚类结果

实验样地共有649株树木,经过与原始点云的比对,其中,未能被识别的单木有32株,将不同单木识别为同一单木的情况有4类,共有59株单木识别失败。未能被识别的单木与不同单木识别为同一种单木的案例如图8—图9所示。最终将被识别树木与实验样地调查的数据比对,未发现将其他物体识别为树木的情况。

图8 未能被识别的单木

图9 将多株单木识别为同一单木

结果的统计如表4所示。

表4 实验结果的统计

经过观察原始点云,未能识别的单木主要原因在于被其他树木遮挡严重而导致点云稀疏,经过半径离群值去噪后点云数量过少,点与点间距离过大,导致无法被聚类。而被聚类成同一单木的多株单木，是由于树木之间交叉过于密集造成的。

3.3 多层K-means与单层K-means对比

在保持点云数据点的数量一致、算法参数一致的情况下,分别使用多层K-means与单层K-means进行聚类,算法的收敛时间如图10所示。

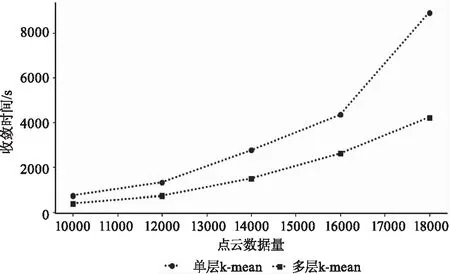
图10 多层K-means与单层K-means收敛时间对比

在同一数据集下,多层K-means与单层K-means的单木识别识别率对比如表5所示。

表5 同一数据集中多层K-means与单层K-means的效果对比

由图10和表5可知,多层K-means从收敛时间与聚类效果都优于传统的单层K-means。

4 结束语

以点云数据为基础获取森林信息,是对森林结构准确测算的重要手段之一[23],准确的单木识别是这些研究的基础,本算法在传统K-means聚类的基础上进行了分层处理,添加了K-means聚类条件,降低算法的收敛时间,提高单木点云聚类的准确率,得出结论如下:

1)对点云进行切片操作可以提升聚类的准确性,降低算法的收敛时间,切片操作大幅度减少了单次聚类所需要计算的点,计算后只需对不同层的同一类点云拼接就可以得到单木的点云。由于聚类算法的特性,聚类中的一次错误聚类就会导致聚类中心的计算错误,从而导致了后续继续依照错误的中心进行聚类,导致聚类错误的点数增加,而对点云进行分层,可以分别计算不同层次的点云中心,避免了不同层次间聚类中心互相影响。

2)在相异度的计算中,使用以法向量为基础计算方向因子可以更充分地考虑点云中不同点云簇间的关系,在一定程度上解决了不同单木之间交叉的问题。

3)本聚类算法不进行圆柱拟合等操作,因为对于较为稀疏的点云数据来说,点云的缺失会导致树干部分无法拟合圆柱而导致漏检测的情况,本算法逐点进行计算,确保所有点均被考虑,不被树干形态所影响。

4)森林结构是森林经营管理的重要依据,精准的森林结构参数可以使相关从业人员判断该森林中单木的情况,从而提高林分质量,充分发挥林地生产力。