基于三维数字图像相关法的非接触式动态位移测量方法研究

南 亨，唐忠林，赵伟博，谭伟杰

(1.陕西工业职业技术学院 航空工程学院，陕西 咸阳 712000；2.贵州大学 公共大数据国家重点实验室 大数据产业发展应用研究院，贵阳 550025)

0 引言

在动力学试验中,测量物体位移的方法是保证试验品质的重要环节,目前的位移获取方法大体上可以分为两类,分别为接触式测量与非接触式测量。其中，在接触式测量中，所使用的的传感器包括速度传感器、加速度传感器等;非接触式传感器包括激光位移测量器、全球定位系统(GPS, global positioning system)、光学测量等。T.Uchiyama等人将激光位移计与加速度传感器结合，用于肌力图(MMGs, mechanomyograms)的系统辨识[1]；A.Tezuka等人将激光位移计用薄膜振动实验[2]；I.Godler等人通过旋转的方式扩大了传感器的测量范围[3]；上述研究均获得了良好的效果，但是受限于激光位移计和加速度传感器的本身特点，该类方法具有一定的局限性。Ding等人运用了GPS系统监测地面上大型物体结构的变形运动，达到了预期的试验结果[4]；但由于GPS往往适用于大型物体的测量，所以在小型实验中并不能很好的监测数据精度，因此并不适用于小型实验。

在国外研究方面，1980～1990年期间，相关研究者提出了基于数字图像相关法(DIC, digital image correlation)的非接触式光学测量方法。如今,结合机器视觉技术,三维数字图像相关法[5-6](3D-DIC, 3-Dimensional DIC)应运而生,该方法突破了二维方法的限制,可以测量物体的三维形貌和变形,极大的扩展了该方法在工程测量中的应用。随着数字相机分辨率的提升和图像处理方法的改进,3D-DIC方法因具有非接触、可全场测量、测量精度高、使用方便、采集数据信噪比高等优点[7],现已成为实验力学的重要组成部分,并在光学测量中被广泛使用[8-10]。

在国内研究方面，王静等较早的将数字图像相关技术应用于桥梁缝隙变形监测中[11]；潘兵等将数字图像相关技术应用与面内拉伸简单的位移测量[12]；马永尚等利用3D-DIC观测系统研究压缩状态下花岗岩岩板的破坏全过程,得到了三维全场位移和应变[13]；陈亚军等将三维图像相关技术应用与材料形变之中[14]；翟启云等利用三维数字图像相关发测量了复合材料泊松比[15]；李湘萍等利用三维数字图像相关技术，对无人机机翼的压载变形过程进行了追踪[16]；吴凤琳等通过数字图像相关法对观测板状试样剪切应变场进行观测，并与引伸计法进行比较[17]。

上述研究大多数针对于被测物在被测平面内进行运动的，多为平移，拉伸、压缩等运动形式。本文基于DIC技术的基本原理和方法，搭建了基于三维数字图像相关技术的非接触式测量平台，并进行了动力学试验中的动态位移的测量，运动形式为沿相面法向移动和绕相面横轴旋转。通过文中实验，验证了基于数字图像相关技术的测量方法的适用范围。

1 基本原理

在提出的测量方法中，获取被测物动态位移的具体过程如下：图像获取、相机参数标定、图像相似度匹配、三维重建。

1.1 图像获取

在三维数字图像相关技术的图像获取环节中，需要保证两个不同的相机拍摄时间应当是同步的，即相机需要同时触发，同时拍摄。因此，在两个相机的触发同步性上，有着很高的要求，常规的人为控制触发难以满足精度需求。一般情况下，采用外部的电平信号器进行触发，经测试其精度可以达到预期需求。在采集过程中，为了提供图像匹配特征，通常用喷漆对被测物表面进行处理，使其具有随机的灰度分布。

1.2 相机参数标定

相机参数标定的过程是利用不同位置的两个相机对标定板的不同姿态位置进行多次拍摄，从而根据相对关系，得到相机的内部参数及外部参数，包括相机相对位置，平移矩阵及旋转矩阵等。本文中主要采用张正友标定法[18-20]。该方法是张正友等人于2000年左右提出的，在要标定的平面靶标上有很多方格点，标定方格如图1所示。

图1 平面标定方格

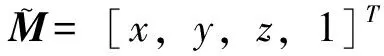
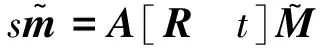
(1)

其中：s为任意的非零尺度因子，旋转矩阵R与平移向量t为相机的外部参数矩阵，A为相机的内部参数矩阵。

1.3 图像相似度匹配

图像匹配主要利用子区匹配的方法，其具体过程为：在需要测量的图像上，以待测点为中心，划定一定区域作为参考子区，并且找到这个参考子区在目标图像上的对应目标子区，目标子区的中心位置即为待测点在目标图像中相对应的位置。在子区划分时，为了提高区分程度，被测物表面往往需要足够的、不重复的、随机的纹理图案。目前最常用的包括散斑图像和标记点，如图2所示。

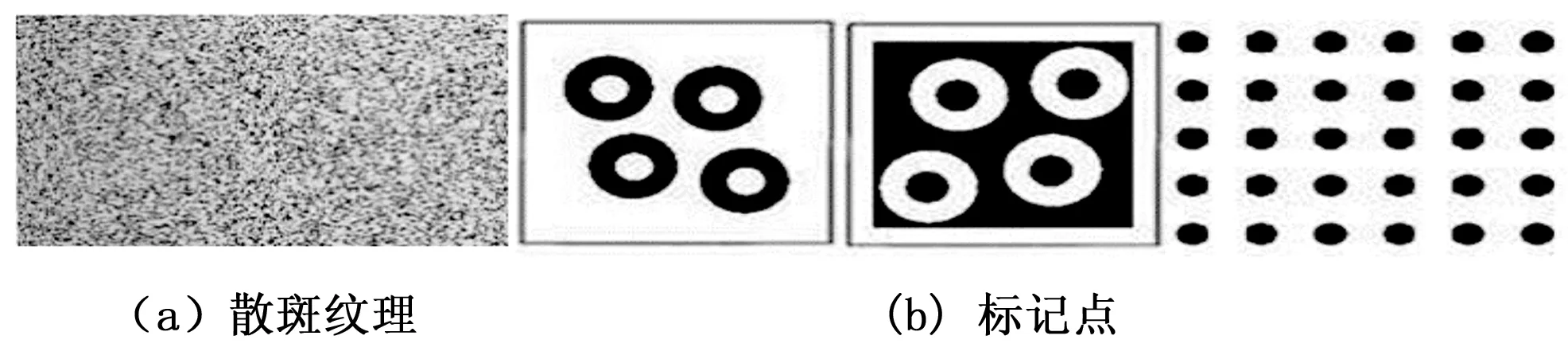
图2 被测物空间纹理实例

相关函数是用于度量两个区间的相似程度的函数，该函数直接影响了最终的测量结果。依据不同准则有着多种不同的相关函数，若以难易程度划分，则最为简易的被称为最小平方距离函数(SSD， sum squared difference)：

(2)

其中:f(x,y)、g(x′,y′)为参考子区间和预期子区间内对应的灰度数据。该函数即为参考区域和目标区域的匹配性。但是，各种复杂的环境因素会影响匹配的准确性，环境因素包括曝光度、角度、图像畸变及噪音等因素，在环境因素的影响下，基于SSD的相关函数的匹配性会受到很大的影响。所以，需要对该相关函数进行修正，使其具有一定的稳定性，修正如下：

(3)

其中:a和b用来描述外界光强可能发生的线性变化。

1.4 三维重建

图3 图像坐标系

如图3所示，首先创立一个直角坐标系O0-uv，(u,v)，它表示的坐标系是以图像中的像素作为单位的。其次，创立第二个坐标系，这个坐标系对应的是物理空间并且与第一个坐标系平行，图中(X，Y)表示以毫米为单位的图像坐标系的坐标。如果O1在u,v坐标系中的坐标为(u0,v0)，每一个像素在X轴与Y轴方向上的物理尺寸为dX、dY，则图像中任一个像素在两个坐标系下的坐标有如下关系：

(4)

用齐次坐标和矩阵形式可表示为：

(5)

由于摄像机可以安放在环境中的任意位置，故需建立一种坐标系来描述。摄像机和环境中其他物体的位置，称为世界坐标系O-XWYWZW。摄像机坐标系和世界坐标系的关系可用旋转矩阵R与平移矩阵t描述。取空间中任一点，存在如下关系：

(6)

将以上所得世界坐标系与图像坐标系的对应关系分别应用左右两个摄像机，如图4所示。

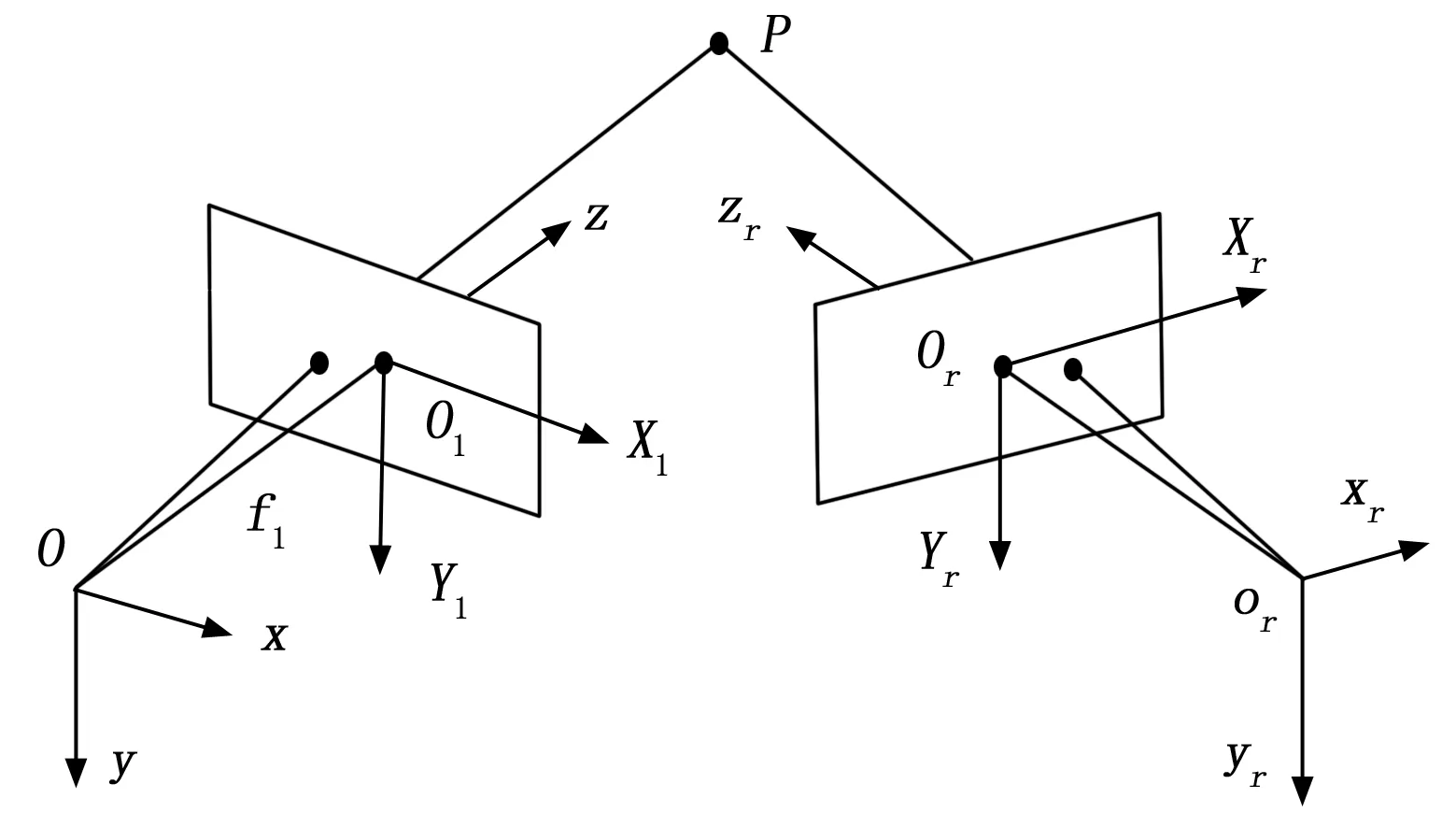
图4 空间三维点重建

如果不知道相机与世界坐标的变换关系，则无法求解，因此，假设左侧相机为世界坐标的零点，则对于位于右侧的像机，则有如下坐标变换关系：

(7)

然后，对于左摄像机，由于其位于世界坐标系的原点处且没有旋转，故R为单位阵，t为零列阵，u0t=v0t=0，其图像坐标系与世界坐标系的关系如下：

(8)

2 关键技术实现

基于上文中所提到的数字图像相关法的基本原理，搭建了一种应用于动力学试验中的3D-DIC测量系统。

本文使用的测量系统，由以下几部分组成：两个Point-Grey公司生产的高速相机、无频闪光源，信号发生器、USB3.0数据传输线、Point Grey FlyCapture图像采集软件及用于图像存储和处理的计算机、被测物组成。

本试验搭配的电平触发器一般设置为占空比为50的方波信号，采样频率设置为250 Hz。外接电平触发器采用单片机实现高电平触发，可通过程序控制保证双相机同时触发，本试验设置为一次性采集1 500张图像，即每次触发采集6 s的图像数据。图像处理及位移/应变分析采用自行构建编写的软件进行，如图5(a)为软件的主要功能界面和分析流程图，该软件可实现相机标定、图像匹配、应变场计算和动态位移三维重建等功能。

如图5(b)所示，进行试验的时候，根据双目视觉原理，两个相机位于不同的位置，存在一定的夹角，并且保证被测物在相机的拍摄范围之内。采用外接的电平信号触发器是为了保证两个相机的同步触发，在光源不足的环境里，需要提供无频闪光源，保证相机的曝光率，提高采集的图像质量。

图5 图像处理软件

2.1 标定板图像采集与相机参数标定

将测量系统组装完毕后，首先进行相机参数的标定，标定板如图1所示，将标定板以不同的姿态放置，随后通过两个不同位置的相机对标定板进行采集，如图6所示。

图6 相机采集的标定板图像

采集完成之后，相机的内外参数标定利用Matlab-Stereo Camera Calibration工具箱进行，通过导入不同相机的标定板图片，可以得到不同相机中不同图像的重投影误差和针对标定板的两相机的位置关系，如图7所示。

在对大数据技术进行合理应用的过程中，可有效提高其通信范围，使用户通过及时的交流对问题进行解决，从而提升远程教育的综合效果。大数据技术还使得教学的方法多样化，学生可以根据想学的内容对课程进行选择，节约了学习时间，能够找到学习中的重点，并且进一步提升了学习质量，提高了学生学习过程中的代入感。

图7 重投影误差和相机位置关系

保存并输出标定的相机参数，包括每个相机的内部参数(焦距和主点坐标)和两相机相对的外部参数(旋转矩阵和平移矩阵)。其标定参数示例如下：

>> stereoParams.CameraParameters1.PrincipalPoint

ans=

991.9426 884.1584

>> stereoParams.TanslationOfCamera2.

ans=

-410.4175 -25.0669 20.5043

>> stereoParams.CameraParameters1.FocalLength

ans=

1.0e+03*

3.7706 3.7682

>> stereoParams.RotationOfCamera2.

ans=

0.9617 0.0202 -0.2735

-0.0260 0.9995 -0.0177

0.2730 0.0241 0.9617

2.2 图像采集与子区匹配

在进行相机标定完成后，保持原有的相机位置不变，继续对需要测量的物体进行拍摄采集，为了保证测量的同步性，采用上文提到的外部触发器进行触发，让两个相机在同一时刻进行图像采集。图8和图9分别表示两种不同被测物图像示例。

图8 双相机图像采集示例(1)

图9 双相机图像采集示例(2)

在上述采集的图像中，选取某一区域作为匹配子区，以初始图像中的子区作为参考，在模型动态变化过程中，观测所选择的子区对应点的变化，即可得到每张图像中相关点的位置关系，基本原理如图10所示。

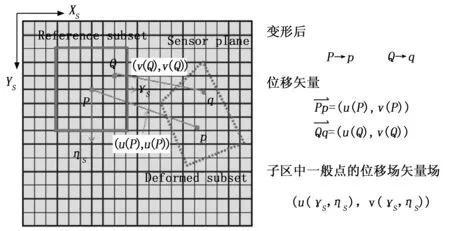
图10 子区匹配示意图

综上，结合相机标定的内外参数，结合子区匹配得到的位置信息数据，然后对所检测的点进行三维重建，即可得到相应的位移信息。

3 试验结果与分析

基于上文搭建的测量系统，设计了两个不同类型的实验，并分别进行了图像获取、相机参数标定、图像相似度匹配、三维重建，随后将实验结果与真实结果进行对比，说明了该测量系统的精度和适用范围。具体实验如下：

实验1:像面法向移动测量实验

本组实验的运动形式为被测物沿像面法向移动，采用单轴步进伺服电机作为运动部件，实验系统由步进电机，控制器，被测物组成。通过控制器设置电机的运动幅值及速度，从而使试验件按照预期的形式运动。

利用相机标定得到的相机内外部参数和图像匹配得到的监测点在图像坐标系中的位置信息，对该监测点进行三维重建即可获得其在法向的变形值，即法向位移。在本实验中，设置步进式电机做循环往复运动，运动幅值为10 mm，高速相机拍摄频率为250 Hz，拍摄时间为6 s，总拍摄张数为1 500张，使用3D-DIC系统对被测物进行连续3次拍摄，分别记为T1、T2、T3，结果如图11所示。

图11 第一次实验响应结果

图中3条曲线分别代表被测物表面某一标记点的3次位移结果，由于采集时刻的不同，各曲线之间存在相差，但不影响幅值结果。由表1可以看出，3次实验结果之间相差不大，具备良好的精确性，与真值10 mm的误差均很小，具备良好的准确性。

表1 第一次实验结果对比

因此，通过本次试验可以证明，3D-DIC系统在对被测物像面内法向运动时的位移捕捉精度很高，可以满足试验要求。

实验2：像面旋转运动测量实验

系统运用于部分动力学试验中时，除了观测被测物沿着法向运动的状态，还需关注被测物的绕被测平面横轴的偏转角度，当偏转角度过大，会引起视角不清晰，图形畸变等原因，难以准确捕捉运动轨迹，因此，通过本试验，确定该测量系统的角度适用范围。

本实验采用的器械为AX-12A型小型舵机，将被测的平板与舵机连接，并在平板上设置标记点，用于拍摄，该舵机转角度范围为0～360°，并且可以实现以任意角度为平衡位置做定轴往复运动，因此，可以满足试验需求。

首先，设置舵机角度，使其平衡位置与相机平面平行，即垂直于拍摄光轴，设置舵机旋转角度为偏离平衡位置5°，运动角度范围为10°，图12为舵机运动示意简图，经测量，被测平板长度AB为40 mm，则由三角函数关系可得运动范围BC为6.96 mm，运动幅值为3.48 mm。

图12 舵机运动示意简图

对被测物进行3次拍摄，分别为T1、T2、T3确定角度的使用范围，第一次拍摄，使被测平板平衡位置完全垂直于相机光轴，即垂直于地面；第二次使平板与光轴夹角为83°，即偏离垂直位置7°；第三次使平板与光轴夹角为75°，即偏离垂直位置15°。虽然平衡位置发生了变化，但是3次试验的运动幅值都为±5°，3次的结果如图12所示。

表2 第二次实验结果对比

由图13和表2可知，该测量系统对角度的把握比较准确，即使在±15°的平衡位置、±20°的运动幅值下仍能准确捕捉动态位移信息。随后，又进行了若干次不同角度的实验，最终确定，当运动幅值小于20°时，所捕捉的结果都比较准确，当运动幅值大于20°时，效果会变差。因此，在使用该系统时，尽量保证被测物在法向的偏转角度小于20°。

图13 第二次实验响应结果对比

4 结束语

本文搭建了3D-DIC测量系统，并通过地面实验，对测量系统的精度和适用范围进行了验证。主要结论如下：

1)搭建了基于数字图像相关技术的光学测量系统，其基本原理为：图像获取-相机参数标定-图像相似度匹配-三维重建，其中图像采集是利用不同位置的相机采集模型的运动图像，相机参数标定是为了获取两个相机的内、外部参数，图像匹配是为了获得不同时刻的图像中的监测点在相机中的图像坐标，三维重建是利用小孔成像原理将图像匹配的结果转换为每个检测点随时间变化的物理位移。

2)为了验证该测量系统的精度和可靠性，将该测量系统应用于像面法向移动，将测量结果与实际位移进行了对比，验证了该测量系统的精度；随后在像面旋转运动中，验证了测量系统的拍摄角度范围，结果表明，在偏离角度小于20°时，结果较好。

综上，基于数字图像相关技术的测量系统具有较高的精度和可靠性，测量偏离角度在20°以内时，效果良好，能满足一般动力学实验的要求。