基于改进的卷积神经网络的步态识别

钱 兴，张晓明，2，郝子浩

(1.中北大学仪器与电子学院，太原 030051；2.中北大学仪器科学与动态测试教育部重点实验室，太原 030051)

0 引言

步态识别是一种新兴的生物特征识别技术，旨在通过人们走路的姿态进行运动状态的识别。随着智能硬件的发展，基于惯性传感器采集到的步态序列数据可以用来识别穿戴人员的位置和运动信息，主要应用在单兵作战导航和楼宇内导航定位等领域。显然步态的识别和分类具有重要意义，而目前关于惯性传感器采集到的序列数据中步态识别研究很少，因此设计一种针对序列数据的步态识别方法很有必要。

微机电系统(Micro-Electro-Mechanical System， MEMS)惯性传感器具有潜在的成本、尺寸、质量等优势，其采集到的序列数据信息量大、输出信息实时性强，使其更适合应用在步态识别中。A. H.Johnston等运用智能手表内置的加速度传感器与陀螺仪对人员进行实时识别，结果证明加速度传感器优于陀螺仪。但三轴加速度传感器对运动太过敏感导致步态周期划分不准确，从而导致步态识别率不高。近年来，卷积神经网络(Convolutional Neural Networks，CNN)自提出以来，就凭借其在分类识别中展现出的优势而受到了广泛关注。已有研究人员利用CNN提取智能手机信号来识别人体步态，但由于仅使用手机加速度传感器，其识别准确率和实时性都有待进一步提高。也有研究人员将CNN成功应用于脑电信号的特征提取并进行运动分类，但由于脑电信号微弱且稳定性较差，目前无法实际应用。陈法权等采用多种惯性传感器组合进行步态识别，虽然增多传感器能提高特征数量，但不同步态之间的相互干扰也相应增多；另外其采用的激励使用ReLU函数，该函数对输入阈值小于0 的神经元有抑制作用，因此识别率仅为91.5%。

针对上述问题，1)本文采用了加速度传感器与弯曲度传感器组合获取人体运动信息。弯曲度传感器是一种测量弯曲角度的装置。弯曲度传感器是由一种可变电阻组成的，覆盖在弯曲度传感器的表面，不同的弯曲角度会改变弯曲度传感器的电阻值，根据弯曲度传感器的电阻值变化即可判断弯曲角度。弯曲度传感器放置在膝盖位置能够很好地采集到人体膝盖弯曲程度的信息，并对步态周期进行精准分割，解决了三轴加速度传感器步态周期划分不准确的问题；弯曲度信息与三轴加速度信息的组合能够很好地对不同步态的特征值进行区分，从而提高识别率。2)设计了一种激励层改进的CNN步态分类模型以进行步态特征值的自动提取，改进后的激励层采用了带泄露线性整流函数，该函数负数端斜率为一个常数，能够解决遇到卷积输出数据小于0时神经元被抑制的问题。最后，通过实测数据集进行了学习和验证。

1 步态数据的获取与算法优化

1.1 步态数据的获取

在步态数据采集单元中采用了加速度传感器与弯曲度传感器组合检测系统，此系统包括三轴加速度传感器和弯曲度传感器。传感器安放位置如图1所示，三轴加速度传感器放在大腿靠近膝关节处(轴朝人体前方，轴沿腿向下)，弯曲度传感器放在膝关节处。图2～图6分别表示传感器采集的五种步态模式，即走路、上下楼和上下坡的部分数据。从图中可以看出，弯曲度传感器采集到的数据每经历一次波峰即完成一次步态周期，同时对应着不同运动状态的三轴加速度传感器中的轴、轴、轴数据也各不相同。弯曲度数据在步态周期划分中具有独特优势，但特征少，无法单独用来步态识别；而三轴加速度传感器步态周期划分不准确，单独进行步态识别时识别率较低。因此可以通过两者结合进行步态分类。

图1 传感器安放位置Fig.1 Sensor placement position

图2 传感器采集的步态模式：走路Fig.2 Gait pattern collected by sensor:walking

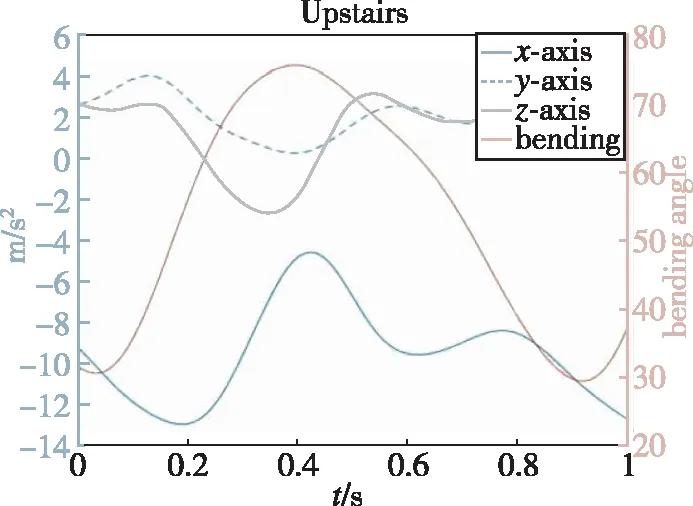
图3 传感器采集的步态模式：上楼Fig.3 Gait pattern collected by sensor:upstairs

图4 传感器采集的步态模式：下楼Fig.4 Gait pattern collected by sensor:downstairs

图5 传感器采集的步态模式：上坡Fig.5 Gait pattern collected by sensor:upslope

图6 传感器采集的步态模式：下坡Fig.6 Gait pattern collected by sensor:downslope

1.2 步态信号的表示

在传感器采集到的信号中，定义加速度步态数据向量=[,,,,,]，弯曲度步态数据向量=[]，=1,2,3,…,,是分割后步态信号的序列长度。由此构成了步态信号的×4输入矩阵

=[,]

(1)

采集到的矩阵数据在同一时刻具有相互关联性，在不同时刻的同一传感器数据在时间上也有关联性，提取出的特征更能表示原始步态的信息。

1.3 CNN基本原理

CNN是一类包含卷积计算且具有深度结构的前馈神经网络，是深度学习的代表算法之一。其隐含层内的卷积核参数共享和层间连接的稀疏性使得CNN能够以较小的计算量处理类似网格结构的数据，三轴加速度传感器和弯曲度传感器采集到的序列数据为二维矩阵，适合用CNN提取数据特征和进行步态识别。典型的CNN模型主要由输入层、卷积层、激励层、池化层、全连接层和输出层组成。

输入层主要是将1.2节得到的×4输入矩阵作为CNN的初始输入，将数据传输到卷积层进行计算。

卷积层主要是对输入层传输过来的步态数据进行步态特征值提取，卷积层中包括多个卷积核。通过对每一层的数据与卷积核做矩阵元素乘法求和并叠加偏差量，生成包含原始数据部分特征的步态矩阵。每一层的计算如下

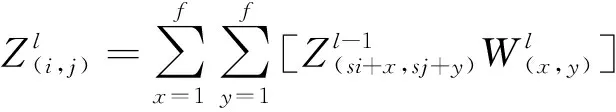
(2)

(3)

其中：为第层输出；-1为第层输入；(,)为对应特征值的大小；为当前层卷积核；-1为当前层的偏差量；(,)为卷积核的大小；、代表卷积核行列数；代表卷积的步长；代表填充层数；(,)代表的大小。

激励层是将卷积层输出结果做非线性映射，因为卷积层的计算是一种线性计算，对非线性情况无法很好拟合。有时也会把卷积层和激励层合并在一起称为卷积层。激励层一般采用线性整流函数(Rectified Linear Unit, ReLU)作为其激励函数。

池化层主要进行特征选择和信息过滤，主要目标是降低卷积层提取出的特征值信息。大多数情况下，最大池化性能更优。特征矩阵从激励层传入到池化层，池化层将保留局部区域的最大值，其操作定义如下

=Max(-1)

(4)

其中，Max表示池化层进行最大池化操作。

全连接层(Fully Connected Layers，FC)在整个CNN中起到分类器的作用。如果该层的输入是一个序列，则全连接层在每个时间步上独立地起作用。全连接层通常设置为固定的神经元数。

输出层的上游是全连接层，通常使用逻辑函数或归一化指数函数(softmax function)输出分类标签。

1.4 CNN激励层的改进算法

CNN的激励层通常使用线性整流函数，如图7所示，定义如下

图7 线性整流函数Fig.7 Rectified linear unit

=max(0,)

(5)

但ReLU负数端斜率为0，使得卷积输出的数据在负数部分无法表达出来，导致神经元不能更新参数。步态的卷积层输出的数据中含有负数部分，因此ReLU就不适用了。负数部分能否在激励层中表达出来，是提高步态识别率的重要一步。为了解决这一问题，本文采用带泄露线性整流函数(Leaky ReLU)对激励层进行改进，如图8所示，定义如下

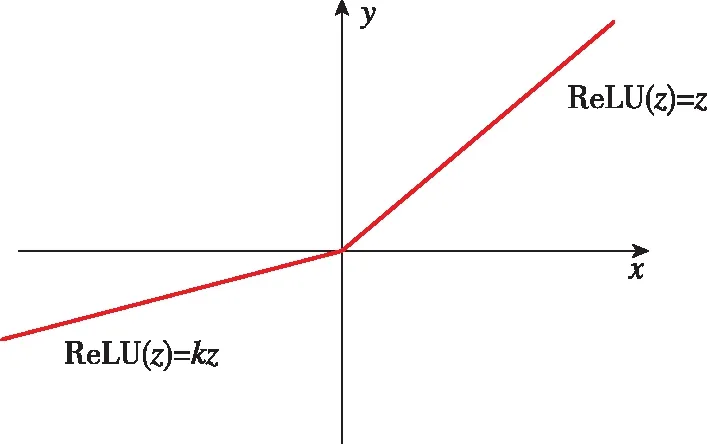
图8 带泄露线性整流函数函数Fig.8 Leaky rectified linear unit

=max(,)

(6)

该函数负数端斜率为一个常数，是根据实际经验来取值，文献[17]进行了大量的实验，验证了取值范围在0～0.5内时，Leaky ReLU能够让神经元在负数部分进行参数更新，达到对CNN的激励层进行优化的目的，同时提高了步态的识别率。

2 基于CNN的步态识别模型

2.1 CNN步态识别模型的构建

采集到的三轴加速度传感器数据与弯曲度传感器数据在同一时刻具有相互关联性，人体步态的特点是在不同时刻的同一传感器数据在时间上也有关联性。根据这些特点本文针对性地设计了一个基于CNN的步态识别优化模型。此模型由9层构成，如图9所示，各层介绍如下。

图9 CNN步态识别模型Fig.9 CNN gait recognition model

(1)输入层

将×4的步态数据矩阵作为CNN的输入层，其中是分割后步态信号的序列长度，4分别为三轴加速度传感器中的轴、轴、轴数据与弯曲度传感器中的弯曲度数据。

(2)卷积层1

将滑动卷积滤波器应用于输入。卷积层1的卷积核大小设置为：高度3，宽度1，步长设置为1，卷积核层数设置为6，处理后得到6个98×4的特征矩阵。

(3)激励层

采用Leaky ReLU对卷积后的数据进行处理。

(4)池化层 1

将激励层数据作为池化层的输入。最大池化层的树池是一个2×1矩阵，步幅为1。经过处理后得到6个97×4的特征矩阵。

(5)卷积层2

卷积层2的卷积核大小设置为：高度 5，宽度 1，步长设置为1，卷积核层数设置为12，处理后得到12个93×4的特征矩阵。

(6)激励层

采用Leaky ReLU对卷积后的数据进行处理。

(7)池化层 2

最大池化层的树池是一个3×1矩阵，步幅为1。经过处理后得到12个91×4的特征矩阵。

(8)全连接层

全连接层设置为4368个神经元。

(9)输出层

采用Softmax函数作为步态类型的输出，主要作用是输出数据对应五种步态的概率值，概率最大的就是当前人体运动的步态。

2.2 CNN步态识别模型的训练

CNN训练包含了2个过程：正向传播和反向传播。使用现有的数据进行正向传播，计算出损失函数值，然后再进行反向传播。卷积层的反向传播是一个与前向传播类似的交叉相关计算

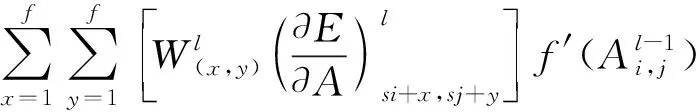
(7)

(8)

其中：为代价函数计算的误差；′为激励函数的导数；为学习速率；根据反向传播可以更新卷积核数值。本文CNN的误差函数选择的是Softmax。池化层在反向传播中没有参数更新，因此只需要根据池化方法将误差分配到特征值的合适位置即可。CNN通常使用BP框架内的随机梯度下降和其变体，本文采用的是Adam算法，相较于其他算法更适合解决含大规模数据和参数的优化问题。

3 实验和结果分析

3.1 实验数据

实验测试人员14名，其中男女各7人，均无任何影响走路状态的疾病。中国成年男性平均身高为169.7cm，成年女性平均身高为158.6cm。故选择，男性7名，身高在 165～185cm 之间；女性7名，身高在 155 ～170cm 之间。分别测试走路、上下台阶、上下坡(45 °)。传感器采集的数据量如下：走路4000s、上下台阶各4000s、上下坡各3800s。

实验使用的传感器的采样频率为100Hz，正常人走路1min大约在100～120步，故一个步态周期大约在1s左右，所以选定每100个数据为一个周期进行数据处理，即步态长度=100。

3.2 实验结果及分析

实验使用90%的数据作为训练组，用于进行CNN模型的训练;剩下的10%作为验证组，用于验证CNN模型的准确程度。

3.2.1 模型参数对识别效果的影响

卷积核层数和卷积核大小对CNN步态识别率的影响,如表1和表2所示。

表1 卷积核层数的影响

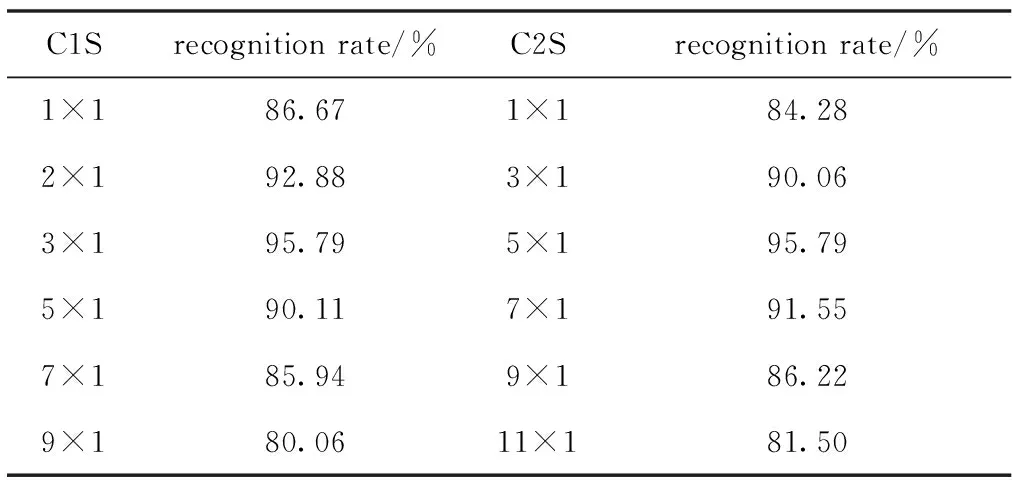
表2 卷积核大小的影响

表1中，C1L代表卷积层1的卷积核层数,C2L代表卷积层2的卷积核层数，recognition rate代表此时的步态识别率。将卷积层1的卷积核层数分别调整为2、3、4、5、6、7、8、9、10层，其他相关参数如池化层参数等不进行改变。从识别率中可以看出，当卷积层1的卷积核层数为6时识别率最高。将卷积层2的层数分别调整为4、6、8、10、12、14、16、18、20层，其他相关参数同样不进行改变。从识别率中可以看出，当卷积层2的卷积核层数为12时识别率最高。

表2中，C1S代表卷积层1的卷积核大小,C2S代表卷积层2的卷积核大小，recognition rate代表此时的步态识别率。将卷积层1的卷积核分别调整为1×1、2×1、3×1、5×1、7×1、9×1，其他相关参数不进行改变。从识别率中可以看出，当卷积层1的卷积核为3×1时识别率最高。将卷积层2的卷积核分别调整为1×1、3×1、5×1、7×1、9×1、11×1，其他相关参数不进行改变。从识别率中可以看出，当卷积层2的卷积核为5×1时识别率最高。由于矩阵之间的关联性，3×1和5×1的卷积核适合处理步态数据的大小，从而达到最优地提取数据特征的目的。

在激励层改进过的CNN模型中改变Leaky ReLU的值，由于取值范围在0～0.5时效果达到最佳，故选择0、0.01、0.05、0.1、0.5，观察值对步态识别率的影响，如表3所示。

表3 k值的影响

表3中，取值分别为0、0.01、0.05、0.1、0.5。从数据中可以看出，改进后的CNN识别模型随着取值增大呈正态分布，在=001时识别效果达到最好。

3.2.2 改进前后CNN模型的比较

将激励层改进过的CNN模型与未采用弯曲度传感器改进过的CNN模型和未改进的CNN模型进行比较。未改进的CNN模型只将激励层Leaky ReLU替换为ReLU，其他参数不改变，观察对步态识别率的影响，如表4所示。

表4 改进前后CNN模型的比较

表4中，将未采用弯曲度传感器的CNN识别模型、未进行激励层改进的CNN识别模型，与激励层改进过的CNN识别模型进行对比，发现激励层改进过的CNN识别模型效果明显提升。

从上述实验可以得知，卷积层1的卷积核大小为3×1，层数为6；卷积层2的卷积核大小为5×1，层数为12；Leaky ReLU的值为0.01时CNN识别模型的识别率达到最优，最优识别率为95.79%。

4 结论

本文提出了一个利用改进后的CNN方法实现对序列数据的步态分类方案。

1)搭建了一个三轴加速度传感器和弯曲度传感器的检测平台，能够很好地对不同步态的特征值进行区分。实验结果表明：相较于未采用弯曲度传感器的CNN模型，步态识别率提高了4.78%。

2)设计了一种改进后的CNN模型实现对步态的分类。实验结果表明：改进后的CNN识别率达到了95.79%，相较于未改进的CNN模型识别率提高了3.37%。同时为实现单兵作战导航和楼宇内导航定位中惯性器件的步态识别提供了解决方案。

本文选定每100个数据为一个周期进行数据处理，而对不同人群的步态频率是不相同的，为了分析序列数据的步态识别特性，提高步态分类的准确程度，今后的工作重点是数据分割；与此同时，扩大不同人群的数据样本，提高方案的通用性、准确性和鲁棒性。