基于马尔可夫决策的穿越沙漠游戏策略研究
2022-03-30邓晨晨黄宇轩齐泽坤杨松
邓晨晨 黄宇轩 齐泽坤 杨松
摘要:“穿越沙漠”游戏是一款综合考虑资金、资源、天气、时间、博弈等多种因素在内的复杂策略游戏。文章将基于图论与马尔可夫决策有关模型,分析讨论玩家在未来信息已知与未来信息未知两种情形下的最优策略。该模型综合考虑了风险评估与多阶段决策理论,可为优化算法与企业决策提供一定借鉴意义。
关键词:沙漠掘金;图论;动态规划;马尔可夫决策;最优化理论
一、引言
“穿越沙漠”游戏是一款综合考虑资金、资源、天气、时间、博弈等多种因素在内的多阶段策略游戏。游戏要求玩家在沙暴天气原地停留、到达矿山当天不许挖矿并且保证在路途中不得耗尽资源。游戏允许玩家挖矿获得收益,并利用初始资金及收益在村庄随时补给资源。玩家必须在截止日期之前抵达终点,并保留尽可能多的留存收益。该情景策略游戏将野外求生中多变的天气与不定的决策通过情景模拟的方式真实呈现,对于玩家的数据意识、信息搜集与灵活决策能力以及风险防控都提出了很高要求。本文将基于图论与马尔可夫决策有关模型,综合考虑玩家在两种情形下所面临的现实困境,并对该最优策略展开具体讨论。
二、问题分析与求解
(一)未来信息已知:基于多阶段决策的动态规划模型
经济学中,期望收益为根据已知信息对未来收益的预判。在游戏中,玩家期望在规定的时间内获得尽可能多的资金。由于天气数据与地图完全已知,本文首先根据地图信息建立图论模型,接着使用动态规划将沙漠掘金问题划分为多阶段决策模型,从基本逻辑出发,首先规划出掘金路线,进而分析资源购置策略,在此基础上依据天气状况与资源情况求解挖矿策略,最终通过筛选期望收益的最大值来求取玩家的最优策略。
1. 图论模型
设地图共有n个区域,其中含有k个村庄,记为集合A={a1、a2…ak};含有m座矿山,记为集合B={b1、b2…bm}。沙漠起始点记为s0,沙漠终点记为sn。w1(t)为第t日水资源基础消耗量,w2(t)为第t日食物资源基础消耗量。矿山的单日收益为r,每箱水资源的质量为m1,基准价格为p1,每箱食物资源的质量为m2,基准价格为p2。玩家在第t天的剩余水资源质量为M1(t)、剩余食物资源质量为M2(t)、剩余资金为C(t)。游戏时限为t0天,承重上限为Wmax。
玩家在任一区域可选择“停留”状态,其时间递归式如下:
在非沙暴天气时,玩家在任一区域可选择“移动”状态,其时间递归式如下:
玩家在矿山区域时,可以选择“挖矿”状态,其时间递归式如下:
玩家经过或停留村庄区域时,可以购置资源,购置资源产生的递归式如下:
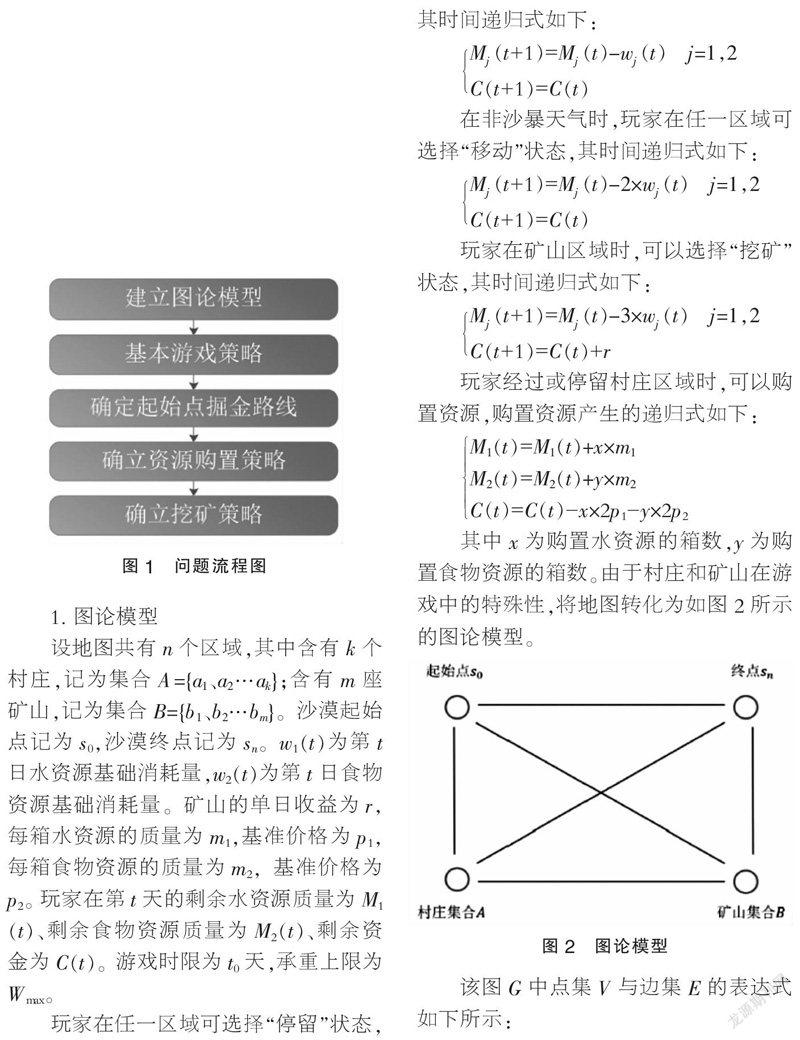
其中x为购置水资源的箱数,y为购置食物资源的箱数。由于村庄和矿山在游戏中的特殊性,将地图转化为如图2所示的图论模型。
该图G中点集V与边集E的表达式如下所示:
式中,si∈V。设第t天的玩家区域位置为St,可将原问题分解为不同区域集下的多阶段决策问题,通过求解每一阶段下的最优策略建立动态规划模型。
2. 基本游戏策略
为获取更多的资金,有两种基本途径:收益最大化与支出最小化。我们从这两个基本途径延伸出四条基本游戏策略:
满载原则:资源不足时玩家需要前往村庄补充必备资源,多次重复前往村庄将增加路途资源的消耗,为减少前往村庄次数,除最后一次购置资源外,其余应使负重满载。设第i次经过(或停留)村庄集合时购买的水资源为xi箱,食物资源为yi箱,应有:
不剩余原则:在终点剩余资源将以基准价格的一半退回,造成资金浪费,结合满载原则,最后一次购置资源的数量xn、yn应有如下关系:
3. 掘金路线策略
玩家在起始点面临三种选择:向村庄集合A出发购买必备资源;向矿山集合B出发来获取未来的资金收益;向终点sn出发以结束游戏。由此引申出三种掘金路线:
玩家在村庄补充资源后,若时间充裕将前往矿山采矿;玩家在矿山消耗大量资源后,若时间充裕将前往村庄补充资源。因此路线中村庄和矿山应交替出现,直至接近时限玩家向终点移动。则有:
由于游戏目标为在规定时限内获取更多的资金,从期望收益角度分析三种路线,期望收益高的路线为最优掘金路线,并通过顺路原则求解相应村庄和矿山位置。
4. 资源购置策略
在沙漠起始點可以低廉价格购买一次资源,在沙漠途中经过或停留村庄时均可购置资源,资源购置量应匹配于资源消耗量。此外,由于水资源和食物资源的价格不等,在村庄购买将进一步拉大两种资源的差价,在不改变掘金路线的情况下,在初始点应以低廉价格购买尽可能多的贵重资源。
(2)村庄资源购置策略。在上节已经求得三种掘金路线,设第i次经过(或停留)村庄集合B时购买的水资源为xi箱,食物资源为yi箱,据满载原则,xi与yi满足:
设最后一次经过村庄经过(或停留)村庄集合B时购买的水资源为xn箱,食物资源为yn箱,据不剩余原则有:
5. 挖矿策略
(1)前往终点决策。当剩余时间较少且资源不足时,玩家面临的选择为:前往村庄补给后返回矿山挖矿;直接前往终点,由此生成两种不同的决策方案。我们从期望收益角度分析两种方案,期望收益高的方案为最优决策。
(2)前往村庄时机。由于不同天气对路途的资源消耗不同,在给定所有天气数据的情况下可以选择合适的天气前往村庄购置资源。设fj和gj分别表示第次前往矿山挖矿,则前往村庄的最优决策为:
(3)暂停挖矿。由于在村庄购置资源价格为基础价格的二倍,在沙暴或高温天气挖矿将承担高额的资源费用,在时间期限允许的条件下,可以尝试选择在沙暴或高温天气暂停挖矿休息,本策略的触发条件为:
综上,从玩家状态分析,策略示意图如图3所示。
(二)未来信息未知:基于风险预测的多阶段马尔可夫决策模型
经济学中,风险预测或风险评估指对未来不确定性的量化计算和预测。玩家在游戏中通过目前的状态与当天的天气情况(环境状态),产生移动、停留挖矿等行为(对环境做出动作),并通过环境的反馈调整决策。由于玩家的目标仍为到终点时资金的最大化,本文利用概率论相关理论的对期望收益进行定量评估预测,进而做出最优决策。由于情景的相似性,我们沿用前问题的变量符号与游戏基本策略。
1. 马尔可夫决策模型
马尔可夫决策(MDP)的流程图如图4所示。
马尔可夫决策包含一组交互对象:智能体:MDP中进行机器学习的代理,可以感知外界环境的状态进行决策、对环境做出动作并通过环境的反馈调整决策。环境:mdp模型中智能体外部所有事物的集合,其状态会受智能体动作的影响而改变,且上述改变可以完全或部分地被智能体感知。
马尔可夫决策过程由五部分组成:{State,Action,Psa,γ,Reward},其中State表示状态集合,Action表示行动集合,Psa表示状态转移概率,γ表示阻尼系数,Reward表示该行动的回报。针对该游戏,State包含位置变量s(t)、所剩资金变量C(t)、所剩水资源变量M1(t)、所剩食物资源变量M2(t);Action有四种情况:“停留”、“移动”、“挖矿”、“购置资源”;阻尼系数γ在该问题中为1;Reward由资金时间递推式决定。最终的路线与资源购置方案仍由期望收益最大给出:
2. 风险预测模型
设晴朗、高温、沙暴天气的概率为h1~h3,其对应的水资源基础消耗量为w11~w13,食物资源基础消耗量为w21~w23。利用概率论,对不同行为的资源消耗与资金变化进行预测。
(1)停留。玩家在任意天气均可以选择“停留”,两种资源的变化期望为:
(2)移动。玩家在非沙暴天气可以选择“移动”。由于每次移动成功的概率为h1+h2,需要求解移动距离为l时的时间消耗。这是一个帕斯卡过程,据概率论,帕斯卡分布的分布函数如下:
因此,该过程的耗时与资源消耗期望如下:
考虑到天气的随机因素,需要多准备一些资源以应对极端情况(多次出现沙暴天气无法移动)。由于不同玩家有不同的游戏偏好,我们引入风险偏好系数k,多准备k·σ的资源(σ为标准差),两种资源消耗的期望更正为:
(3)挖矿。玩家在矿山区域可以选择“挖矿”,类比“停留”时的资源消耗,挖矿天的资源消耗与资金变化的期望为:
(4)资源购置。玩家经过或停留村庄区域时,可以购置资源,购置资源产生的递归式如下:
其中x为购置水资源的箱数,y为购置食物资源的箱数。
3. 基本游戏策略
与前问题相比,游戏规则除天气情况未知外完全一致,因此最短路原则、满载原则、顺路原则与不剩余原则仍然适用。针对未来天气的未知性,根据风险预测原理,我们期望决策具有较小的风险性,由此引申出第五条基本策略:同路原则。
4. 玩家策略
由于情景的相似性,我们仍沿用前问题模型中的掘金路线策略、资源购置策略与挖矿策略,并针对未来天气情况未知的条件进行改进。
(3)挖矿策略。挖矿策略依然包含三部分内容:前往终点决策;前往村庄时机;暂停挖矿,与前问题保持一致。特别是当满足下式时,启用暂停挖矿策略。
三、结论与推广
本文根据图论、博弈论的有关原理建立数学模型,对游戏玩家多阶段、多目标的最优策略展开探究。基于马尔科夫的决策模型是本文的一大特色,综合考虑到模型拥有的优化功能,可以考虑将其推广至现实生活中个人面对复杂情境时的决策與权衡,以及企业面临变幻莫测的市场环境时合理的应对之策等相关议题的探讨之中。(注:本文数据与资料来源:2020年全国大学生数学建模比赛B题)
参考文献:
[1]Brihaye T,Geeraerts G,Hallet M,et al.On the termination of dynamics in sequential games[J].Information and Computation, 2019,272:104505.
[2]Dhiman A,Uttam T,Balakrishnan S. Implementation of sequential game on quantum circuits[J].Quantum Information Processing,2020,19(04):1-16.
[3]陈如峰.自学习策略价值风险模型研究与应用[D].成都:电子科技大学,2020.
[4]王中玉,曾国辉,黄勃,方志军.改进A*算法的机器人全局最优路径规划[J]. 计算机应用,2019,39(09):2517-2522.
(作者单位:西安交通大学)
