MIMO中基于预处理的广义加权Gauss-Seide算法

史传胜,冯 姣

(南京信息工程大学 电子与信息工程学院，南京 210044)

0 引 言

在大规模多输入多输出(Multiple-Input Multiple-Output，MIMO)系统中，基站端有数百个天线来同时服务几十个用户，并且基站天线数量远高于用户天线数量[1]。最大似然估计(Maximum Likelihood，ML)虽然检测性能最佳，但计算复杂度很高，在实际系统中很难得到应用[2]。因此学者们在降低检测性能的前提下提出了低复杂度的近似线性最佳检测算法，如迫零(Zero Forcing，ZF)算法和最小均方误差(Minimum Mean Square Error，MMSE)检测算法[3]。MMSE和ZF算法涉及到矩阵的求逆问题，当用户数量很多时，这些检测器的计算复杂度会很高。基于此，出现了简化算法，如共轭梯度[4](Conjugate Gradient，CG)、高斯-赛德尔(Gauss-Seide，GS)[5]、雅克比[6](Jacobi，JA)和超松弛迭代[7](Successsive Over-Relaxation，SOR)算法。文献[8]提出了基于邻域搜索的似然上升搜索(Likelihood Ascend Search，LAS)检测算法，通过利用邻域搜索算法来选择初始向量，给出了一个接近最优的解；文献[9]提出了一种基于JA迭代算法的GS(Joint Jacobi and Gauss-Seidel，JA-GS)算法，JA-GS算法主要利用JA和GS迭代算法进行信号检测，虽然性能较好，但其收敛速度偏慢，复杂度偏高。

为解决这一问题，本文提出了一种基于预处理的广义加权GS(Generalized Weighted-Preconditioned Gauss-Seide，GW-PGS)检测算法。该算法通过对迭代矩阵进行预处理，并且提出自适应的加权因子方案，进一步提高了算法的检测性能和收敛速度。仿真结果表明，在128个基站天线和16个用户天线数的前提下，与传统GS检测算法相比，GW-PGS算法的误码率(Bit Error Rate，BER)性能更优。

1 大规模MIMO系统模型

在上行链路大规模MIMO系统中，假设每个用户配备一个天线，M为基站天线数，N为用户数[10]，一般情况下M≫N，例如M=128和N=16。大规模MIMO系统模型如图1所示。图中，发射端信号xN经过用户天线N向基站天线传输，基站端天线M接收到的信号经过解调后得到yM。

图1 大规模MIMO系统模型

基站接收到的上行信号为

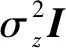
为避免复数运算，将模型转换为

式中，z为噪声。

2 传统信号检测算法

2.1 MMSE检测算法

在上行大规模MIMO系统中，MMSE检测算法检测性能比较优异，即通过较为简单的线性操作即可将原始发送信号x从接收端接收信号y中恢复出来。为了恢复发送的信号，使用加权滤波矩阵WMMSE来实现信道的逆转。线性MMSE算法中发送信号的接收估计值WMMSE为

式中：HH为H的对称转置矩阵；yMF=HHy为匹配滤波器输出。算法的复杂度主要体现在矩阵的求逆方面。因此在实际的大规模MIMO系统中， MMSE系统线性检测算法增加了硬件实现难度，也限制了该算法在实际中的应用。大部分大规模MIMO系统低复杂度检测算法的原理就是通过降低求矩阵的逆的复杂度来降低MMSE整体算法的复杂度。

2.2 GS检测算法

在大规模MIMO系统中，当基站天线数远远大于用户数时，信道之间逐渐趋于正交[10]，MMSE滤波矩阵为对称正定矩阵，且对角占优。因此，可将A分解为

在GS检测算法中，信号可以估计为[11]

式中，D、L和U分别为A的对角矩阵、严格下三角矩阵和严格上三角矩阵。

3 GW-PGS迭代算法

3.1 初始值和加权因子的选取

定义1 带状矩阵表示在矩阵A中，所有的非零元素都集中在以主对角线为中心上下w元素的带状区域中。其中w小于矩阵的维度。

由A=HHH+σ2I可知，A是一个N×N的方阵，那么带状矩阵Dw可以写成：

式中，Ai,j为A中的元素。当w=1时，有

那么初始解x0可以写成：

为了更好地适应不同的天线配置，本文提出了一个自适应的加权因子μ。然而直接推导该最优因子比较复杂，所以本文采用系统仿真的方式选取次优的加权因子。

3.2 GW-PGS迭代算法

GW-PGS迭代算法是一种求解大型线性方程组的稳定迭代方法。GW-PGS迭代算法能够快速求解yMF=Ax的大型方程组。其中系数矩阵A为一个正定Hermit矩阵。将式(6)写成两个半迭代方程，可以得到收敛速度更快的GW-PGS迭代算法。

用GW-PGS迭代算法进行第1次半迭代，k为迭代次数：

使用GW-PGS迭代算法进行第2次半迭代：

将两次迭代的结果通过加权因子μ结合在一起：

当μ取1时可以发现，GW-PGS迭代算法退化成了传统的GS迭代算法。为了加快GW-PGS迭代算法的检测速度，本文提出了预处理的方案，在线性方程组yMF=Ax前加入一个静态迭代预调节器。将yMF=Ax写成Q-1yMF=Q-1Ax形式，式中，Q为非奇异、对称和正定矩阵。迭代预调节器应该近似A-1,使得‖I-Q-1A‖<1[13]。

在本文中，采用了JA预调节器，设Q=diagonal(A)，diagonal()为求主对角矩阵函数。对角矩阵的预处理操作在计算上是高效的，并且降低了GW-PGS迭代算法的整体复杂性。

综上所述，本文所提GW-PGS迭代算法的流程如下，tril()和triu()分别为下三角和上三角函数。

算法1 ：GW-PGS迭代算法：

输入：y，H，σ2，

预处理：

1:A=HHH+σ2I，

2:yMF=HHy，

3:Q=diagonal(A)，

7:D1=triu(D_,-1)，

8:x0=D-1yMF，

9：提出自适应加权因子μ，

10:迭代：

fork=1 tondo

End for

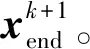
4 复杂度分析

本文主要分析了GW-PGS迭代算法的复杂度和一些线性检测算法的复杂度，并做了一些比较。相比而言，乘法运算的计算复杂度远比加法高[14]，所以算法的复杂度通常是比较乘法运算的次数和相同迭代次数时需要做的乘法次数。表1所示为对GW-PGS、传统的理查德森(Richardson,RI)、JA、GS和MMSE算法计算复杂度的比较。

表1 不同检测方法计算的复杂度

5 性能仿真

为评估算法性能，本文在Matlab软件上仿真了所提算法和现有算法的BER—信噪比(Signal Noise Rate，SNR)曲线。分析了所提GW-PGS迭代算法的检测性能并与传统的GS算法以及MMSE算法的检测性能作了对比。设置仿真时的传输信道为不相关瑞利衰落信道，基带信号调制方式为二进制相移键控( Binary Phase Shift Keying，BPSK)、四相相移键控(Quadrature Phase Shift Keying，QPSK)、16正交幅度调制(16Quadrature Amplitude Modulation，16QAM)和64QAM，天线规模为128×16、128×32、16×16、32×16和64×16。模拟参数如表2所示。

表2 模拟参数

表3所示为SNR=16 dB，天线数量为128×16时，不同算法每比特实乘运算次数的对比。由表可知，MMSE算法的每比特实乘次数最高，其次是GW-PGS、GS、JA和RI算法。表4所示为SNR=16 dB，基站天线数为128时，GW-PGS算法在不同用户天线数下每比特实乘次数的对比。由表可知，在基站天线数量不变的前提下，随着用户数量不断增加，GW-PGS迭代算法的复杂度不断升高。

表3 SNR=16 dB，天线数量为128×16时，不同算法每比特实乘次数

表4 SNR=16 dB，基站天线数为128时，GW-PGS迭代算法在不同用户天线数下的每比特实乘次数

图2所示为SNR=16 dB，收发天线为128×16时，不同加权因子μ下GW-PGS迭代算法BER性能仿真图。选取的μ以0.2为步长进行仿真。经过多次实验仿真发现，μ∈(-1.7,1.1)时有较为优异的BER性能。由图可知，当μ=-0.1时，GW-PGS迭代算法的检测性能最佳。当μ选取不当时，会导致GW-PGS迭代算法的检测性能变差。

图2 SNR=16 dB，收发天线为128×16时，不同μ下GW-PGS迭代算法BER性能仿真图

图3所示为大规模MIMO系统规模为64×16，在64QAM调制下，GW-PGS迭代算法与MMSE、Jacobi和GS算法的检测性能比较。仿真结果表明，GW-PGS迭代算法随着迭代次数的增加，算法的检测性能也在不断提高。以GS算法BER曲线作为对比参照，由图可知，迭代次数为1时，GW-PGS迭代算法的性能与GS算法的性能相比，传统GS算法性能更优。当迭代2次时，本文所提GW-PGS迭代算法的检测性能和传统GS和JA算法检测性能相比有明显的优势，在BER=10-3时，相比于GS算法，SNR有0.8 dB的增益。迭代3次时，GW-PGS迭代算法相比于GS算法，SNR有1.6 dB的增益，与JA算法相比，其优势更明显。

图3 收发天线为64×16且使用64QAM调制时，几种算法的BER性能比较

图4所示为本文所提GW-PGS迭代算法与RI、JA、GS和MMSE算法的计算复杂度比较。由图可知，算法复杂度最低的是RI算法，其次是JA、GS、GW-PGS和MMSE算法。为了平衡检测性能与计算复杂度之间的矛盾，本文所提GW-PGS迭代算法的复杂度要比传统的JA和GS算法复杂度稍微高一点。复杂度最高的是MMSE算法，这是因为MMSE算法涉及到了矩阵的求逆。

图4 天线数量与算法计算复杂度的关系

图5所示为在不同基站天线数、16个用户天线数和64QAM调制方式下，所提GW-PGS迭代算法检测性能比较。大规模MIMO系统中，在用户天线数量不变的前提下，随着基站天线数量的增加，GW-PGS迭代算法的检测性能也随之提高。当SNR=16 dB时，天线配置为128×16的BER达到10-5量级，相比之下，SNR=16 dB时，天线配置为64×16的BER只有10-3量级，天线配置为32×16的BER只有10-2量级，天线配置为16×16的BER只有10-1量级。由于基站天线数量变多，空间自由度也随之提高，并且提高了信号的传输效率和系统容量。因此在16个用户天线数量下，随着基站天线数量的增加，GW-PGS迭代算法的检测性能也随之提高。

图5 不同基站天线数、16个用户和64QAM调制方式下，GW-PGS迭代算法的BER性能比较

图6所示为在128个基站天线和16个用户的配置下，不同调制方式对GW-PGS迭代算法BER检测性能的影响。仿真结果表明，该算法在BPSK调制下性能表现更优异，其他性能表现依次为QPSK、16QAM和64QAM。在抗加性高斯白噪声方面，BPSK性能最好。由于64QAM调制方法的判决取样点比BPSK、QPSK和16QAM都要多，所以增大了其BER，导致其性能最差。

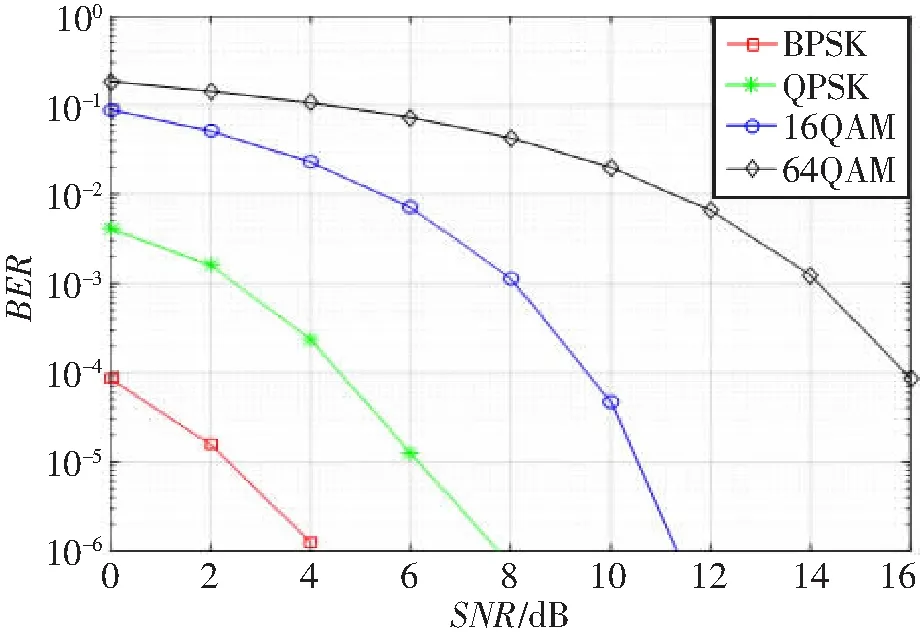
图6 收发天线为128×16时，在不同调制方式下的GW-PGS迭代算法BER性能比较

6 结束语

本文提出了一种新的大规模MIMO系统上行链路用户信号检测算法。为了提高算法的性能，本文提出了一种GW-PGS迭代算法。在该算法中，首先提出了基于预处理的初始化方案，在不增加额外复杂度的情况下加快了收敛速度；其次，为了更好地适应不同的天线配置，本文提出一个自适应的加权因子μ。仿真结果表明，本文所提方法获得了较优的BER性能，与传统的大规模MIMO系统检测算法相比有明显的优势。