带有深度学习的多特征选择组合算法燃气轮机参数建模

张宝凯

(中国大唐集团科学技术研究总院有限公司华东电力试验研究院，合肥 230031)

煤炭发电以低廉的经济成本占据着我国能源结构的主要部分，发电过程中释放的NOx污染物危害自然社会系统。与煤炭发电相比，燃气-蒸汽联合循环电厂以天然气为燃料，发电产物清洁，NOx排放浓度仅为煤炭电厂的1/10[1]。

燃气轮机NOx排放浓度能够间接反映机组的燃烧健康水平，是建立燃烧调整模型的重要变量[2]。异常的排放特性影响机组的燃烧效率，使燃烧脉动不稳定，触发负荷超驰机制。准确地预测NOx可以对异常工况进行预警，消除安全隐患。

构造预测模型的第一个关键步骤是针对研究问题找到适合的建模方法。在已有研究中，建模方法以机理方法[3]、统计学方法[4]和数据驱动的智能方法[5]为主要三类。赵雄飞等[6]结合统计学方法得到了燃气轮机数学建模特性方程最佳拟合次数，确定了拟合曲线，减小了与对象实际曲线运动规律间的建模误差。曹军等[7]利用APROS软件对燃气轮机热力过程进行质量、动量分析，遵循能量守恒法则对F级燃气-蒸汽联合循环机组全范围过程进行实时动态仿真。然而，以上方法在建模精度方面都有提升空间。厂级数据监控系统(supervisory information system，SIS)作为智慧电厂建设平台实现了过程控制中大量参数数据状态的监测记录与实时访问，为数据驱动智能建模控制策略提供了技术支持[8]。李景轩等[9]设计了一种以智能算法作为机理模型误差补偿的混合模型控制器方法，并对不同组合方式的设计进行了基于分布式控制系统(distributed control system，DCS)数据的验证实验，提高预测精度。liu等[10]将基于正交试验的模糊优化方法应用于传感器建模过程中，提高了传感器建模效率与传感器精度。以上研究在参数建模方面取得了成功，然而均为浅层机器学习方法，不能够捕捉数据底层的深层次有用信息且建模精度有提升空间。

构造预测模型的另一关键步骤是找出更能解释内生变量非线性逻辑关系的代表性解释变量。燃气轮机变量建模过程中极强的关联性增加了模型的学习时间，产生的共线性问题也会使模型精度不高。与之相反，缺失变量则会泛化模型的解释性。因此，通过对解释变量进行特征约简，剔除与内生变量不相关、弱关联以及冗余的建模解释变量可以整体改进预测模型的鲁棒性、精度及学习速度。Zhang等[11]基于偏互信息(partial mutual information,PMI)算法解决了解释变量间的关联关系对建模精度的影响，在选择出的最佳输入量集的基础上构建有效高精度预测模型。该方法在极短时间内，凭借对自身数据的度量规则处理大量高维维数下的无关特征，且算法在进行选择特征时独立于后续学习器，计算效率大大增强。Zhang等[12]针对LASSO算法在变量选择时没有将协变量之间的相互作用考虑在内，设计出一种利用特征超图与多维互动信息技术相融合的新正则化项，通过约束有效评估特征特性。吴笑研等[13]对煤电锅炉效率相关生产数据进行CART分析，选择出重要性高于5%的动态建模特征，满足了锅炉燃烧控制生产运行需求精度的要求。二种嵌入式方法在特征选择时可认为是将算法与学习器一同作为优化整体，参与学习训练过程，挖掘了数据结构中的内在相关性，检测数据冗余。以上研究在特征选择方面效果表现突出，凭借自身算法特性均能实现对变量特征的选取。

与已有研究构建模型时输入特征采用单一、分步特征选择[14]方法的浅层机器学习机模型不同，本文设计了一种基于深度置信网络非线性组合多特征选择方法，具体工作在于三个方面：(1)结合专家机理分析CART、PMI、LASSO算法，对NOx预测模型的输入参数进行选取；(2)采用深度DBN网络对建模参数进行建模；(3)采用DNN算法对不同特征选择下的预测模型进行非线性组合，得到最终MFNDBN预测模型，并且设计实验验证所提出算法的有效性。

1 联合循环系统分析

燃气-蒸汽联合循环系统主要由燃气轮机、余热锅炉以及汽轮机间相互协调，快速响应电网AGC控制，并且由于占地体积小、机组启停快、发电效率高以及CO2、SO2、NOx排放量少而逐渐被关注。工作状态下，空气经前置过滤器后由进口导叶IGV进入压气机形成压缩的高压空气，并通过进气加热模块IBH将空气的预混燃烧范围进一步扩大。天然气通过前置站模块将品质合格的天然气经速比阀、燃料阀后以环管分布的喷嘴送入燃烧室与高压空气混合燃烧，膨胀的高压高温燃气带动透平叶轮经负荷齿轮箱将机械能传递给发电机，而尾端的高温燃气继续进入余热锅炉，通过辐射换热，将给水加热至指标合格的工质驱动汽轮机缸体内动叶片，带动发电机发电。图1经燃烧室燃烧后的燃气中含有的NOx浓度间接反映了机组其他关联参数的运行状态是否在合理的设计值范围内，NOx参数建模为机组燃烧稳定与安全设计下的其他关键参数优化提供决策指导。

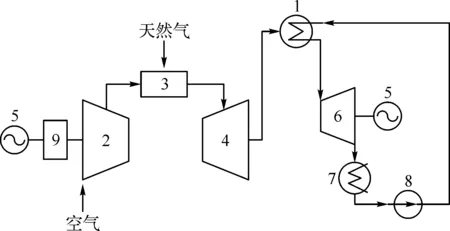
1—余热锅炉；2—压气机；3—燃烧室；4—透平；5—发电机；6—汽轮机；7—凝汽器；8—凝结水泵；9—负荷齿轮箱。图1 燃气-蒸汽联合循环系统流程简图

2 基于深度置信网络的多特征选择算法NOx排放建模

2.1 数据预处理

离群点是一种在数据挖掘过程中偏离正常监测下的数据数值，它的产生均由突发事件下的内部机制变化、测量等错误行为而引发，会对模型预测增加难度。DBSCAN异常点检测方法是一种可以利用数据特征分布密度程度不同而检测离群点的高效聚类算法[15]，它不需要对簇的数量进行提前指定，而是通过密度来确定相似属性簇。其中，算法将所有样本点划分为核心点、边界点以及不同于前二者的异常点，核心点和边界点被划分在同一个簇中，而后者则在簇中心ε-领域(Epsilon)内。ε-领域计算如式(1)和式(2)所示：

Nε(Xj)={Xi∈D|dist(Xi,Xj)≤ε}

(1)

(2)

式中:dist(Xi,Xj)定义为马氏距离；D∈{X1,X2,…,Xn}；ε为小的正数；Nε(Xj)代表与个体Xj距离不超过小正数的所有个体集合，也称ε-领域。

系统时滞特性造成稳态工况下参量调整的目标值与现场实际反馈测定值存在较大延时，时间响应与超调量的关系很难衡量而产生随机信号。这种信号普遍存在于测量中，因此需要信号进行基于最小二乘原理的Savitzky-Golay(S-G)平滑滤波处理，并保存原始信号的形状和宽度，以此得到真实数据状态，计算公式如式(3)所示：

(3)

式中:Xj′为滤波后数据；Xj+1为原始测量数据；ci为滤波系数；N为滑动窗口数据个数2m+1；m为窗口宽度。

以天然气温度为例计算异常值剔除与平滑滤波前后信号变化情况，如图2所示。其中上图表示原始数据，下图表示预处理后的数据。

图2 预处理前后数据对比结果

建模所需31个变量为：燃气轮机负荷(DW)、压气机排气压力(Cp)、IGV角度(Cs)、气体燃料进气压力(Fpg1)、气体燃料阀间压力(Fpg2)、气体燃料温度(Ftg)、燃烧脉动F1～F18、压气机入口温度(tti)、压气机排气温度(ttd)、压气机压比(Cr)、环境温度(tati)、排气温度(txxtm)、天然气流量(Fqg)、NOx浓度(Ppm)。将所列变量进行数据量化至[0,1]区间，去除单位限制，须要说明的是在一段时间内由于燃料流量一直保持不变，所以在建模时，将该变量剔除。

2.2 输入变量特征选择

偏互信息是在互信息(mutual information，MI)基础上改进而来的特征选择方法，它通过消除已选输入集下待选变量的条件期望值，剔除已选变量集影响的待选变量的残差，以此消除因子间的相关性对互信息的影响。定义xi为输入因子，z为已选输入因子集，yi为输出因子，xi与z之间存在耦合关联，则xi与yi之间的偏互信息计算公式如(4)至(6)所示：

(4)

xi′=xi-f(xi|z)

(5)

yi′=yi-f(yi|z)

(6)

式中:xi、yi之间的偏互信息用V(xi,yi)表示；f为条件期望函数；xi′、yi′分别为剔除因子z影响之后的残差，通过赤池信息准则Taic值作为衡量模型复杂度和模型拟合泛化性能的收敛终止条件，当值随着变量个数增加而不断减少达到最低点时，筛选出的变量集为最优集合。定义公式如(7)所示：

(7)

式中:ei为已选因子集z的回归残差；p为已选变量个数。

决策树CART以基尼系数Ggini为指标,根据分类后子集Ggini最低为最优分类规则，设计评价函数。计算现有样本对原始数据样本集合H的Ggini系数，如式(8)所示：

(8)

式中:pj为数据集中各类别概率；k为样本类别。

然后计算相应属性划分后的Ggini系数，计算公式如式(9)所示：

(9)

式中:H1、H2为样本划分的二个子集，基于Ggini原则找到最小Ggini系数对应的切分特征。

LASSO回归算法对变量特征进行选择的主要思想是基于参数正则化，通过对系数增加惩罚函数的约束条件，而实现某些回归系数趋于0的稀疏压缩，达到“变量选择”的目的。一般情况下，LASSO回归算法采用L1范数惩罚，与L2范数相比，特征选择更严格，更能使回归系数严格接近于0，同时避免模型过拟合。其目标函数定义如公式(10)所示：

(10)

式中:β∈Rp×1为回归系数向量；X∈Rn×p为特征矩阵；y为目标变量；λ为惩罚因子；‖‖为L1-惩罚项。

分别用3种特征选择算法(PMI、CART、LASSO)对建模输入特征进行特征选择并得到重要性排序结果。实验所得重要性排序由大到小的前5个变量的结果为偏互信息PMI：ttd、Fpg1、txxtm、tati、tti；套索回归LASSO：txxtm、tati、Cs、F17、DW；决策树CART：txxtm、tati、ttd、Cs、Fpg1。从排序结果可以看出，采用不同的特征选择方法对输入特征进行相关重要性分析得到的结果并不相同。

2.3 深度置信网络

典型的深度置信网络(deep belief network，DBN)由多个叠加的受限玻尔兹曼机构成的底层无监督网络和上层有监督反向网络组成。受限玻尔兹曼机(restricted boltzmann machine,RBM)的可见层v与隐含层h之间权重全连接，同层无连接，训练时，前一个RBM输出作为下一RBM输入并完成前一层RBM参数θ的粗调，直至训练到网络顶层，之后通过顶层逻辑回归网络进行误差反向传播的参数细调优化，同时顶层网络接受最后一个RBM的特征输出，完成网络预测。图3为顶层网络为BP与4个RBM底层网络构成的DBN拓扑结构。

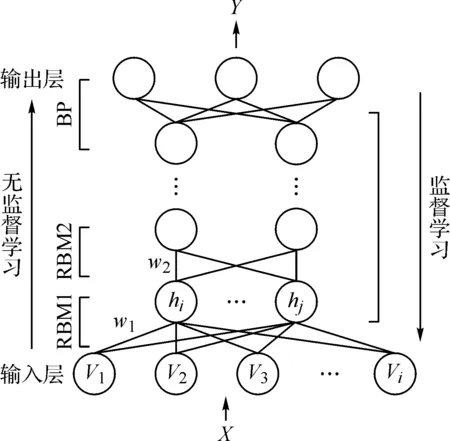
图3 深度置信网络结构

其中，单个RBM的能量函数如公式(11)所示：

(11)

式中:ai、bj分别是可见层vi与隐层hj的偏置；wij为可见层vi与隐层hj的连接权重；θ={wij,ai,bj}。由公式(11)可得vi与hj的联合概率分布如公式(12)所示：

(12)

(13)

式中:Z为—归一化因子；f为条件期望函数。公式(14)与公式(15)为独立的vi与hj节点的激活概率：

(14)

(15)

(16)

式中:σ为sigmoid激活函数。

wij、ai、bj更新规则可按照公式(17)～(19)进行更新[16]：

wij=wij+η(fdata(vihj)-frecon(vihj))

(17)

ai=ai+η(fdata(vi)-frecon(vi))

(18)

bj=bj+η(fdata(hj)-frecon(hj))

(19)

式中:η为学习率;fdata为训练样本期望;frecon为模型定义期望。本文中η为0.09，frecon为0.06，隐层结构为4层，输入特征Xi个数为i=10，分别为各自特征选择算法选择后的变量，输出Y为燃气轮机NOx排放浓度。

2.4 基于深度学习的多特征选择组合预测算法

单一的特征选择算法根据自身的评价标准来对表现出不同特征属性的特征进行选择，选取的建模输入最佳子集有所区别，并且单一的特征选择方法由于算法的局限性所得到的模型精度也是有限的。本文以PMI、CART、LASSO特征选择算法对同一预测问题进行建模的结果分析，提出了一种MFNDBN方法。算法流程如图4所示，实施步骤如下。

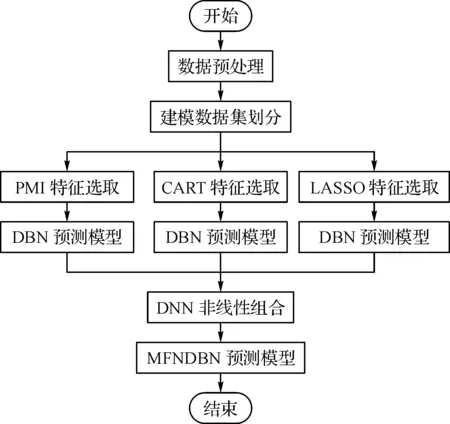
图4 建模流程图

步骤1：基础建模模型。将原始样本数据经过数据预处理后分别用PMI、CART、LASSO进行特征选择并划分模型预测的训练、测试集、验证集Pj={xi,y},i=1,…,N，j=1,2,3。将PMI、CART、LASSO算法下得到的特征重要性评分由大至小的顺序进行标签排序，结合实验法与专家知识选取各自特征选择算法前10个特征作为DBN建模输入X，输出特征为NOx，然后通过训练集分别进行DBN建模训练。

步骤2：非线性组合。根据步骤1训练的模型得到PMI、CART、LASSO预测模型的测试集与验证集预测值。假设3种特征选择建模训练模型为fp、fc、fl，则第g个样本的预测值结果分别为y1、y2、y3，将3个模型验证集和测试集的预测结果重新划分新的数据集。最后，采用DNN算法将fp、fc、fl模型进行非线性组合，得到最终更精确的MFNDBN预测模型，具体公式如下：

y1=fp(Xp,w1,b1)

(20)

y2=fc(Xc,w2,b2)

(21)

y3=fl(Xl,w3,b3)

(22)

yg=f(y1,y2,y3,w,b)

(23)

式中:yg为以非线性组合方式得到的最终MFNDBN模型NOx排放预测值；Xp、Xc、Xl分别为PMI、CART、LASSO算法选择的前10个输入特征；w、b为模型权值与偏置，更新规则如公式(17)～(19)。

3 实验结果与分析

本研究数据来自某燃气-蒸汽联合循环电厂燃气轮机TCS数据采集系统，采集了2021年1月15日 17:12至 21:23时间段内与NOx排放浓度相关的参数特征30个，采样频率为1 min，共252组样本，表1给出了建模实验数据信息。

表1 实验数据信息

3.1 评价指标

为了比较验证各算法的性能，将平均绝对误差(Mmae)、平均相对误差(Mmape)、均方根误差(Mrmse)、相关系数(R2)4个评价指标作为标准，具体公式如(24)～(27)所示。

(24)

(25)

(26)

(27)

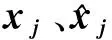
3.2 结果分析

3.2.1 DBN建模预测效果分析

图5为采用相同LASSO特征选择算法下不同建模模型(DBN、BP、SVR)的NOx排放预测结果的相对误差箱型图。其中，对比建模模型分别为BP算法与SVR算法。从线型图可以明显看出，深度网络DBN的预测能力比其他传统浅层机器学习算法BP与SVR更好，预测值相对误差上下四分位数更接近0附近。

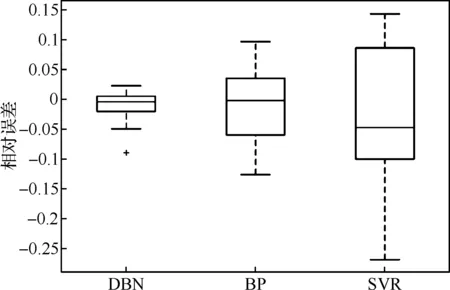
图5 不同建模模型预测结果

3.2.2 组合特性选择建模预测效果分析

为了验证MFNDBN方法性能，与PMI、CART、LASSO三种特征选择算法进行比较，为不失一般性，均采样DBN作为建模模型。图6为各方法在验证集下的预测值折线图。

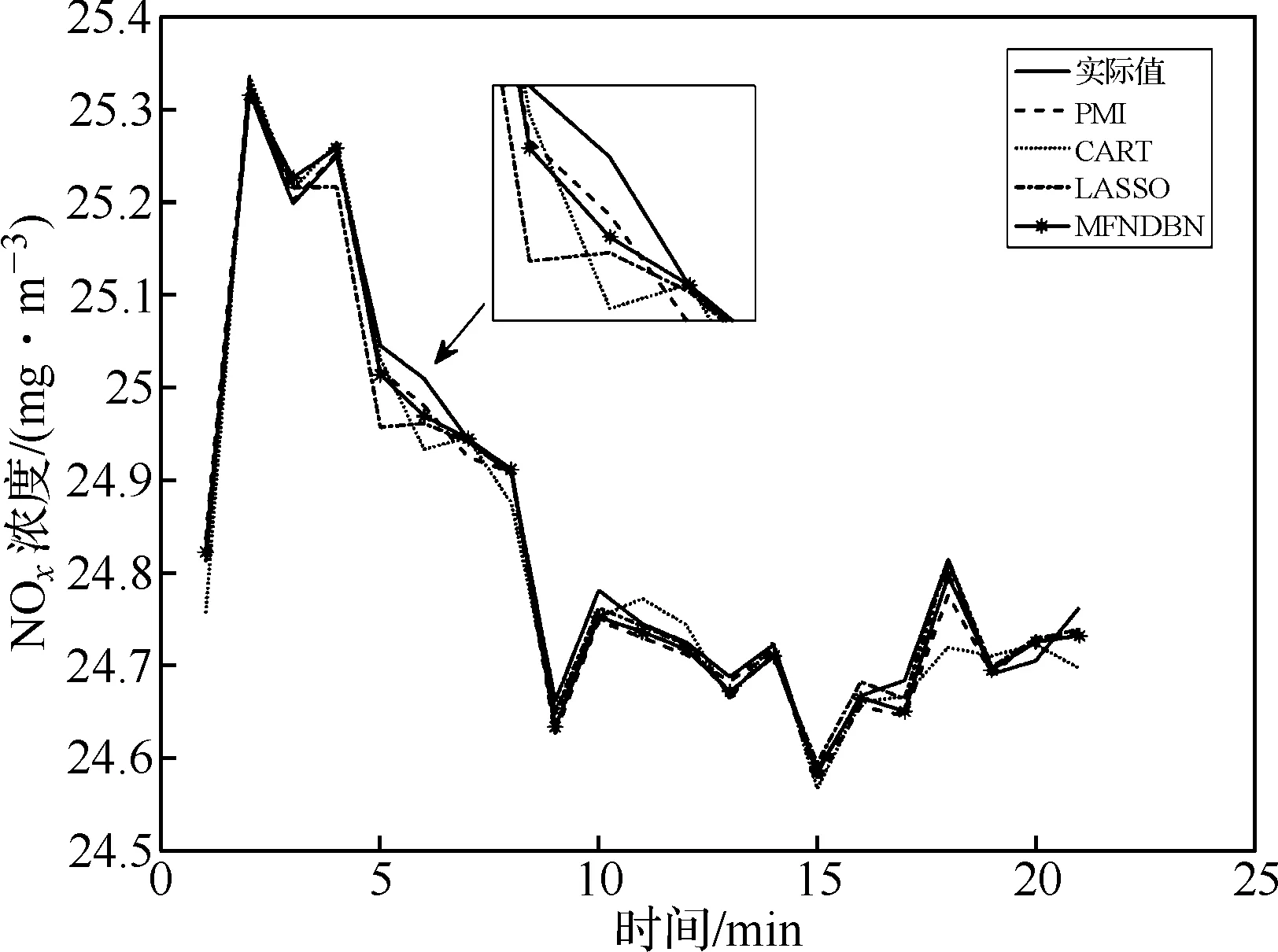
图6 不同算法预测结果

从图中可以看出三种特征选择算法与经过非线性组合预测的特性选择算法均对实际NOx排放有很高的预测能力，但组合方法更能真实反映排放量的变化趋势。表2为各算法评价指标对比。

从表2可以看出MFNDBN算法的三种指标值均比其他算法有所提高，采用MFNDBN算法比次优的PMI算法的Mmape、Mrmse、Mmae精度分别提高了10%、4.76%、11.76%，拟合效果R2提高了0.1%，说明MFNDBN算法达到了提高特征选择精度的要求，算法适用。

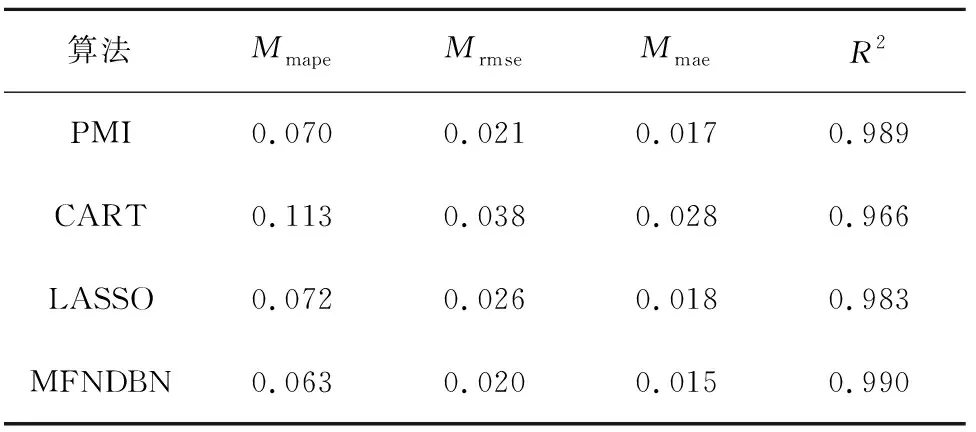
表2 不同算法评价指标结果

图7中(a)、(b)、(c)、(d)表示的是3种特征选择算法与MFNDBN方法对比的NOx排放预测值拟合实际测量值的散点图对比。其中黑色星号代表拟合分布；黑色实对角线为理想分布线；R2代表测量值拟合预测值的程度，值越大，模型预测精度越高。

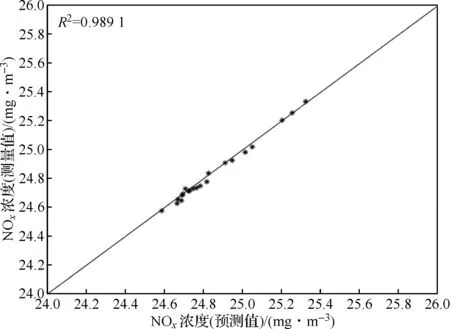
(a) PMI预测结果

从图7可以看出图7(d)的R2值最大并且预测值均匀地集中在理想曲线附近，实验结果说明所提算法能提高模型的预测精度。

4 结论

燃气-蒸汽联合循环机组的燃烧过程是复杂的物理过程，而燃气轮机NOx排放浓度能够反映燃气轮机的燃烧健康水平，是建立燃烧调整模型的重要变量，NOx浓度作为燃气轮机运行的一个状态参数耦合其他多参数，导致建立的模型很难实现准确的预测。针对这一问题，提出了一种基于PMI、CART、LASSO算法的多特征组合选择算法。实验从数据预处理、特征选取以及建模模型方面进行研究，基于燃气轮机TCS生产数据建模结果分析，所提出的组合特征选择算法能够提高单一特征选择下的建模模型预测精度。