跨声速风洞试验模型主动减振结构优化设计

曾开春,寇西平,2,*,杨兴华,余立,查俊

1.中国空气动力研究与发展中心 高速空气动力研究所,绵阳 621000

2.西北工业大学 航空学院,西安 710072

随着航空技术的发展,现代高性能飞行器研制对风洞试验数据质量的要求越来越高。然而,在高速风洞试验,特别是跨声速风洞试验中,经常会出现飞行器模型及其支撑结构大幅度振动的现象,不仅给试验数据质量带来影响,还会限制试验状态范围,甚至严重威胁试验模型和风洞的安全。由于气流激励载荷大、主动减振结构中作动器安装空间小等原因,高速风洞试验模型振动一直是国内外风洞运行部门广泛关注但难以解决的问题。

随着小体积、大推力压电陶瓷作动器技术的逐渐成熟,形成了一条解决风洞模型振动问题的有效途径,即在不改变支撑结构形式和外形的基础上,通过在支杆内集成压电陶瓷叠堆作动器(下文简称压电作动器),形成主动减振系统,利用压电作动器在电压激励下产生控制力,来达到抑制模型振动的目的。影响这类主动减振系统控制效果的主要因素是主动减振结构(下文简称减振结构)的控制能力和控制算法。目前,国内外已针对减振控制算法开展了大量研究,建立了较为有效的控制系统设计方法,但对减振结构的研究还相对较少。然而,在实际工程应用中,由于主动减振系统使用的压电作动器虽然推力大,但行程非常短(μm 量级),若安装压电作动器的结构设计不合理,将会导致主动减振系统难以获得良好的减振控制效果。因此,有必要对模型主动减振系统的结构进行设计优化研究,探索提升减振系统控制能力的有效途径。

欧洲的ETW(European Transonic Windtunnel)自20世纪90年代就进行了风洞模型主动减振技术研究。2001 年,ETW 和德国ERAS公司合作,研制了一套位于支杆与天平之间的主动减振系统。其将14个压电作动器环状布置在减振接头中,并通过14个预紧螺栓来实现对压电作动器的预紧。该方案能够对试验模型除滚转外的5 个刚体自由度振动进行控制,但是其在风洞模型振动最严重的模态,即纵向第一阶模态上,控制效果还难以满足使用需求。为此,2003年,ETW 又在支杆后端研制了一套纵向减振系统,与第一套减振系统配合使用,大幅度提升了对纵向一阶模态振动的抑制能力,但是其却并未公布该后端主动减振结构的技术细节。

美国 NASA (National Aeronautics and Space Administration)兰利中心在2007 年也开始和ViGYAN 公司合作,进行基于压电作动器的风洞模型主动减振研究。ViGYAN 公司的Balakrishna等首先在低速风洞中研制了一套位于支杆前端的验证性减振系统,证明了压电作动器用于风洞模型主动振动控制的可行性。随后,Balakrishna等根据该方案,以Pathfinder-I飞机模型支撑结构为对象,研制了一套支杆前端主动减振结构,该结构的4个压电作动器沿周向均匀分布,嵌入支杆内；为了提高减振系统的减振能力,还对压电作动器的周向布置方式进行了对比研究,给出了作动器的最佳布局及控制策略。在NTF(National Transonic Facility)风洞的试验结果表明,该减振系统能够拓展试验包线,但其减振能力还不足以控制迎角较大时发生的剧烈振动,仅可以提高这类振动的发生迎角。2011年,Balakrishna等又对风洞模型支撑结构动力学特性及压电作动器的耗能能力进行了建模分析,并在此基础上设计了一套位于支杆后端的减振结构。在NTF风洞和Ames-11英尺风洞的试验验证结果表明,该结构对模型振动有较强的控制能力,并可以大幅度提高模型剧烈振动现象的发生迎角。同时,Balakrishna等还指出,非定常气动载荷引起的模型支撑结构振动能量大,减振结构设计时需要尽可能地提高压电减振结构的能量耗散能力。

近年来,国内高校和相关研究机构也开展了风洞模型振动主动控制研究。陈卫东等首先使用内置于模型内的电磁式作动器来对模型振动进行主动控制。Liu等采用压电作动器,发展了一套位于支杆后端的风洞模型主动减振系统,其作动器布置方式与NTF前端减振结构布置方式相似,压电作动器通过预紧结构直接嵌入支杆根部。余立和Shen等发展了一种位于支杆后端,专门控制模型纵向振动的主动减振结构。该结构的压电作动器全部布置在支杆下方,并在结构前端设计2 个弹性铰链,以削弱结构对压电作动器的约束刚度,提高系统的振动控制能力。

上述研究中,对风洞模型主动减振结构的研究主要集中在压电作动器的布置、减振结构的形式等结构方案方面,缺乏对减振结构能力评价及优化方法的研究。然而,由于风洞试验对支杆外形尺寸有严格限制,无法简单地通过增加压电作动器的数量来提升主动减振结构的减振能力。这种情况下,对安装压电作动器的减振结构进行整体优化,就成为一条提升减振结构能力最有效的途径。因此,发展主动减振结构定量评价方法和结构优化方法,为主动减振结构方案选取及结构参数设计提供手段,对风洞模型主动减振系统研制具有重要意义。

本文针对基于压电作动器的风洞试验模型主动减振装置,研究其结构设计需要考虑的约束条件和减振能力指标度量方法,进而给出结构优化设计问题的数学表达和优化算法,以期探索出提升减振系统能力的有效途径。

1 风洞模型主动减振系统与原理

典型高速风洞模型支撑结构由模型、天平、支杆、直接头及弯刀机构依次连接组成,如图1所示(由于天平位于模型内腔,为了便于展示,图中将模型剖开)。为了减小气动干扰,支杆通常设计得较为细长；为了增加天平测量的精准度,天平刚度也设计得较弱。因此,在模型受到非定常气流激励时,支撑结构容易产生低频率大幅度振动。

图1 典型高速风洞模型支撑结构Fig.1 Typical high-speed wind tunnel model support mechanism

从大量试验模型振动问题的统计情况来看,系统的振动能量主要集中在模型纵向前2阶固有模态上。为此,对典型的飞机模型支撑结构进行模态试验,测得了纵向前2阶模态振型,如图2所示。由图可以看出,纵向第1阶模态主要表现为模型刚体平动、支杆一阶弯曲弹性振动。该模态主要由支杆的弹性引起,通常称为纵向支杆模态。纵向第2阶模态主要表现为模型刚体俯仰,天平弯曲变形,而支杆变形幅度相对较小。该模态主要由天平的弹性引起,通常称为纵向天平模态。

图2 某飞机模型支撑结构模态振型Fig.2 Modal shapes of aircraft model support mechanism

从图2还可以看出,在风洞模型支撑结构振动中,振动位移较大的是风洞模型。从振动理论可知,沿着模型振动位移方向施加控制力,可以取得最好的控制效果。但是在高速风洞试验中,为了减小支撑结构对风洞模型的气流干扰,一般不允许在模型上或模型附近增加暴露在流场中的结构。国内外实用的模型主动减振系统均是将作动器内嵌入支杆中,成为支撑结构的一部分,在控制模型振动的同时,也参与传递模型上的气动载荷。

图3给出了内嵌有压电作动器的主动减振结构工作原理示意图。压电作动器分布在支杆上、下两侧,作动方向与支杆轴线平行,通过压电作动器的差动作动,可以产生推动模型上、下运动的控制力矩。当引入测控系统形成闭环回路时,就可以通过实时控制压电作动器的输入电压,实现对风洞模型支撑结构主要模态的振动抑制。

图3 主动减振系统工作原理Fig.3 Active vibration damping system operation mechanism

由于压电作动器内嵌在支撑结构中,压电作动器作动时,需要首先克服结构的弹性恢复力,剩余的作动力才能用于推动风洞模型产生运动,因此,如果压电作动器两端的结构刚度过大,就会造成作动器作动效率低的问题。中国空气动力研究与发展中心的余立等给出了双弹性铰减振结构方案,如图4所示。该方案将直接头下部掏空,嵌入压电作动器,并在其前方设计2个弹性铰链,用于削弱结构对压电作动器的约束刚度,使主动减振结构具备减振能力。该方案中,2个弹性铰链的设计是影响减振系统减振能力的关键。

为方便叙述,本文将风洞模型支撑结构上安装压电作动器,发挥作动器能力的装配体结构,称为“主动减振结构”,或简称“减振结构”,如图4所示；将“主动减振结构”和测控系统软/硬件组成的完整系统,称为“主动减振系统”,或简称“减振系统”；将飞行器风洞试验模型简称为“风洞模型”。

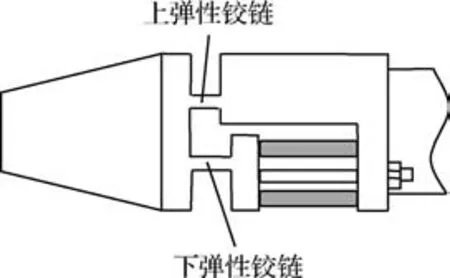
图4 双弹性铰主动减振结构Fig.4 Active vibration damping structure with double flexible joints

2 带主动减振结构的风洞模型支撑系统动力学建模

2.1 压电作动器模型

压电作动器是由经过极化的压电陶瓷薄片叠放、烧结、封装而成。陶瓷片间镀有电极,在外界电场作用下陶瓷片因逆压电效应产生法向形变。每个压电作动器的陶瓷片数量可达到数千片,因而可以在作动器轴向产生可观的位移。

按照第一类压电方程,当在陶瓷片上施加电场时,在陶瓷片法向(即压电陶瓷片的3-3方向)产生诱导应力,此时的本构方程可表达为

式中：、分别为压电陶瓷片在法向的应力和应变；为电压为常值时,压电陶瓷材料的弹性模量；为 压 电 应 力 常 数；为 陶 瓷 片 厚 度；为陶瓷片两端施加的电压。根据式(1),可得到压电作动器输出的轴向推力与其形变位移关系

式中：Δ为压电作动器伸长量；为作动器初始长度；为作动器横截面的面积；为作动器输出的轴向推力。除压电作动器的几何参数外,压电厂家一般还会提供压电作动器的最大推力和行程Δ。实际上,为压电作动器施加最大电压、伸长量Δ为0时输出的推力；Δ为作动器施加最大电压、推力保持为0时的伸长量。根据最大推力和行程Δ的物理意义,可以获得式(2)中Δ和的系数,分别为

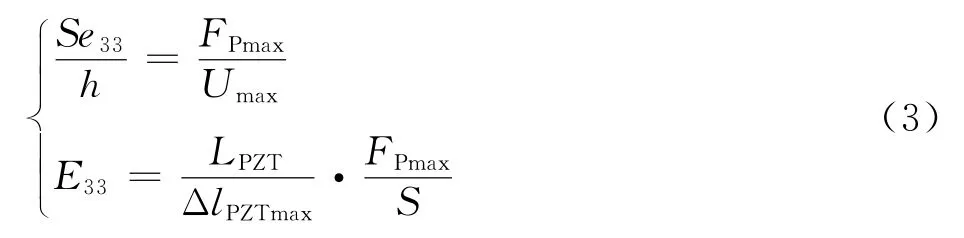
实际上,从式(2)可以看出,对压电作动器施加电压的作用效果与两端施加一对轴向拉力作用效果相同,因此压电作动器在主动减振结构中的控制力可用该等效拉力来表征,其大小为

此外,由于压电作动器通常只能承受压缩载荷,不能承受拉伸载荷,因此需要对压电作动器施加预紧力,才能实现其力和位移的连续输出。

2.2 作动器/支撑结构耦合动力学建模

配备主动减振系统的风洞模型支撑结构在非定常气流激励载荷及压电作动器作动下的耦合动力学方程可表达为

式中：、、分别为质量矩阵、阻尼矩阵和刚度矩阵,维度均为×维(为动力学系统自由度数量)；∈×1为个压电作动器的输入电压向量；D ∈×为压电作动器输入电压与等效控制力矩的转换系数矩阵,与压电作动器性能及减振结构参数有关；∈×1、∈×分别为个非定常气动力向量和激励系数矩阵。

根据式(5),求解特征方程,获得模态振型,进而得到正交化的模型振型矩阵,再令

式中：为时间；()为×1维的模态广义坐标向量。将式(6)代入式(5),经变换后可得

式中：ζ、ω分别为第阶模态阻尼比和圆频率。进一步定义状态向量

可以将式(7)改写成标准控制系统方程形式

其中,状态矩阵、控制矩阵B 及干扰传递矩阵分别为

减振结构的设计变量会直接影响系统的控制输入矩阵B ,从而影响其对风洞模型支撑结构振动的控制能力。

3 减振结构优化问题数学表达

3.1 振动模态可控性定量表征

减振结构设计的主要目标是尽可能地提高压电作动器对主要受控模态的控制能力。在优化设计中,首先要解决减振控制能力的定量表征问题。采用系统可控性的概念来描述压电作动器对风洞模型支撑结构振动的控制能力,并由此建立减振结构优化数学模型。

根据Hamdan和Nayfeh的系统可控性理论,个压电作动器对第阶模态的可控性度量表达为

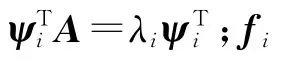
若仅需控制某一阶模态时,可直接使用式(12)作为优化目标进行优化设计,但如果需要同时控制多阶模态时,就需要考虑如何选取优化目标函数的问题。

本文引入模态价值理论,用各阶模态的价值比因子作为其可控性指标的权重系数来构建优化目标函数,基本思想是根据非定常气动载荷引起的模型系统响应能量在某个模态上的分配来表征该模态的重要程度。实际操作时,可通过天平测定动态载荷或布置加速度传感器等方法,在特定工况下估计各个模态上的振动能量,进而将第阶模态的价值比因子表达为

式中：E为第阶模态上的振动能量；为各阶模态振动能量总和。

3.2 优化目标函数

根据3.1节的模态可控性定量表征和模态价值分析方法,可以给出用于定量描述主动减振结构设计优劣的评价函数,计算公式为

式(14)的优化目标是各阶模态可控性函数张成的维空间椭球体体积,当其达到最大值时,可以确保整个系统各阶模态的可控性都达到一个较理想的值。

3.3 约束性指标

3.3.1 结构强度和刚度

主动减振结构设计时,需要保证结构在极限载荷情况下有足够的安全裕度。通常,最需要关注结构强度的部位主要是弹性铰链、压电作动器及预紧螺栓等。这些部位的强度裕度往往与系统可控性指标矛盾,需要在减振结构优化设计中加以考虑。

如果主动减振结构的第个零件(或部位)在最恶劣载荷工况下的应力为σ,该零件材料的许用应力为[σ],则该零件的强度安全系数f可表达为

式中：=1,2,…,N ；N 为需考虑强度问题的零件或部位数量。在优化设计中,可以使用强度安全系数作为约束条件,表达式为

式中：为许用的最低安全系数。

此外,减振结构设计时,弹性铰链等结构的刚度不能设计得过小,否则会显著削弱主动减振结构的刚度,进而造成风洞模型支撑结构振动情况的进一步恶化。在设计时,可以通过限制减振结构与原准结构的刚度比值来满足这一指标要求,即

式中：、分别为原准结构和减振结构的整体刚度；为允许的刚度比值下界。

3.3.2 压电作动器非均匀载荷

由于压电作动器不能承受大的剪切载荷和弯曲载荷,减振结构设计时,需要尽量减小作动器安装结构的扭曲,让压电作动器受力顺畅、均匀。

对于弹性铰形式的减振结构,主要需要限制压电作动器所受到的弯曲载荷。压电作动器所受的最大弯曲载荷需满足

式中：为压电作动器允许的最大弯曲载荷。

3.4 优化问题数学表达

根据上述优化目标函数构建方法及约束性指标,可以获得给出风洞模型主动减振结构的优化问题数学表达

式中：x 为第个设计变量,其几何边界分别为 、 (即每个设计变量允许的取值范围,具体与风洞支撑外形的设计要求有关)；N 为设计变量的数量。

4 算例分析

4.1 简化动力学模型

针对某典型飞机风洞试验模型的主动减振结构,应用本文提出的方法进行优化设计,以检验本文方法的有效性。

如图4所示,该主动减振结构需控制的振动模态为风洞模型支撑结构的纵向支杆模态和天平模态,而设计的关键部位为2个弹性铰链和预紧螺栓。为了更加清晰地展示优化过程,依据主动减振系统的控制原理对支撑结构进行了简化处理,并建立了解析的动力学/控制耦合模型。

如图5所示,简化模型仅考虑风洞模型支撑结构纵向支杆模态和天平模态,主要对风洞试验模型、天平和支杆进行简化处理,而对于主动减振结构,则基本保持与实际结构一致。依据图2所示的模态振型,将天平和支杆的结构弹性简化为2个扭转弹簧和；风洞模型、支杆均假设为有质量刚体；风洞模型质心与支杆前端距离为；支杆长度为；风洞模型上作用有法向载荷 和俯仰力矩M ,且作用点在风洞模型重心轴负方向,与重心距离为；上、下2 个弹性铰链、压电作动器及预紧螺栓等由于对振动模态质量贡献小,均假设为有弹性、无质量,可伸缩变形和弯曲变形的梁；与2个铰链及压电作动器连接的结构均假设为无质量的刚性结构；所有压电作动器输入电压保持同步,均为()。各参数如表1所示。

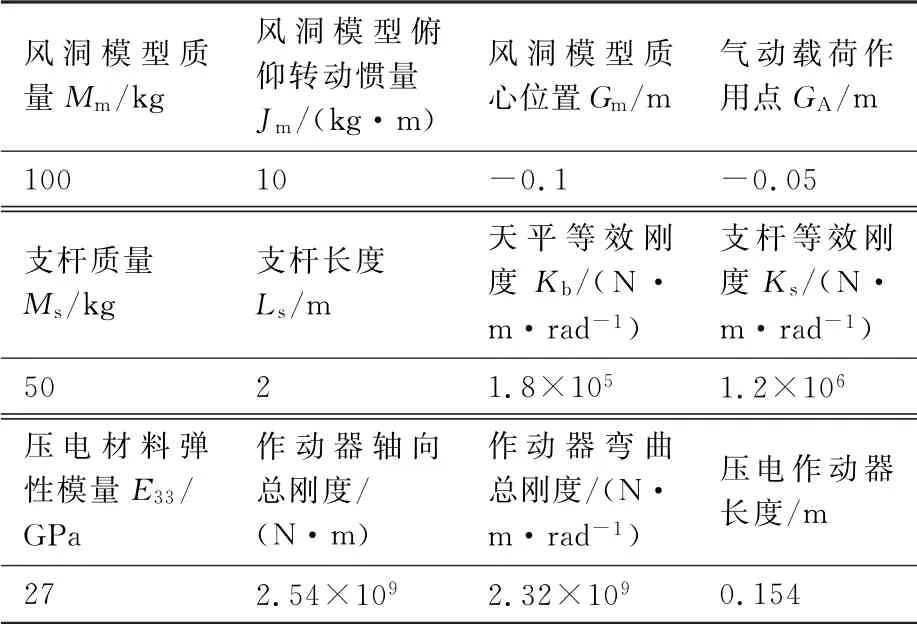
表1 简化模型参数Table 1 Parameters of idealized system

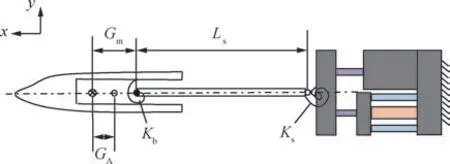
图5 简化的支撑系统动力学模型Fig.5 Idealized model for sting-support model system

应用拉格朗日方程建立该简化模型的动力学方程。拉格朗日方程形式为

该简化动力学模型需要考虑的动能为风洞模型的竖直方向平动动能、俯仰转动动能及支杆旋转动能；需要考虑的势能为预紧螺栓、压电作动器、上铰链及下铰链的拉压势能,预紧螺栓、压电作动器、上铰链、下铰链的弯曲势能,以及支杆、天平等效扭转弹簧的势能。

采用虚功原理,可以获得系统的广义力。选取广义变量=[,,Δ],其中,、分别为支杆和风洞模型的俯仰角。系统的虚功为

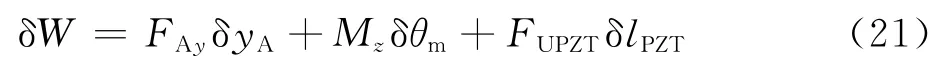
式中：δ为风洞模型气动力作用点位移变分,δ=δ+δ；为式(4)给出的压电作动器等效输出力；δ、δ、δ分别为各广义变量的变分。

运用拉格朗日方程可得到如下形式的动力学方程组

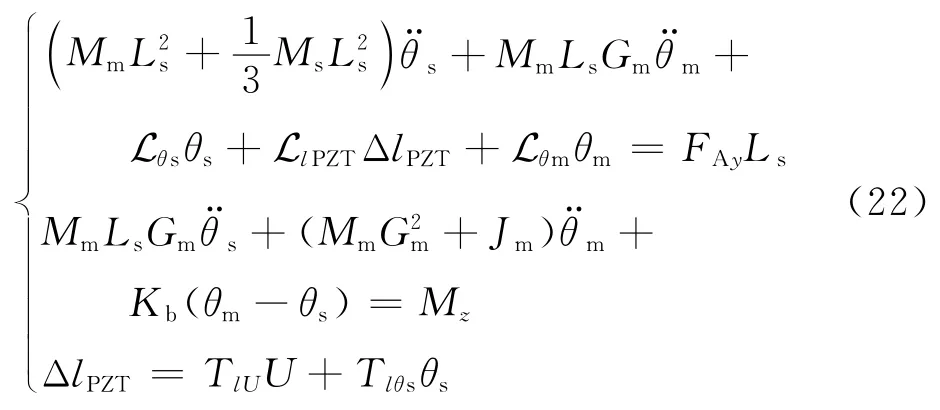
式中：L、L 、L分别变量、Δ、所对应的系数,均为表1中系统参数的函数；T 、T 分别为压电作动器输入电压、所对应的系数。从式(22)可以看出,系统独立的自由度仅有2个,因此可以整理为形如式(5)的标准动力学方程,其中

在此基础上,使用2.2节中的方法可以获得标准控制系统方程式(10)以及状态矩阵、控制矩阵B 。

此外,为了检验简化模型与实际模型支撑结构的一致性,使用表1中的参数计算简化动力学模型的模态特性。简化模型的模态频率及其对应的正交化模态振型如表2所示。由于表征支杆变形大小,-表征天平变形大小,对比两阶模态振型,可以看出：一阶模态主要表现为支杆的变形,二阶模态主要表现为天平变形、模型俯仰转动；简化模型动力学特性与原支撑结构基本一致。

表2 简化模型模态特性Table 2 Modal characteristics of idealized system

4.2 主动减振结构参数优化

本算例中,减振结构优化的主要目的是对图6所示的上下2个弹性铰链的几何尺寸、位置,以及预紧螺栓的直径进行优化,在满足强度、刚度、压电作动器非均匀载荷等约束条件下对减振结构振动控制能力进行提升。图6给出了铰链的几何参数定义(上、下弹性铰链的宽度、沿图的法向,图中未给出)。表3给出了铰链及预紧螺栓的初始设计值,并根据实际结构几何约束给出了各个设计变量的变化范围。

表3 设计变量初始值及边界Table 3 Original and boundary values of design variables

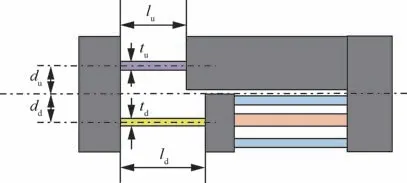
图6 弹性铰链的设计变量Fig.6 Design variables of flexible joints

根据第3.4 节中的优化目标函数及约束条件,令：2个弹性铰链及预紧螺栓的强度安全系数许用值=2.5；每个压电作动器允许的最大弯曲载荷=5 N·m；引入铰链后,风洞模型支撑结构刚度不低于原准结构的90%,即=0.9。此外,在计算预紧螺栓的应力时还考虑了每根螺栓上存在预紧力80 k N。

根据风洞试验中天平测得的动态载荷及支撑结构的刚度,对非定常气流激励产生的振动在纵向支杆模态和天平模态上分布的能量比例进行了估算。多次试验统计结果显示,对于典型的试验状态,支杆模态与天平模态能量比例约为1∶8。因此,式(13)的模态价值比因子可分别取为

根据式(19),该简化模型的优化问题数学模型可表示为

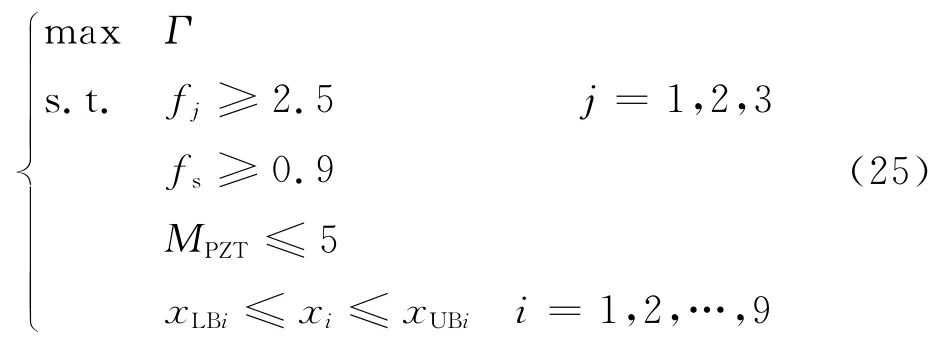
为了使用遗传算法求解以上优化问题,需要将式(25)改为标准的最优化形式,并将约束条件用罚函数法引入优化目标中,可得到适用于遗传算法进行求解的表达形式

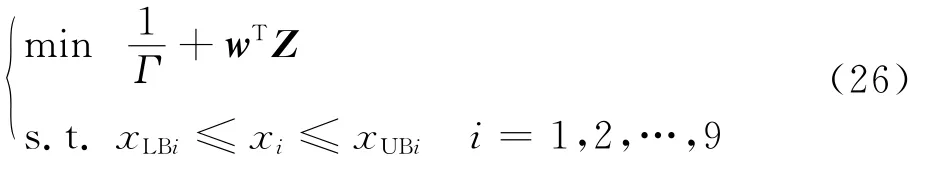
式中：为约束条件的惩罚因子向量；为各约束条件,可取为

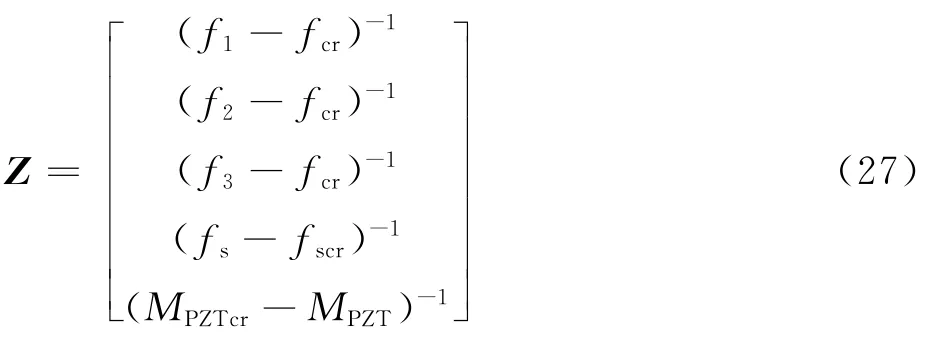
采用如图7所示的优化计算流程,对上述的优化问题进行求解。优化前后,减振结构各项指标对比如表4所示。由表4可以看出,使用本文方法对主动减振结构进行优化后,对风洞模型支撑结构纵向支杆模态的可控性提高了75%,对纵向天平模态的可控性提高了63%。同时还可以看出,减振结构的强度、刚度等指标都较初始设计有较大幅度降低,表明主动减振结构的控制能力指标与约束性指标此消彼长,相互制约。

表4 优化前后各项指标对比Table 4 Comparison of indexes before and after optimization

图7 优化计算流程图Fig.7 Flowchart of optimization procedure

为验证优化结果,将优化前、后的设计变量分别代入动力学方程式(22)进行时域仿真。压电作动器以相同的输入电压幅值(取100 V)分别在2阶模态固有频率上激励,通过对比优化前、后风洞模型支撑结构的时域响应幅值,来检验优化对振动模态控制能力的提升。在仿真中,优化前、后系统的各阶模态阻尼比均取为0.01。图8(a)给出了以支杆模态固有频率激励时,试验模型重心在铅锤面内的振动位移响应；图8(b)给出了以天平模态固有频率激励时,试验模型俯仰角响应。可以看出,优化后主动减振结构对2阶模态的控制能力都有较大幅度提高,证明了本文优化方法的有效性。

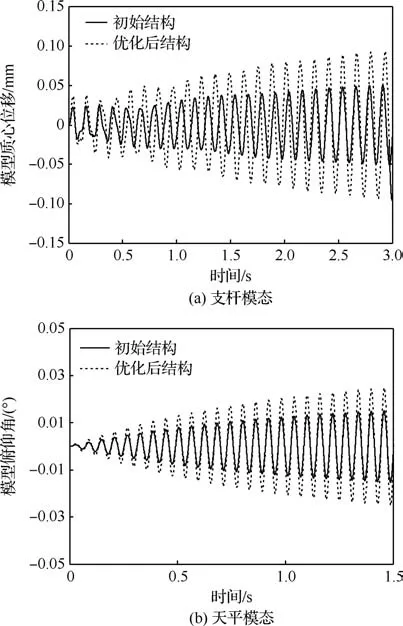
图8 优化前后系统激励能力对比Fig.8 Comparison of excitation capacity between original and optimized structures

4.3 设计变量敏感性分析

使用优化方法获得的优化结果往往只是数学上的最优解,实际设计中还需要考虑加工工艺和成本等因素。对一些需要投入很大加工成本才能实现的设计,需要考察其是否有必要予以严格保证。因此,对设计变量进行敏感性分析,确定出关键变量及其重要性排序,在实际工程中具有重要意义。

在优化结果基础上,让每个设计变量在一定范围内依次单变量变化,计算模态可控性及约束指标的变化。本文选取第个设计变量的变化范围为[x -10%×( - ),x +10%×( x )]。此外,为了清晰地反映每个设计变量影响量的相对大小,引入归一化函数进行处理,即将第个设计变量对第个指标的相对影响量~I 表达为

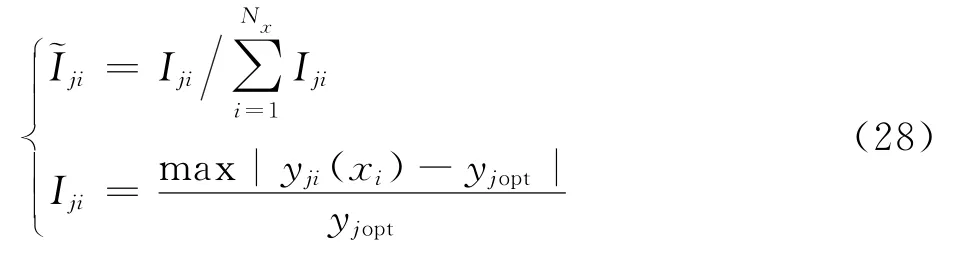
式中：y (x )为第个设计变量变化时第个指标对应的值；y 为最优化设计下第个指标的值。

设计变量对各个指标的敏感性分析结果汇总如表5所示。从表5可以看出,在优化结果附近,影响支杆模态和天平模态可控性指标、的主要设计变量相同,均为上/下铰链厚度、上/下偏置距离及预紧螺栓直径。同时,这5个设计变量也是对整个风洞模型支撑结构刚度系数影响相对最显著的设计变量。这一分析结果与前述主动减振结构的工作原理相吻合,即压电作动器需首先克服主动减振结构的弹性恢复力,剩余作动力用于推动模型产生运动。因此,设计时需要合理平衡减振结构能力与刚度的指标要求。

观察表5中上、下铰链强度安全系数、,可以发现,2个铰链的设计存在严重耦合。改变一侧铰链的几何参数,另一侧铰链的强度安全系数也会发生大幅度改变。预紧螺栓强度安全系数仅受螺栓直径影响,而对其他设计变量均不敏感。

表5 设计变量敏感性分析结果Table 5 Sensitivity analysis of design variables

对于压电作动器所受到的弯曲载荷,其主要影响参数为下铰链的偏置。进一步分析发现,压电作动器、预紧螺栓及两侧的质量块形成一个舱体结构,当下铰链偏离该舱体结构的刚心时,压电作动器所受弯曲载荷会急剧增大。因此,在确定下铰链的偏置位置时,应优先考虑将下铰链布置在该舱体结构的刚心附近。

此外,从表5还可以看出,上、下铰链的长度、宽度4个变量对可控性指标及各约束指标的影响较小,对于本算例来说均是非关键设计变量。因此,可根据实际需要对其进行适当调整,而不会对系统的各个指标造成显著影响。

5 结 论

1)结合模态可控性理论和模态价值理论的减振能力定量描述方法,能够综合考虑实际工况下各模态的振动能量分配,是评判主动减振结构能力优劣的有效手段。

2)风洞模型主动减振结构设计问题是典型的非线性问题。本文方法先进行优化计算,再以优化结果为基准状态进行敏感性分析,可以较为准确地给出主动减振结构各设计变量对设计指标的影响程度,从而找出关键设计变量。

3)采用本文方法对主动减振结构进行优化设计,能在满足约束指标要求前提下,有效地提高压电作动器对风洞模型支撑结构主要模态的可控性,进而提高主动减振系统的抑振效果。