动态优先级解耦的无人机集群轨迹分布式序列凸规划
2022-03-29徐广通王祝曹严孙景亮龙腾
徐广通,王祝,曹严,孙景亮,*,龙腾
1.北京理工大学 宇航学院,北京 100081
2.飞行器动力学与控制教育部重点实验室,北京 100081
3.华北电力大学 河北省发电过程仿真与优化控制技术创新中心,保定 071003
近年来,无人机集群智能技术在军事与民用领域得到了愈来愈广泛的研究。无人机集群快速轨迹规划是实现集群智能化的一项瓶颈技术。集群轨迹规划是指在有限空间维度下为大量无人机规划出连续平滑的协同轨迹,满足机间避碰、威胁规避及无人机动力学等约束,实现无人机之间高效的任务协作。然而,严格的威胁规避约束、耦合的机间避碰约束以及非线性无人机动力学导致了集群轨迹规划难以快速求解,无法满足集群在线轨迹规划要求。因此,如何通过处理机间耦合关系来提升求解效率是快速轨迹规划的关键。
优先级规划作为解耦规划的主要分支,可使无人机按照优先级次序依次进行规划。该方法因其降低了集群轨迹规划的耦合度,提升了集群轨迹规划效率,得到了国内外学者的广泛研究。Van Den Berg和Dvermars提出一种基于运动距离的启发式优先级确定规则,能够在15 s内完成包含24个智能体的几何航路规划,但未考虑智能体非线性动力学约束。Robinson 等使用串行优先级解耦机制与伪谱法求解异构旋翼机协同轨迹规划问题,32 架机轨迹规划耗时累计为112 s。然而,该方法使用预设式优先级生成方法,导致解耦规划易于陷入不可行状态。Prasanna等提出了同步并行优先级解耦机制,并在理想通信条件下完成了算法的收敛性证明,仿真结果表明240个智能体的并行迭代一般可在20次以内收敛,相比串行方式可以大幅减少规划耗时。2015年,Cap等提出了改进的并行优先级规划方法,进一步节省了同步规划方法中个体相互等待时间,更加充分地利用集群计算资源,相比于同步规划方法,25个智能体轨迹规划效率提升了1倍。但是,上述并行优先级规划方法均未考虑多智能体的时间协同约束,难以实现编队形成与变换等任务。
除了高效的解耦机制外,数值优化方法也是制约集群轨迹规划效率的关键之一。近年序列凸规划(SCP)开始应用于多智能体协同轨迹规划问题。苏黎世联邦理工学院D’Andrea团队于2012年首次利用SCP 方法以耦合规划方式实现了12架无人机的避撞轨迹规划,每个迭代求解子问题是关于集群轨迹的二次规划问题。文献[11]结合罚函数与耦合的SCP方法,能够在40 s内为7架固定翼无人机规划出编队集结轨迹。为缓解耦合规划时效性不足问题,麻省理工学院Chen等使用串行优先级解耦规划机制与SCP 方法,依据优先级次序利用SCP逐个求解每架无人机轨迹,能够将10架四旋翼编队轨迹规划耗时由40 s降到4 s。Chung等针对固定时间航天器集群轨迹规划问题,提出并行解耦SCP 方法,降低了计算复杂度,将航天器集群无障碍环境下轨迹规划时间缩短到几十秒。在此基础上,Wang等使用并行解耦SCP 求解多无人机时间最优轨迹规划问题,能够在13.5 s内生成7架机编队集结轨迹,满足动力学、障碍规避与机间避碰约束。然而,文献[14]所提并行解耦SCP处理机间避碰约束可能陷入迭代振荡,难以获得可行解。另外,该研究未给出并行SCP求解集群轨迹规划问题的时间一致理论分析。Lu针对非线性等式约束提出凹凸分解的SCP方法,将一个等式约束转化为3个不等式约束,但是该方法难以处理非线性动力学约束。Foust等提出一种飞行器非线性动力学修正的SCP方法,以牺牲计算效率为代价提升了SCP的求解精度,且仅涉及小规模无人机的协同轨迹规划。
针对高维强耦合的集群轨迹规划问题,本文结合优先级解耦机制与SCP方法,发展动态优先级解耦的集群轨迹分布式规划方法,实现集群轨迹并行规划,改善轨迹迭代收敛速度。本文主要贡献为:①提出了动态优先级解耦的序列凸规划方法(DPD-SCP),将连续时间集群轨迹规划问题转化为一组单机凸规划子问题,降低问题求解复杂度。②发展了飞行时间驱动的动态优先级解耦机制,解决迭代振荡问题,改善集群轨迹解耦规划的收敛性;定制时间一致约束更新准则,调整飞行时间下边界约束,驱使集群同时抵达终端位置,形成既定编队构型。③理论证明了所提方法能够获得满足协同约束的集群轨迹;数值仿真结果表明,DPD-SCP相比耦合SCP、串行优先级解耦SCP以及并行解耦SCP具有明显的效率优势。
1 无人机集群轨迹解耦规划问题建模
集群轨迹解耦规划是指每架无人机根据自身任务、他机轨迹、威胁等信息,并行规划出最小飞行时间协同轨迹。图1 为集群轨迹解耦规划示意,每架无人机基于共享的轨迹信息规划本机轨迹,通过不断的轨迹迭代确保集群时空一致性。
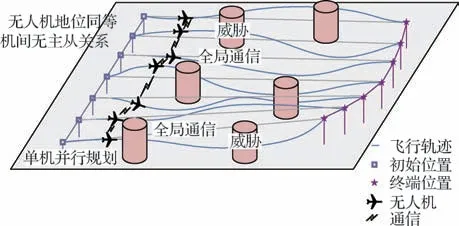
图1 无人机集群轨迹规划示意图Fig.1 Illustration of trajectory planning for UAV swarms
1.1 无人机动力学建模
考虑存在架具有相同飞行性能的固定翼无人机,基于欧拉角建立三自由度无侧滑动力学模型,如式(1)所示:

式中:

无人机动力学状态变量s ∈R包括无人机三维空间位置p =[p ,p ,p ]、飞行速度V 、航向角χ以及航迹倾角γ,即s =[p ,p ,,p ,V ,χ,γ]。控制变量u ∈R包括切向过载n 、法向过载n 与垂直过载n ,即u =[n ,n ,n ]。表示重力加速度,下标为无人机索引,代表第架无人机。
1.2 解耦的非凸轨迹规划问题建模
利用配点法离散化状态与控制变量,将轨迹时间[,]拆分成等步长的个区间,离散步长为Δ=(-)/。使用离散处的+1个点近似表示轨迹,其中t =+·Δ,=0,1,…,。解耦的轨迹规划问题设计变量X 包含单机状态与控制变量及时间步长Δt,即X =[ ,Δt],其中z =[s [],u []],=0,1,…,。无人机考虑的初始与终端状态[s ,s ]、状态与控制边界[,,,]、动力学以及威胁规避约束,均不涉及他机轨迹信息,分别如式(3)~式(6)所示。
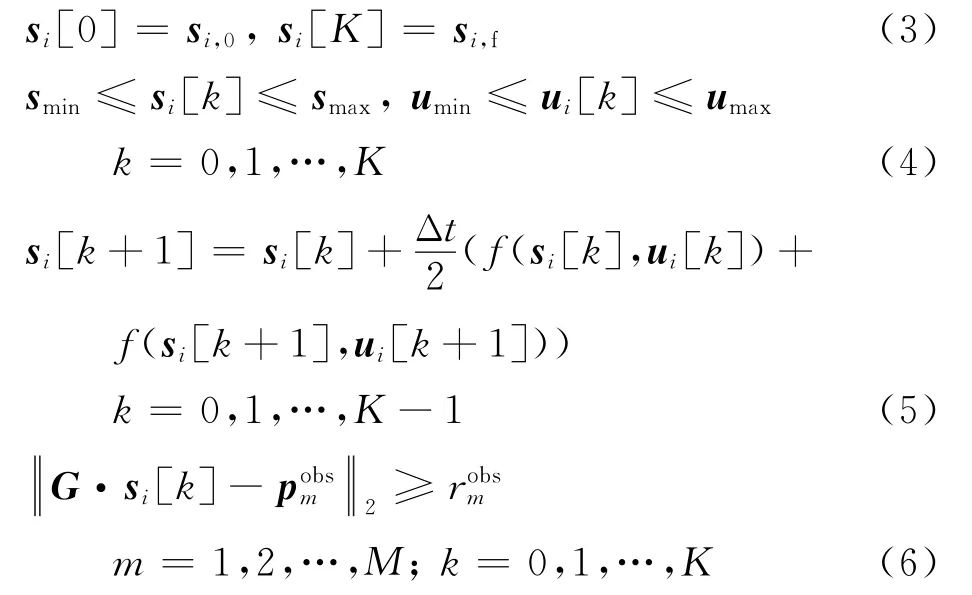
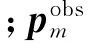
针对无人机碰撞规避问题,建立如式(7)所示的机间避碰约束,其中表示机间安全距离限制,确保无人机安全性。
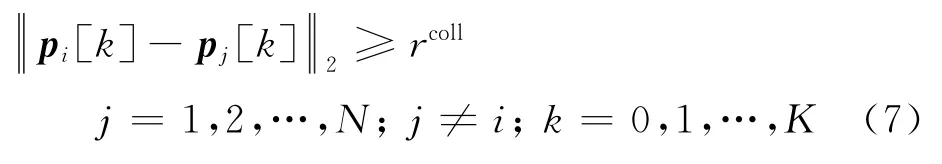
为实现无人机集群同时抵达终端位置,无人机之间需要分享彼此飞行时间信息,并设定离散时间步长下边界约束,如式(8)所示。通过延长飞行时间短无人机的时间步长,或调整无人机的飞行速度,使得所有无人机飞行时间趋于一致,保证无人机集群形成预设的编队队形。
式中:Δ表示集群轨迹规划的时间步长下边界值,具体取值方法详见2.4节。
考虑机间避碰与时间协同约束,建立无人机-的非凸轨迹规划问题模型P1,如式(9)所示:
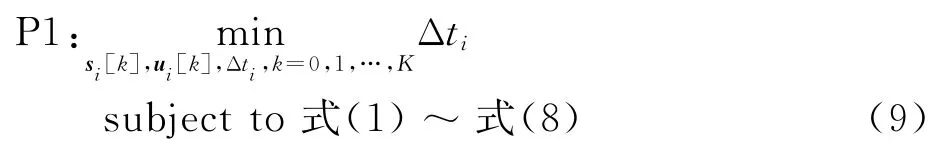
2 动态优先级解耦的序列凸规划方法
本节首先建立集群轨迹凸规划子问题,然后设计分布式轨迹规划架构,详细描述动态优先级解耦机制与时间一致约束更新准则,最后给出动态优先级解耦的序列凸规划算法具体流程。
2.1 解耦的凸规划子问题建模
使用一阶泰勒展开将非线性动力学与非凸威胁规避约束凸化为式(10)与式(11)的仿射约束。
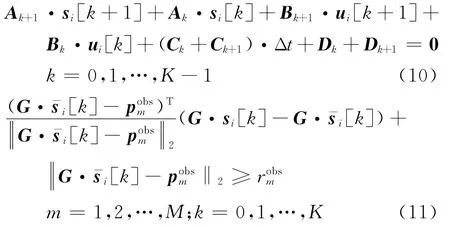
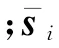
另外,针对耦合的非凸机间避碰约束,基于轨迹冻结思想,在单机轨迹规划每一步迭代中将其他无人机轨迹视为固定不变,每架无人机仅需规避他机的冻结轨迹点位置,即上一步迭代结果。由于冻结轨迹在每次规划时已知,因此避碰约束仅包含无人机-的状态变量,实现避碰约束解耦。在此基础上,使用一阶泰勒展开凸化解耦机间避碰约束,得到式(12)所示的仿射形式。

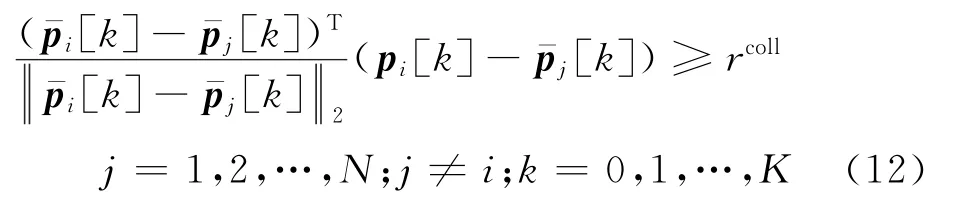
引入信赖域约束,通过非凸约束凸化,建立集群轨迹的解耦凸规划子问题,如式(13)所示,其中=[ρ,ρ,ρ,ρ,ρ,ρ]为信赖域半径。
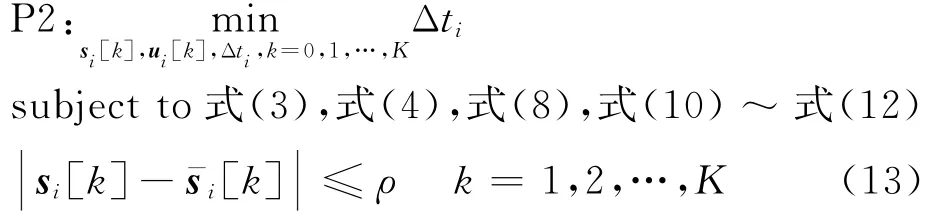

2.2 分布式轨迹规划架构
分布式体系架构中无人机处于同等地位,相互之间不存在主从关系。分布式架构依赖无人机之间的通信,通过迭代求解实现机间协同。因此,本节给出理想通信假设(假设1):集群个体间保持两两通信,能够有效获取彼此的轨迹信息,不考虑通信数量、通信距离、通信带宽、通信延迟等约束。
无人机集群分布式轨迹规划本质上是一个计算平台并行迭代求解方法,架构如图2所示。在每一轮迭代中,各无人机考虑本机动力学、威胁规避与解耦的机间避碰等约束,构建各自的单机轨迹规划凸规划子问题P2。针对耦合的机间避碰约束,每架无人机仅考虑规避其他无人机上一步迭代的轨迹,不考虑当前迭代步他机轨迹的更新,通过轨迹暂时冻结实现机间避碰与时间一致约束解耦。每次迭代中,无人机独立求解本机轨迹规划问题,无人机之间没有信息交互,计算较快无人机需等待他机完成本轮轨迹解算。在每一轮迭代结束后,无人机之间通过通信传输彼此最新的轨迹信息,为下一轮迭代提供冻结轨迹信息。无人机根据获取的他机轨迹信息,更新时间步长下边界约束,建立解耦的机间避碰约束,进行新一轮计算,直到获得满足飞行约束的轨迹。
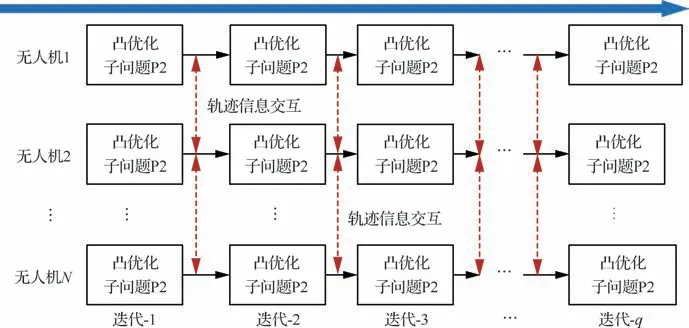
图2 无人机集群轨迹分布式规划框架Fig.2 Framework of distributed trajectory planning for UAV swarms
无人机集群协同飞行的密集特征与动态特性给算法快速求解可行轨迹带来了更加严苛的条件。由于无人机规避他机冻结轨迹,在密集高动态集群环境下,基于相互避碰机制的轨迹迭代可能出现振荡而难以收敛的问题。为此,本文设计了飞行时间驱动的动态优先级解耦机制(具体见2.3节),改善轨迹迭代的收敛性。基于轨迹冻结思想,无人机规避的他机冻结轨迹与实际轨迹的偏差在信赖域的约束范围内,且随着迭代进行信赖域半径逐渐缩小,冻结轨迹与实际轨迹的偏差降低。当序列迭代收敛时,冻结轨迹与实际轨迹趋于一致。因此,基于轨迹冻结思想的分布式规划能够获得满足约束的集群轨迹。
2.3 飞行时间驱动的动态优先级解耦机制
在基于轨迹冻结思想的解耦规划框架下,不合理的机间避碰约束处理机制可能导致集群轨迹规划难以收敛。在轨迹迭代过程中,各无人机通信仅得到他机上一步迭代的轨迹信息,而未获取他机当前的轨迹信息。在无人机相互规避机制下,轨迹迭代可能出现振荡情况。图3为机间避碰反复振荡示例,在第次迭代时,由于无人机-考虑规避无人机-第-1次迭代的位置,无人机-在虚线所示的安全区域外飞行,逐渐靠近无人机-当前位置。在下一轮+1次迭代时,相互避碰机制将会保守的驱使两架无人远离彼此。后续迭代中两架无人机可能反复靠近与远离,难以获取满足避碰约束的轨迹。
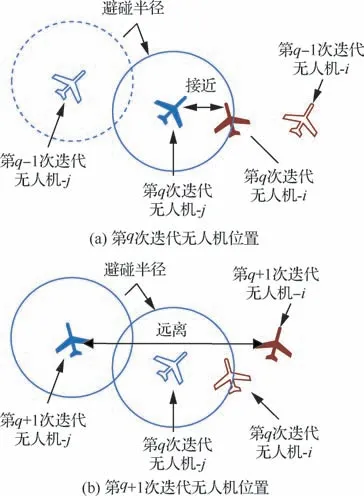
图3 碰撞规避振荡现象示意图Fig.3 Illustration of collision-avoidance oscillation
为了处理上述问题,使用优先级驱动的单向避碰规则,给无人机分配高低优先级,低优先级无人机进行轨迹规划时,需规避高优先级无人机,而高优先级无人机无需考虑对低优先级个体的规避,从而避免无人机相互避碰而引起的轨迹迭代振荡问题。图4给出了6架无人机优先级次序示例,其中P 表示无人机优先级,下标=1,2,…,为无人机编号,上标=1,2,…,为优先级等级。例如,P表示无人机-1优先级等级为3,需要规避无人机-2、无人机-5与无人机-6;P表示无人机-3优先级最低;P表示无人机-5具有最高的优先级,无需考虑机间避碰约束。

图4 避碰优先级示意图Fig.4 Illustration of collision-avoidance priority
不同的优先级生成方法对于集群轨迹规划收敛速度具有重要影响,合适的优先级可以提高集群解耦轨迹规划效率。本文提出飞行时间驱动的动态优先级生成方法,在每次迭代结束后,根据无人机冻结轨迹对应飞行时间,自适应调整无人机优先级次序,改善轨迹规划的收敛性。无人机-的优先级评价指标κ取为无人机-从起始点到目标点的飞行时间·Δt,如式(14)所示:

由于飞行时间短无人机具有更多的剩余飞行空间,其成功规避他机的概率更高,因此对飞行时间短的无人机分配低的优先级,充分利用该类无人机的剩余飞行空间进行轨迹调整。若2架无人机飞行时间相同,则随机分配其优先级次序。
根据飞行时间·Δt确定集群优先级关系,将无人机-所需规避的无人机集合Π表示为
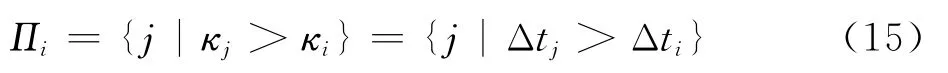
根据优先级确定的无人机规避集合,集群内无人机的避碰约束可表示为
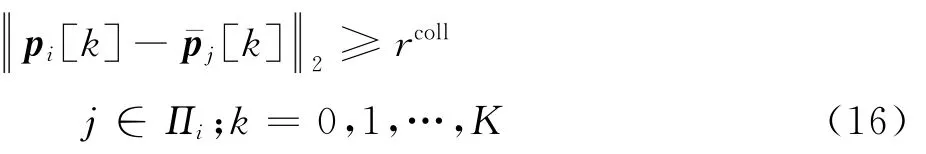
在每一轮迭代求解结束后,动态优先级生成机制根据新生成的轨迹信息,对无人机优先级次序进行调整,如式(17)所示:

针对任意2架无人机,如果原高优先级无人机飞行时间小于低优先级无人机,且时间差大于阈值,则进行优先级次序互换,否则优先级次序不变。若低优先级无人机飞行时间仍然小于高优先级无人机,则优先级次序保持不变。基于所设计的动态优先级生成方法,只有无人机飞行时间变化超过一定范围后才进行优先级调整,避免微小变动引发的优先级次序反复变化问题。
2.4 时间一致约束更新准则
针对集群解耦轨迹规划时间一致问题,增加了时间步长下边界约束Δ。考虑到凸规划子问题中的动力学约束是线性近似的结果,无人机轨迹迭代过程中存在前后两次迭代结果相差较大的情况,因此直接取所有无人机轨迹离散步长最大值作为时间步长下边界,可能导致整体飞行时间的显著增大。为了避免该现象引起集群飞行时间下限非正常增长的情况,在计算时间步长下限时,仅考虑连续两次迭代中时间步长变化较小无人机的飞行时间,如式(18)所示:
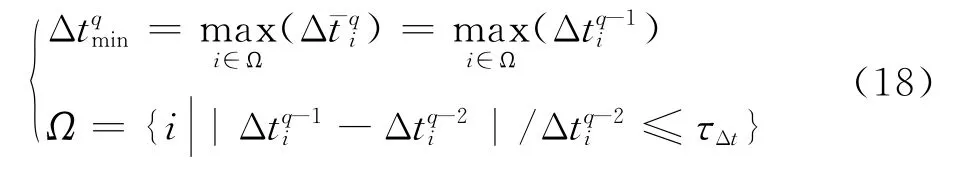
式中:表示时间步长变化判断阈值;上标表示轨迹迭代索引。
2.5 动态优先级解耦的序列凸规划算法流程
DPD-SCP方法求解流程主要包括3个阶段,初始直线轨迹生成的第1阶段,不考虑避碰约束的第2阶段和考虑所有约束的第3阶段。第2和第3阶段需要满足式(19)所示的时间一致收敛条件,其中表示集群时间一致收敛阈值。
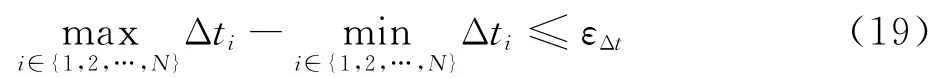
动态优先级解耦的序列凸规划伪代码如算法1所示,具体流程如下所述。

算法1 动态优先级解耦的序列凸规划算法
初始化算法。初始化算法参数,包括轨迹离散时刻数量、状态收敛阈值∈R、初始信赖域半径、时间一致收敛阈值、时间步长调整阈值、优先级动态调整阈值。输入无人机的初始与终端状态[s ,s ]、状态与控制边界约束[,]和[,]、威胁集合等信息。
(第1~3行) 生成初始轨迹与初始优先级。使用线性插值为每架无人机规划出连接起始点与目标点的直线轨迹,为后续轨迹迭代提供初值。基于式(15)所示的优先级生成方法,根据初始轨迹时间步长,确定无人机所需规避的他机集合Π。
(第4~13行) 规划满足动力学与时间一致约束的轨迹。迭代过程中,使用式(18)计算时间下边界值Δ,逐次建立并求解考虑无人机动力学、初始与终端状态、状态与控制边界、时间一致约束的凸规划子问题。根据上一步迭代的轨迹信息,使用式(17)更新无人机规避集合Π。该阶段不断迭代求解,直到生成满足收敛条件(20)的轨迹,其中表示状态收敛阈值。
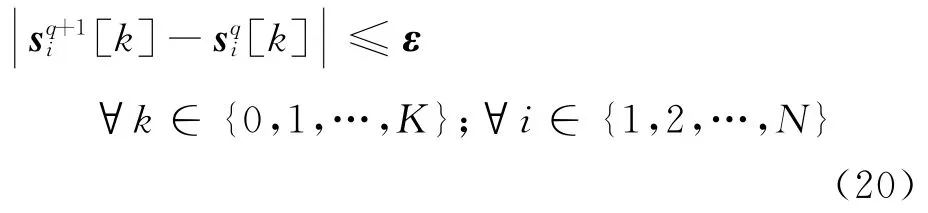
(第14~25行) 规划满足全部约束的协同轨迹。本阶段重新给信赖域赋初始值。在步骤3生成轨迹的基础上,考虑碰撞规避约束,使用所提动态优先级解耦机制,迭代规划出满足动力学、碰撞规避、时间一致等约束及收敛条件(20)的集群轨迹。
3 集群轨迹分布式序列凸规划收敛性分析
本节首先给出理论分析所依赖的基本假设,然后分析DPD-SCP求解集群轨迹规划问题的收敛性,并给出定理1及其证明。
假设2(集群非凸轨迹规划问题解存在性):无人机集群非凸轨迹规划问题(P1)至少存在一个可行解,满足初始与终端状态、状态与控制边界、动力学、威胁规避、机间避碰与时间一致约束。
在假设2解存在性的基础上,针对转化的集群轨迹规划的凸规划子问题P2,如果序列凸规划方法生成有限或无限序列{X },则{X }能够收敛到至少一个极值点,即序列凸规划至少能够求解得到问题P2的一个局部最优解。
问题P2中动力学约束为仿射等式形式,初始与终端状态约束为线性等式形式,状态与控制边界、威胁规避、机间避碰以及信赖域约束均为仿射不等式形式,因此问题P2 所考虑的约束构建了一个凸紧集。由于问题P2的目标函数在凸紧集上是连续可微的,依据Bolzano-Weierstrass定理,在凸紧集中问题P2 至少存在一个极值点,即局部最优解。
若解耦的非凸轨迹规划问题P1包含可微目标函数、如式(6)与式(7)所示的威胁规避与机间避碰凹不等式约束、如式(1)所示的无人机非线性动力学等式约束,序列凸规划能够通过迭代求解获得原非凸轨迹规划问题P1的局部最优解。
引理1说明了序列凸规划能够获得问题P2的局部最优解。下面重点分析问题P2 的局部最优解同样是问题P1局部最优解。
针对考虑凹不等式约束(机间避碰与威胁规避)的轨迹规划问题,文献[19]利用凹约束Hessian矩阵负定特性,证明了序列凸规划能够得到凹不等式约束下轨迹规划问题的局部最优解。
针对考虑无人机非线性动力学等式约束的轨迹规划问题,文献[20]基于罚函数方法,证明了序列凸规划能够得到非线性动力学约束下轨迹规划问题的局部最优解。
综上分析可得序列凸规划方法能够得到非凸轨迹规划问题P1的局部最优解。
针对非凸轨迹规划问题P1,在分布式轨迹规划架构下,通过设计飞行时间驱动的动态优先级解耦机制,定制时间协同约束更新准则,使得DPD-SCP能够收敛到满足机间避碰与时间一致约束的集群轨迹。
基于引理1与引理2,序列凸规划能够为每架无人机规划出满足初始与终端状态、状态与控制边界、无人机动力学、威胁规避约束的局部最优解。
针对机间避碰约束,DPD-SCP基于轨迹冻结思想实现问题解耦。随着轨迹序列迭代过程进行,信赖域半径逐渐缩减,由式(21)可知迭代的轨迹逐渐变得与冻结轨迹一致。
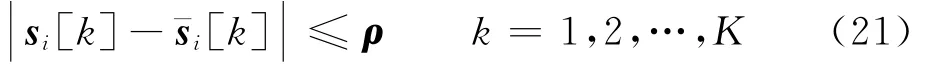
当轨迹规划收敛时,无人机规避的他机轨迹即为最新轨迹。因此,最终的集群轨迹结果能够满足机间避碰约束。
后续基于反证法重点分析DPD-SCP 能够收敛到时间一致的集群轨迹。
不失一般性,第次迭代,无人机-以最小化飞行时间为目标函数,考虑时间下边界约束(18),通过序列规划得到满足约束的飞行时间结果,如式(22)所示:

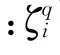

DPD-SCP求解得到每架无人机飞行时间为

考虑动力学约束与时间下边界约束包含时间步长信息,为便于推导,建立仅考虑动力学约束与时间下边界约束的凸规划子问题P3。
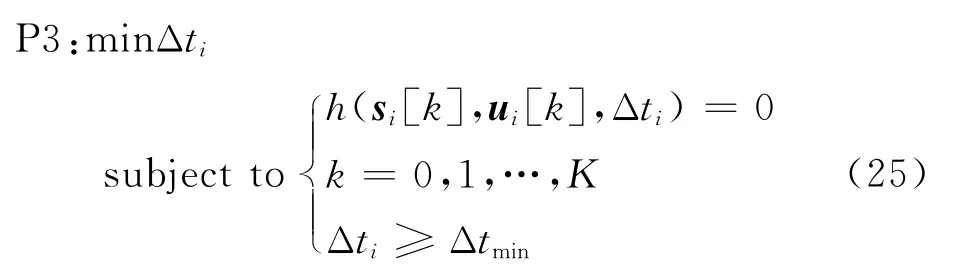
式中:(s ,u ,Δt)=0表示线性化后的动力学等式约束。推导P3 的Karush-Kuhn-Tucker(KKT)条件,如式(26)所示:

式中:h 为动力学约束求偏导后的常值;h 与冻结轨迹相关,与当前设计变量X 无关;λ与分别表示等式与不等式约束的拉格朗日乘子。
若第次迭代-Δt+Δ=0,则时间下边界约束成为主动约束。若Δt>Δ,根据KKT条件第1项与第4项,迭代结果需满足式(27),才能获得满足KKT 条件的解。
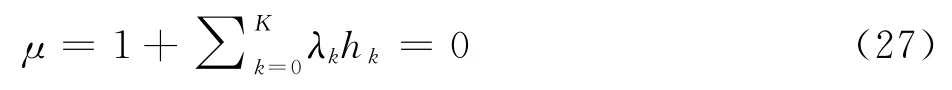
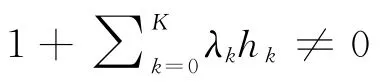
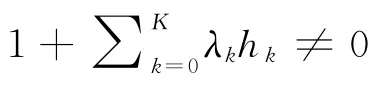
由集群具有统一的飞行时间下边界可得

考虑无人机数量有界,可得
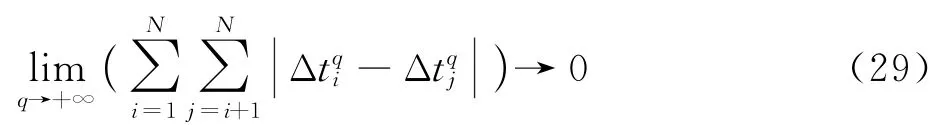
由此可证DPD-SCP能够求解得到满足机间避碰与时间一致约束的集群轨迹。
4 仿真试验结果与分析
本节针对DPD-SCP 开展数值仿真试验,在典型集群编队集结想定下验证DPD-SCP的合理性与时效性。通过对比耦合SCP(cSCP)、串行优先级解耦SCP(spSCP)互换想定,进一步验证DPD-SCP的有效性。针对单机轨迹凸规划子问题P2,使用SeDu Mi与CVX进行求解。基于MATLAB R2017a软件平台进行数值仿真运算,PC机硬件为Intel Core i7-6700 3.40 GHz处理器与8 GB运行内存。
4.1 集群编队想定与参数设置
编队集结想定包含15架无人机,要求集群从分散位置形成雁形编队。无人机初始与终端飞行速度均设置为35 m/s;初始与终端航迹倾角均为0°;初始与终端航向角分别为0°与90°;无人机之间的避碰距离设置为100 m;状态与控制边界约束取值如式(30)所示:
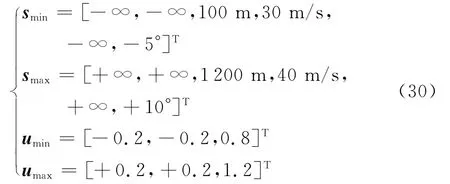
集群编队互换想定包含100架无人机,初始与终端位置等间距分布在半径为3 km 的圆上,初末速度为35 m/s,航迹倾角为0°。想定要求处于对角位置的无人机进行位置互换,初末航向角设置为初始位置朝圆心的方向角。机间安全距离设置为10 m,状态与控制边界如式(30)所示。
使用所提DPD-SCP方法求解编队集结与编队重构轨迹规划问题,轨迹离散数量设置为40。初始信赖域半径、状态收敛阈值、时间一致收敛阈值、优先级调整阈值、飞行时间下边界更新阈值等参数设置如式(31)所示。
cSCP与pdSCP的参数设置分别见文献[11,14],其状态收敛阈值与时间一致收敛阈值同DPD-SCP。
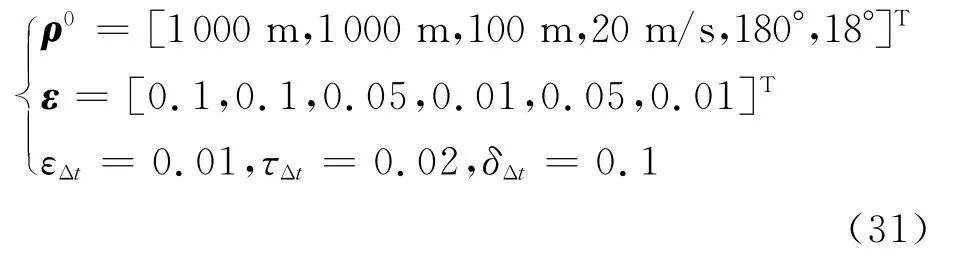
4.2 集群编队集结轨迹规划
4.2.1 编队集结轨迹规划结果
DPD-SCP规划的编队集结轨迹如图5所示。从图中结果可以看出,所生成轨迹能够引导无人机集群从松散编队形成较为紧密的雁形编队,且集群无人机飞行时间均为174.4 s,满足时间一致约束。三维视图与水平投影视图均表明集群飞行轨迹成功规避了环境中的威胁。
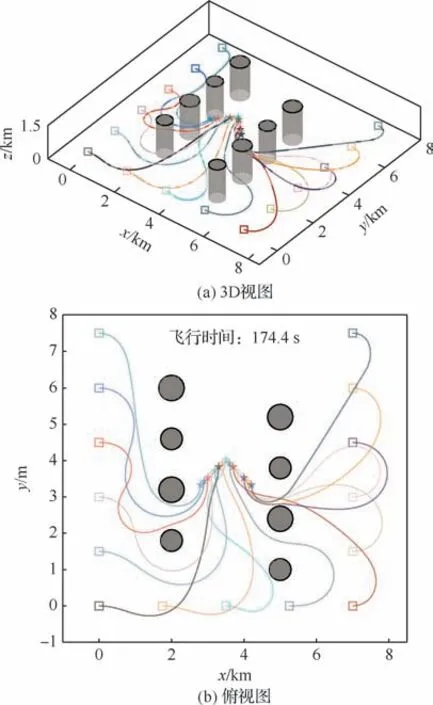
图5 编队集结想定下DPD-SCP的轨迹规划结果Fig.5 Trajectory planning results by DPD-SCP on the formation rendezvous scenario
如图6所示,在编队集结想定下,所生成的集群轨迹满足机间避碰约束,机间最小距离始终大于安全距离限制(100 m),验证了动态优先级解耦机制的有效性。综上分析可得,DPD-SCP方法能够生成满足威胁规避、机间避碰与时间一致约束的飞行轨迹。

图6 编队集结想定下集群轨迹的机间最小距离Fig.6 Minimum distance among UAVs of the swarm trajectories on the formation rendezvous scenario
DPD-SCP分布式求解耗时结果如图7所示,其中图上方标注表示轨迹迭代序列。针对编队集结想定,DPD-SCP通过19次迭代求解得到满足飞行约束与收敛条件的集群轨迹。DPD-SCP 每步轨迹迭代耗时大约为0.5 s。注意的是,每步轨迹迭代耗时取所有无人机当前步迭代耗时的最大值。从结果中可以得出,优先级解耦机制下分布式规划通过并行求解将计算压力分散至每架无人机,增强了方法的可扩展性。
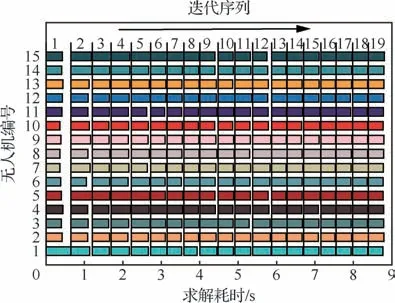
图7 编队集结想定下DPD-SCP分布式求解耗时Fig.7 Runtime of distributed trajectory planning by DPDSCP on the formation rendezvous scenario
4.2.2 编队集结轨迹规划结果对比分析
为充分验证DPD-SCP 方法的有效性,给出不同集群规模编队集结想定下cSCP、spSCP、pdSCP与DPD-SCP目标函数值(飞行时间)对比结果,如图8所示。spSCP包含两层迭代,即外层的协同迭代层和内层的SCP 迭代层。spSCP 在内层迭代收敛后,在外层迭代更新时间下边界约束值,因此spSCP时间下边界值更新存在一定滞后,易于出现时间下边界值迅速增长的情况。pdSCP与DPD-SCP将内外双层迭代合并为一层,在每次轨迹迭代后立即进行时间下边界值调整。因此,相比于spSCP,pdSCP与DPD-SCP能够根据最新的迭代结果更加及时的进行飞行时间调整,避免飞行时间下边界值迅速增长的问题,获得更短的飞行时间。DPD-SCP 的目标函数与cSCP、pdSCP 相当,最大偏差不超过3%,表明DPD-SCP规划结果具有良好的时间最优性。

图8 cSCP、spSCP、pdSCP与DPD-SCP目标函数值Fig.8 Objective function value of cSCP,spSCP,pd-SCP,and DPD-SCP
为进一步验证DPD-SCP 方法的时效性,对比cSCP、spSCP、pdSCP 与DPD-SCP 的规划耗时,如图9所示,其中括号中数据表示迭代次数。由结果可得,DPD-SCP计算效率明显高于cSCP、spSCP与pdSCP,且随着无人机规模增大,DPDSCP效率优势相比于cSCP更加明显。受益于动态优先级解耦机制,DPD-SCP平均迭代次数相比于pdSCP降低了大约15%。15架无人机编队集结想定下,DPD-SCP求解耗时相比cSCP、spSCP与pdSCP 分别减低了93.7%、88.3%与40.2%。综上分析可得,DPD-SCP方法能够降低序列迭代次数,提升轨迹规划方法的收敛速度,相比于其他3种方法具有更高的求解效率与更优的可扩展性。
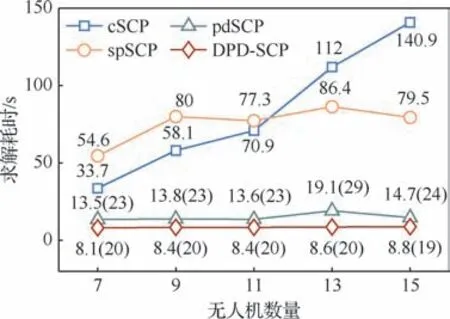
图9 cSCP、spSCP、pdSCP与DPD-SCP求解耗时对比Fig.9 Runtime comparisons among cSCP,spSCP,pdSCP,and DPD-SCP
4.3 集群编队互换轨迹规划
100架无人机编队互换轨迹规划结果如图10所示,机间最小距离如图11所示。针对强耦合的大规模集群轨迹规划问题,DPD-SCP 通过26次迭代规划出满足约束的集群编队互换轨迹,集群飞行时间(目标函数值)为209.8 s。DPD-SCP求解耗时9.9 s,然而对比方法cSCP、spSCP 与pdSCP难以在有限时间内获得可行的大规模集群编队互换轨迹。相比于15架无人机编队集结轨迹规划,100 架无人机轨迹规划耗时仅增加1.1 s,表明DPD-SCP具有良好的可扩展性。
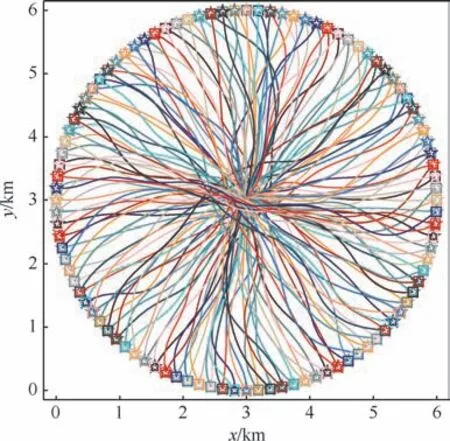
图10 编队互换想定下DPD-SCP的轨迹规划结果Fig.10 Trajectory planning results by DPD-SCP on the formation exchange scenario

图11 编队互换想定下集群轨迹的机间最小距离Fig.11 Minimum distance among UAVs of the swarm trajectories on the formation exchange scenario
5 结 论
1)提出了动态优先级解耦的序列凸规划方法,将集群轨迹规划问题分解为一组单机分布式规划问题,降低了问题维度与求解复杂度。
2)发展了飞行时间驱动的动态优先级解耦机制,根据飞行时间动态调整无人机优先级并更新时间一致约束,提高集群轨迹规划收敛速度。
3)理论分析证明了DPD-SCP能够生成满足碰撞规避与时间一致约束的集群轨迹。数值仿真试验验证了DPD-SCP 的合理性与时效性,结果表明相比于cSCP、spSCP与pdSCP,DPD-SCP具备良好的时间最优性与显著的效率优势。
