基于固-气耦合的不同氧气条件下煤粉点燃数值研究

要华伟，何晓东，王喆

（1.山西焦煤西山煤电集团,山西 太原 030053；2.中煤科工集团沈阳研究院有限公司,辽宁 抚顺 113122）

0 引言

煤炭在当前及未来很长时间内都将是主要的能源之一[1-2]。在很多煤矿工业场景中，煤会以粉尘形式覆盖在不同机械设备上，且在煤运输及储存的环境中也会长期沉积煤尘[3]。在一定条件下，由于设备加热或沉积的煤尘热量积蓄，煤粉会发生突然性着火，进而引发明火燃烧或煤尘爆炸等热动力灾害[4]。

平面热板实验是评价煤粉自热和着火危害最常用的方法，特别适用于煤粉在热表面积聚的情况。文献[5]采用热表面点火实验装置估算了匹兹堡煤着火动力学参数，参数包括导热系数、活化能、反应热和指前因子。文献[6]采用数值模型研究了热边界条件与供氧条件对煤体内温度分布与高温点运移的影响。文献[7]基于有限元软件COMSOL 建立了大型煤堆自燃数值模型，研究了煤堆最易自燃的临界供氧条件和自然发火期等参数。文献[8]基于热板加热实验，采用数值模型研究了锲形热板条件下煤自燃特性，重点考虑了热板温度变化与氧气浓度对煤自燃的温度、气体产物及高温点等特征的影响。文献[9]建立了一种研究煤尘自燃的二维数值方法，重点研究了氧气摩尔分数和稀释气体的作用。

以上文献采用数值方法对热板实验配置下的煤粉着火特性进行了研究，但缺乏对热板实验中煤粉与空气相耦合的煤粉着火特性的数值研究[10-14]，为了能够全面考虑固体和气体耦合条件的煤自燃过程，本文建立了基于固-气耦合条件下煤粉着火的多物理场数值模型，分析了不同氧气体积分数条件下的煤粉着火特征。

1 数值模型

本文采用的热板模型与文献[9]的实验配置相同。选择的煤粉种类是中等挥发分烟煤，煤样的工业分析与元素分析见表1。煤粉平铺在热板表面上，煤的上表面暴露在空气中。在不同温度条件下进行多次实验，当煤中心温度达到450 ℃时，此时热表面的温度为最小点火温度。

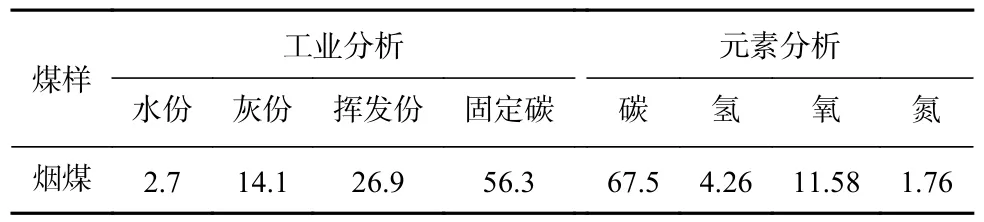
表1 煤样工业分析与元素分析Table 1 The industrial and elemental analyses of coal sample %

煤粉的厚度分别为5，12.5，20，30 mm，直径为100 mm，假设煤粉层边缘为铁制热厚薄层，求解域的气体为空气，初始温度为20 ℃。数值模型采用的煤物理化学参数与文献[9]相同。本文在文献[9]的基础上，不考虑煤氧化反应导致的煤体塌陷及变形，忽略了煤体对气体的吸附及解吸，不考虑煤体中含水率对煤氧化反应影响，对数值方程及边界条件进行修改，并扩展求解域，增加了煤粉附近空气流动域。数值模型中煤粉底部的平板设置为某固定温度，采用平板对其上方的煤粉进行加热。

煤自燃过程能量方程为

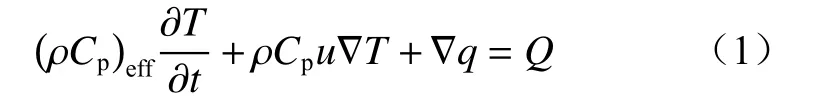
式中：(ρCp)eff为平均有效体积热容，J/（m3·K），ρ为气体密度，kg/m3，Cp为气体恒压比热，J/（kg·K）；T为温度，K；t为时间，s；u为流速矢量，m/s；q为传导热通量，W/m2；Q为煤氧化反应等效热源，W/m3。

煤氧化反应过程释放的热量为

式中：Rc为化学反应速率，mol/（m3·s）；ΔHc为煤样反应热，kJ/kg。

粉层表面热辐射为

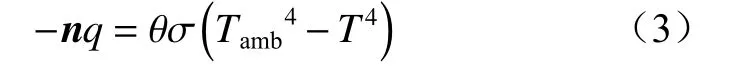
式中：n为轴向矢量；θ为煤体表面辐射度，θ=0.8；σ为Stefan-Boltzmann 常量；Tamb为环境温度，Tamb=293.15 K。

煤自燃过程质量方程与流体流动方程（Brinkman方程）为

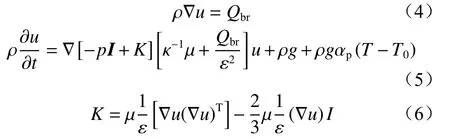
式中：Qbr为质量源，kg/（m3·s）；p为压力，Pa；I为张量矩阵；K为张量函数；κ为渗透深度，m2；µ为动力黏度，kg/（m·s）；ε为煤体孔隙率；g为重力加速度，9.8 m/s2；αp为体积热膨胀系数（1/K）；T0为初始温度，K。

为求解煤氧化反应过程中各种物质产生与消耗，煤自燃过程物质传递方程为

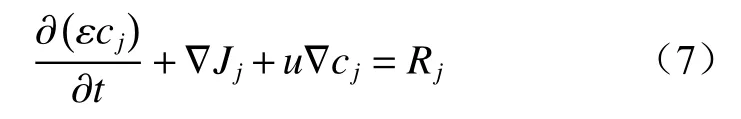
式中：cj为第j种气体浓度，mol/m3；Jj为第j种气体质量通量，kg/（m2·s）；Rj为第j种气体化学反应速率，mol/（m3·s）。

由阿伦尼乌斯定律可得烟煤多相氧化速率。

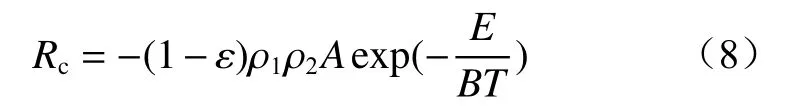
式中：ρ1为 氧气密度，kg/m3；ρ2为煤密度，kg/m3；A为指前因子，m3/（kg·s）；E为煤粉表观活化能，kJ/mol；B为理想气体常数，J/（mol·K）。

2 结果与讨论

2.1 数值模型可靠性验证

为得到准确数值模型结果，对数值模型进行网格及步长无关性检验。煤粉最大温度随时间变化曲线如图1 所示。可看出随着网格数增加，温度的变化趋于一致。当网格数大于5 388 时，计算结果收敛，网格数对模拟结果影响变小，本文采用网格数为5 388。

图1 煤粉最大温度随时间变化曲线Fig.1 Varitation cure of maximum temperature of pulverized coal with time

不同求解步长得到的煤粉最大温度发生失控时对应时间如图2 所示。可看出固定时间步长计算结果随固定时间步长增加出现振荡，而变步长方法计算的结果与较小的固定时间步长计算结果一致，都为37 min。由于变步长方法计算成本较小，本文采用变步长方法进行计算。

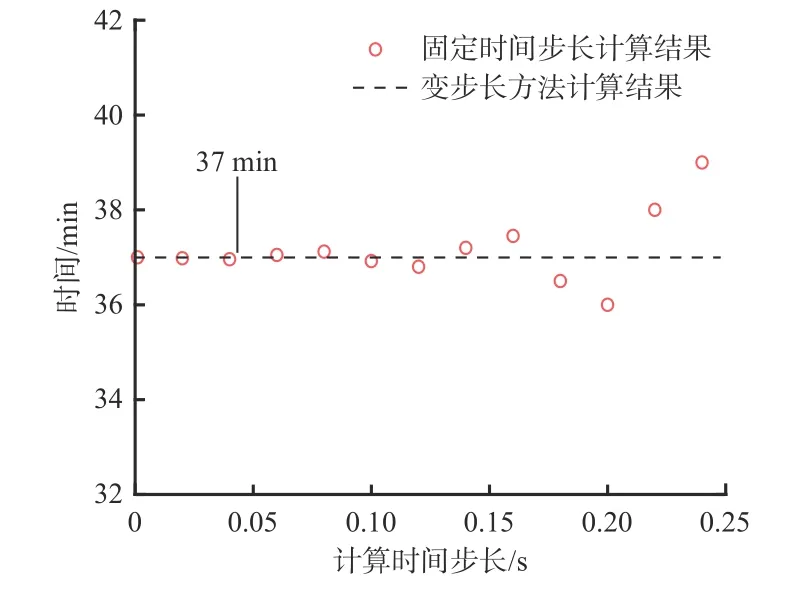
图2 不同求解步长得到的温度失控时间Fig.2 Temperature runaway time obtained by different solving steps

通过文献[9]实验结果验证数值模型的准确性，文献[9]实验结果与数值模型结果对比如图3 所示，其中，Tp为热板温度，℃。烟煤煤粉出现热失控时，对应热板温度为215 ℃，而未出现热失控时，热板温度为210 ℃。对于发生热失控的情况，烟煤煤粉在30 min 之前缓慢升温到170 ℃，在37 min 时突然发生热失控。对于未发生热失控的情况，烟煤煤粉在30 min 后温度变得稳定，温度低于150 ℃。由图3 的热失控及未发生热失控情况的温度分布云图可看出：当发生热失控时，在煤粉中心处出现高温区域，未发生热失控时，不存在明显高温点。表明模拟结果与文献[9]实验结果有较好的一致性，本数值模型的结果是可靠的。

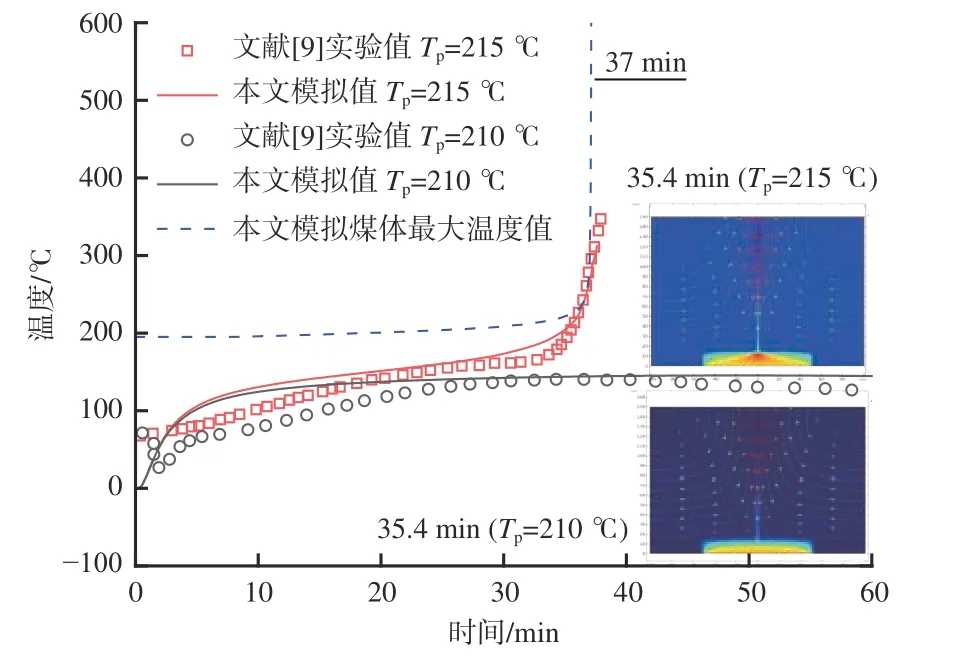
图3 实验温度结果与数值模型结果对比Fig.3 Comparison of experimental temperature and numerical model results

为进一步验证数值模型的准确性，在更厚烟煤煤粉条件下，对数值模型最小点火温度与文献[9]结果进行对比，结果如图4 所示。可看出最小点火温度随烟煤煤粉厚度的增加而减小，这是由于煤粉热储存能力相对增强导致在较低热板温度下煤可自燃。且文献[9]实验结果与数值模型对应的最小点火温度差异较小，证明了数值模型的可靠性。

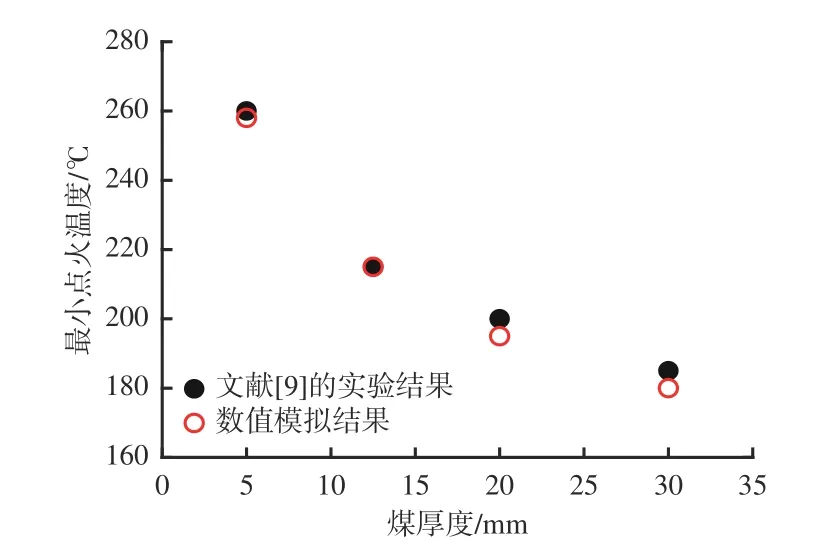
图4 最小点火温度对比Fig.4 Comparison of minimum ignition temperature

2.2 氧气含量对煤自燃特性影响

采用固-气多相耦合多物理场数值模型研究不同氧气体积分数条件下烟煤煤粉自燃特性。不同氧气体积分数条件下煤粉温度变化如图5 所示。可看出不同位置的煤粉温度随时间的增加而升高，煤粉前期温度升高是由于热板热传递导致的；当煤粉最大温度超过热板温度时，由煤粉氧化反应主导；随着煤氧化反应进一步增强，煤粉最大温度达到热失控状态。煤粉内最大温度峰值随氧气体积分数增加而增加，表明氧气含量越高，煤氧化反应越强。此外，初期煤粉温度随测点高度增加而减小，这是由于初期煤升温主要依赖于热板传热，且煤层内部蓄热条件较优。煤粉着火之后测点对应温度随测点高度增加而增加，这表明煤氧化反应主要影响因素由蓄热转变为氧气，而煤粉表面的氧气含量相对较高。

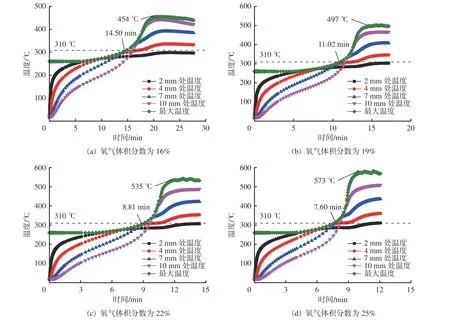
图5 不同氧气体积分数条件下煤粉温度变化Fig.5 Temperature changes of pulverized coal under different oxygen volume fraction

点火延迟时间tIDT与温度峰值Tpeak能够较好地表示煤自燃特征，点火延迟时间和温度峰值与氧气体积分数的关系如图6 所示。可看出点火延迟时间随氧气体积分数增加而减小，温度峰值随氧气体积分数增加而增大。

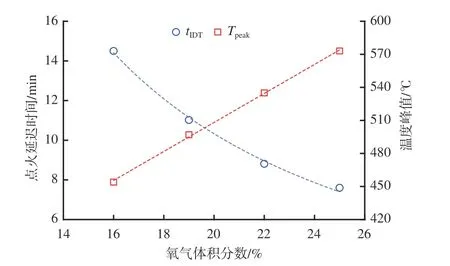
图6 点火延迟时间和温度峰值与氧气体积分数的关系Fig.6 The relationship between ignition delay time and temperature peak and oxygen volume fraction

Tpeak与氧气体积分数的线性关系为

式中：x为氧气体积分数，%；a，b为拟合常数。

tIDT与氧气体积分数的线性关系为

由式（9）和式（10）可看出，Tpeak随氧气体积分数呈线性增加关系，tIDT随氧气体积分数呈指数减小关系，其对应的拟合优度分别为0.998 56，0.995 31，表明拟合结果是可靠的。

3 结论

（1）烟煤煤粉发生热失控情况时，烟煤煤粉在30 min 之前缓慢升温到170 ℃，在煤粉层中心处出现高温区域，在37 min 时突然发生热失控。烟煤煤粉未发生热失控情况时，煤样在30 min 后温度变得稳定，温度低于150 ℃，不存在明显高温点。模拟结果与文献[9]实验结果有较好的一致性。模拟结果与文献[9]实验结果最小点火温度随烟煤煤粉厚度的增加而减小，且对应的最小点火温度差异较小，证明了数值模型的可靠性。

（2）烟煤煤粉前期温升是由于热板热传递导致的，随着烟煤煤粉温度增加，煤氧化反应主导因素由热量转变为氧气。

（3）初期煤粉温度随测点高度增加而减小，煤粉着火之后测点对应温度随测点高度增加而增加。

（4）点火延迟时间随氧气体积分数增加而减小，温度峰值随氧气体积分数增加而增大。