基于混沌时间序列的资源管理大数据挖掘方法

杨 斐

(阜阳职业技术学院 工程科技学院，安徽 阜阳 236031)

0 引 言

在现代国民经济发展中，数据挖掘的地位与重要性日益增强，在民用及军用方面均取得了不俗的成效，为人们的生活提供了诸多便利[1-3]。根据混沌系统对原始值较为敏感的特点，可将输入资源管理信号的细小变化都迅速呈现在输出信号内，反映出信号的真实状况[4]。混沌时间序列根据其内部的确定性规律，可以对目标进行精准预判，在经济预测、地震勘测等诸多领域发挥了重要作用。

由此，本文提出一种基于混沌时间序列的资源管理大数据挖掘方法。其创新之处在于依据混沌时间序列模型，找到预测点的相邻同向转换形态及其后续时间序列的函数关联，完成对被测目标位置的正确预判；其关键在于，在保持信号稳定性的情况下，利用基于峰值点修正的资源管理大数据挖掘方法，降低挖掘偏差几率，最大限度提升挖掘的精准度，使其广泛使用在各个领域。

1 混沌时间序列模型构建

为了提升资源管理大数据挖掘的挖掘效率，本文使用混沌时间序列模型对被测资源区域位置采取精准预测，达到减少挖掘误差的目的[5-7]。

可将混沌时间序列当作某一时间参变量获得的动力系统解析式：

X=f(x)

(1)

其中，f(x)表示反映动力系统伴随时间推移的函数关系式。

按照混沌及分形原则，可获取具备n个形态参变量xi随着时间推移的非线性动力系统，具体的控制方程可描述为

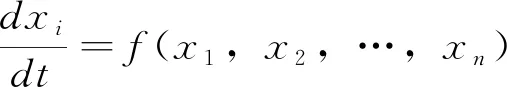
(2)

对于离散状态的管理时间序列而言，可使用不持续时序x(t)及其在(n-1)时滞的管理信息，共同组合为动力轨迹：

x(t)=(x(ti),x(ti+τ),…，x(ti+(n-1)τ))

(3)

利用此种手段把数据的固有时间进行推迟，重新建立一个等价的多维状态空间，反复此过程得到不同时段的推迟数量，可生成一个在n维相空间的相点演变路线。在进行演算时，要把初始管理数据{xi}根据相应的时间间隙τ(τ=k*Δt)扩充成n维空间的相型分布。因此，将时间序列的相空间描述成：

xi(t)=(x(ti),x(ti+τ),…，x(ti+(m-1)τ))

(4)

(4)中的相位分布包含m个相位点，每个相位点都包含n个分量。相位点之间的线段表示系统在n维空间中的演化。

相空间的混沌吸引子具备一定的平稳性及分形性，通过寻找预测点的相邻同向转换形态和其后续时间序列的函数关联，以此完成对目标资源的区域位置判断。与此同时，因为相邻的每个状态点与预测点的空间大数据是不相等的，所以对预测的影响也不相同[8-9]。由此，本文提出一种基于邻近点权重的混沌时间序列模型。

若与X(t)大数据待挖掘点最近的点为Xr(t)，r=1,2,…,n， 且相应点至预测点X(t)的间距是dr， 将dr中的最小值设置成dmin，那么第r个相邻点权重为

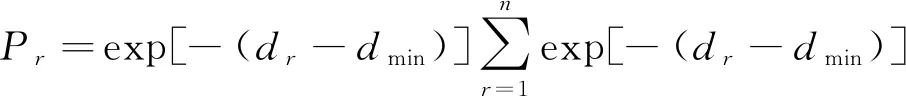
(5)

想要完成在X(t)领域中采取下一步预测，可利用式(6)的演变关联得到下一个预测数值。

Φ[X(t)]=(Φ1(X),Φ2(X),…,Φm+1(X))T=(1,x(τ),x(t-τ),x(t-2τ),…,x(t-mτ+τ))T

(6)

X(t)每个相邻点在t+τ时段会演变成Xr(t+τ)， 使用加权最小二乘法将其进行最小化，具体表示为

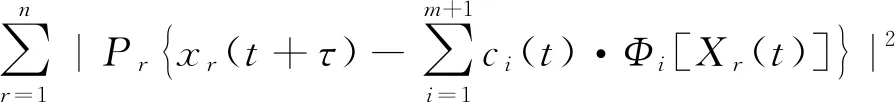
(7)

2 资源管理大数据回波信号去噪

资源管理大数据挖掘的流程通常是将待测目标资源输入到资源管理模式中，进行样本采集，用触动发射机的时间挖掘系统开始计时[10-11]，生成信号后终止计时，然后按照管理流程推算出目标大数据，具体运算方程为

D=c×t/2

(8)

其中，D表示探测器至探测目标的间距，t表示资源管理模式迭代消耗的时间，c表示管理流程代号，为常数。在资源管理过程中向平台云服务器射出资源管理模式信号后，其反射的回波信号强度会伴随大数据的减少产生平方衰减，信号会产生大的噪声，严重影响挖掘结果的精确度，因此，对回波信号进行去噪是极其重要的。

根据经验模式分解(empirical mode decomposition,EMD)，可以自适应地将信号分解成有限个IMF，其中每个IMF分量都是一个振荡信号x(n)， 包含初始信号的频率分量的一个子集。最小二乘法应遵循两个原则：①极值点数与过零点数必须相等,②由极值点决定的上下包络平均值必须等于0。

经验模态分解对IMFs的提取过程就是一个择优挑选的过程，最后就会得到IMFs与残差相加的初始信号：

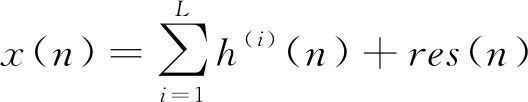
(9)

其中，h(i)(n)表示第i个IMF分量，L表示获得的IMFs数量，res(n)表示残差。

在已知实际信号y(n)的前提下，对其引入噪声信号e(n)， 则引入噪声后的信号可描述为

x(n)=y(n)+e(n)

(10)

针对传统EMD去噪手段，其原理是把包含可用信号的有关分量采取重构，具体表示为

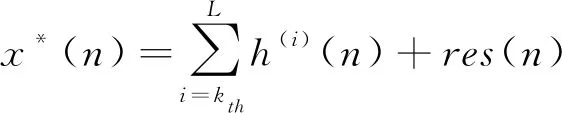
(11)

其中，kth的取值取决于根据初始信号x(n)和IMF分量之间的关联性。也可将重构后的信号描述为

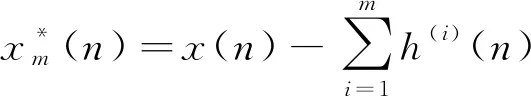
(12)

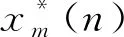
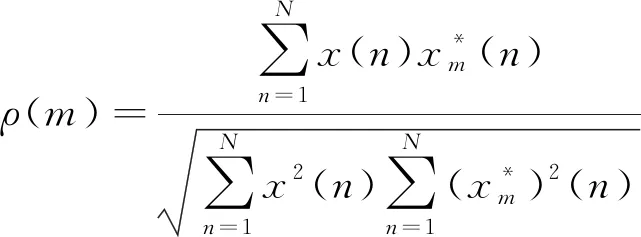
(13)

其中，N表示IMF分量长短，m是ρ(m)初始阶段不大于常数C时的相对值。ρ(m)的值逐步变小，直到变成一个最小值，利用C值的确定，可以判断出kth的所处范围，也就是第一个关联分量范围：

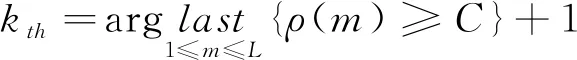
(14)

其中，last为ρ(m)内最后一个大于等于C的值，C值的择取范围是[0.55,0.65]，本文将C值选定位0.65，L表示IMF分量数目。

经过上面的步骤就能够得到kth的具体位置，把前kth-1项IMFs当作互不关联分量，则其余IMFs就是关联分量。

当干扰强度较大时，用EMD分解后向散射信号，将信号与噪声分离到相同的IMF分量。可靠的信号经常在使用emd-d去噪时被忽略。利用软阈值对不相关分量进行处理，得到可靠的隐藏信号，处理流程如式(15)。

(15)

其中，h(i)(n)表示第i个IMF分量，Ti表示临界值，具体描述为

(16)

其中，N表示IMF分量的长短。

针对关联分量，本文通过粗糙惩罚对其采取平滑处理。使用粗糙惩罚的目的是解决最小二乘法计算的不稳定性，其根本原理就是在最小二乘法的基础上引入惩罚项当作光滑模型

(17)

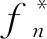
粗糙惩罚的主要功能是控制拟合函数的平滑度，使拟合结果在不损失真实数据的情况下保持稳定。这既能增强回波信号的平滑性，又能防止信号失真，极大地提高了资源管理中数据挖掘数据的真实性。

3 基于峰值点修正的资源管理大数据挖掘方法

平台云服务器的资源管理大数据信号是对称sinc函数波形，其波峰位置不会产生移动，因此只要找到波峰的所在位置，按照发射与接收信号的时间间隔就能得到被测目标的大数据。为了进一步缩小挖掘偏差，保证挖掘结果的精确度，本文利用指数函数修正sinc函数的方法来改善寻峰精度，具体可描述为

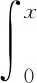
(18)

其中

r(x)=A·sinc(Bx)

(19)

(20)

(21)

(22)

(23)

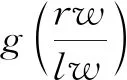
按照接收回波的非对称原则，将修正函数描述为

(24)

其中，τ′是修正常量，AL、AR依次表示将τB作为回波峰值点的左半峰和右半峰面积，通过sinc函数回波模型可进行如下推理：

σ=ΔτB
Wd=2ΔτB

(25)

其中ΔτB是回波的-3 dB带宽。将式(25)引入式(21)～式(23)，可获得如下关系式：

(26)

探寻峰值的精准位置关键在于峰值原始定位及峰值补偿纠正两方面。首先使用多迭代下的累计方法，把每个帧回波按照主波的发射时间对应累加，获得一个全新的迭代信号P(i)，同时将该信号剔除噪声，存留实际波峰及噪声引发的伪峰值点，对迭代信号P(i)采用差分求解获得信号c(i)，符合差分信号为0的点就是全部可能的峰值点，对斜率临界值进行设定能够去除伪峰值点。

因为噪声形成的伪峰也符合c(i)等于0的状况，为了达到去除噪声的目的，需将信号c(i)进行高斯滤波处理，然后使用幅度临界值将信号内幅度小的伪峰值点进行过滤剔除。经过上述步骤即可大致断定波峰的具体位置。

进行峰值点补偿纠正，因为峰值点补偿是解决系统振荡的有效手段，也可对温度变化引起的采峰点非线性漂移自动跟踪补偿，所以按照探寻到的波峰位置将信号采取波形重建，推算出波峰左半部分面积AL与右半部分面积AR，同时对比两者的大小，即可依次将两部分波形使用指数修正函数f(x)采取相对的指数修正。具体操作：将τB作为中心，依次求出左半边与右半边波形的面积，选择适当的指数函数，采取波形拟合改正，借此获得纠正后的峰值点位置τP。

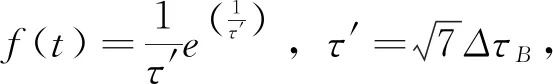
如果AL=AR，就利用sinc函数拟合，获得的τB就是τP的位置；

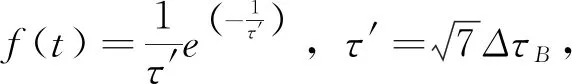
按照修正后获得的峰值点τP所处位置，就能精确推算出云服务平台发射信号与接收间的时间差，以此降低挖掘偏差，使资源管理大数据挖掘的精度最大化。

4 仿真实验

为了验证本文方法的可靠性，在KDNuggets(http://www.kdnuggets.com/datasets/index.html)中，随机选取一个数据集，在保证该数据集可用的情况下，将其作为数据来源，并将本文方法与传统单点资源管理模式挖掘方法进行挖掘精度实验对比，实验平台为MATLAB7.0仿真软件。

想要更为直观地比较两种方法的挖掘精度，下面对其进行挖掘误差对比，具体结果如图1所示。

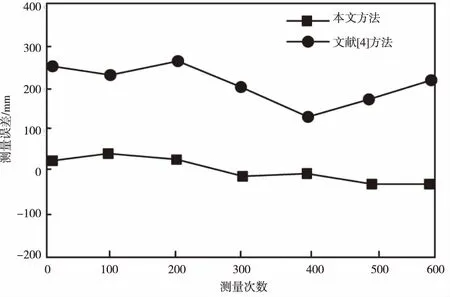
图1 挖掘误差对比

从图1中可以看到，本文方法的挖掘误差较小，具备极高的稳定性，在-50～50 mm波动，而传统方法(文献[4])的挖掘误差波动较大，在100～300 mm波动，且伴随挖掘次数的增加，挖掘误差也随之增多，证明该方法的适用性较差。

5 结 论

为了增强资源管理大数据挖掘的挖掘精度，确保挖掘数据的可用性，本文提出一种基于混沌时间序列的资源管理大数据挖掘方法。首先通过相空间重构及探寻预测点函数关联，构建出混沌时间序列模型，以此预测目标资源的具体方位，为后续的精准挖掘提供先决条件；其次，对资源管理大数据的回波信号采取去噪处理，最大限度减少信号损失，保证信号传输真实性；最后利用基于峰值点修正的资源管理大数据挖掘方法，对回波波形进行拟合纠正，能够更加准确地发现峰值点位置，挖掘误差在-50～50 mm波动，运用幅度临界值把信号中幅度较小的伪峰值点进行过滤剔除，以此提升挖掘精准度，保证挖掘结果的可靠性。