一类二阶线性微分方程的通解及应用

郭 华 毅

(山西药科职业学院，山西 太原 030031)

1 引 入

微分方程是数学的重要分支，研究它的解很有现实意义。对于二阶线性微分方程

y″+p(x)y′+q(x)y=f(x)

其中p(x),q(x),f(x)是关于x的连续函数[1]，求其通解没有一个统一的方法，只是当p(x),q(x)为常数且f(x)=0时，其方程称为二阶线性常系数齐次微分方程，有统一的求通解的方法；当p(x),q(x)为常数，f(x)为几种特殊形式时，也有求通解的方法，待定系数法；对于其他的形式，并没有统一的求解方法，所以对于更一般的二阶线性微分方程解的计算[2-3]，是值得研究的问题。

常数变易法是解一阶线性微分方程的方法，下面用类比的方法，猜想二阶线性微分方程解的特点。结合一阶线性齐次微分方程解的结构，猜想二阶线性齐次微分方程解也有形如其解的形式。

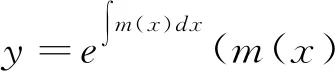
y″+p(x)y′+q(x)y=0

的特解，则

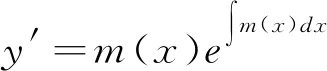
将y′和y″代入方程y″+p(x)y′+q(x)y=0，整理，得m′(x)+m2(x)+p(x)m(x)+q(x)=0。

2 定理及证明

定理1 对于二阶线性齐次微分方程y″+p(x)y′+q(x)y=0， 若存在函数m(x)， 使得m′(x)+m2(x)+p(x)m(x)+q(x)=0成立， 则方程y″+p(x)y′+q(x)y=0的通解为

分析 对于方程y″+p(x)y′+q(x)y=0的通解问题， 只需要找到方程y″+p(x)y′+q(x)y=0的两个线性无关的特解即可。

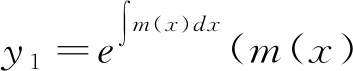
令y2=n(x)y1为待定函数， 且n(x)非常数是y″+p(x)y′+q(x)y=0的另一个特解， 显然y1和y2线性无关。

求导，得

y2′=n′(x)y1+n(x)y1′=[n′(x)+m(x)n(x)]y1

y2″=[n″(x)y1+m′(x)n(x)+m(x)n′(x)]y1+[n′(x)+m(x)n(x)]y′

=[n″(x)y1+m′(x)n(x)+2m(x)n′(x)+m2(x)n(x)]y1

将y2′和y2″代入方程y″+p(x)y′+q(x)y=0， 整理， 得到[n″(x)+2m(x)n′(x)+p(x)n′(x)+(m′(x)+m2(x)+p(x)m(x)+q(x))]y1=0。

已知m′(x)+m2(x)+p(x)m(x)+q(x)=0且y1≠0， 故n″(x)+2m(x)n′(x)+p(x)n′(x)=0。

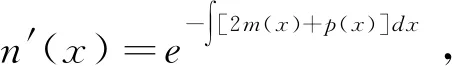
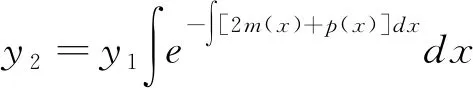
方程y″+p(x)y′+q(x)y=0的通解为y=c1y1+c2y2， 将上边所求的y1和y2代入， 有

即所求的二阶线性齐次微分方程y″+p(x)y′+q(x)y=0的通解。

定理证毕。

定理2 对于二阶线性非齐次微分方程y″+p(x)y′+q(x)y=f(x)， 若存在函数m(x)， 使得m′(x)+m2(x)+p(x)m(x)+q(x)=0成立， 则方程y″+p(x)y′+q(x)y=f(x)的通解为

y′=k′(x)y1+k(x)y1′=[k′(x)+m(x)k(x)]y1
y″=[k1″(x)y1+m′(x)k(x)+m(x)k′(x)]y1+[k′(x)+m(x)k(x)]y′
=[k″(x)y1+m′(x)k(x)+2m(x)k′(x)+m2(x)k(x)]y1

将y′和y″代入方程y″+p(x)y′+q(x)y=f(x)， 整理， 得

[k″(x)y1+2m(x)k′(x)+p(x)k′(x)+(m′(x)+m2(x)+p(x)m(x)+q(x))]y1=f(x)

将m′(x)+m2(x)+p(x)m(x)+q(x)=0代入， 得

显然方程是关于k′(x)的一个一阶线性微分方程，用常数变易法，可求得通解，得

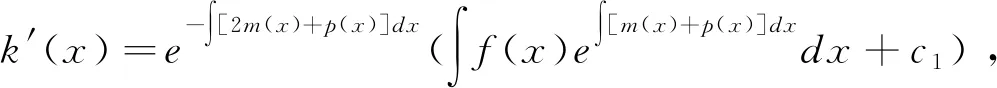
c1,c2是任意常数。所以，有

是二阶线性微分方程y″+p(x)y′+q(x)y=f(x)的解，且该解有2个独立的任意常数，所以该解是二阶微分方程的通解。

定理证毕。

其中定理2求通解的方法，没有按照常规二阶线性非齐次微分方程求通解的定理：先求对应齐次微分方程的通解再加非齐次的特解得到其通解，而是直接根据常数变易法的思路，直接求出一个解，再根据通解的定义，说明求出的这个解刚好又是通解。

注：定理1和定理2所有不定积分常量都选为0。

3 举例应用

例1 求微分方程xy″+2(1-x)y′+(x-2)y=0的通解。

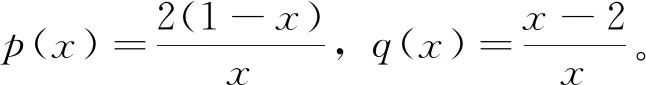
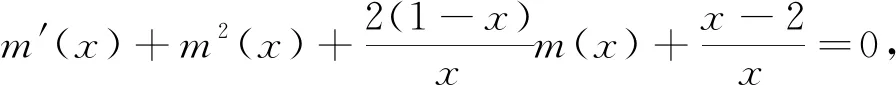
分析 ①这是一个二阶线性变系数微分方程，也可以看成一个欧拉方程，令x=et，就可以将原方程整理为一个二阶线性常系数微分方程；

②也可以利用文献[5]的定理2计算；

③下面用本文的定理2求其通解。

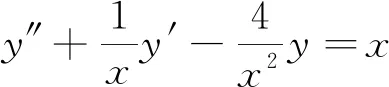
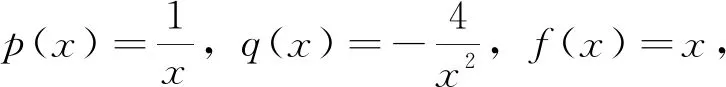
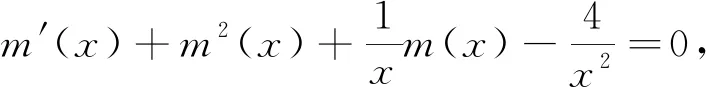
3 结 论

利用上面2个定理的公式求二阶线性微分方程的通解，最关键问题是能找到函数m(x)，使得m′(x)+m2(x)+p(x)m(x)+q(x)=0成立。一般情况下，我们会结合导数的特点，观察验证，从而找到合适的m(x)，这样也使得定理具有局限性；但二阶线性微分方程并没有一个统一的初等解法，利用常数变易法的思想，寻找到这样的解法，在实际的应用中也会给解决问题带来一定的帮助。对微分方程解的计算，会一直探索，寻找更好的方法。