基于人工神经网络的复杂产品模块化数学建模
2022-03-28赵娜
赵 娜
(济源职业技术学院 基础部,河南 济源 459000)
0 引 言
随着人们生活水平的提高、经济全球化和产品多样化的发展,客户需求呈现出多样化和个性化的特点[1]。客户在低成本、高质量和个性化方面的要求已经成为当前制造业共同面临的严峻挑战[2]。模块化是迎接上述挑战的重要途径,基于合理的产品模块化体系,可以快速地组合成满足客户需求的个性化产品[3-4],同时又可以通过通用模块的批量生产和批量管理降低生产和管理成本[5-6]。随着科技的进步和计算机技术的发展,将人工神经网络应用到复杂产品模块化的数学建模中[7]。
为了提高复杂产品的产量、降低复杂产品的生产成本,需要对产品模块化数学建模进行深入地分析和研究[8]。方峻、魏星、赵森森提出了一种产品模块化数学建模方法,首先采用Bootstrap方法建立了可靠寿命置信区间的预测模型;然后以可靠寿命置信区间最小为目标,以试验预算费用为约束建立了仿真的数学建模;最后以某型号武器管体为例,分析了生成模拟退化数据的一般方法,并对管体的退化试验参数进行了优化设计[9]。李佳、段平、吕海洋等人提出了一种基于改进的逐点交叉验证的复杂产品模块化数学建模方法,该方法用改进的逐点交叉验证方法求取产品的最优形态参数,首先从形态参数取值区间内选定初始形态参数,然后从已知点中顺序选出一个点,使用剩下的已知点构建RBF插值模型,计算被取出点处真实值与插值结果的误差,循环多次,累计交叉验证误差,再依次从形态参数取值区间选取下一个值,重复操作,建立形态参数与累计交叉验证误差之间的函数映射关系;最后通过最小化交叉验证误差来获取最佳形态参数[10]。以上两种方法不能有效地对产品模块化数学建模,导致数学建模的效果不佳,本文提出一种基于人工神经的复杂产品模块化数学建模。
1 复杂产品模块化寿命周期曲线
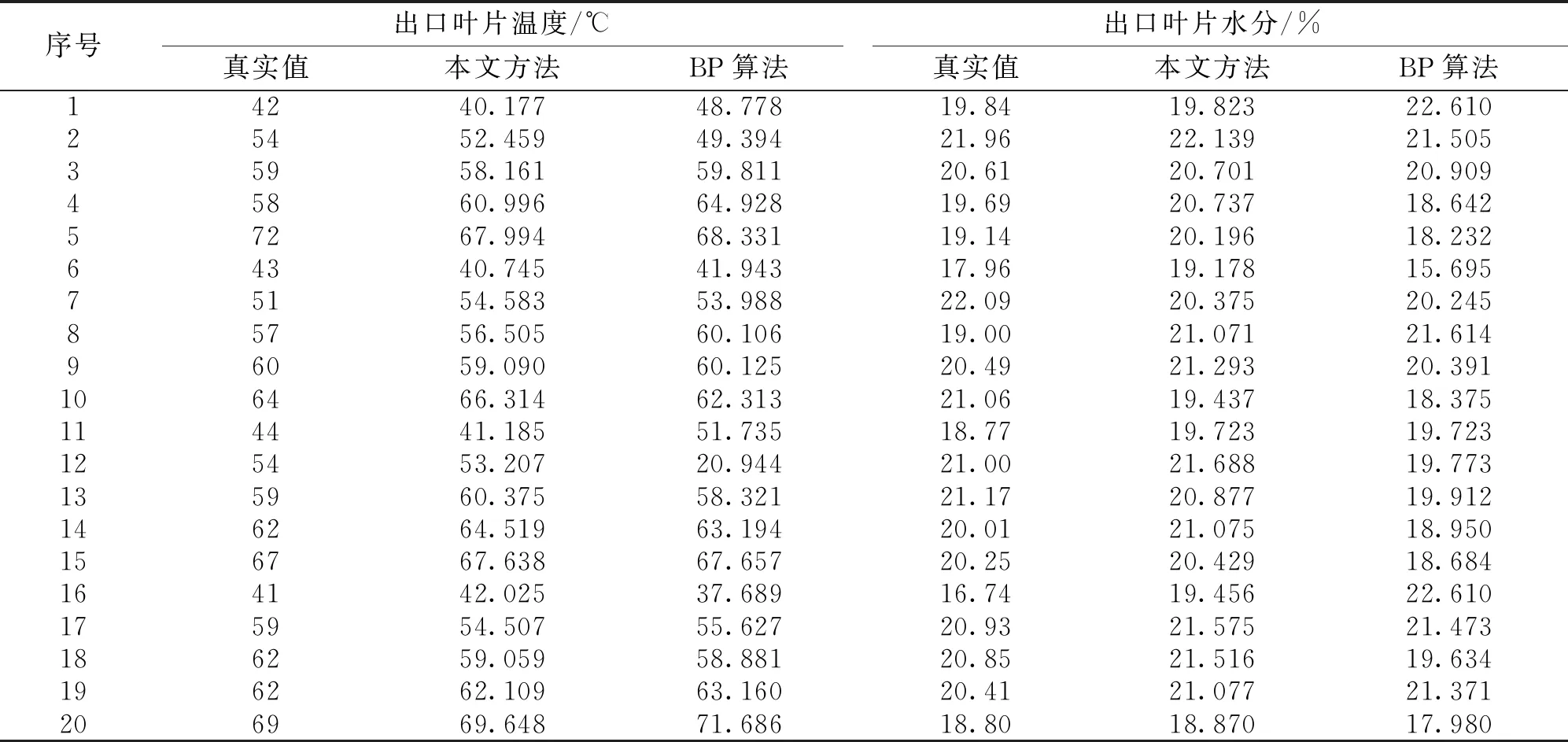
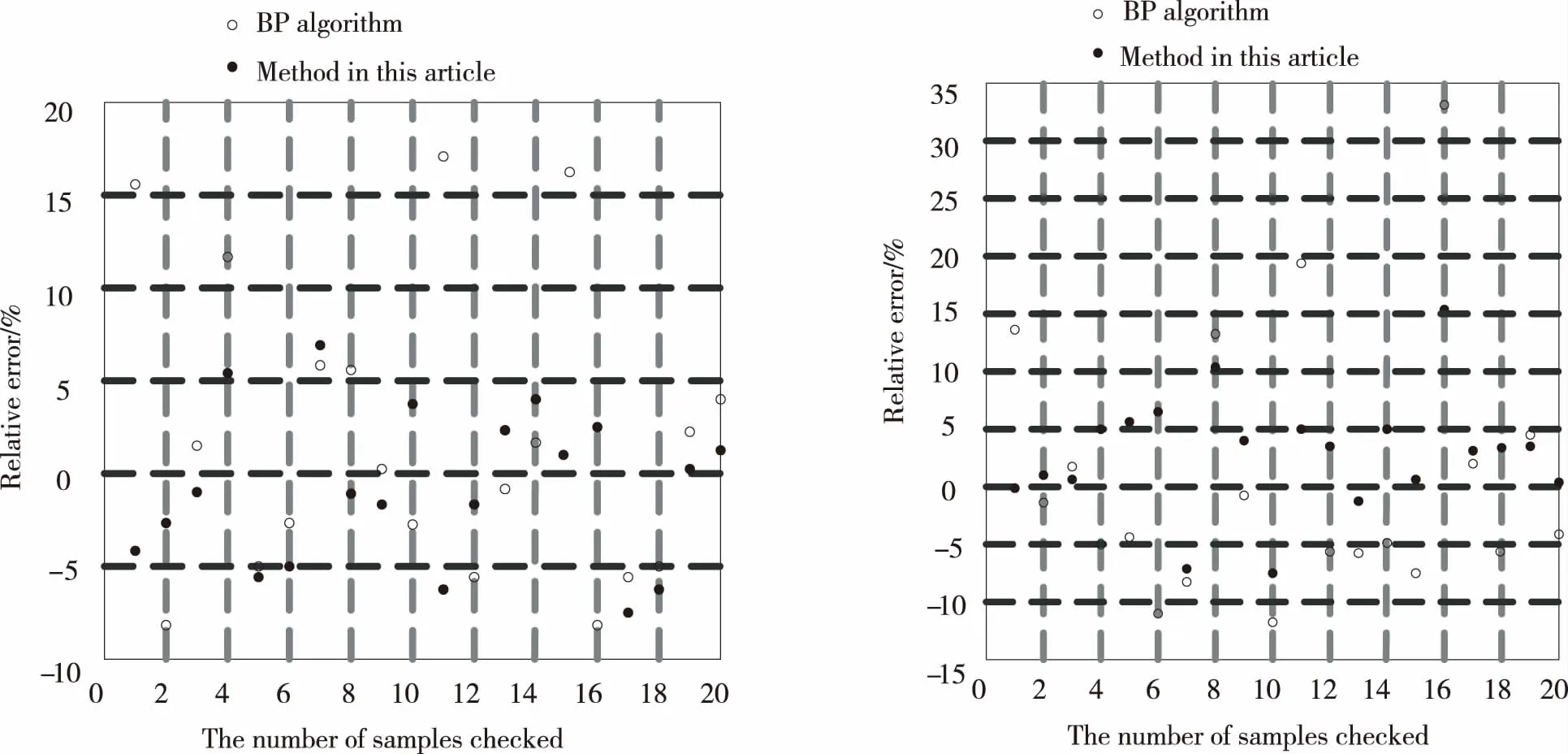
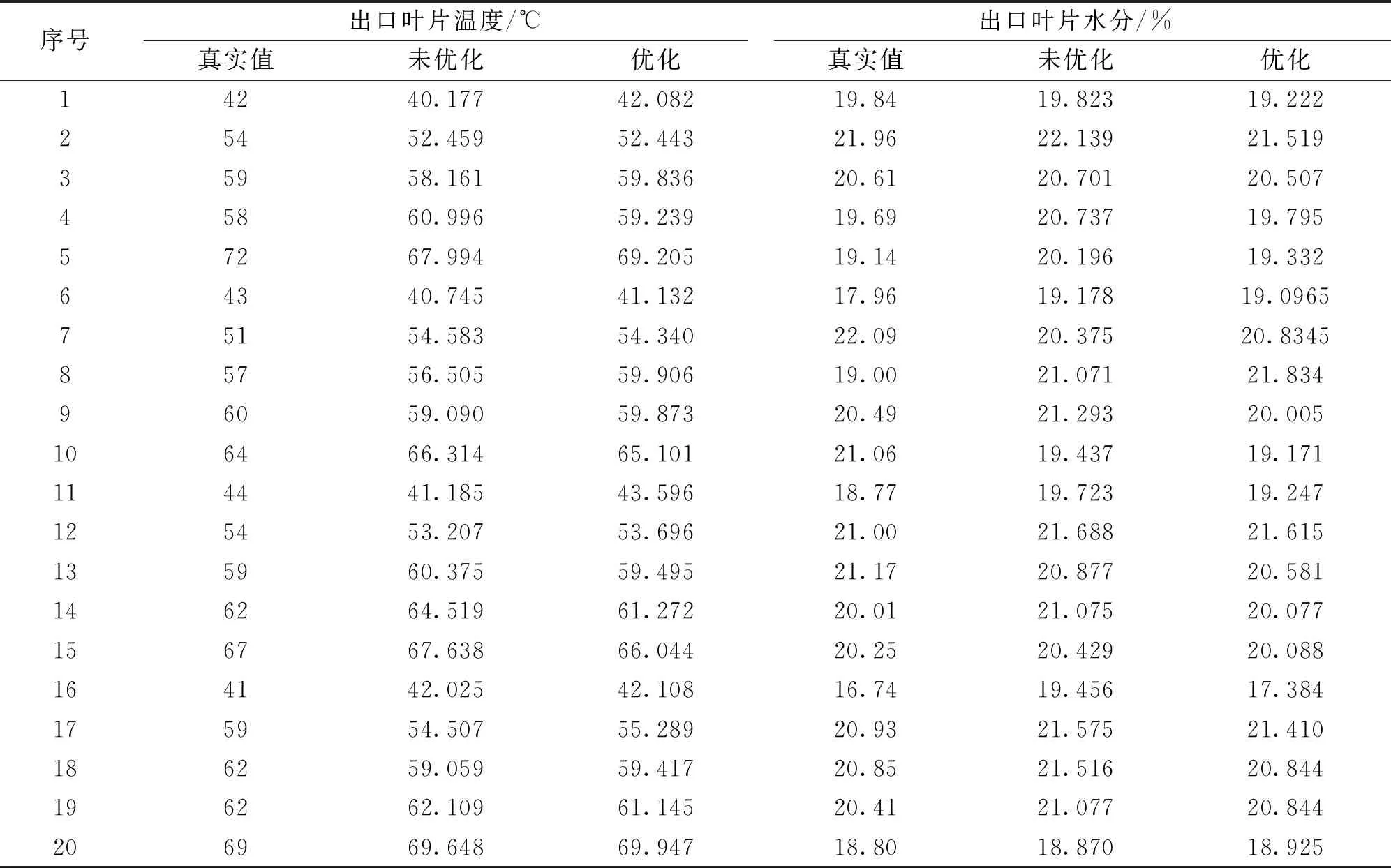
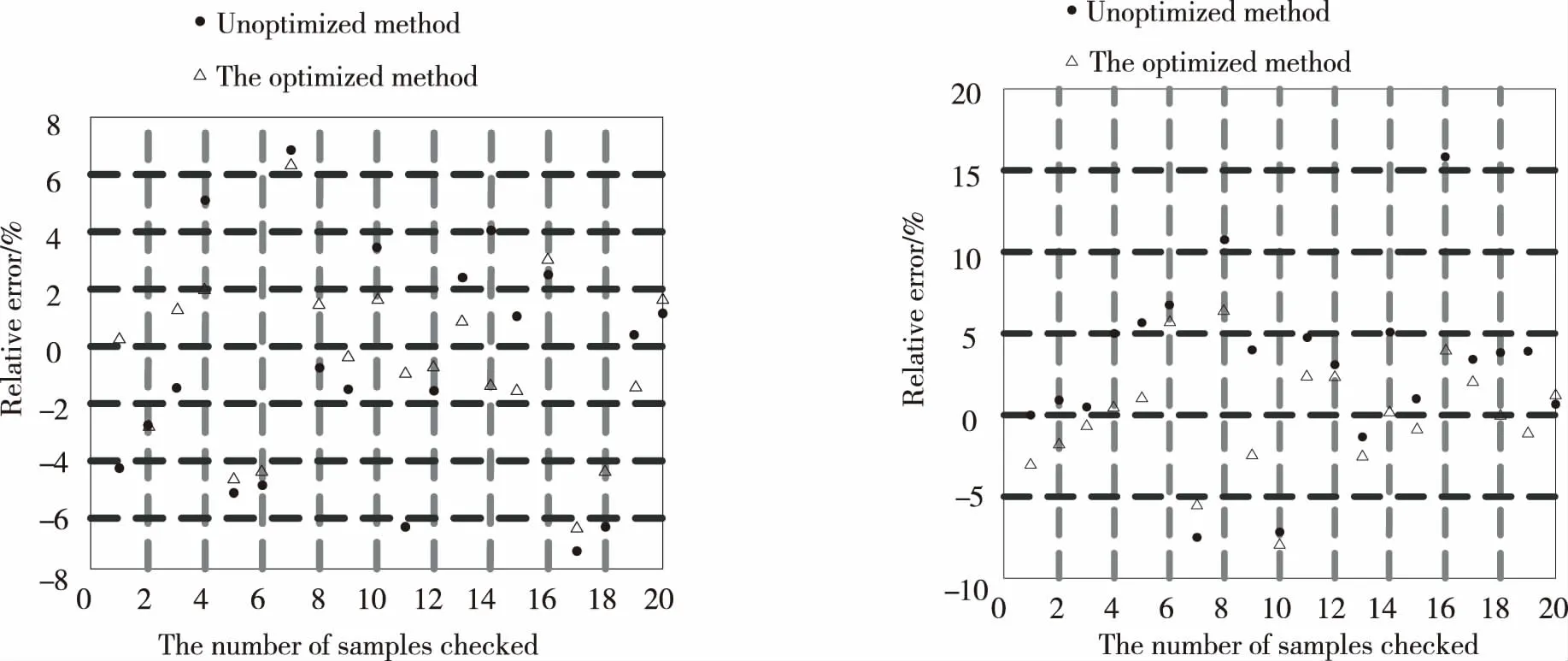
设某复杂产品在一定时间间隔t0 图1 复杂产品的寿命周期曲线 曲线一般划分为4个阶段: ①当t ②当t0 ③当t1 ④当t>t2时,为衰亡期。 对某一种模块化的复杂产品,到ti时的销售总量记为yi, 则 (1) 式中,k为常数。设销售对应的曲线为x=x(t), 则总销售量可表示为 (2) 式中,d代表的是模块化复杂产品的销售速度。复杂产品在成长期,总销量y的增长速度较慢,但由于产品总销量y较小,于是产品销售相对速度1/y、dy/dt较大;将模块化的复杂产品转入畅销阶段,虽然y的增长速度加快,但由于总销量y的迅速增加,相对速度减少;到成熟后期,y的增长明显减慢,相对速度急速减少,并趋向于零。根据以上规律,y(t)应满足以下的微分方程: (3) 其中b,k为待定常数,e代表的是产品的质量解方程,得 y=Le-be-kt (4) 由(2)式解得模块化复杂产品的寿命周期曲线为 x(t)=kbLe-be-kt (5) 其中k,b,L为待定参数,且为正值,由方程(4)得 dy=bkye-ktdt (6) 对公式(6)进行离散处理[12],得到dy=Δy,令dt=Δt=1,公式(6)转变为 Δy=bkye-kt (7) 即 yi-yi-1=bkyie-kti (8) 将公式(8)的两边取对数,令yi-1=0,ui=ln(yi-yi-1)/yi,B=lnbk,得 ui=B-kti (9) 式中,i=0,1,2,…,n,利用一元线性回归分析[13],可得 (10) 其中: (11) 式中,n代表的是复杂产品模块化的数量,u代表的是复杂产品模块化的销售额,在实际计算时,适当地选择ti,当n为偶数时,可使∑ti=0,得到下式 (12) 参数b的计算公式为 (13) 由公式(12)和公式(13)可知,参数k,b可作为已知值,将其代入公式(5)中,利用回归分析法得到下式: L=(∑xi∑bke-kte-kti)-1 (14) 公式(5)中的参数k、b、L可由公式(12)、(13)、(14)确定,当n为奇数时公式(12)、(13)、(14)需要另行计算。 在待定参数k,b,L中,L一般称为增长极限,可由实际问题确定其数值,在此情况下,将L作为已知值,利用回归方法[14],通过公式(4)可以求得参数k,b的表达式为 (15) (16) ui=ln lnL/yi (17) 为了便于计算,在推导(16)、(15)两式时,同样用到∑ti=0,ti-ti-1=1,i=0,1,2,…,n,n为偶数。 1)以最高复杂产品模块化质量为目标的目标函数设计。 通常情况下,与产品质量有关的加工时间主要考虑以下几种。假设复杂产品加工一个零件所需的时间为tw,tw的计算公式为 tw=t0+tm+tctm/T (18) 式中,t0代表的是其他辅助时间,tm代表的是生产复杂产品模块化所需的时间,tc代表的是复杂产品模块化生产的时间间隔,T代表的是复杂产品模块化的保质期。 (19) 式中,D代表的是产品的直径,m、y、g、q为复杂产品的寿命系数。以最高复杂产品模块化质量为目标的目标函数为 (20) 2)以最低成本(单件产品所用的平均最低加工成本)为目标函数。 单件产品一般平均加工成本C的计算公式为 (21) 以最低成本为目标的目标函数为 (22) 3)以最大利润率为目标函数。 复杂产品模块化平均利润pr的计算公式为 (23) 最大利润的目标函数为 (24) 统一目标法的实质就是将各个复杂产品模块化的目标函数f1(x),f2(x),f3(x),…,fn(x)统一到一个总的目标函数F(x)中: F(x)=f(f1(x),f2(x),f3(x),…,fn(x)) (25) 统一目标法是把多目标函数的问题转变为多个单目标函数的问题来求解[15]。为了调节复杂产品模块化各个目标函数之间的相互关系,给各个目标函数之间引入加权因子w1、w2、…、wq,即采用线性加权组合法,用一个总的目标函数来表示多个目标函数的加权之和。加入加权因子之后,复杂产品模块化的统一目标函数则表示为 (26) 公式(26)中wi是第i项的加权因子,加权因子是一个非负的系数。 建立多目标函数时选取的加权因子分别为t*、C*、pr*,它们分别是相对应的单目标函数优化值的倒数,3个目标函数值所占比例之和为1。 针对复杂产品模块化的零件,在进行人工神经网络应用时,对加权因子进行处理[16-17]。在建立目标函数时,将单目标函数值作为变量,在每代优化中,各个单目标函数都会产生相应的单目标函数值,并将得到的值的倒数带入多目标函数中进行这一代多目标函数值的计算,进行寻优,线性加权后的目标函数为 (27) 1)质量提升约束条件 假设复杂产品模块化的小零件质量提升速度为Vc,提升复杂产品模块化质量机器的主轴转速为g1(x1,x2,x3)≪0,复杂产品模块化质量提升的速度满足机器转速的约束nmin≤n≤nmax,即 (28) (29) 式中,nmin代表的是复杂产品模块化最低的质量提升速度,nmax代表的是复杂产品模块化最高的质量提升速度。 2)复杂产品模块化销售额提升速度的约束条件 销售额提升速度g2(x1,x2,x3),满足速度约束vfmin≤v≤vfmax,即: (30) (31) 式中,vfmin为复杂产品模块化最小的销售额提升速度;vfmax为复杂产品模块化最大的销售额提升速度。 3)复杂产品模块化销售速度约束条件 复杂产品模块化销售速度g3(x1,x2,x3)应满足: (32) 式中,Pmax为复杂产品模块化最大销售速度,Fc为复杂产品模块化的销售数量,η为复杂产品模块化销售数量的有效系数。 以上约束归结为在满足约束的条件下,求目标函数的最小值。 (33) 本文选取长沙卷烟厂工艺研究室2015年7月21日-2016年6月30日的特色二次烟叶进行实验,共有100组样本。每组样本是在不同条件下获得的,前80组作为训练集,后20组作为测试集。分别采用本文方法和BP算法,建立二次烟叶出口物料质量指标参数曲线模型。采用两种不同方法对后20组测试集出口物料质量指标参数进行识别,结果见表1。 表1 两种不同方法的测试结果 为方便比较,对两种方法识别得到的参数绝对误差进行统计(表2);同时,以检验样本数为横坐标,相对误差为纵坐标,得到的数据相对误差分布,如图2~3所示。 表2 两种不同方法识别得到的数据相对误差 图2 两种方法出口叶片温度的相对误差 图3 两种不同方法的出口叶片水分相对误差 实验结果表明,本文方法得到的数据明显比BP算法识别得到的数据更接近真实值。 1)从绝对误差分布情况可知,本文方法得到的数据相对误差都小于BP算法得到的数据绝对误差; 2)本文方法的最大绝对误差(温度:4.491 ℃,水分:2.715%) 3)本文方法得到的数据相对误差,除样本8和样本16的出口叶片水分分别达到:+10.35%和+15.30%,其余样本均在-10%~10%,而BP算法得到的数据相对误差很多都超过了10%,如样本16的出口叶片水分甚至超过了30%。 这是因为本文方法用人工神经网络及线性加权组合法对复杂产品的数学模型进行求解,寻求复杂产品模块化的最优值。证明本文方法对复杂产品模块化数据进行建模较为准确。 由上述实验可知,本文方法尽管优于传统BP算法,但在局部样本上做得还不够完善,与实际情况还存在一些较小的误差。采用基于人工神经网络的复杂产品模块化数学建模对得到的数据进行优化,并对二次烟叶出口物料质量指标重新进行识别,并与上述实验中的结果进行对比。 采用优化后的方法和未优化方法识别后20组测试集出口物料质量指标见表3。为方便比较,对优化前后方法识别得到的数据绝对误差进行统计(表4)。同时,以检验样本数为横坐标,相对误差为纵坐标,描绘识别得到的数据相对误差分布,如图4~5所示。 表3 优化前后识别得到的数据结果对比 表4 优化前后的绝对误差 图4 优化前后的出口叶片温度的相对误差 图5 优化前后的出口叶片水分的相对误差 实验结果表明,优化后识别得到的数据明显比未优化识别得到的数据更接近真实值。 1)从绝对误差分布情况可知,优化后识别得到的数据绝对误差都小于未优化识别得到的数据绝对误差; 2)优化后得到的数据结果最大绝对误差(温度:3.793 ℃,水分:1.888%)小于未优化得到的数据最大绝对误差(温度:4.491 ℃,水分:2.715%); 3)如前所述,未优化前识别得到的数据相对误差一般在-10%~10%,特别是样本8和样本16的出口叶片水分分别达到:+10.35%和+15.30%,而优化后识别得到的数据相对误差一般在-6%~6%(除样本7和样本17的出口叶片温度,样本8和样本10的出口叶片水分,但都没有超过±10%),数据精度有较大改善。 验证结果证明基于人工神经网络的复杂产品模块化数学建模方法较为有效。 对复杂产品模块化数学建模,具有降低生产、管理成本和提高产品质量的作用,传统方法对产品模块化的数据进行建模时,不能准确地识别复杂产品中的数据,导致不能有效地完成复杂产品模块化数学建模研究。本文提出一种基于人工神经网络的复杂产品模块化数学建模研究,通过实验证明,本文方法可以有效地对复杂产品模块化的数据进行识别,完成复杂产品模块化数学建模研究。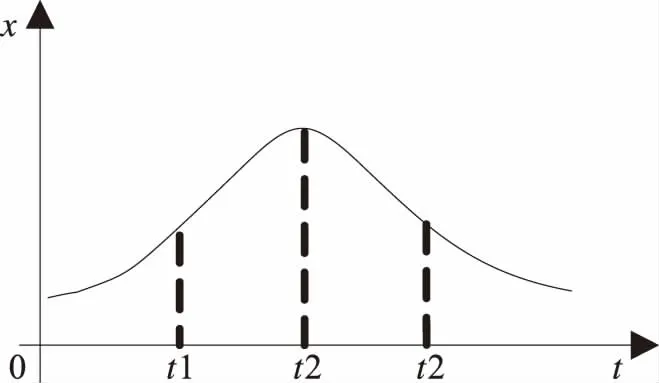
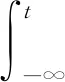
2 基于人工神经网络的产品模块化数学模型构建
2.1 数学模型构建
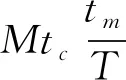
2.2 多目标函数
2.3 约束条件处理
4 实验结果与分析


5 结束语
