利用基因表达谱数据进行各基因相互关系的数学建模方法
2022-03-28鲍芳
鲍 芳
(太原学院数学系,山西 阳泉 030031)
在系统生物学领域,基因网络是基因组机理与功能分析的基础模型,研究者们通常利用基因对谱数据进行描述并创建逆向网络[1-3]。本文采用系统生成谱数据的逻辑分析(LAPP)方法,依据多个基因描述谱数据,采用信息熵的逻辑分析方法来找寻多个基因之间的逻辑关系,并基于多个基因之间所存在的一阶与二阶逻辑关系来确定不同变量的函数关系,进而生成复杂的基因逻辑网络,对目标的逻辑关系进行描述,从而在数量和基因清除率方面获取清晰的表述。
1 基本理论概述
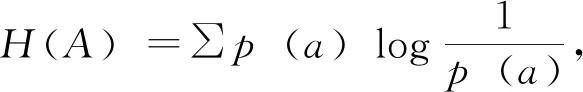
一阶逻辑和二阶逻辑的具体定义为,在不同环境中对基因A的表达量进行N次测量,将得到的数据归一化并构建一个N维向量,称之为基因A的描述谱。基因A与基因B的描述谱中的第n个元素分别为an、bn,A∩B向量中的第n个元素为an∩bn,A∪B向量中的第n个元素为an∪bn,基因﹁A向量中的第n个元素分别为﹁an,an∩bn:=min{an,bn},an∪bn:=max{an,bn},﹁an:=1-an。在此基础上,一阶逻辑关系的函数表达式为f(A)=A,f(﹁A)=﹁A。二阶逻辑关系函数g(n)(n=1,2,…,10)的表达式见表1。

表1 二阶逻辑关系函数表达式
微分方程模型能够清晰地描述各基因表达量之间的逻辑关系,进而使研究者更为清晰地了解基因清除率和表达量数量关系所产生的影响。所以需要基于LAPP方法,依据不同基因的一阶、二阶逻辑关系确定变量间的函数关系。由此,如果基因A到基因B具有f1(A)→B的逻辑关系,那么就能够用f1(x)=x表征A与B的数量关系,而对于一阶逻辑f2(A)→B则通过f2(x)=1-x来描述。二阶逻辑的函数关系见表2(x,y,z分别代表A,B,C三个基因的表达量)。
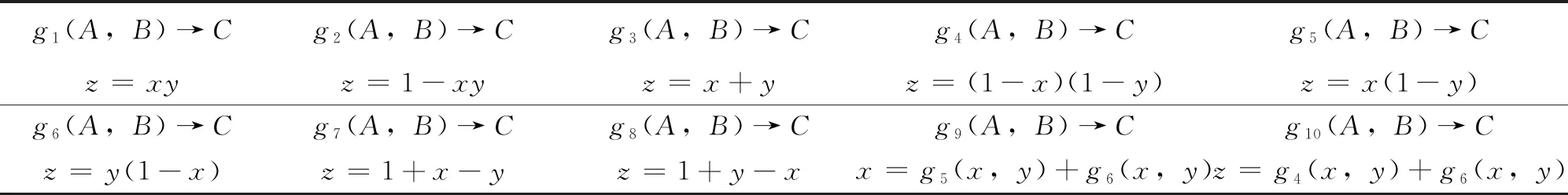
表2 二阶逻辑的函数关系
2 样本采集与模型的建立
国外从事系统生物学研究的EBI(欧洲生物信息研究所)与NCBI(美国生物技术研究中心)都建立了包含大量实验数据的生物学基因测量与分析数据库,其中NCBI数据库中的GSE11452样本集中保存了大量酿酒酵母菌基因行为描述的实验数据。本文从该数据库中进行数据样本的选取,用以研究有氧与无氧环境切换时基因与酿酒酵母菌的逻辑关系。有氧环境下的基因样本组成1号实验组,无氧环境下的基因样本组成2号实验组,依据两种环境下基因描述的不同从大量的数据中选取出4个酵母菌呼吸作用相关的关键基因,分别为9176_at(文中代号A)、4672_at(代号B)、8053_at(代号C)、11432_at(代号D),这些基因的作用主要体现在跨膜功能的描述和线粒体呼吸机理的产生。
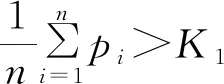
从4个关键基因中选取在有氧和无氧环境下与上述两个具有最大差异的基因同时存在二阶逻辑关系的基因,通过计算所获取的结果为8053_at(C)和11432_at(D)。
在无氧和有氧环境中4个关键基因之间的逻辑关系分别如图1和图2所示。
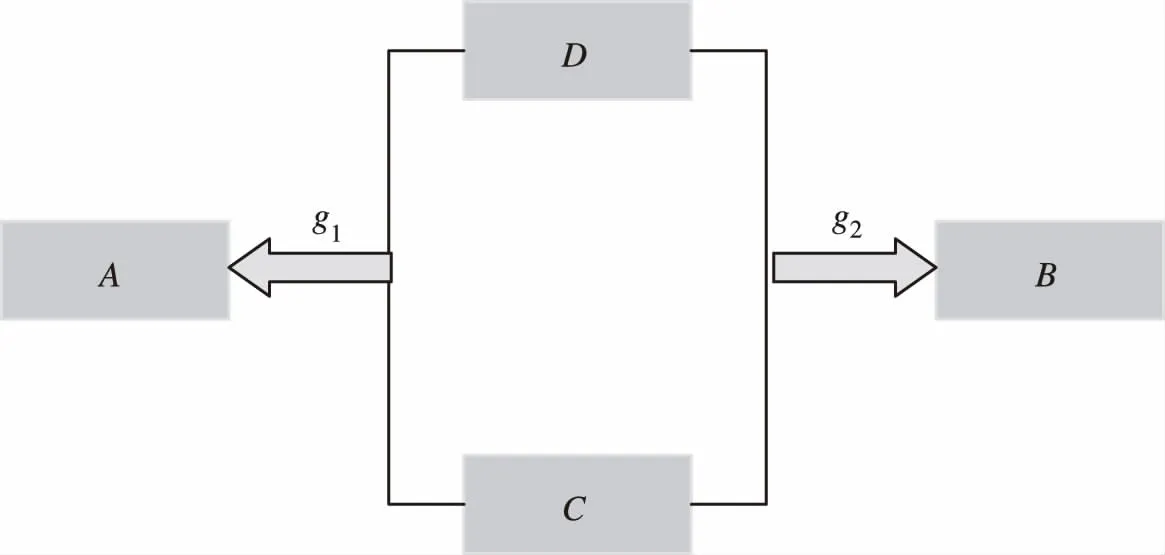
图1 无氧环境中关键基因之间的逻辑关系
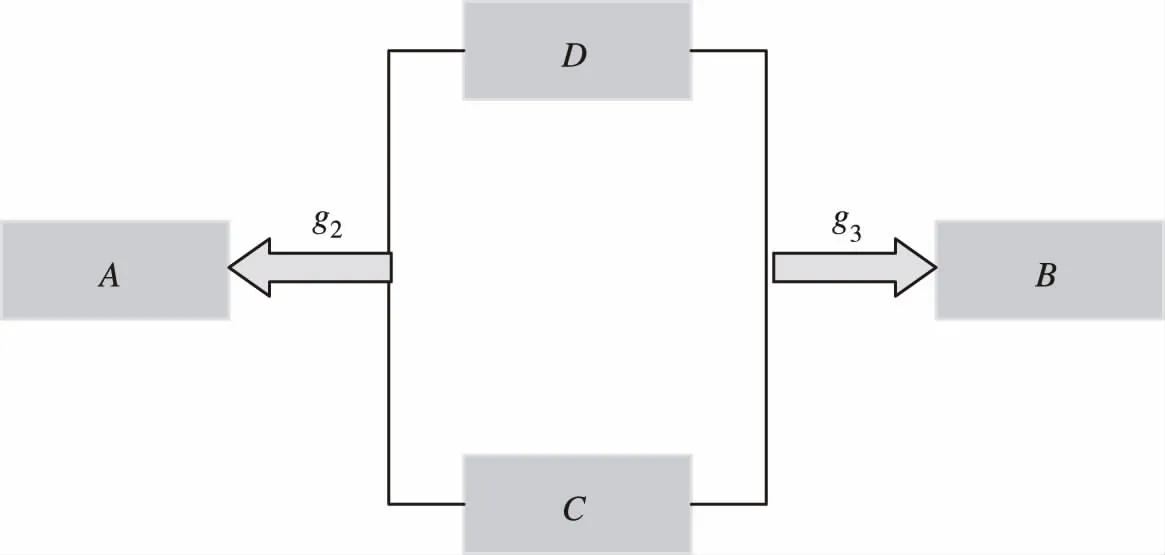
图2 有氧环境中关键基因之间的逻辑关系
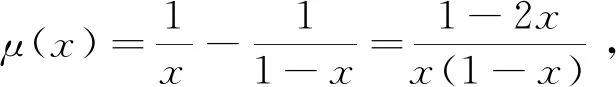
(1)
同样形式的有氧环境下基因表达量方程组为
(2)
式中,ai、bi(i=1,2,3,4)用以表征来自于外界的因素对基因描述所产生的干扰。对于从无氧到有氧的环境切换,方程组的解会发生结构上的变化。假设这是一个参数λ从0到1平稳过渡的过程,那么带参数微分方程组表达式为
(3)
式(3)代表了基因描述的动力学行为,其中包括对平衡点位置及其稳定性的描述,尤其是环境切换过程中整个系统的动力学行为所发生的改变。通过式(1)和式(2)两个方程组的平衡点,能够获得以下两个代数方程组:
(4)
(5)
采用最小二乘法获取式(4)和式(5)两个方程组的参数,得到的结果见表3。

表3 代数方程组参数值估算结果
利用表3中的参数模拟有氧与无氧环境中基因描述的动力学模型数值。首先需要分析方程组的解在接近平衡点时是否逐渐稳定。在无氧环境中,设定关键基因的初始表达量分别为x1(0)=0.02、x2(0)=0.875、x3(0)=0.1、x4(0)=0.83,数值模拟结果如图3所示。
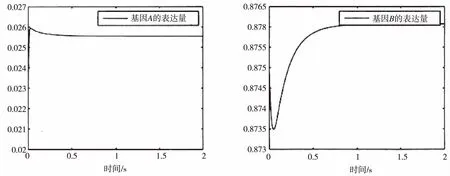
(a)x1(0)=0.02 (b)x2(0)=0.875
由图3可见,在整个过程的初期,各基因的表达量数值均出现一定程度的波动,随着时间的推移,其各自向平衡点位置x1=0.025、x2=0.87、x3=0.224、x4=0.832靠近,说明在无氧环境中平衡点是稳定的。
在有氧环境中,设定关键基因的初始表达量分别为x1(0)=0.835、x2(0)=0.375、x3(0)=0.2、x4(0)=0.2,数值模拟结果如图4所示。
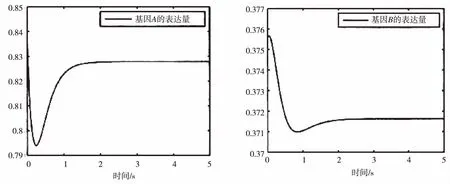
(a)x1(0)=0.835 (b)x2(0)=0.375
由图4可见,在整个过程的初期,各基因的表达量数值均出现一定程度的波动,随着时间的推移,其各自向平衡点位置x1=0.828、x2=0.372、x3=0.319、x4=0.579靠近,说明在有氧环境中平衡点是稳定的。
令λ=0.5,在半有氧环境中,设定关键基因的初始表达量分别为x1(0)=0.02、x2(0)=0.875、x3(0)=0.1、x4(0)=0.83,数值模拟结果如图5所示。
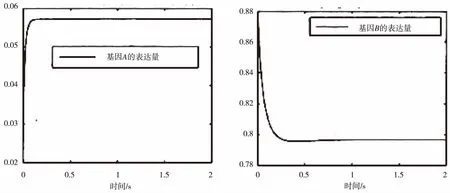
(a)x1(0)=0.02 (b)x2(0)=0.875
由图5可见,在整个过程的初期,各基因的表达量数值均出现一定程度的波动,随着时间的推移,其各自向平衡点位置x1=0.057、x2=0.797、x3=0.265、x4=0.742靠近,说明在半有氧环境中平衡点是稳定的,但平衡点位置相对于有氧和无氧环境有所不同。
在基因C和基因D分别取不同的表达量初始值x3(0)和x4(0)时,对基因A和基因B的表达量轨道性质进行分析,结果如图6所示。
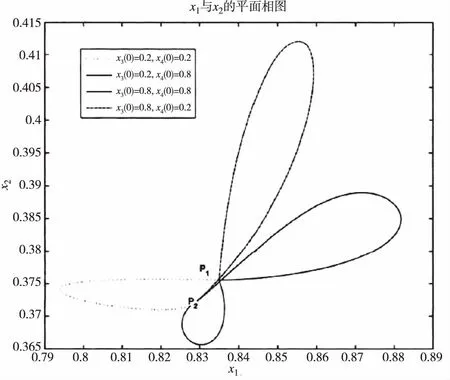
图6 取不同的x3(0)和x4(0)时x1和x2的轨道性质
由图6可见,即使初始值x3(0)和x4(0)不同,x1和x2最终仍向各自的平衡点位置靠近,说明对于初始值,微分方程的解也是稳定的。
3 结 论
通过多个基因间逻辑关系的深入研究能够不断发现新的基因功能和相互作用下产生的机理,利用LAPP方法能够以量化的方式准确精确地描述多个基因间的逻辑关系。本文基于酿酒酵母菌在有氧和无氧环境中4个关键基因的逻辑关系建立了微分方程模型,对方程组平衡点的位置及其稳定性进行了分析,利用已知的实验数据获取方程组参数的估值,在此基础上模拟了基因表达量的数值,证明了多个基因在相互作用的过程中所形成的描述系统是稳定的且具有渐进吸引的性质。实例验证结果表明,本文所提出的方法能够完整地体现多个基因间的逻辑关系,具有很强的实效性。所得到的结论对于多基因描述逻辑关系的研究具有一定的参考价值。
