应用实测资料的桥址区设计风速推算方法改进

张 田，孙铭悦，何 理

（大连海事大学 交通运输工程学院，辽宁 大连 116026）

0 引言

抗风设计是桥梁设计的重要组成部分，桥址区设计风速的推算是桥梁抗风设计的基础，是保障桥梁抗风安全首要解决的问题.目前，推算桥址区风速的一般方法是按实测资料序列计算统计参数，包括均值、标准差σ、离差系数Cv、偏差系数Cs，由以上参数确定一条理论频率分布曲线（极值-I型曲线或Pearson-III型曲线）[1-4]，再计算不同重现期下的设计风速值.然而，由于实测资料观测年限与总体相比相差很远，而且经验频率点分布不是一条光滑连续曲线，直接由统计参数得到的理论频率分布曲线与经验频率点偏离较大.因此，借鉴水文学中推算设计流量的方法[5]，即适线法，通过调整统计参数值，以一定的准则选配出一条与经验频率点拟合最好的理论频率分布曲线，进而推算设计风速.

1 桥址区风速理论频率分布曲线

由于气象记录中的极大风速值是观测期内的极大值，工程中可能遇到的极端风速情况不能简单地取气象资料中观测到的极大值，而需要利用最大风速的频率分布来推算桥位处的风速极值.常用的风速频率分布曲线形式有极值-I型和Pearson-III型[6-9].

1.1 极值-I型分布曲线

极值-I型分布函数为

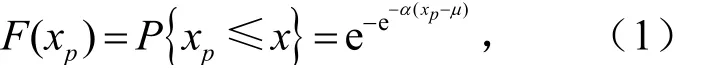
其超过保证率的函数为

式中，x为随机变量；xp为频率p时的随机变量取值；α和μ分别为分布的尺度参数和位置参数，只要利用已知的样本序列x1，x2，…，xn-1，xn，合理估计出参数α和μ的值，则F(x)就可确定.

重现期为T年（累积频率为p=1/T）的风速值可表示为

对于参数α和μ的估计，可以采用矩法.由数学期望和方差的计算公式，进一步推导得

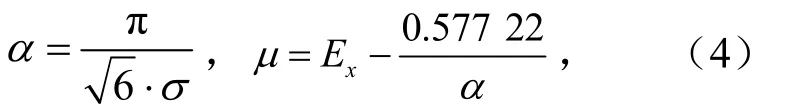
一般采用有限样本容量的均值和标准差作为理论值Ex和σ的近似估计.

1.2 Pearson-III型分布曲线

设风速值为随机变量x，则Pearson-III型曲线的密度函数为

式中，Γ(α)为α的伽马函数，α、β和x0为曲线的参数，可以用样本序列的3个统计参数即均值、离差系数Cv和偏差系数Cs来表示

式中，

式中，n为样本数，σ为样本推算总体的标准差.

计算时不计算α、β和x0，只计算、Cv和Cs，以及给定工程设计的标准，即重现期T的设计要求，则累积频率p=1/T，于是有

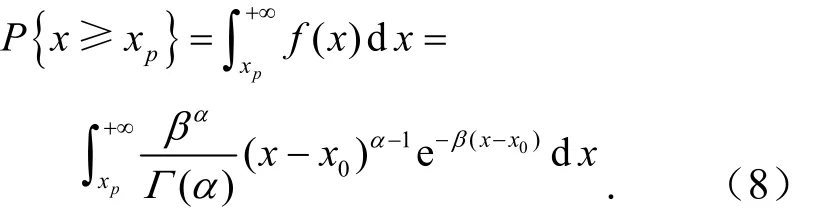
对式（8）进行积分计算，就可以得到频率分布曲线纵坐标值，即累积频率p对应的随机变量值为

式中，Φ为离均系数，是频率和偏差系数的函数，

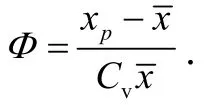
2 风速频率分布曲线的适线调整

2.1 适线法及其准则

适线法为选定最优理论频率曲线的方法，即通过不断优化调整统计参数，绘制多条理论频率曲线，选择其中与实测资料吻合最好的曲线作为最终的理论频率曲线.适线之前需要绘制经验频率点图，其步骤为：将已知的风速序列不论年序按数值大小递减次序排列x1≥x2≥…≥xi≥…≥xn-1≥xn；按Weibull公式，即式（10），计算各风速值的经验频率，并在海森机率格纸上绘出经验频率点群.

式中，P为风速系列中第i项随机变量的经验频率；n为风速系列的容量；i为计算随机变量的序号.

根据概率论与数理统计相关计算方法，适线准则可以采用离（残）差平方和最小准则（OLS准则）和离（残）差绝对值和最小准则（ABS准则）.

①由OLS准则得目标函数为

②由ABS准则得目标函数为

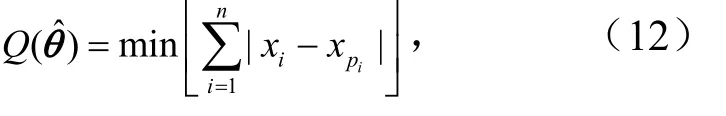
2.2 对极值-I型曲线的适线调整

对极值-I型分布曲线，由上述两种不同的适线准则给出的目标函数，将式（3）代入式（11）、式（12）得

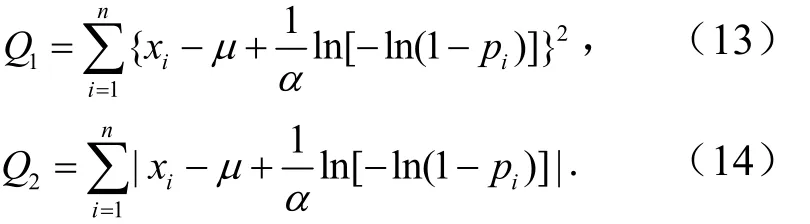
以OLS准则为例给出计算过程，若Q1取最小值，则令和∂Q1∂α=0，则有

式（15）是关于α和μ的非线性方程组，可采用迭代法求解.令

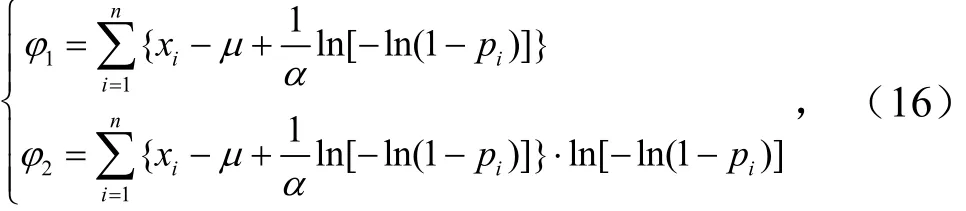
设迭代的初始值为 1α和1μ，将式（4）计算结果作为初始值.将 1φ和 2φ在(1α,1μ)的邻域作Taylor展开，略去高次项后的迭代方程组为

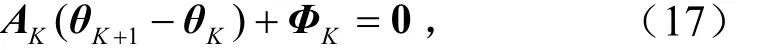
直到满足下式时迭代终止，即

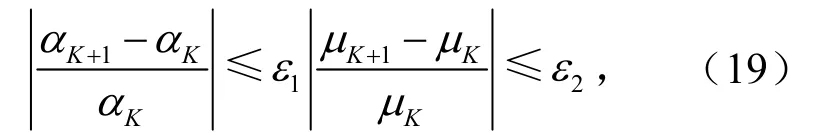
式中，1ε和 2ε为预先给定的允许误差.

2.3 对Pearson-III型曲线的适线调整

对Pearson-III型分布曲线，将式（9）代入式（11）、式（12）得

以OLS准则为例，若Q1取最小值，则令和，有

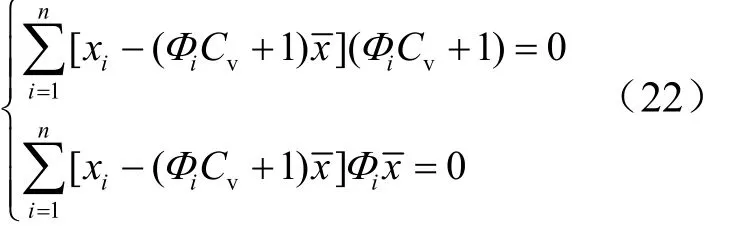
由于经验频率pi为已知，所以给定一个Cs，可以查表求出与pi相对应的Φi，由式（22）按上述迭代求解方法可解出此时使Q1最小的和Cv值.为此，将Cs从0开始，按步长Δ增长（取Δ为0.001），从而得到不同组值，每一组值都对应一条Pearson-III型理论频率曲线，也对应一个按式（20）计算的Q1值，最后选用使Q1最小的一组作为计算结果.

2.4 模拟退火算法计算统计参数

对极值-I型或Pearson-III型分布曲线的参数，虽然可以由上述的迭代方法求解，但从推导过程可以看出，该方法需要推求偏导数矩阵，且涉及到矩阵的求逆过程，求解复杂，收敛速度较慢.可以采用模拟退火算法[10-13]，该方法对优化目标要求较低，一般只需要知道其数值关系，不受函数连续性、光滑性的限制，避免了大量求导数计算.

采用模拟退火算法对于一般无约束优化求最小值问题的求解过程[14-17]如下.

（1）给定起始温度T0、终止温度Tfinal和初始解x0.

（2）在x0的邻域内模拟产生随机扰动Δx.

（3）计算扰动引起的目标函数值的变化ΔE.

（4）若ΔE≤0，接受新值x→x0+Δx，转向步骤（5）；否则，若exp(ΔE/T)＞rand(0,1)，rand(0,1)表示0～1内的随机数，也接受新值x→x0+Δx，转向步骤（5）；否则就拒绝x→x0+Δx，转向步骤（6）.

（5）按退火策略进行降温T→update(T).

采用指数退温方式，设tk、tk-1分别为第k和k-1次迭代时的温度，t0为初始温度，η为参数，tk=η·tk-1.

（6）是否满足T＞Tfinal?若满足，则输出求解结果，结束迭代计算；否则，转向步骤（2）.

3 计算实例

作为实例，以贵州省兴仁县气象站1966-1998年的实测风速资料按不同的推断方法推算气象站10 m高度处的设计风速值，经高度换算后的实测资料[7]列于表1，其中1975年、1992年的资料缺失.

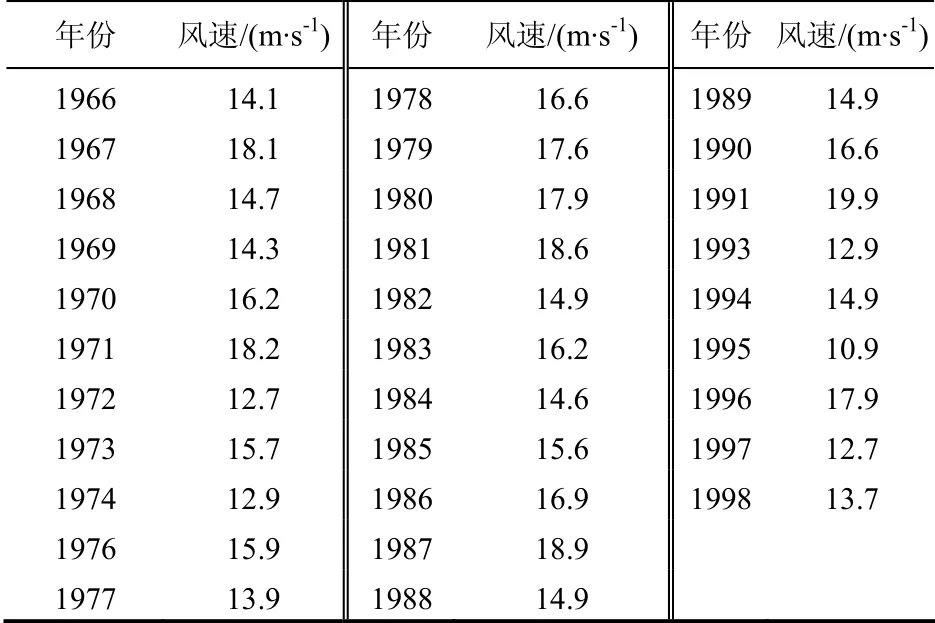
表1 兴仁县10 m高度，年最大10 min平均风速 Tab.1 annual maximum 10 min average wind speed data at 10 m altitude in Xingren County

根据表1的观测资料可以计算经验频率点群图，同时计算各统计参数的初始值，即α0、μ0，、Cv0、Cs0.为了使理论频率曲线与经验频率点群吻合得更好，采用文中提出的模拟退火算法，按2种适线准则逐步调整统计参数以获得最优解，计算的统计参数和目标函数结果列于表2.

表2 不同方法获得的参数及目标函数值 Tab.2 parameters and objective function values obtained by different methods

从表2可以发现，无论采用那种准则，应用模拟退火算法计算出的统计参数均优于直接计算方法.利用上述方法求出的统计参数，来拟合理论频率曲线，见图1，进而求出不同重现期的设计风速列于表3.分布曲线的吻合程度可以通过直接观察分布曲线与经验频率点群图像或判定系数检验、误差平方和检验等方法确定.在图1中将理论频率分布曲线与经验频率点群分布比较，可以直观地看出Pearson-III型曲线作为理论频率分布曲线与经验频率点群吻合得更好.

图1 经验频率点及拟合频率 Fig.1 empirical frequency point and fitting frequency

表3 不同重现期时采用模拟退火算法推算的设计风速 Tab.3 design wind speed calculated by simulated annealing algorithm in different return periods

由表3和图1可以发现，若采用Pearson-III型曲线作为理论频率分布曲线，运用模拟退火算法计算出的统计参数，所得的不同重现期时的设计风速差别不大，可见模拟退火算法计算统计参数是有效可行的.

4 结论

（1）提出适线法，通过不断调整统计参数，使理论频率曲线与经验频率点群尽可能吻合良好，同时给出相应的适线准则及采用模拟退火算法优化统计参数的步骤.

（2）通过实例计算，得到：①基于经验频率点群，采用适线法优化统计参数比由观测数据直接计算统计参数能使理论频率曲线与经验频率点群拟合得更好；②给出适线准则：离（残）差平方和最小准则（OLS准则）和离（残）差绝对值和最小准则（ABS准则），两种目标函数都能很好用于优化统计参数；③采用模拟退火算法，可避免求解统计参数时大量的求导运算，迭代过程简单，对两种适线准则，都能使目标函数快速收敛.