矿井配电网单相接地故障选线方法

谢国民，姜路宁，田锦秀，付 华

（1.辽宁工程技术大学 电气与控制工程学院，辽宁 葫芦岛 125105； 2.山西潞安矿业集团慈林山煤业有限责任公司 李村煤矿，山西 长治 046000）

0 引言

矿井配电网运行中，大多采用小电流接地方式.小电流接地系统的常见故障为单相接地故障，占配电网故障的80%左右[1-2].发生单相接地故障后，由于故障点的电流较小，较短的故障时间不会破坏系统的稳定性，系统可维持运行1～2 h，但长时间处于故障状态会破坏设备绝缘并扩大故障范围[3-5].所以，为避免对矿井配电网运行的损害，单相接地故障发生后，应迅速找出配电网中的线路故障并有效排除，从而保证整个系统的稳定运行.近年来，一些专家学者已经研究出很多不同的故障选线方法，文献[6]提出零序导纳法，根据零序电流的特征分析，比较其零序导纳，该选线方法结构简单，运算量小，但过补偿运行过程中，动作区域与非动作区域会产生交集部分，从而影响继电保护的灵敏度.文献[8]提出小波分析法，该方法适用性较广，但对于较复杂的线路故障，很难选择较为合适的小波基函数.文献[9]提出基于有功功率的注入法，其虽然有效弥补了S注入法的缺陷，但是过渡电阻为0的情况并未考虑在内.

在中性点不接地的小电流接地系统中，系统发生单相接地故障时，故障相线路与非故障相线路在暂态零序电流分量上表现出明显的差异性，同时还受到实际电力系统中的干扰信号和录波装置产生的噪声影响，由此提出基于奇异值分解（Singular Value Decomposition，SVD）与孪生神经网络[10]（Siamese Neural Network，SNN）的故障选线方法.SVD可以有效避免随机干扰信号和高频暂态信号振荡的影响，而SNN则可以比较各线路暂态零序电流的相似性.通过SVD有效地对信号主成分进行提取，并利用SNN比较故障线路、非故障线路两者的暂态零序电流的差异，进而辨识出故障线路.

1 故障暂态特性分析

以中性点经消弧线圈接地为例，单相接地故障就相当于在故障点处增加一个等效的零序电压源u0，u0=Umsin(ωt+φ)，暂态等效电路见图1.

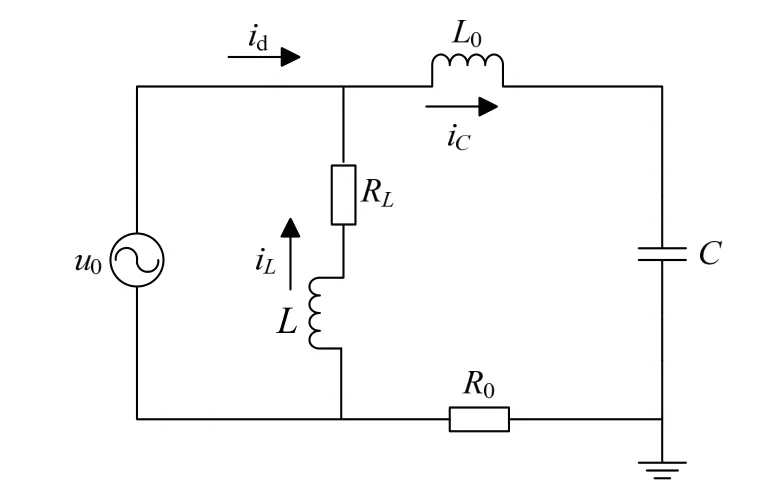
图1 暂态等效电路 Fig. 1 temporarily equivalent circuit

图1中，C为系统中的对地电容；R0和L0分别为故障时系统中的等效电阻和等效电感；RL和L分别为消弧线圈的电阻和电感；ω为电源角频率；φ为电源初相位.

1.1 暂态电容电流分析

对图1进行分析，可得到

对式（1）进行拉普拉斯变换，得到其暂态电容电流为

式中，ICm为电容电流幅值；ωf为暂态自由振荡分量的角频率；δ为衰减系数.

1.2 暂态电感电流分析

分析图1中的电感所在回路，列出方程为

式中，φL为磁通量，Wb；Nz为线圈匝数.

可以得到暂态电感电流为

式中，ILm为电感电流幅值，A；τL为时间常数，s。

将暂态电容电流和电感电流相加，即为所求接地故障点的电流id，经过整理，可以得到

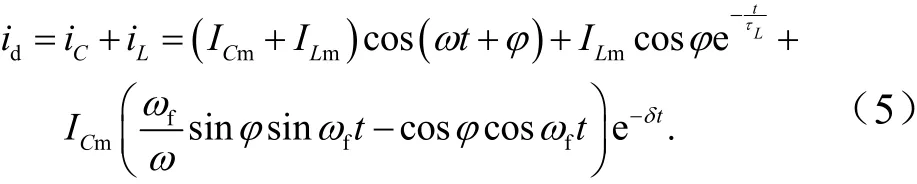
式（5）中多项式含有3项，其中第一项表示故障电流的稳态分量，后两项为其暂态分量.暂态分量包括暂态电容电流的自由振荡分量和暂态电感电流的直流分量.

由式（5）可知，暂态分量中的电容电流显著区别于电感电流，主要表现为频率和幅值的明显不同，所以在暂态过程中不能相互补偿，甚至还会相互叠加，并且iL只流过故障电路，iC流过故障电路和非故障电路.

通过上述分析可知，小电流接地系统在发生单相接地故障时，故障相线路与非故障相线路产生了在波形上具有很大差异的暂态零序电流.

2 故障信号的特征提取

2.1 故障信号的分解

设x(n)（n=1，2，…，N）是长度为N的一维时间序列，采用延迟法对x(n)进行重采样，采样间隔设为τ（通常τ=1），则重构吸引子轨迹矩阵[12]为

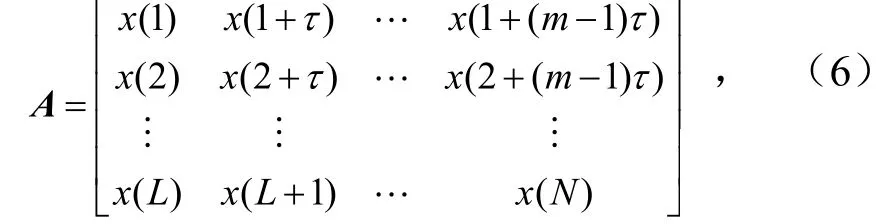
式中，A为L×m维矩阵，秩为r(r≤min(L,m))；N=L+(m-1).

对矩阵A进行奇异值分解

式中，U和V分别为L×L和m×m的正交矩阵，代表左右奇异阵，Λ为L×m的非负对角阵.

设L≤m，则σ1≥σ2≥…≥σr＞0，σr+1=σr+2=…=σL=0，称为矩阵A的奇异值.

2.2 故障信号特征提取

特征提取对于故障选线具有关键性的作用，采用SVD算法对各线路故障信号的主成分进行分离，以提取故障线路特征.

为表示一维时间序列构造吸引子轨迹矩阵的过程，引入一个抽象函数F(x)，则式（7）可写为

反函数为

表示吸引子轨迹矩阵元素重构原始时间序列过程.

由式（7）可知，矩阵A的特征信息体现在矢量U和V构成的矢量子空间中.由此可以得到，信号x(n)的主要成分对应矩阵A最大特征值σmax对应的子空间.所以信号x(n)的主要成分为

式中，ul、vl分别为最大特征值σmax对应的左右奇异向量.

3 建立故障选线模型

3.1 SNN故障选线模型

设计SNN故障选线模型的网络结构[13]见图2.图2中有X1和X2两个输入分支，隐藏层由2个共享权值和偏置等参数的子网络组成.

图2 SNN网络结构 Fig. 2 SNN network structure

将SVD提取后的主成分部分作为SNN的输入，假设神经网络共有l层，则第l层有p(l)个神经元，X1=(x1,x2,… ,xd)，则顶层输出为

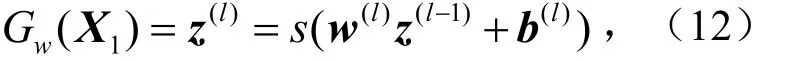
式中，s为非线性激活函数，w(l)为p(l)×d的共享参数矩阵，b(l)是长度为p(l)的偏置向量.

3.2 故障选线模型参数优化

对所得到的矢量Gw(Xi)进行相似性测度，可进一步得出相似度的情况.使用度量函数表示样本特征彼此之间的欧氏距离，选用二范数作为度量函数，则

为使选线模型达到更精确更迅速的效果，应使损失函数最小，即损失函数的值越小，代表预测值与真实值之间的差距越小.利用反向传播算法来调节权值w，在模型算法推演时，如果两个输入属于同一类别，则使Dw减小；如果两个输入属于不同类别，则使Dw增大.

损失函数为

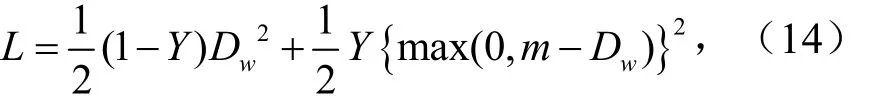
式中，m为阈值；Y为样本特征标签.当X1和X2为不同类别时，Y=1；当X1和X2为同一类别时，Y= 0.

采用随机梯度下降算法[14]（SGD）优化参数w、b，参数w、b按其负梯度方向来更新.

当两输入数据为同一类别时，则

此时，得到

式（16）、式（17）中，α为学习率.

当两输入数据为不同类别时，则

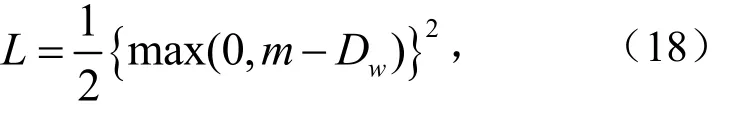
且Dw＜m时

3.3 故障选线方法的流程

基于SVD-SNN的矿井配电网单相接地故障选线方法的流程见图3.

图3 故障选线方法的流程 Fig.3 fault line selection method flow

4 算例

4.1 算例分析

为验证SVD算法具有良好的主成分提取特性，假设有一模拟信号

式中，f1取10 Hz，f2取50 Hz，noise为噪声干扰.

图4为 (tx)时域波形.

图4 模拟信号时域波形 Fig. 4 waveform of area at time of simulation signal

对该模拟信号进行SVD主成分提取，并对提取前后的信号分别进行FFT变换，频谱见图5、图6.可以看出，SVD分解能有效剔除原始信号中的次要成分和噪声信号干扰，突出了原始信号的主要特征.

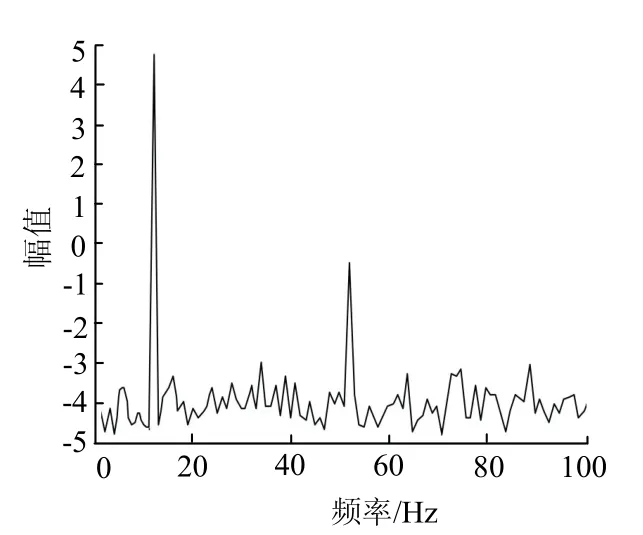
图5 原始信号的频谱 Fig. 5 spectrum of original signal

图6 SVD分解后的频谱 Fig.6 spectrum after SVD decomposition

4.2 仿真模型搭建

利用Matlab搭建了10 kV小电流接地系统模型，分析故障相暂态分量，系统简化示意见图7.其中，T为变压器，变比为110 kV/10 kV，L为消弧线圈，R为消弧线圈的电阻.消弧线圈为10%过补偿，发生故障时，采用全补偿方式.

图7 系统简化示意 Fig.7 schematic of system simplification

4.3 仿真结果

设线路L1故障，故障距离设为3 km，故障初始角设为60°，接地电阻为20 Ω.应用SVD算法提取各线路信号的主成分，时窗取8 ms，各线路暂态零序电流波形，见图8.

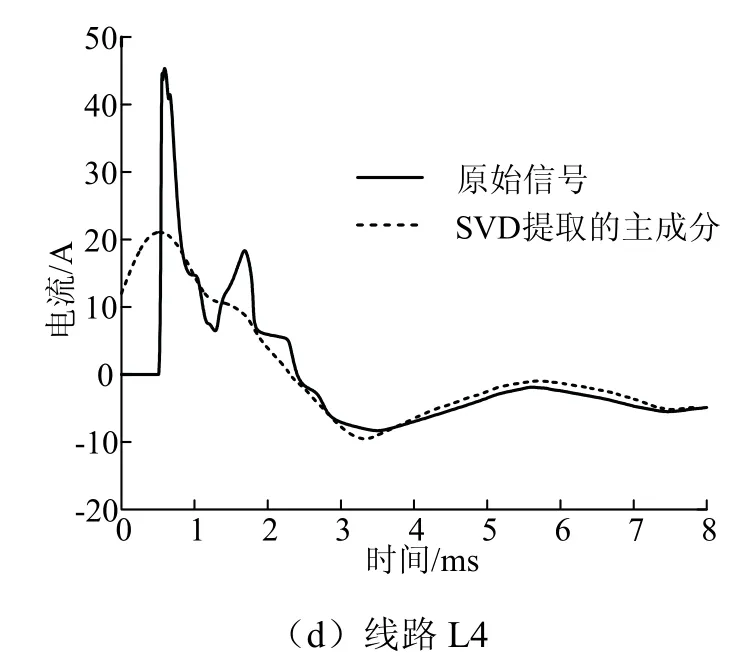
图8 各线路暂态零序电流波形及其SVD主成分 Fig.8 temporary zero-order current waveform of each line and its SVD main component

由图8可见，故障线路与非故障线路在波形上具有很大差异性，且SVD提取的主成分可以很好地突出原始信号的变化趋势并具有平滑特质.

选用具有一层隐含层的前馈神经网络来构建SNN模型的子网络，选取sigmoid函数作为神经元的激活函数.通过改变线路参数（故障线路、故障距离、故障初始角、接地电阻）获得每条线路100组样本数据，其中每条线路的前40组数据作为训练集，其余数据作为测试集.

图9为经过SNN测试后得到的故障选线结果.图9纵坐标1、2、3、4分别代表线路L1故障、线路L2故障、线路L3故障和线路L4故障.

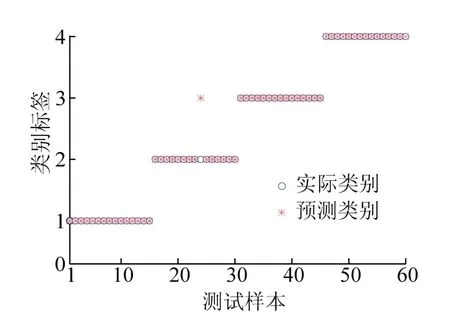
图9 测试结果 Fig. 9 test result chart

4.4 对比分析

传统的相似性度量方法还有欧氏距离（ED）和动态时间弯曲距离（DTW），现将SVD-SNN与SVD-ED、SVD-DTW的选线准确性进行对比分析，得到结果见表1.

表1 选线准确性对比分析 Tab.1 comparison analysis of line accuracy

由表1可以看出，SVD-SNN选线方法相较于传统的欧氏距离选线方法（SVD-ED），以及动态时间弯曲距离选线方法（SVD-DTW），具有更高的精准度.

5 结论

（1）在矿井配电网中，针对发生单相接地故障的情况，从暂态零序电流波形的特点出发，提出了基于SVD-SNN的故障选线方法.

（2）SVD-SNN方法可以有效提取各线路暂态零序电流信号的主成分，避免了噪声等信号的干扰；该方法应用于矿井配电网单相接地故障的情况，具有良好的适用性；与SVD-ED方法和SVD-DTW方法相比，该方法具有准确性更高、精确性更强的特点.