CFRP约束钢管高强混凝土轴压短柱承载力的极限分析
2022-03-28焦楚杰何松松李宏宇
李 松,焦楚杰,何松松,梁 健,李宏宇
(广州大学 土木工程学院,广东 广州 510006)
随着高强水泥、高效减水剂的产生及混凝土拌合工艺的改善,高强混凝土(high strength concrete,HSC)的制备强度等级日趋渐高。HSC因具有强度高、变形小、耐久性和质密性均高于普通混凝土等优点,HSC的构件截面尺寸可以有效地缩小,避免产生胖柱。然而,HSC延性较差,呈高度脆性,也制约其工程应用。将HSC灌注入钢管形成钢管HSC复合构件,既可以让HSC抑制钢管的向内屈曲,也可以让钢管从外部限制核心HSC的膨胀。在利用HSC高强特性的同时还能改善HSC的脆性,特别是钢管的约束不仅可以提供压缩方向的延性,对于抗拉延性也能有效的给予补充,因此,HSC复合钢管形成的钢管高强混凝土(钢管HSC)构件受到了国内外学者推崇[5-8]。
钢管HSC因其高强特性可以减小构件截面的面积,可为大跨度、高层等建筑提供性能优越的竖向构件。但对于轴压作用下的钢管HSC短柱,当钢管屈服后,HSC的横向变形系数急剧增大,不利于构件进一步承受更高荷载。采用优质的复合材料来约束钢管HSC,可以有效的解决上述缺陷,碳纤维增强复合材料(carbon fibre reinforced polymer,CFRP)是一类质轻高强、抗腐蚀佳、耐久性好并易于施工的高性能材料,被广泛运用于混凝土结构与钢结构的加固。CFRP约束钢管高强混凝土(CFRP约束钢管HSC)构件因承载力提高较大,其加固作用被广泛认可接受。因核心混凝土为高强脆性较大的HSC组合构件,其三向受压状态之下的力学性能与普通混凝土有较大的区别,与CFRP约束钢管HSC轴压短柱的受力破坏过程也有较大的差异,这类差异也体现在CFRP、钢管与HSC3类材料的应力分析中,因此,有必要推导该类组合构件承载力理论公式。
近年来,对于FRP约束钢管混凝土轴压短柱极限承载力方面的研究较多,主要研究了CFRP层数、钢管壁厚、混凝土强度、FRP种类等影响因素对承载力的影响。上述文献在考虑约束混凝土受钢管围压与CFRP围压作用时,其侧压效应系数取值为同一数值,实际中钢管的约束机制与CFRP的约束机制存在显著差异。同时,已有研究表明,HSC横向变形系数略小于普通混凝土,侧压力对于HSC抗压强度的提高较小,因此,现有理论公式不能直接应用于CFRP约束钢管HSC短柱。本文依据文献[22],对轴压下的CFRP钢管HSC短柱进行工作机制分析,并探讨CFRP钢管HSC和CFRP钢管混凝土受力过程的异同。基于极限平衡法,通过分析3类材料的应力状态,推导得出极限承载力的理论计算公式,且与文献[22]的试验实测值以及所提出的极限承载力计算公式相比较,验证理论计算公式的适用性与准确性。最后,探讨所得理论模型计算值随CFRP层数和钢管壁厚变化规律,并对变化的差异进行分析。
1 CFRP约束钢管高强混凝土和CFRP约束钢管混凝土轴压短柱工作机制
1.1 CFRP约束钢管高强混凝土短柱的工作机制
图1为典型的CFRP约束钢管高强混凝土短柱的应力-应变曲线,结合文献[15-16, 22-24]中的试件受力破坏过程可知,CFRP约束高强HSC试件破坏过程与CFRP约束钢管混凝土相似,不同之处主要体现在核心HSC的高强与脆性特性,从而造成了工作机制的差异。因此,从HSC、钢管与CFRP3类材料在组合构件中的受力特点进行工作机制分析如下:
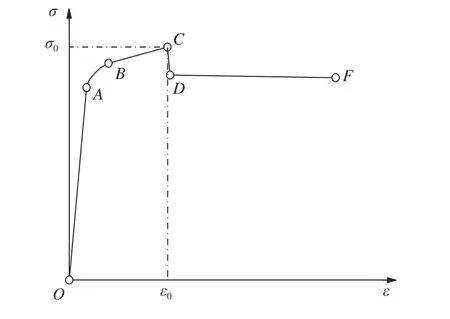
图1 典型CFRP约束钢管HSC短柱应力-应变曲线Fig. 1 Typical stress-strain curve of CFRP confined steel tube-HSC stub column
第1阶段为弹性阶段(OA
段)。初始荷载阶段中,HSC横向变形系数比钢管的小,两者不发生相互挤压,钢管与HSC分别单独承受轴向荷载,此阶段CFRP基本上不受环向拉应力。第2阶段为弹塑性阶段(AB
段)。随着加载,钢管进入了弹塑性状态,而HSC仍处于弹性阶段,因此导致钢管与HSC之间出现了径向压力,钢管管壁上出现环向拉应力,进而发展到CFRP上出现环向拉应力,该阶段已有较小程度的内力重分布,结束的标志为钢管屈服。第3阶段为硬化阶段(BC
段)。钢管的屈服促使试件的应变急剧发展,HSC开始出现微裂缝,这更加剧了HSC和钢管的相互作用,从而导致了纵向应力较大程度的重分布,钢管所受纵向应力较大转变为环向应力,而使得CFRP产生较大的约束作用,而不断的提供侧压力,核心HSC达到更高的抗压强度。该阶段中钢管纵向应力向环向应力的转化减小促使HSC抗压强度的提高,当HSC纵向抗压强度达到最大值时,试件中部区域的部分CFRP断裂,试件达到极限强度σ。第4阶段为强化阶段(CDF
段)。CFRP部分断裂后,极限强度从C
点陡然下降到D
点,导致核心HSC的侧压力大幅度减小,但核心HSC处于钢管残余环向应力约束之下,仍受到部分未完全破坏的CFRP环向应力约束,故应力-应变曲线又从D
点发展至F
点,由此可见,试件残余强度随CFRP层数与钢管壁厚增大而回升幅度增大。1.2 CFRP约束钢管高强混凝土与CFRP约束钢管混凝土短柱轴压破坏过程的异同
图2为典型的CFRP约束钢管HSC破坏模式。实质上,CFRP约束钢管HSC短柱可以看作是CFRP约束钢管混凝土中的普通混凝土被高强的HSC替代所形成的组合构件。与CFRP约束钢管混凝土相比,CFRP约束钢管HSC短柱的受力破坏不同之处,主要是基于核心HSC的特性所致:

图2 典型的CFRP约束钢管高强混凝土短柱破坏模式[22]Fig. 2 Typical failure mode of CFRP confined steel tube-HSC stub column[22]
1) 与CFRP约束钢管混凝土相比,CFRP约束钢管HSC轴压短柱受力过程中弹性阶段较长,弹塑性阶段较短,CFRP约束钢管高强混凝土短柱到达极限承载力之前,其外表面几乎没有变化。究其本质原因,在于高强的HSC应力-应变曲线弹性阶段较长,而弹塑性阶段较短,其破坏是急剧性的。
2) 因HSC应力-应变曲线上升段基本呈直线发展,故CFRP约束钢管HSC柱弹塑性阶段中HSC仍处于线弹性阶段,其进行弹塑性阶段的原因在于钢管进入了弹塑性阶段,钢管主动挤压HSC导致了两者的相互作用。CFRP约束钢管混凝土中弹塑性阶段的引起在于普通混凝土的微裂缝发展导致其横向变形系数大于钢管的横向变形系数,普通混凝土的变形主动导致了与钢管发生了挤压作用。由此可知,弹塑性阶段中,钢管和HSC的相互作用与挤压程度弱于钢管和普通混凝土的相互作用。
3) HSC高强特点使得HSC的裂缝发展较普通混凝土晚,因此,其侧压应力发展速度不如普通混凝土。但一旦达到HSC裂缝发展临界强度点时,其裂缝的发展又是急剧的,这也印证了HSC脆性较大的特性。同时表明,CFRP约束钢管HSC短柱中,钢管与HSC的相互挤压作用时间是不充分的,故HSC的侧向膨胀的完全性不如CFRP约束钢管混凝土柱中的普通混凝土,其侧压效应系数也比CFRP约束钢管混凝土的要小。
4) 轴压作用下CFRP约束钢管HSC短柱的破坏模式多数呈压缩剪切破坏,而CFRP约束钢管混凝土短柱则多数呈鼓曲破坏。其原因在于,HSC与普通混凝土相比脆性破坏是急剧性的,与钢管之间的内力重分布是迅速发展的,且HSC裂缝发展面的反复挤压作用时间较短,CFRP与钢管提供较大约束时,剪切破坏的趋势已然形成,只有当CFRP层数较多和钢管壁厚较大时才会出现鼓曲破坏。
2 CFRP约束钢管高强混凝土短柱极限承载力计算
CFRP约束钢管HSC短柱的极限承载力可忽略变形的影响,采用极限平衡法进行推导。根据文献[26-28],对于CFRP约束钢管HSC轴压短柱中3类材料分别进行应力分析,绘制CFRP约束钢管HSC示意图与材料横截面和竖向面微元体应力图如图3所示。图3中,D
、d
、t
和L
分别为钢管的外直径、内直径、壁厚和长度,R
和r
分别为钢管的外半径、内半径,t
为CFRP的约束厚度。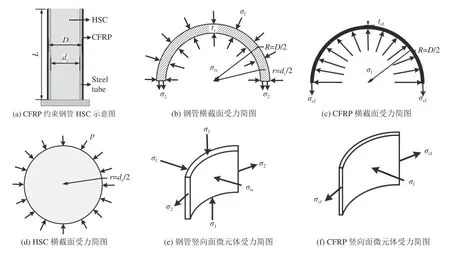
图3 CFRP约束钢管HSC短柱受力图Fig. 3 Schematic of CFRP confined steel tube-HSC stub column
为方便分析,引入钢管套箍系数ξ和CFRP套箍系数ξ两个约束指标,定义如下:
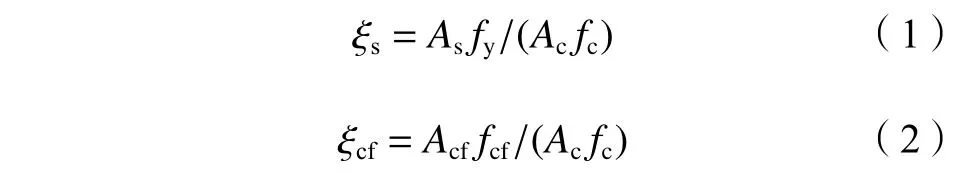
A
、A
、A
分别为短柱中核心混凝土横截面面积、钢管横截面面积、CFRP横截面面积,f
、f
、f
分别为无约束混凝土轴心抗压强度、钢管屈服强度、CFRP抗拉强度。2.1 HSC应力分析
HSC受到CFRP和钢管的约束作用,处于轴向压缩和侧向均匀围压的3向应力状态,因此约束作用下的HSC轴向抗压强度σ比单轴抗压强度f
要大得多,σ与侧压力p
之间具有线性关系: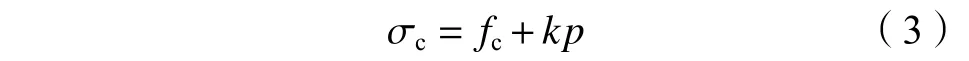
k
为侧压效应系数。定义CFRP对HSC提供的侧向压力为σ,钢管对HSC提供的侧向压力为σ,因此式(3)可以写成:
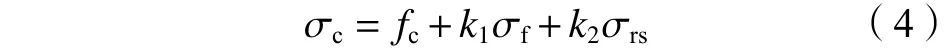
k
为CFRP提供侧压力下的侧压效应系数,k
为钢管提供侧压力下的侧压效应系数。2.2 钢管应力分析
图3(b)与(e)中,设钢管内径为d
,因D
/t
≥ 20,可近似认定钢管的径向应力为0。并将钢管当作理想塑性材料,根据Von Mises屈服条件得: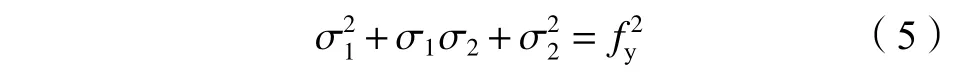
式中,σ为钢管轴向应力,σ为环向应力。
2.3 CFRP应力分析
CFRP为单向纤维,因其在厚度上连续均匀且壁薄的特点,可忽略厚度和轴向方向的应力。根据CFRP约束钢管高强混凝土受力破坏过程中的硬化阶段分析可知,CFRP几乎仅受环向拉应力且CFRP断裂前为线弹性发展,由胡克定律得:
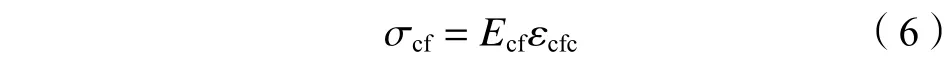
E
为CFRP沿纤维方向上的弹性模量。2.4 CFRP约束钢管高强混凝土短柱极限承载力分析
上述对于CFRP和钢管的应力分析中,CFRP厚度t
与钢管壁厚t
都较薄,假设图3(e)与(f)中的σ与σ沿钢管和CFRP均匀分布,可由图3(b)与(c)分析得: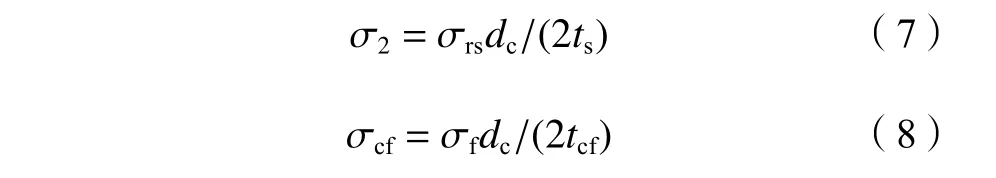
A
= πd
/4。由于t
与t
都较薄,可近似取A
= πd
t
与A
= πd
t
,故求得: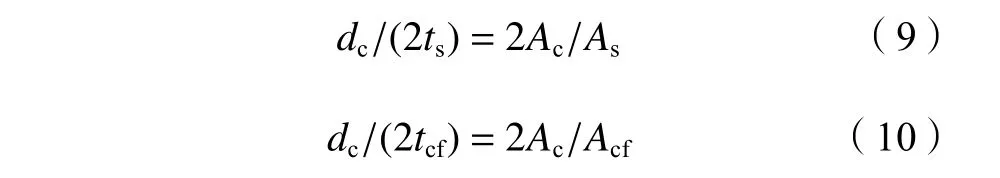
将式(9)与(10)分别代入式(7)与(8)可得:
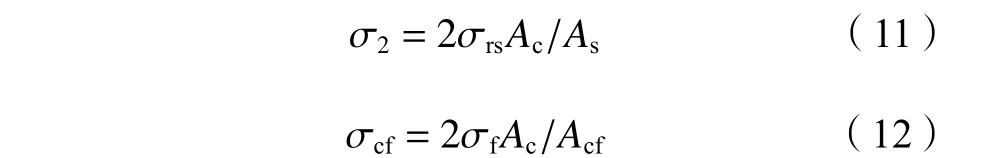
式(4)中,CFRP提供的侧向压力可写成:
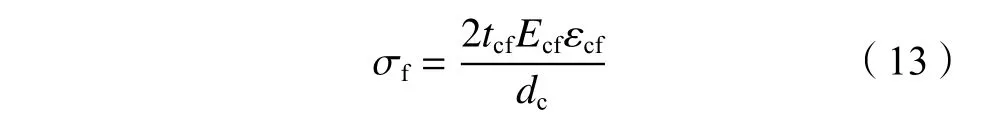
根据式(2)与(13)可得:
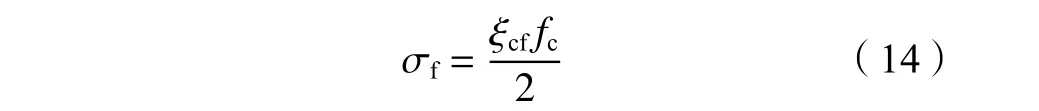
钢管屈服时由式(5)解得:
CFRP约束钢管HSC短柱的极限承载力计算值N
由钢管与HSC共同提供,即有: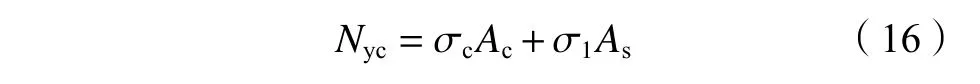
将式(4)、(11)、(14)和(15)代入式(16),整理得:

k
与k
的取值,一般是根据大量试验总结来确定,由于试验条件的差异,侧压效应系数取值存在差异。由CFRP约束钢管HSC和CFRP约束钢管混凝土短柱轴压破坏过程的异同分析可知,约束HSC的侧压效应系数比约束普通混凝土的要小。本次分析中采用文献[31]收集的107根钢管高强混凝土计算的侧压效应系数取值k
=2.11。而对于CFRP约束HSC的k
取值,因核心HSC强度较高,侧压效应系数和强度有着内在的联系,可采用文献[32]提出的公式计算: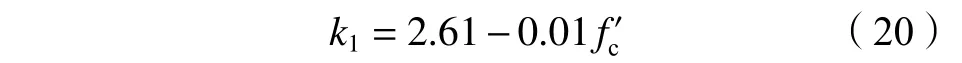
f
为混凝土圆柱体抗压强度,f
与立方体抗压强度f
,其转换公式为: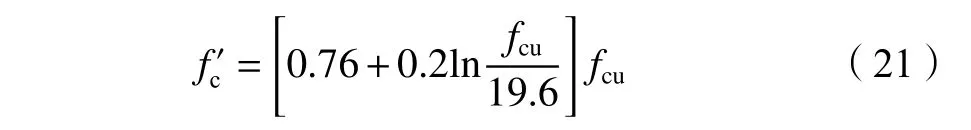
3 试验验证
3.1 试验概况
为验证所提承载力模型的正确性,对文献[22]中12根CFRP约束钢管RPC短柱与4根钢管RPC短柱轴压试验进行分析。该研究中核心RPC为约束高强混凝土,所用钢管采用无缝钢管,外径D
为100 mm,高度L
为300 mm,RPC设计强度为120 MPa,CFRP采用单向纤维环向粘贴。试验以钢管厚度t
(2~5 mm)和CFRP层数n
(0~3层)为变量。试验实测RPC立方体抗压强度f
为127.7 MPa,棱柱体抗压强度f
为108.1 MPa,钢管与CFRP材质性能如表1和表2所示。表1 钢管材质性能
Tab. 1 Material properties of steel tube
ts/mm 屈服强度fy/MPa极限强度σy/MPa弹性模量Es/GPa泊松比µs 356 467 208 0.295 3 310 421 204 0.295 4 291 408 202 0.295 5 318 416 207 0.295 2
表2 CFRP材质性能
Tab. 2 Material properties of CFRP
单层厚度tcfc/mm CFRP 3 400 1.63 238 0.167材料 抗拉强度fcf/MPa极限应变εcf/%弹性模量Ecf/GPa
3.2 两类计算模型的分析比较
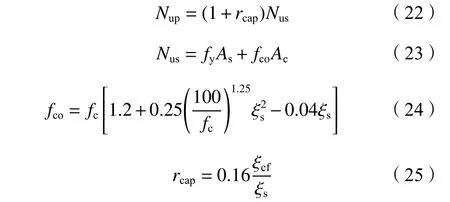
N
为钢管高强混凝土的极限承载力计算值,r
为钢管高强混凝土在CFRP的约束下的提高系数。对于承载力模型(式(19)~(21)),将文献[22]中的f
代入式(21)中,解得f
= 117.8 MPa,将该值代入式(20),解得k
=1.432。将k
与k
代入式(19)解得: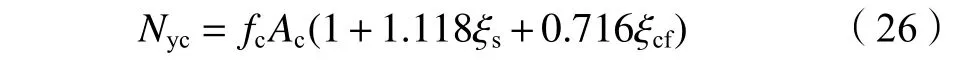
对比分析文献[22]所建模型与本文理论模型可知:
1) 本文理论模型形式上比较简单,而文献[22]中所建模型相对较为繁琐。
2) 本文理论模型所计算的侧压效应系数随核心混凝土强度等级而变化,这吻合了随着核心混凝土强度等级的提高,约束混凝土中约束作用是下降的这一规律;文献[22]中所建模型是在已有钢管HSC的模型上,通过钢管HSC在CFRP的约束作用下的提高程度进行计算,关键是提高系数r
的计算。3) 对本文理论模型式(26)中的套箍系数ξ与ξ,分别求偏导可得∂N
/∂ξ= 1.118,∂N
/∂ξ= 0.716,分析偏导结果可知,钢管的约束对核心混凝土承载力的贡献力度大于CFRP的约束贡献值,而文献[22]中所提模型,可通过提高系数r
,了解CFRP的约束对钢管HSC的贡献力度。3.3 试验结果和模型预测结果比较
将文献[22]中极限承载力试验实测值和本文理论模型计算结果进行比较,并结合文献[22]中所建模型计算结果进行分析,对比结果如表3所示。表3中,N
为试验实测极限承载力,N
为文献[22]中所建模型的极限承载力,N
为本文理论模型计算的极限承载力。通过表3计算可知:N
∶N
的平均值为1.05,标准差为0.066,变异系数为0.063;N
∶N
的平均值为0.978,标准差为0.035,变异系数为0.036。由此可知,本文推导的理论公式偏于安全,相比于N
∶N
,其标准差更小,计算离散性与波动性也更小。将N
和N
的值与试验实测值N
进行比较,结果如图4所示。从图4可以看出,本文理论推导公式计算偏差在10%以内,文献[22]中所建模型偏差略大。综上所述,本文推导的理论模型计算吻合较好,验证了推导的正确性。表3 CFRP约束钢管HSC短柱极限承载力试验值与预测结果对比
Tab. 3 Comparisons of ultimate bearing carrying between experimental and prediction results of CFRP confined steel tube-HSC stub columns
注:试件编号规则以C120t3CF2为例,C120为核心混凝土强度等级为120 MPa,t3表示钢管壁厚为3 mm,CF表示粘贴的FRP材料为碳纤维布(CFRP),2表示CFRP粘贴层数为2层;、和分别为文献[22]中试验实测承载力、文献[22]中所建模型的承载力计算值和本文理论模型承载力计算值。
试件编号 D×ts×L/(mm×mm×mm) ξs ξcf Nu/kN Nyc/kN Nup/kN Nyc·Nu-1 Nup·Nu-1 C120t2CF0 103×2×303 0.272 0 1 081 1 084 1 228 1.00 1.14 C120t2CF1 103×2×303 0.272 0.221 1 238 1 215 1 387 0.98 1.12 C120t2CF2 103×2×303 0.272 0.442 1 306 1 347 1 547 1.03 1.18 C120t2CF3 103×2×303 0.272 0.663 1 428 1 478 1 707 1.04 1.20 C120t3CF0 102×3×303 0.370 0 1 132 1 105 1 179 0.98 1.04 C120t3CF1 102×3×303 0.370 0.233 1 288 1 235 1 298 0.96 1.01 C120t3CF2 102×3×303 0.370 0.466 1 379 1 365 1 417 0.99 1.03 C120t3CF3 102×3×303 0.370 0.699 1 485 1 496 1 536 1.01 1.03 C120t4CF0 101×4×304 0.484 0 1 221 1 130 1 259 0.93 1.03 C120t4CF1 101×4×304 0.484 0.246 1 340 1 259 1 362 0.94 1.02 C120t4CF2 101×4×304 0.484 0.492 1 474 1 388 1 464 0.94 0.99 C120t4CF3 101×4×304 0.484 0.738 1 621 1 517 1 567 0.94 0.97 C120t5CF0 102×5×306 0.675 0 1 370 1 259 1 400 0.92 1.02 C120t5CF1 102×5×306 0.675 0.253 1 400 1 389 1 484 0.99 1.06 C120t5CF2 102×5×306 0.675 0.506 1 508 1 519 1 568 1.01 1.04 C120t5CF3 102×5×306 0.675 0.759 1 659 1 649 1 652 0.99 1.00
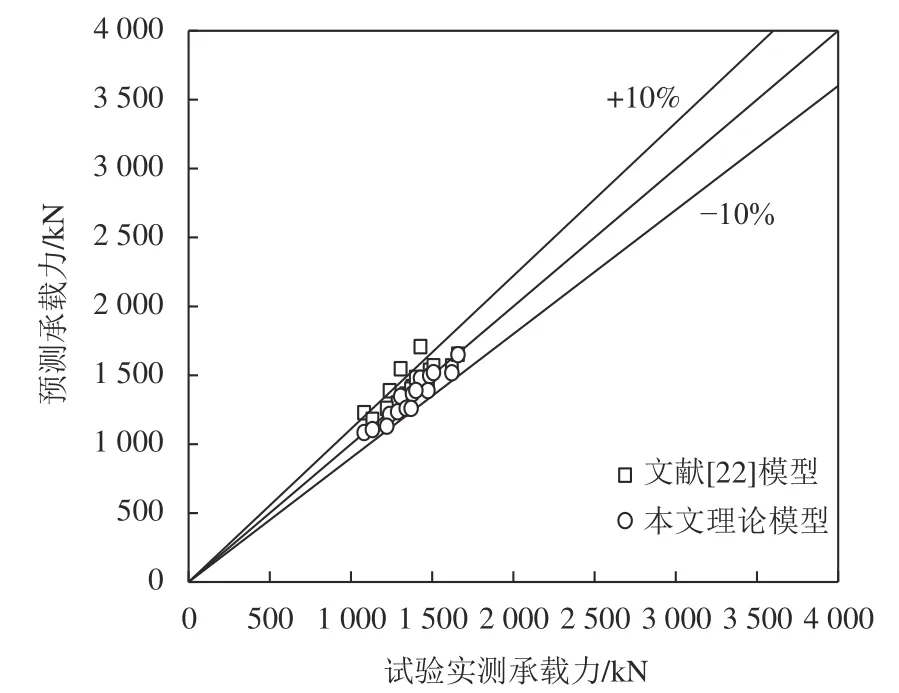
图4 预测极限承载力与实测极限承载力对比Fig. 4 Comparison of experimental and predicted results
图5和6分别为本文理论模型极限承载力计算值N
随CFRP层数n
和钢管壁厚t
的变化。由图5、6分析可知:CFRP层数对于极限承载力的提高幅度较为明显;钢管壁厚对于极限承载力的提高幅度在t
= 2~4 mm时趋于平缓,而在t
= 5 mm时有较大的提高,这表明对于高强的HSC,钢管壁厚较大时约束效果比较明显。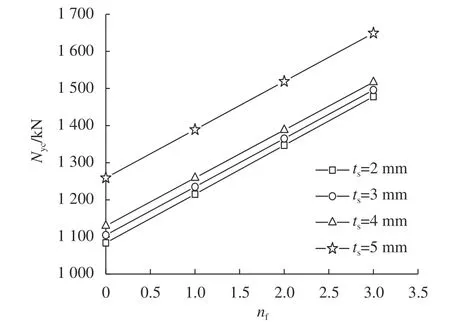
图5 极限承载力Nyc随CFRP层数nf变化Fig. 5 Ultimate bearing capacity varies with nf
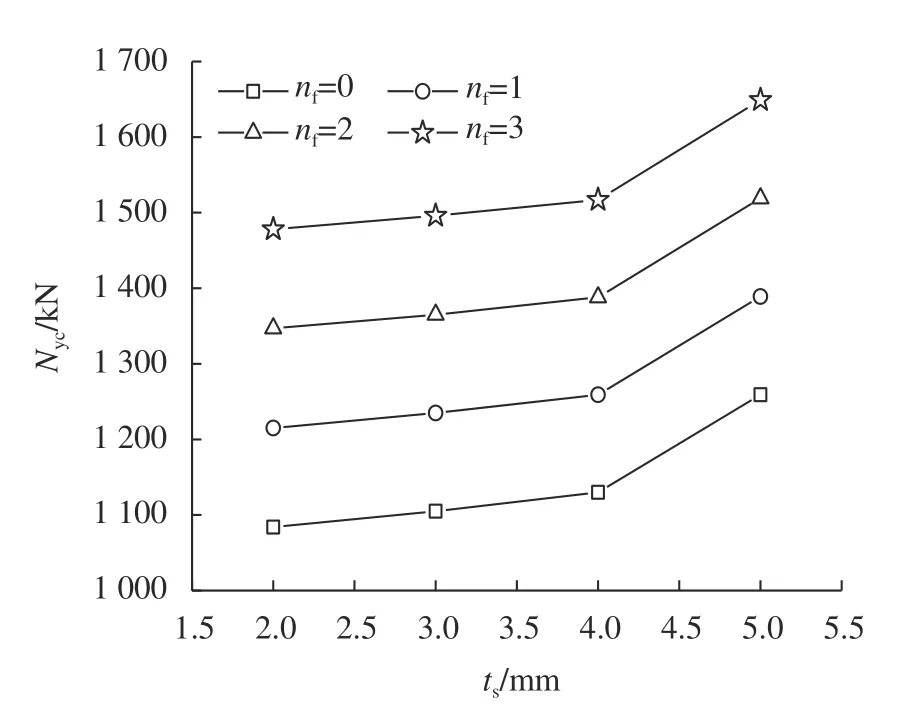
图6 极限承载力Nyc随钢管壁厚ts变化Fig. 6 Ultimate bearing capacity varies with ts
4 结 论
通过分析CFRP约束钢管高强混凝土的工作机制,探讨CFRP约束HSC和CFRP钢管混凝土的主要区别,并基于极限平衡法,推导CFRP约束钢管HSC轴压短柱极限承载力理论计算模型,并分析计算结果随CFRP层数和钢管壁厚的变化规律,所得结论如下:
1) 与CFRP约束钢管混凝土相比,CFRP约束钢管HSC轴压短柱破坏过程中,弹性阶段较长,而弹塑性阶段较短,且多表现为压缩剪切破坏。
2) 与CFRP约束钢管混凝土相比,CFRP约束钢管HSC中核心HSC的侧向膨胀的完全性不如普通混凝土,且侧压效应系数相比也较小。
3) 两类预测承载力模型与试验实测值的对比得出:N
∶N
的平均值为1.05,标准差为0.066,变异系数为0.063;N
∶N
的平均值为0.978,标准差为0.035,变异系数为0.036。该计算结果验证了本文理论模型的正确性。4) 随着CFRP层数的增加,本文理论模型所得极限承载力提高幅度较为明显;对于CFRP约束钢管HSC轴压短柱极限承载力的提高,厚壁钢管表现出较大优势。
