数学实验教学：提升数学素养的重要途径

赵德琴

[摘  要] 数学核心素养是课程标准的目标，也是时代发展对人才的要求. 教学中注重加强学生动手实践能力，在操作体验中培养学生观察分析和逻辑思维能力，借此提升其数学核心素养.

[关键词] 数学实验;数学素养;动手实践

《义务教育数学课程标准》提出了培养学生十大数学素养的要求，围绕这十大素养，教师的教学也需要做出相应的改变. 教学不再仅仅是单纯地传授数学知识，而是在数学课堂上传授数学方法，渗透数学思想，提升数学素养. 数学素养是学生通过学习数学知识，学会运用数学知识去解决问题，并能用数学思想去看待世界，形成正确的情感态度价值观，比起生硬的知识，更强调情感的诉求.

那么如何在教学中去提升学生的数学素养呢？很明显教师需要改变教学的策略和教学方法，需要去思考学生感兴趣的是什么？应该学什么？怎样学？学生更加感兴趣的不是直接获得知识，而是如何获得知识的过程，在过程中去分析和思考，产生获得知识的成就感. 因此教师应该重视数学实验的教学，让学生在“做中学”，在体验和感受中收获成长. 笔者将结合自己的教学实践和思考，谈一谈如何进行数学实验教学，提升数学素养.

认识数与代数

数与代数是数学中的重要内容，涉及数的认识、方程、函数等等，学好这部分内容是提升数学学习效果的基础. 通过学习数的运算、数量关系的变化以及函数、方程等内容，培养学生在运算能力和数感方面的核心素养，培养学生运用代数知识解决问题的能力. 在数学实验中，加强学生数与代数的学习和提升他们运用知识的技能至关重要.

案例1 切饼实验

数与代数中的经典问题切饼问题，主要讨论的是切的刀数与饼的块数之间具有怎样的关系. 在生活中学生经常能遇见这类题目，但是如果没有善于思考的能力，就容易被他们忽视. 为了让学生有更深刻的体会，教师可以通过问题进行引导实验.

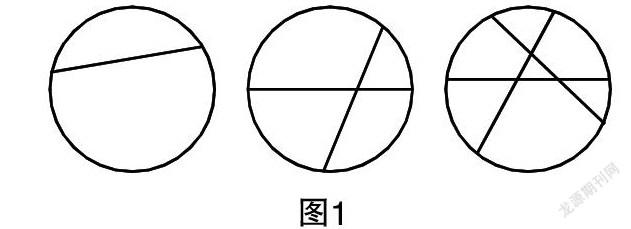
问题1：如图1，图中反映出切1刀、2刀、3刀后，饼有什么变化呢？

生：切1刀，饼被切成2块;切2刀，饼被切成4块;切3刀，饼则被切成7块.

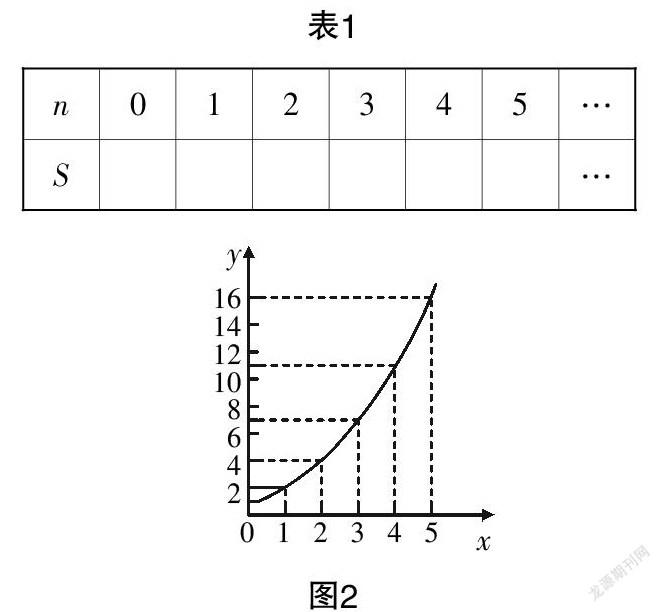
师：同学们应该都有买饼当早饭的经历，那么如果切4刀、5刀，或者n刀，这块饼最多会被切成多少块呢？一下子回答有些困难，那我们先做一个实验，同学们不妨试一试，把结果记在下面的表格里.

（学生以小组为单位开始进行动手操作和记录. ）

师：同学们完成的都很快. 那么下面我们把记录的结果，用坐标表示出来. 根据坐标上切的刀数和饼的块数的关系，你有什么发现呢？

本例中学生通过动手实践操作，记录数据，进而在坐标上呈现数据，使结果一目了然. 通过坐标轴的观察，学生需要运用函数知识建立数学模型，将所切刀数和饼的块数表示出来，有了这个数学模型，随意变化数值，学生都能轻而易举地计算出结果. 在整个操作过程中，学生充分运用了动手能力、观察分析的能力及交流合作的能力，可以说是学生综合能力的运用. 在这个过程中，学生也自然极大地提升了数学素养.

探究几何与图形

几何与图形是初中阶段数学的又一关键知识，需要学生学会认识图形及其运动、平移、转换等等，能够通过学习图形知识，将生活中的实际问题进行图形转换建模，进而解决问题. 解决图形问题既需要空间概念，又需要几何推理能力. 通过动手操作，使学生不仅对图形及其定理有了明确的认识，还培养了他们的应用意识及创新思维.

案例2 探究角平分线的性質实验

探究活动：

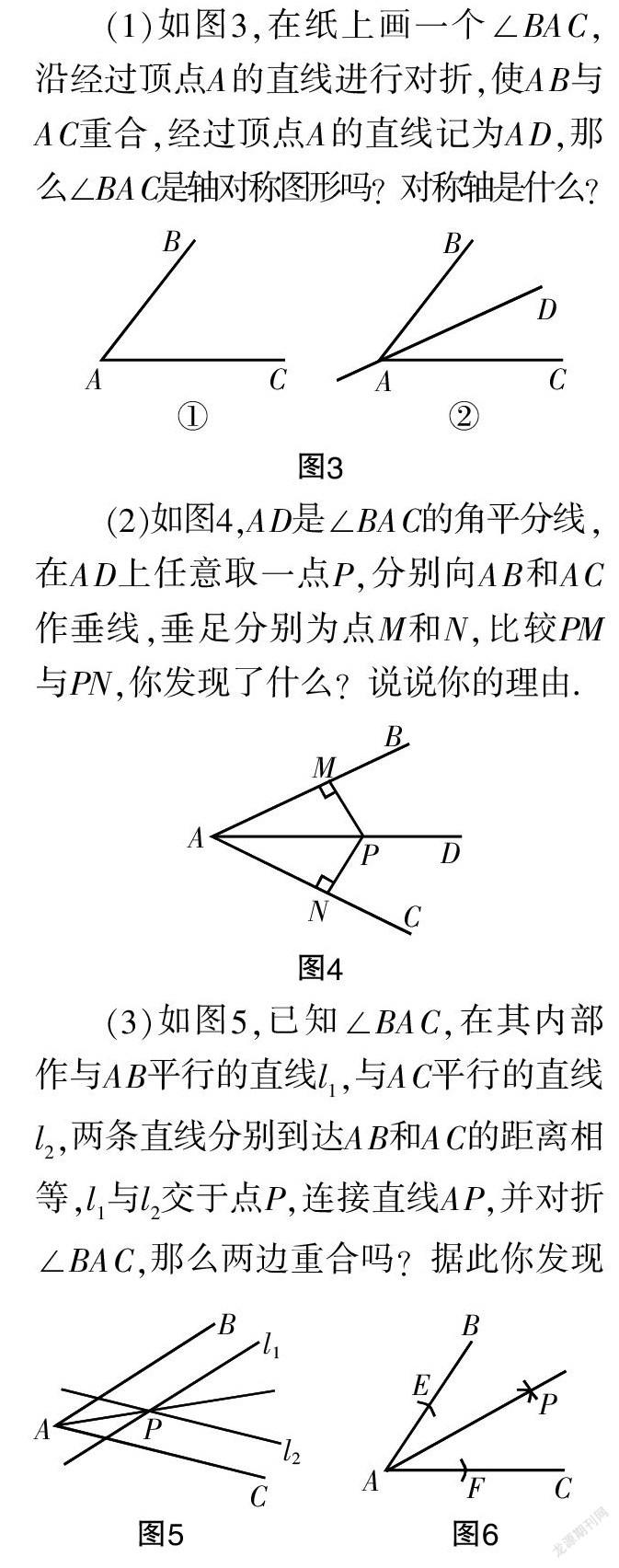
（1）如图3，在纸上画一个∠BAC，沿经过顶点A的直线进行对折，使AB与AC重合，经过顶点A的直线记为AD，那么∠BAC是轴对称图形吗？对称轴是什么？

（2）如图4，AD是∠BAC的角平分线，在AD上任意取一点P，分别向AB和AC作垂线，垂足分别为点M和N，比较PM与PN，你发现了什么？说说你的理由.

（3）如图5，已知∠BAC，在其内部作与AB平行的直线l，与AC平行的直线l，两条直线分别到达AB和AC的距离相等，l与l交于点P，连接直线AP，并对折∠BAC，那么两边重合吗？据此你发现了什么呢？

（4）已知一个角，怎样用直尺和圆规作出它的角平分线呢？

本例通过四个探究活动，逐层推进，引导学生认识并理解角平分线的定义，第一个活动是帮助学生认识什么是角平分线;第二个活动是探究角平分线的性质;第三个活动则采用逆向思维，运用角平分线的性质解决问题;第四个活动是能够通过自己的作图找到角平分线. 经过这四个探究活动，学生从知识掌握到技能运用，全方位地掌握了角平分线这一知识点.

这四个实验活动，涉及实践、思考、分析，调动了学生的综合思维能力，学生并不只是简单地获得了角平分线这一知识，而是在实验的过程中，学会了如何认识这一知识，怎样从直观推理到理性认识，培养了学生的空间概念，提升了数学素养. 在学习几何图形的过程中，教师可以任性一的问题，抽丝剥茧地去引领学生探索知识，并从中感悟数学的方法和思想，体会数学的趣味性.

学会统计与概率

在小学阶段，学生已经初步认识概率与统计. 在初中阶段，学生要学会更加复杂的概率与统计知识. 概率与统计在日常生活中的应用是非常广泛的，通过学习，可以培养学生的数学运算能力、逻辑推理能力等等. 下面以概率知识为例，为了让学生更好地理解概率，笔者设计了如下探究活动.

案例3 摸球实验

（1）准备6个大小相同，质地相同的乒乓球，放在一个不透明的袋子里，其中2个红色、2个黑色、1个白色、1个黄色，摇匀后随意摸取，请问有几种结果？摸到哪种颜色的概率大？哪种颜色的概率小？

（2）摸到一个球，把颜色记下来，再重新放回袋子，重复摸取50次，你觉得会是怎样的结果？进行50次实验，记下结果.

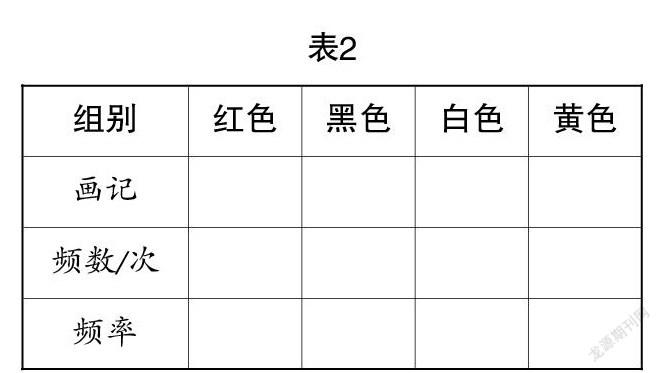
（3）将活动一的实验，通过表格记载下来，并计算频率.

（4）观察上述表格中的频数和频率，你发现了什么？计算各组中的频数之和与频率之和，你又发现了什么呢？

上述实验活动是学生通过自己的实验、数据记录、发现规律进而认识概率的过程. 首先通过活动一学生体会到可能性的大小;接着通过50次的实验，体会频数和频率的关系，对如何计算频率有了初步认识;最后计算频数和频率之和，明确了频数即为实验的次数，频率之和则为1. 学生通过自己的实验活动，经过数据的整理观察和分析，再通过小组的交流，逐渐发现其中的奥秘，理解频率的含义. 概率的知识难度并不是很大，重要的是学生通过实验过程学会方法，在今后的学习中这些方法都将经常可以用到. 通过这样的实验活动，学生认识到数学的定理、知识并不是随意得到的，都具有其深刻的实验基础，引导学生通过理性的眼光去客观公正地看待世界，做到“以理服人”.

以上三个案例只是日常教学中实验活动的冰山一角，大部分的数学知识都可以通过数学实验活动进行讲解和渗透. 新课程改革以来，教师都认识到要加强学生数学活动的体验，但是对于以什么内容为抓手，却常常存有困惑，以至于裹足不前. 首先教师要深刻认识到教育需要培养什么样的人以及怎样培养人. 在这一目标的引领下，相信我们会深知数学课堂怎样让学生“动起来”，参与进来，真正明确学生是学习的主体，一切从学生的实际出发. 只有在实际操作和体验中，学生才能真正感受到知识的魅力，对数学产生兴趣，愿意付出时间和精力去探索交流，收获成功.

总之，教师要改变“一言堂”“满堂灌”的习惯，以问题为导向，开展数学实验活动，培养学生动手操作、观察分析、逻辑推理的能力，在活动中激发学生学习的兴趣，提高他们学习的主动性和积极性，促使他们学会知识和技能，感悟数学思想，从而不断提升数学素养.