时滞位置反馈对一类双边电容型微谐振器复杂振动的控制
2022-03-27尚慧琳董章辉刘智群
尚慧琳, 刘 海, 董章辉, 刘智群
(上海应用技术大学 机械工程学院,上海 201418)
静电微谐振器是微机电系统(micro-electro-mechanical system, MEMS)中最常用的元器件之一,广泛应用于传感器、加速度计、通信和信号处理设备中[1]。对于这类微器件来说,振动微结构的动态特性将对系统的工作性能有直接影响,如微谐振器结构的混沌运动往往导致无规律的输出响应,得不到预期的谐振输出,也容易使振动元件由于疲劳振动而失效[2];又如微结构振动元件过度振动,还容易导致微结构发生吸合现象[3]。因此避免微谐振元件的吸合现象和谐振失稳行为成为保障微谐振器正常运行的两个基本问题。也因此,对微谐振器结构的吸合不稳定现象(微结构的初始位移或速度等初始条件的微小扰动导致微结构的静电吸合),以及混沌等复杂动力学行为的研究成为微谐振器领域研究的热点。Siewe等通过数值方法模拟了一类双极板电容型静电微机械谐振器振动系统的混沌响应,发现参数激励幅值增大会引起混沌。Dantas等[4]研究了由两侧静电电极驱动的微纳米谐振器的混沌动力学行为,发现小的黏性阻尼和间隙不对称性更有利于系统发生混沌振动。Sabarathinam等[5]基于模拟电子电路框架研究了一类双边电容型MEMS谐振器,发现驱动电压的增加易诱发结构混沌振动。在对微结构的吸合不稳定现象的研究上,Ruzziconi等[6]通过试验研究发现单边平行板电容型微谐振器存在吸合不稳定现象;Alsaleem等[7]结合试验和数值模拟研究了一类静电微谐振器动态吸合现象,并基于安全域思想,通过微结构振动系统的安全域侵蚀现象(即安全域边界分形,对应初始条件微小变化导致过度振动乃至系统崩溃[8-9]),诠释交流电压幅值的改变所导致的微结构吸合不稳定现象;Prasanth等[10]基于对非均匀横截面梁式微谐振器系统的定性分析,发现非线性效应对梁结构的不均匀性高度敏感:在大弹性挠度下静电力极易引起微谐振器的吸合不稳定;Ramini等[11]结合理论方法和试验验证研究了MEMS拱在交流电压激励接近第一和第三共振频率发生的吸合不稳定现象及其机制。
为保障微谐振器的正常工作,应对其吸合不稳定和混沌等复杂动力学行为实施有效控制。然而,对于微机电系统来说,由于微谐振器件本身尺寸微小,在结构上直接加载主动控制明显容易造成结构局部发生形变等不良影响,可行性较低。因此多数的控制是在驱动电路上施加。对微谐振器复杂动力学的主动控制引起了广泛地关注,其中控制混沌方面,控制方法及其机理研究较多[12-14]。Haghighi等研究了带有静电力的微机械谐振器的混沌动力学,并提出了一种鲁棒自适应模糊控制算法来控制混沌运动。Tusset等分析了一类静电驱动的双边电容型微谐振器的混沌动力学行为,并通过基于Lyapunov-Floquet变换的状态反馈控制技术将其控制到所需周期性轨道。对吸合不稳定现象的控制研究主要集中在试验仿真和数值模拟方面,如Alsaleem等[15]提出在一类单边平行板电容式微加速度计的驱动直流偏置电压上施加时滞位移反馈和时滞速度反馈来控制系统的吸合不稳定现象,并得到了良好的控制效果;其中时滞反馈控制最早由Pyragas[16]提出用以控制振动系统的混沌行为,并取得了良好的控制效果;后来得到推广应用,成为控制混沌等复杂动力学行为的良好的主动控制方法[17]。然而,对于微结构吸合不稳定的控制机理尚不够明确,相关研究报道较少,仍有待进一步开展。
为此,本文以一类典型双边电容型微谐振器为研究对象,提出通过施加在直流偏置电压上的单通道时滞位移反馈来抑制微结构的混沌运动和吸合不稳定现象,并基于全局分岔理论研究控制的机理。
1 动力学模型和无扰动系统
考虑一类典型的静电双边电容型微谐振器,其简化结构,如图1所示[18],上下两极板为定极板,中间极板本身是静电驱动两端固支梁结构的动极板,简化为中间极板中段黑色矩形所示的等效质量块。考虑振动结构的线性刚度、线性阻尼、非线性刚度和极板间的非线性静电力,并忽略平行板电容的边缘效应,Haghighi等和Mestrom 等建立的动力学模型为

图1 时滞位移反馈控制静电微谐振器系统动力学模型
(1)
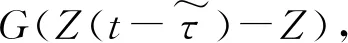
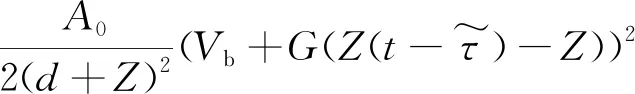
(2)

对系统式(2)引入以下无量纲化变量
(3)
得到无量纲系统
(4)
由于式(2)中阻尼系数、交流电压幅值与直流偏置电压之比以及反馈增益均为小量,因此可引入小参数ε(0<ε≪远远小于1)对式(4)重新进行参数标度,即

(5)
则有
(6)
当时滞量τ=0或增益系数g=0时,时滞反馈项为零,反馈控制式(6)退化为无控制系统;此外,参数α只与结构设计参数有关,而与所施加的驱动电压无关,参数则是直流偏置电压Vb的函数。
当ε=0时,系统式(6)退化为无扰动系统
(7)
式(7)为Hamilton系统,其Hamilton量和势能函数分别为
(8)
(9)
由此可知,系统有无势阱,以及势阱的形态、具体位置以及平衡点个数,均取决于参数α和β。当α=12和β=0.338时,该系统式(7)存在5个平衡点,其中S1(xs,0)和S2(-xs,0)为鞍点,C1(xc,0)、C2(-xc,0)为中心,具有三势阱、且同时存在同宿和异宿轨道,如图2所示。由于本文聚焦于同异宿轨道共存情况下,系统参数引起的同异宿分岔行为及其机制,以及对应的时滞位移反馈控制机理,因此仍按尚慧琳等研究中给定的系统参数取值,具体如表1所示。

图2 α=12和β=0.338时式(7)的相轨线

表1 系统式(2)物理参数取值
2 同宿分岔行为及其控制机制
当式(1)发生同宿分岔时,非常容易诱发混沌现象。本章重点研究同宿分岔引起的混沌运动及其时滞位移反馈控制机制。为此,考虑图2中的一对同宿轨道,其最右侧边缘点T1(xe,0)满足
(10)

φ(-∞)=0,φ(∞)=π
(11)
构造同宿轨道
xh(φ)=a(1-cosφ)+bsinφ
(12)
则对于无扰动系统满足
(13)
得到同宿轨道的精确解析表达式
xh(φ)=xesinφ,
(14)

(15)

(16)
保留式(6)中ε一次方项,将其他含有ε的项当作摄动项,则式(6)成为
(17)
对于施加时滞位移反馈的微谐振器系统式(6),可以将Melnikov函数法推行至时滞受控系统从而获得受控系统的同宿分岔必要条件。为此,时滞反馈须为摄动项,即以时滞反馈控制项不会引起平衡点稳定性的切换为前提,则时滞反馈不会引起系统平衡点的定性改变。其中对于系统式(6)的线性化系统平衡点O(0,0)是稳定的焦点,不会发生稳定性切换。当τ=0时,对于非零平衡点(±xc,0)是稳定的,τ≠0时为考察(±xc,0)邻域的稳定性,设
x=xc+εu+O(ε2),u=O(1)
(18)
(19)
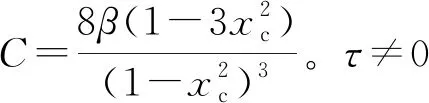
(20)
设λ=iv,代入式(20)分离实虚部,消去正余弦函数项得到
(21)

(22)
则式(21)有两个不相等的正根ω+和ω-,其中ω+>ω-;根据局部分岔理论,系统式(4)发生Hopf分岔的时滞临界值为
(23)
M(t0)=-μI1±2βγI2cos[ωT0(φ)]+I3sin[ωT0(φ)]+8βτgI4
(24)
其中
F(φj,ηj)和E(φj,ηj)分别为第一类和第二类椭圆积分,j=2,3。
当
(25)
时,Melnikov函数存在简单零点,这是系统发生同宿分岔的必要条件。将参数还原为原系统参数,则得到了受控系统(6)的同宿分岔条件,即
(26)
显然,式(26)中时滞量τ=0时即为无控制系统的同宿分岔条件。在本文给定参数情况下,I1和I4表达式中的被积函数在(0,π/2)上的积分值显然大于0,即有I1>0和I4>0;因此,根据式(26),正的反馈增益系数下,时滞量在一定范围内单调递增(不超过平衡点稳定性切换临界时滞),则时滞位移反馈能够提高系统式(6)的同宿分岔的交流电压门槛值,其中在表1系统参数取值下,无控制的原微谐振器振动系统发生同宿分岔的交流电压临界幅值为0.152 V。给定增益系数g=0.18,同时选取相对较小的时滞量,即从均匀增大到0.25,数值模拟得到的引起微结构混沌振动的交流电压临界幅值和理论预测的同宿分岔交流电压阈值对比如图3所示,二者比较吻合,这说明时滞位移反馈能够有效抑制系统发生的同宿分岔,从而为控制由同宿分岔引起的混沌现象提供依据。

图3 g=0.18时交流电压同宿分岔门槛值随τ的变化

图4 当g=0.18和ω=0.5时,系统式(4)响应随交流电压幅值变化

图5 当VAC=0.17 V,ω=0.5和g=0.18时,不同时滞下系统(4)的动力学行为
3 异宿分岔行为及其控制机制
时滞位移反馈微谐振器振动系统式(2)同时还存在着异宿轨道。而异宿轨道的破裂同样破坏系统的动完整性。根据尚慧琳等和Wang等的研究,在无控制系统中,微结构的吸合不稳定现象可归因于系统发生异宿分岔,这是有别于第2章混沌现象的另一种复杂动力学行为。本章在此基础上集中讨论系统的异宿分岔行为和机制,以及时滞位移反馈控制该现象的机理。
与同宿轨道一样,本系统的异宿轨道也无法直接表达成时间T的显函数。为了得到异宿轨道的精确解析形式,进而在此基础上讨论异宿分岔条件,与上节类似,引入中间变量,假设
x(φ)=±xscosφ
(27)
根据式(11)和式(13)得到异宿轨道的精确解析表达
xHetero(φ)=±xscosφ,
(28)

(29)

同样,可将Melnikov函数法推行至时滞控制系统来获取受控系统发生异宿分岔的必要条件,其前提是原线性化系统仍不会因时滞项的出现发生平衡点稳定性的切换。为此,考察平衡点(0,0)邻域的稳定性,设
x=0+εu+O(ε2),u=O(1)
(30)

(31)
由式(31)可知,时滞反馈项的出现不会引起线性化系统平衡点的稳定性发生切换。因此时滞量可作为扰动项进行二阶Taylor展开,其相应Melnikov函数为
(32)
其中
根据Melnikov函数存在简单零点得到时滞位移反馈控制下交流电压幅值的门槛值为
(33)
由于根据J4表达式中被积函数在积分区间均大于零,显然有J4>0,因此,由式(33)可知,在正的反馈增益系数下交流电压的门槛值会得到提高。
给定时滞增益系数g=0.18,引起异宿分岔的驱动交流电压临界幅值随时滞量的变化的理论预测如图6中直线所示,而对无量纲化时滞反馈控制系统式(4)进行数值模拟,得到的不同时滞量下微结构发生吸合不稳定现象的临界交流电压幅值如图6中离散的点所示。在无时滞反馈控制情况下,系统发生异宿分岔的交流电压幅值门槛值理论预测为0.251 V,这与图6中数值结果相一致。随着时滞量的增大,在较小的交流电压幅值下(即满足VAC/Vb≤0.1时),数值和理论结果完全吻合。继续增大时滞量,当VAC/Vb>0时,数值和解析结果开始出现少量偏差,这主要是因为式(33)中的解析结果是基于式(5)将VAC/Vb设定为小参数的假设得到;尽管如此,交流电压临界幅值仍然随时滞量增大,与理论分析定性结果一致。式(33)和图6中数值与理论结果的对比为时滞位移反馈抑制异宿轨道破裂,进而抑制异宿分岔引起微结构吸合不稳定现象提供了理论依据。此外,根据图6,当τ=0时,同宿分岔交流电压幅值0.152 V小于交流电压异宿分岔门槛值0.251 V,因此无控制系统(即τ=0时)并不发生吸合不稳定现象;再对比第2章同电压无时滞系统的混沌动力学行为(见图5(a)、图5(b)和图5(c)的相图和Poincáre截面和谱分析),这说明在本系统中混沌运动与吸合不稳定现象由于成因不同(前者归因于同宿分岔,后者源于异宿分岔),并不同步发生。

图6 g=0.18时交流电压异宿分岔门槛值随τ的变化

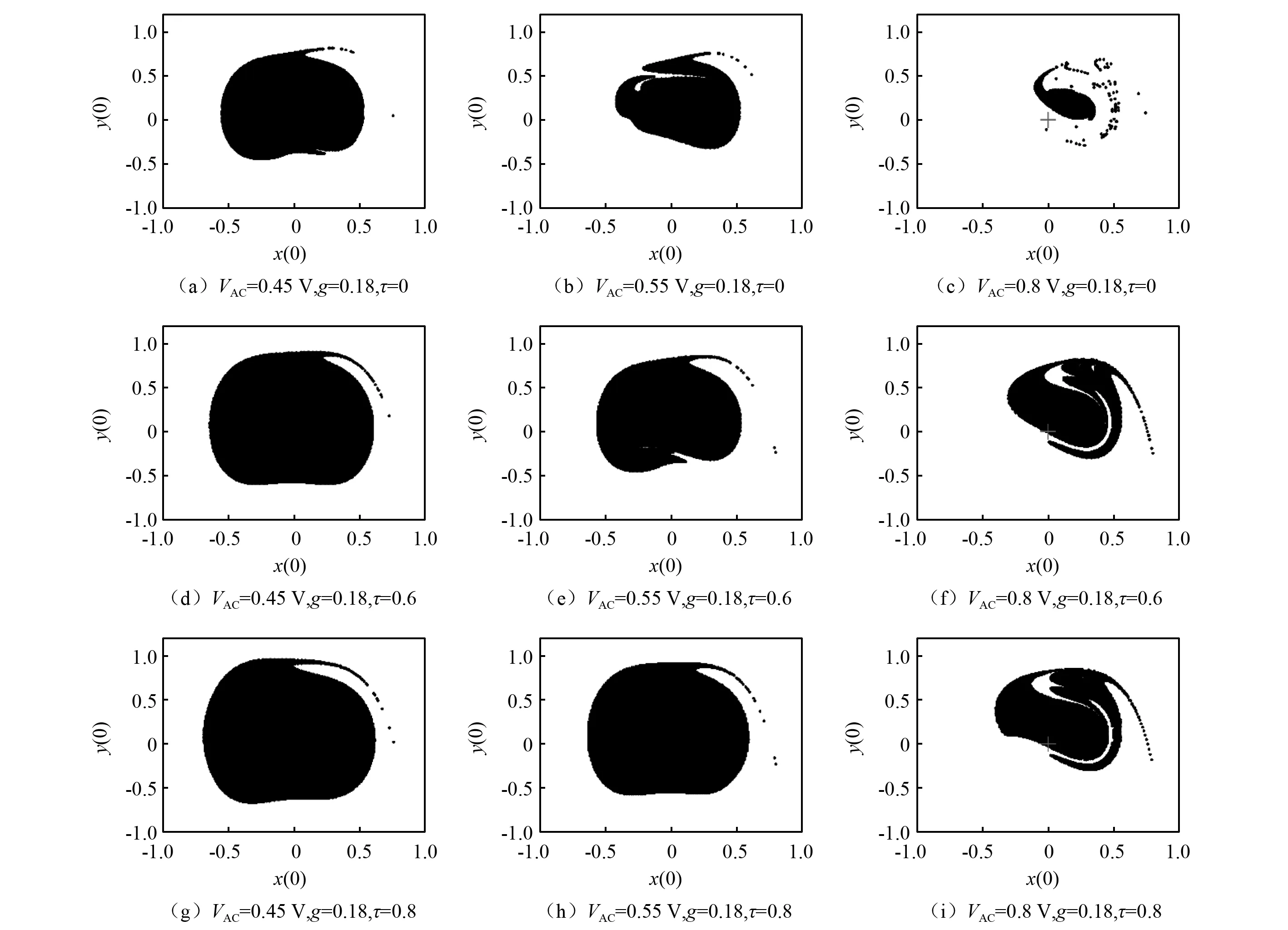
图7 当g=0.18时,不同的交流电压幅值下系统式(4)安全域随时滞量的演变
4 结 论
本文以一类双边电容型微谐振器振动系统为研究对象,具体选取同异宿轨道共存的情况,对系统施加时滞位移反馈来抑制系统的混沌和吸合不稳定等复杂动力学行为,并研究其控制机理。主要得到以下结论:
(1) 本系统中,混沌和吸合不稳定这两类初值敏感性现象并不同时发生,归因于两类不同的全局分岔:随着交流电压幅值的增大,同宿分岔和异宿分岔相继被诱发,先后引起微结构的混沌振动和吸合不稳定。
(2)当反馈增益系数大于零时,随着时滞量的增大,时滞位移反馈控制不仅能够抑制微结构混沌振动,还能够有效地抑制微结构的吸合不稳定;其控制机理可以理解为通过改变单控制参数(即时滞量)来提高系统发生同宿和异宿分岔的交流电压门槛值。
上述结论为揭示非线性系统中混沌现象和安全域分形这两类典型的全局失稳行为的机制及其控制机理研究提供一定的理论依据;并在保障谐振器振动系统的动完整性和设计研制更加精密的静电驱动微器件方面具有潜在的应用价值。本文为了聚焦刚度和静电力非线性引起的微谐振器复杂振动,对双边电容型微谐振器,基于一定的理想化假设,采用了集总参数型简化模型。在后续研究中,将对两端固支微谐振梁的不同位置的纵向振动,考虑尺寸效应、边界条件、振动模态和刚度非线性等因素,建立更实际的微谐振梁动态方程。
