两类串列圆柱涡激振动的质量比效应
2022-03-27杜晓庆唐晨馨吴葛菲
杜晓庆, 唐晨馨, 赵 燕, 吴葛菲, 杨 骁
(1.上海大学 力学与工程科学学院,上海 200444; 2. 台州学院 建筑工程学院,浙江 台州 318000)
大长细比的柱群结构在桥梁工程、海洋工程中有广泛应用,如并列吊索、并列斜拉索及海洋立管等[1-4]。受上游圆柱尾流的干扰,下游圆柱的涡激振动比单圆柱的更为剧烈,进而影响结构的使用寿命。以往研究表明:质量比是圆柱涡振的重要影响因素之一[5-12],而双圆柱涡激振动的质量比效应尚待进一步研究。
对于单圆柱的涡激振动,谷家扬等和陈正寿等发现单圆柱振动锁定区间会随着圆柱质量比的增大而减小。Mittal等发现:低质量比(质量比为4.25)的单圆柱会出现“弱锁定”现象(即振动频率与自振频率的频率比小于1的振动锁定现象),这与较高质量比时(质量比为25)仅出现的常规振动锁定现象(频率比为1)不同。Khalak等在质量比0.36~25.00内,通过试验研究指出:质量比对单圆柱涡激振动的流场结构及振幅有显著影响。

圆心间距对串列双圆柱的涡激振动也有明显影响。郭晓玲等[23]在Re=150,柱心间距比为3、5、8,质量比5、10、20条件下,研究了上游圆柱固定时,下游圆柱的振动响应特性;研究表明,不同间距比会导致下游圆柱振动锁定区间的发生变化。Brika等[24]对柱心间距比为10~25的双圆柱涡激振动进行了试验研究,结果表明:下游圆柱振动的尾流结构和耦合机理与上、下游圆柱之间的间距有关。邹琳等[25]对Re=100,圆柱的柱心间距比为2~5的串列双圆柱涡激振动进行数值模拟,发现随着间距比的增大,下游圆柱的振动对上游圆柱的影响减弱。Papaioannou等[26]对雷诺数Re=160、3组间距比(柱心间距比为2.5、3.5和5.0)的串列双圆柱涡激振动进行数值模拟,结果表明:随着圆柱的柱心间距比的减小,上游圆柱的振动锁定区间的范围增大;当圆柱的柱心间距比为5时,上游圆柱几乎不受下游圆柱的影响。及春宁等[27]也得到了类似结论。Sumner[28]将静止串列双圆柱的绕流流态分为单一钝体、剪切层再附和双涡脱3种,并把剪切层再附流态到双涡脱流态转变的间距比称为临界间距比。Huhe-Aode[29]提出雷诺数为100时的串列双圆柱涡激振动的临界间距比为4.5~5.0,其结果稍大于数值模拟的结果[30]。Sharman等[31]采用数值模拟方法则发现串列双圆柱涡激振动的临界间距比为3.75~4.00。
研究双圆柱涡激振动质量比效应的文献很少,已有研究是针对双圆柱均仅在横流向振动或上游圆柱静止而下游圆柱振动的情况。Tofa等[32]发现下游圆柱横流向振幅随着上游圆柱质量比的降低而减小。Jiang等[33]分析了质量比分别对上、下游圆柱涡激振动的耦合效应。杨骁等[34]在上游圆柱静止条件下,研究了质量比对下游圆柱振动特性和流场结构的影响规律。目前尚未见到研究上、下游圆柱均可做顺流向和横流向振动的串列双圆柱涡激振动质量比效应的文献。
本文采用CFD(computational fluid dynamics)数值模拟方法,结合动网格技术,对两类串列双圆柱涡激振动的质量比效应进行研究。参考Mittal等和Ravi等[35],考虑计算成本,本文在低雷诺数Re=100的层流条件下进行数值模拟计算;圆柱质量比分别取2、10和20,上、下游圆柱的柱心间距比为4,圆柱可作顺流向和横流向两自由度运动。重点分析了圆柱振幅、振动频率比、柱间距和流场结构随质量比和折减速度的变化规律,并与上游圆柱静止的串列双圆柱涡激振动的结果进行对比,研究了两类串列双圆柱涡激振动的质量比效应及流场结构的差异,探讨了串列双圆柱发生涡激振动时的流场驱动机制。
1 数值方法与计算模型
1.1 数值方法
1.1.1 流体域
本文针对二维不可压缩流体,采用Ansys Fluent16.0软件进行计算,流体域控制方程为连续方程和动量方程,采用SIMPLEC法求解压力与速度的耦合,选择二阶迎风离散格式求解动量方程。
1.1.2 结构域
圆柱在顺流向和横流向的振动方程分别为
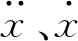
1.1.3 流固耦合的实现
本文利用动网格技术,结合UDF(user-defined function),采用四阶Runge Kutta法求解圆柱的振动控制方程,实现圆柱流固耦合的数值模拟,详细的介绍可参考杨骁等的研究。
1.2 计算模型
图1为本文所研究的两类串列双圆柱的计算模型,其中圆柱的涡激振动被简化为弹簧-阻尼器系统。图1(a)中的上、下游圆柱均可作横流向和顺流向的两自由度振动,下文简称为Cy1_2DOF,其中Cy1代表上游圆柱。图1(b)中的上游圆柱静止、下游圆柱可作横流向和顺流向的两自由度振动,下文简称为Cy1_Fixed。脚标“1”、“2”分别代表上、下游圆柱。

图1 双圆柱涡激振动系统简图

图2为本文的计算域,由半圆弧域和矩形域组合而成,双圆柱圆心连线中点处为坐标原点O,串列圆柱的阻塞率为1.67%。流体为沿x方向的均匀来流,入口采用速度入口边界条件,距离原点30D;出口采用自由出流边界条件,距离原点35D;上、下侧壁面采用对称边界条件,距离原点30D;圆柱表面采用无滑移壁面边界条件。
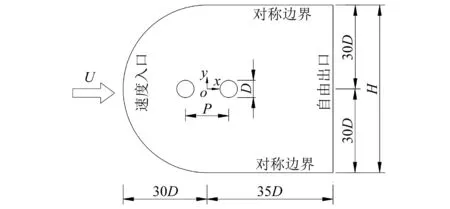
图2 计算域和边界条件
图3为网格划分方案,圆柱近壁面采用结构化网格(见图3(c)),近壁面径向最小网格尺寸为(4×10-4)D。此外,圆柱在图3(a)所示的半径为5.75D的白色虚线圆内振动。本文采用了与Ravi等和Mysa等[36]的研究类似的结构化与非结构化混合设置的计算网格方案。距离圆柱0.25D厚度内的近壁面处区域采用结构化网格,白色圆形虚线内的其余区域,采用非结构化网格(见图3(b));白色虚线外的区域采用结构化网格。

图3 网格划分方案
2 模型验证
为获得可靠的结果,首先分析静止单圆柱的绕流,考虑其周向网格数量、无量纲时间步和阻塞率等参数对数值结果的影响,并与已有文献的研究结果进行对比。然后针对单圆柱涡激振动进行数值模拟,选用了3组计算模型,考虑了不同的网格数量,验证了网格无关性。最终采用的计算模型和计算参数,其检验和结果验证工作详见杨骁等的研究。
此外,为确保该计算模型及参数对串列双圆柱涡激振动的计算结果的合理性和可靠性,Re=100、柱间距为5.5D、质量比m*=10、折减速度Ur=3~13,针对圆柱均可作双自由度振动的串列双圆柱涡激振动进行数值模拟结果的验证。图4中给出了Prasanth等[37]、Chung[38]以及本文的上、下游圆柱的横流向振幅Ay/D随折减速度Ur的变化曲线。从图4可见,本文计算结果与文献结果吻合良好。综上所述,本文采用的计算模型、计算方法及计算参数具有较高的可靠性和较好的精确性。
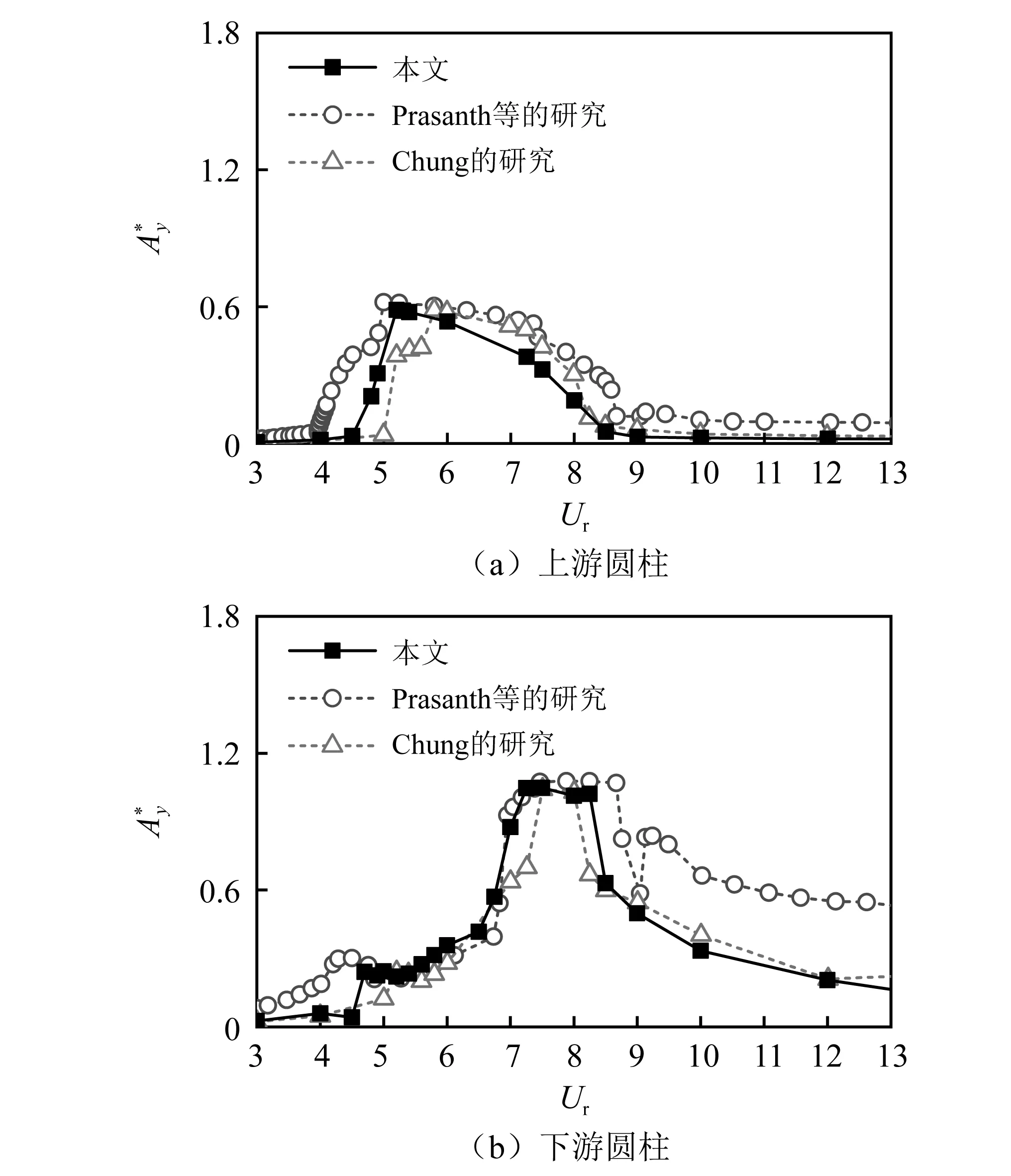
图4 双圆柱涡激振动结果验证(Re=100,m*=10,P/D=5.5D)
3 计算结果及分析
3.1 振动特性
3.1.1 横流向最大振幅

由图5(a)可见,在Cy1_2DOF工况下,上游圆柱的横流向振幅均随着折减速度的增大呈先增大后减小的趋势;此外,随着质量比的增大,上游圆柱的起振速度及最大振幅对应的折减速度有所增大。
图5(b)给出了两类串列双圆柱下游圆柱的横流向振幅随折减速度的变化情况。与Cy1_Fixed工况对比可知,当质量比相同时,上游圆柱的振动会增大下游圆柱的横流向振幅及最大振幅对应的折减速度;随着质量比的增大,在同一折减速度下,下游圆柱的横流向振幅减小;值得指出的是,在m*=2时,即使在较大的折减风速下,下游圆柱仍存在较大的横流向振幅。

图5 圆柱横流向最大振幅随折减速度的变化
3.1.2 顺流向最大振幅
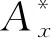
由图6可知,上、下游圆柱的顺流向振幅与横流向振幅相比较小;对于上游圆柱而言(见图6(a)),3种质量比下,上游圆柱横向振幅极值均发生在Ur= 6时,且随着质量比的增大横流向振幅极值减小。图6(b)为不同质量比下两类串列双圆柱顺流向振幅随折减风速的变化曲线。由图6(b)可知,上游圆柱的振动同样会增大下游圆柱顺流向振幅及最大振幅对应的折减速度。随着质量比的增大,下游圆柱的顺流向振幅逐渐减小。此外,当m*=2时,两类串列双圆柱下游圆柱的顺流向振幅均在不同折减风速下出现两个振幅极值。
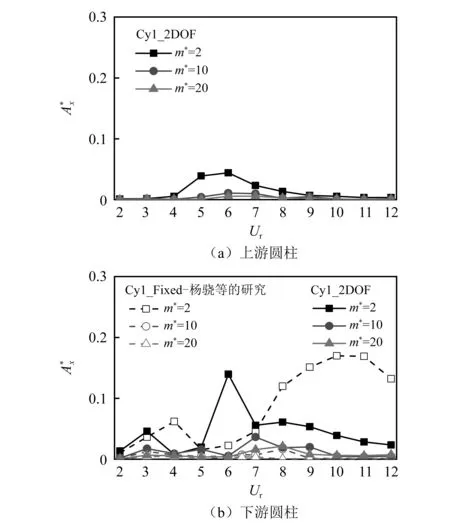
图6 圆柱顺流向最大振幅随折减速度的变化
3.1.3 振动频率比

图7 横流向振动频率比随折减速度的变化
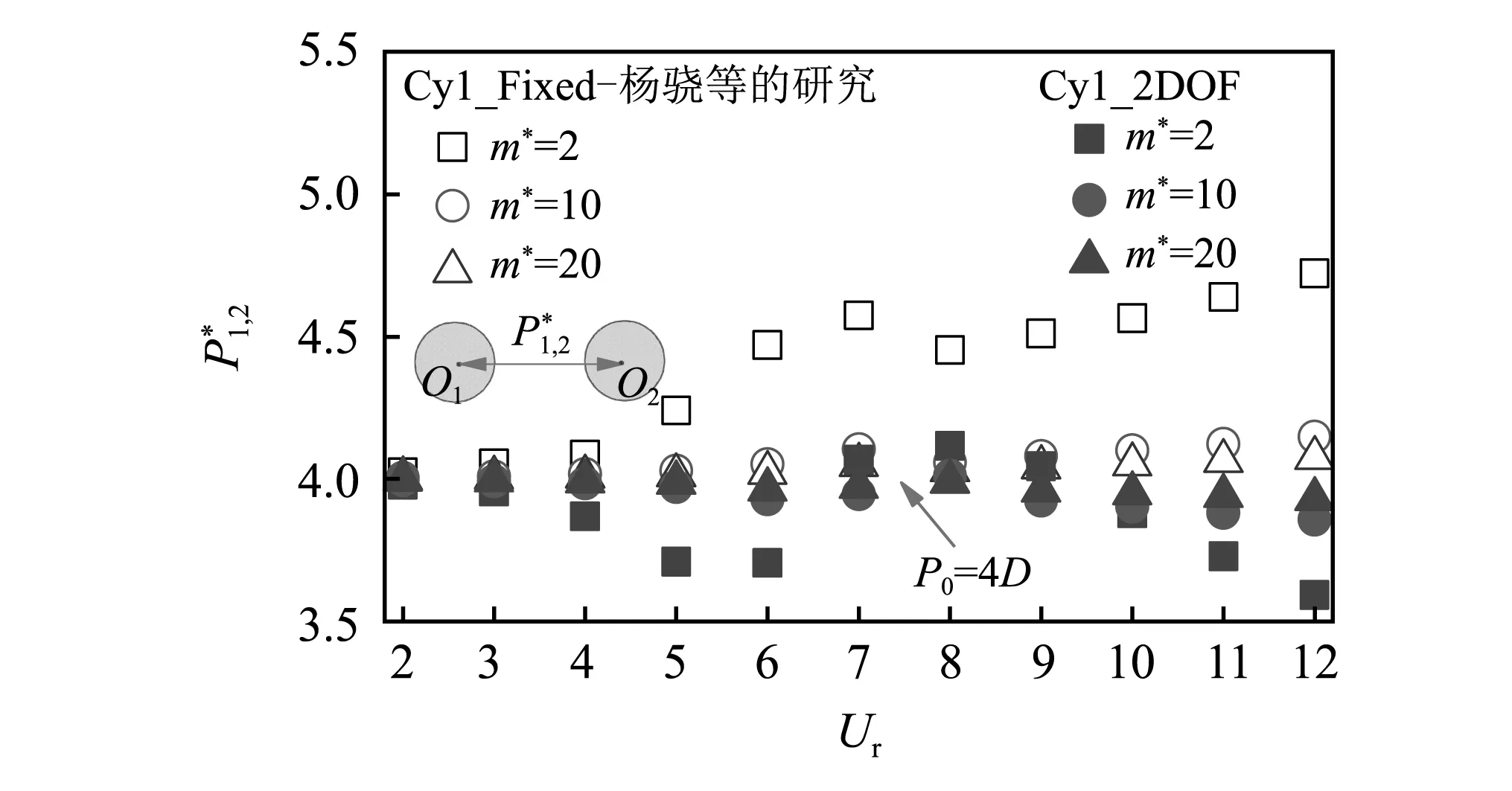
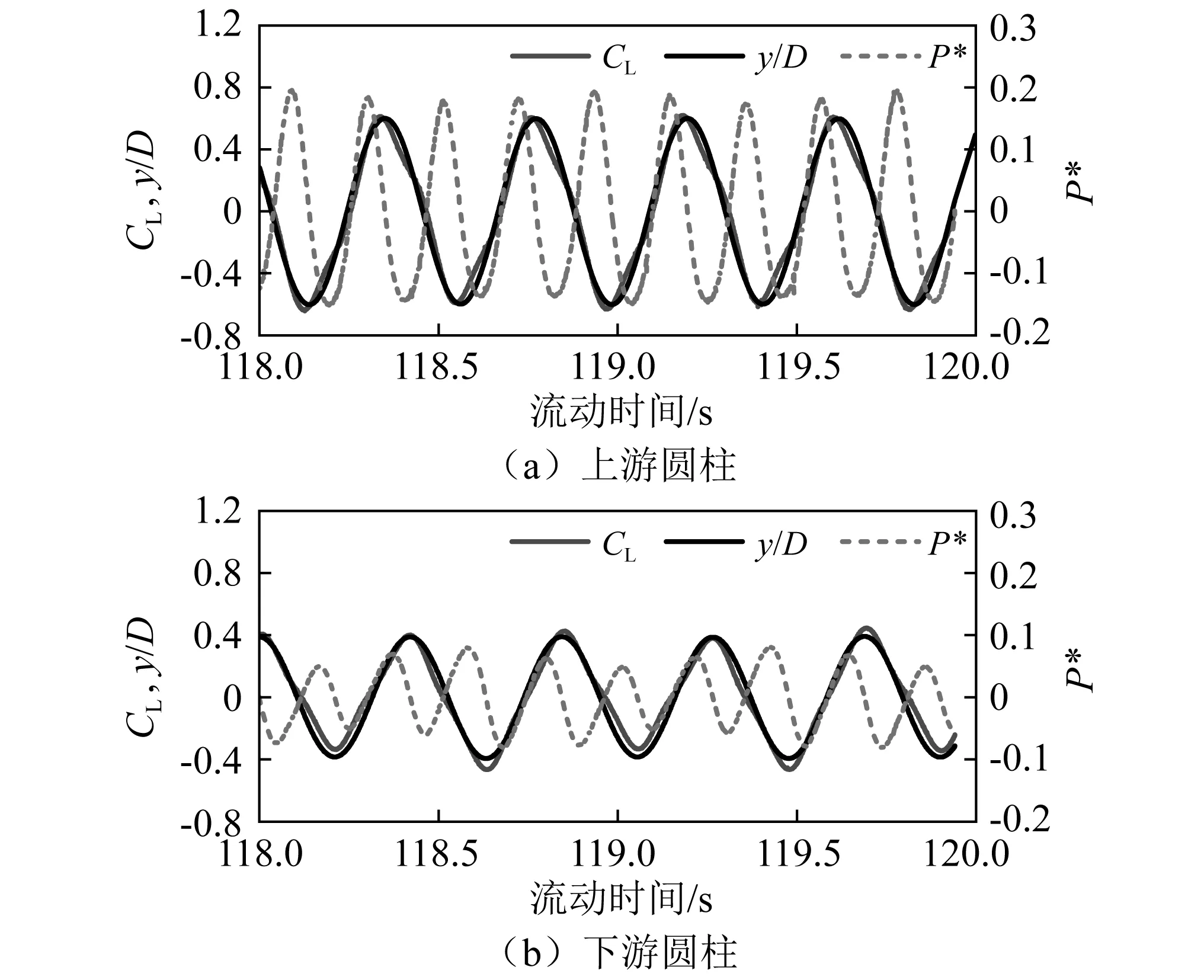
可见,对于Cy1_2DOF工况,当质量比为2时,上、下游圆柱均在5 3.1.4 两圆柱柱心间距比 式中,Xmax、Xmin分别为上、下游圆柱的柱心在顺流向最大位移和最小位移。 图8 串列双圆柱柱心间距比随折减速度的变化 3.2.1 流场结构 图9给出了Cy1_2DOF工况的串列双圆柱在典型折减速度下的瞬时涡量图。可见,3种质量比的串列双圆柱均存在3种类型的涡脱模态,即“2S”涡街模态、不规则涡街模态和平行涡街模态。在振动锁定区外,会出现“2S”模态;而在振动锁定区内时,则会出现不规则涡街模态和平行涡街模态。 图9 串列双圆柱的尾流模态(Cy1_2DOF) 当尾流呈现为平行涡街模态时,不同质量比的下游圆柱尾流结构有着明显的差异。质量比为2时,从下游圆柱同一侧先后脱落的旋涡在尾流有首尾相连的现象,而质量比为10和20时这种现象不明显。 3.2.2 流致振动的能量输入机制 为了进一步揭示串列双圆柱涡激振动的流固耦合机理,结合双圆柱的升力系数与振动位移时程、瞬时能量输入以及瞬时压强分布等方面进一步探讨其流固耦合机制。 基于本文的研究结果,串列双圆柱流致振动的能量输入机制没有明显的质量比效应,3种质量比串列双圆柱的流致振动均具有类似的能量输入机制。因此,本文针对Cy1_2DOF的工况,分析了m*=10、处于频率振动区内的折减速度分别为6和8的两个工况为例,分析其在振动过程中的能量输入及流固耦合机理。其中,Ur=6对应上游圆柱横流向振幅最大时的折减速度;而Ur=8时下游圆柱横流向振幅最大。此外,定义P*=CL(t)v(t)/U为在单位时间内,流体对圆柱横流向振动所作的无量纲功,其中:v(t)为圆柱横流向振动速度;P*为正表示流体对圆柱作正功,反之作负功。 (1)旋涡撞击机制 在双圆柱均处于振动锁定区、且上游圆柱横流向最大振幅大于下游圆柱横流向最大振幅时发生此流固耦合现象,同时串列双圆柱尾流呈不规则涡街模态。 图10给出了质量比为10、折减速度Ur=6时上下游圆柱的升力系数、横流向位移及能量输入的时程曲线。可见,上下圆柱横流向位移随时间呈现同频率周期性变化,在一个振动周期内升力及能量输入随时间变化趋势相同,升力系数与横流向位移基本同相位。当流体对圆柱作正功时,振幅逐渐增大至峰值;当流体对圆柱作负功时,圆柱振幅则逐渐减小。与横流向振幅较小的下游圆柱的振动周期相比,流体对上游圆柱做功较大,即P*峰值的绝对值更大。 图10 升力系数、横流向位移及能量输入时程(m*=10,Ur=6,Cy1_2DOF) 进一步对瞬态涡量图和瞬时风压分布图(见图11)的分析发现:从上游圆柱脱落的旋涡均会与下游圆柱发生撞击,分解成两个子涡从下游圆柱的上、下两侧通过,使下游圆柱负压强度减小,导致下游圆柱的振动被抑制,并在下游圆柱尾流中形成稳定的不规则涡街模态,如图11所示。 图11 下游圆柱的升力系数、横流向位移、能量输入(m*=10,Ur=6,Cy1_2DOF) (2)旋涡融合机制 在上、下游圆柱均处于振动锁定区、且上游圆柱横流向最大振幅小于下游圆柱的情况时发生此流固耦合现象,尾流呈现平行涡街模态。 图12给出了质量比为10、折减速度Ur=8时上、下游圆柱的升力系数、横流向位移及能量输入的时程曲线。可见,上、下游圆柱的位移时程相位差约为90°,即上游圆柱在平衡位置(横流向瞬时位移为0)时,下游圆柱振动到最大位置(横流向位移最大正值或最大负值)。每一个振动周期内的上、下游圆柱升力系数、横流向位移及能量输入随时间均稳定变化,上、下游圆柱横流向位移呈现单一周期变化。相较于横流向振幅较小的上游圆柱,流体对下游圆柱做功更大,即P*峰值的绝对值更大。 图12 升力系数、横流向位移及能量输入时程(m*=10,Ur=8,Cy1_2DOF) 基于对瞬态涡量图和瞬时风压分布图(见13)的分析发现,从上游圆柱上、下侧脱落的旋涡均会与下游圆柱同侧卷起的旋涡融合,增强下游圆柱那一侧的负压强度,促进下游圆柱的振动,并在下游圆柱尾流中形成稳定的平行涡街。 对于Cy1_Fixed的串列双圆柱,同样存在旋涡撞击和旋涡融合的流固耦合机理,但发生的条件与Cy1_2DOF的不同。在Cy1_Fixed工况中,旋涡撞击的流固耦合机理在下游圆柱的振动锁定区外出现,旋涡融合的流固耦合机理在下游圆柱的振动锁定区内出现;而Cy1_2DOF工况中,旋涡撞击和旋涡融合两种类型的流固耦合机理均在下游圆柱的振动锁定区内发生。 图13 下游圆柱的升力系数、横流向位移、能量输入(m*=10,Ur=8,Cy1_2DOF) (1) 在低雷诺数下,质量比对两类串列双圆柱的振动响应均具有显著的影响,圆柱的质量比越小,其涡激振动的最大振幅越大;相同的质量比下,相较于静止的上游圆柱,运动的上游圆柱能激发下游圆柱发生更大的横流向振动。 (2) 质量比对上、下游圆柱均可作两自由度振动的串列双圆柱的振动频率比影响明显。3种质量比下,上游圆柱振动时的上、下游圆柱均存在明显的振动锁定区间,且低质量比时会发生振动频率与自振频率比小于1的“弱锁定”现象,但上游圆柱静止时的下游圆柱不存在明显的振动锁定区。 (3) 质量比对两类串列双圆柱在振动稳定后的间距比均有明显作用。质量比越大,上、下游两圆柱的柱心间距比越靠近初始间距比。对于上游圆柱静止的串列双圆柱,顺流向圆柱柱心间距比普遍大于初始间距比;对于上游圆柱振动时的串列双圆柱,圆柱柱心间距比普遍小于初始间距比。 (4) 质量比对两类串列双圆柱的尾流结构影响不大,3种质量比的两类串列双圆柱均存在“2S”涡街模态、不规则涡街模态和平行涡街模态3种涡脱模态。对于上游圆柱振动和上游圆柱静止的串列双圆柱均存在旋涡撞击和旋涡融合的两种耦合机制,但发生的条件不同。 需要说明的是,本文的工作主要是在低雷诺数层流下,澄清两类串列双圆柱涡激振动的质量比效应,加深对双圆柱涡激振动现象物理本质的认识。而在实际工程中,结构往往处于高雷诺数湍流环境下;因此,串列双圆柱流致振动的雷诺数效应也是今后值得研究的方向。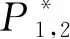
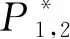
3.2 流场结构与流固耦合机理




4 结 论
