古筝弦-码结构的三维动力学分析与试验验证

邓小伟， 余征跃， 姚卫平， 周 力

(1. 上海交通大学 船舶海洋与建筑工程学院，上海 200240； 2. 上海民族乐器一厂，上海 201101)

古筝是中国独特的、重要的民族乐器之一。它的音色优美、音域宽广、演奏技巧丰富，具有相当强的表现力，因此深受广大人民群众的喜爱。同时它也承载了传播中国民族文化的重任[1]。随着当今科技的迅猛发展，西方乐器在制作规范、声音品质控制以及稳定性等方面都非常成熟，而我国民族乐器古筝由于相关理论研究的缺乏，目前整体相对落后，主要表现在：结构设计缺少科学指导，结构不稳定；制作方式和手段相对传统、落后，制琴质量无法保证[2-4]。因此对于民族乐器古筝的理论研究显得尤为重要[5-8]。

古筝的弦-码结构是其演奏发声过程中的主要振动及传导系统，同时也是影响古筝发声特性的最主要部分[9]。为此对古筝弦-码结构振动特性的研究是了解古筝发声原理并为其结构声学设计提供理论依据的关键性工作。总结相关乐器的弦振动研究，杨健[10]回顾了琴弦研究的发展，讨论了达朗贝尔的弦振动方程，用理想拨弦模型分析了拨弦振动的轨迹、触弦点对音色和音量的影响等；李云芳[11]利用弦振动的基本方程推导分析了使用平面锤、凸面锤和细棒敲击扬琴弦时的振动方程，通过分析n次谐波衰减的快慢，得出不可使用细棒；Mandal等[12]对考虑柔性音板下的弦-板协调振动特性进行研究，给出了板厚、位置、质量等对弦-板振动特性的影响，并给出了最佳参数选择；Taguti[13]利用弦振动方程建立sawari的弦振动模型，分析了弦端在振动中触弦点变化致使发出独特音色的理论依据。这些研究都体现了弦振动特性对乐器声音表现的重要作用，但目前针对古筝这类以弦-码结构作为振动传导系统的乐器，对其相关振动特性的研究相对缺乏。文献[14]将古筝的弦-码结构简化为平面问题，初步建立了古筝弦振动通过琴码传递到面板的动力学模型，并进行数值计算和试验验证，很好的解决了古筝声振特性研究中弦-码结构的理论模型建立问题。然而将其简化为平面问题，就无法体现古筝琴码双码脚设计对古筝声振特性的影响及古筝演奏过程中不同拨弦方式对古筝发声的影响[15-16]。为此在考虑古筝琴码双码脚的情况下建立古筝弦-码结构的三维动力学模型，并分析不同拨弦角度时各码脚法向作用力的变化规律及对古筝发声的影响显得十分必要。

综上所述，本文首先研究了古筝琴弦的振动，并建立弦振动的动力学模型；在此基础上建立古筝弦-码结构的三维动力学模型，并根据不同的演奏拨弦方式，利用MATLAB软件数值计算了不同拨弦角度下琴码各码脚的法向作用力，并进行试验验证；最后根据数值计算以及试验测量结果分析了各码脚作用力的变化规律以及对古筝发声的影响。

1 古筝弦振动的简化模型

古筝的琴弦是两端固定，中间利用琴码顶在古筝面板上的，演奏者通常以拨弦的方式让琴弦获得初始状态后自由振动。虽然琴码在弦振动的过程中会有位移，但通常相对弦的振动幅度属于微小位移，琴码可视为固定，可将其弦振动简化为有界弦的振动[17-18]。

设琴弦的有效弦长为L，以弦的左端固定点为原点，琴码端为终点，建立空间直角坐标系，弦长方向为x轴，垂直于弦长且平行于面板的方向为y轴，垂直于弦长且垂直于y轴的方向为z轴，弦的横向振动方向为u轴，弹拨点在x=x0处，简化模型如图1所示。

图1 古筝弦振动简化模型

古筝演奏中所用到的弹奏指法变化很多，其中最常用到的包括托、勾、抹、打等指法，这些演奏指法都是在弹拨琴弦的过程中给与弦初始状态后让其自由振动，但指法的不同也会致使弦的振动方向不同。以托、勾等指法为例，一般给与弦初始位移且施力方向为水平或向上，为此这里假设拨弦的方向为u轴方向，忽略拨弦“义甲”的宽度，则整个弦的初始位移在x轴方向成线性变化。设弹拨处弦的初始位移为u0，之后弦开始自由振动，则拨弦的振动可归结为定解问题[19]

(1)

式中：a2=T/ρ，T为弦张力；ρ为弦的线密度。

利用分离变量法，以傅里叶级数表达其定解为

(2)

其中

(3)

(4)

将式(3)、式(4)代入定解式(2)得

(5)

式(5)为拨弦的振动方程，其中n为正整数，n=1的部分为基波，其他每一个n代表一个谐波成分。

2 古筝弦-码结构的动力学建模分析

古筝演奏中弦-码的声学机理是利用义甲的弹拨使琴弦获得初始状态后自由振动，再通过琴码将琴弦的振动以力的形式传递到古筝面板。其传递过程主要是弦振动时琴弦的形态改变，使弦张力以及琴弦与码的夹角产生变化，使得通过琴码向下传递到面板的力不断改变，使古筝结构做强迫振动，从而发声[20-21]。

假设琴弦的有效振动弦长为L，琴码的作用高度为h，琴弦振动时弦张力为时变函数TL(t)，而琴弦给琴码向下的合力为时变函数F(t)，给琴码的侧向作用力为时变函数Fy(t)，弦振动的方向u轴垂直与弦长方向x轴，即在yz平面内，琴码两个码脚给面板的传递作用力分别为时变函数f1(t)、f2(t)，琴码在传递作用时的位移忽略不计，只考虑力的作用，琴码右边的按弦部分作用也忽略，可得到琴码传递的简化模型如图2所示。

图2 古筝琴码传递简化模型

从图2可知，进行受力分析琴弦张力为

(6)

式中：A=πd2/4，d为裸弦直径； Δl为弦振动时的形变量；E为弦芯钢丝的弹性模量；T为静态的弦张力。

根据拨弦时的弦振动方程式(5)分析弦的形变可知

(7)

其中

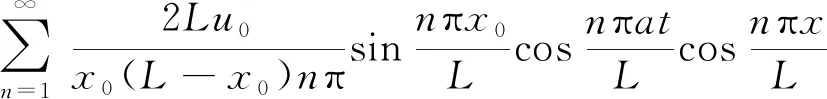
(8)

又由于u0相对于L为极小量，故

根据数学极限公式可得

(9)

将式(9)代入式(7)有

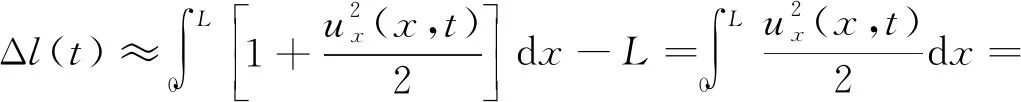
(10)

这里将弦的形变量表示为各阶弦振动形变的叠加项Δls(t)与相互间的耦合项Δlc(t)之和。

(11)

(12)

分析琴弦与琴码的位置关系和受力情况，得到其左半弦(振动部分)简化模型，如图3所示。图3中琴码的作用高度(即琴码端搁弦点相对岳山端搁弦点的垂直高度)为h，而琴码的实际高度为H，琴码的两码脚间距为b，弦长方向与面板的夹角为α，弦振动过程中TL(t)与x轴的夹角为时变函数β(t)，弦振动方向u轴与y轴的夹角为γ。

图3 古筝琴码传递简化模型

根据图3对弦-码结构的受力分析，可知，TL(t)可分解为x轴和u轴的分量，分别为

Tx(t)=TL(t)cosβ

(13)

Tu(t)=TL(t)sinβ

(14)

由式(13)和式(14)所示的TL(t)分力，可知琴码受到的作用力为

Fy(t)=Tu(t)cosγ

(15)

F(t)=Tx(t)sinα-Fz(t)cosα=Tx(t)sinα-Tu(t)sinγcosα

(16)

将琴码单独做受力分析，其正视图如图4所示。

根据图4的受力分析可知

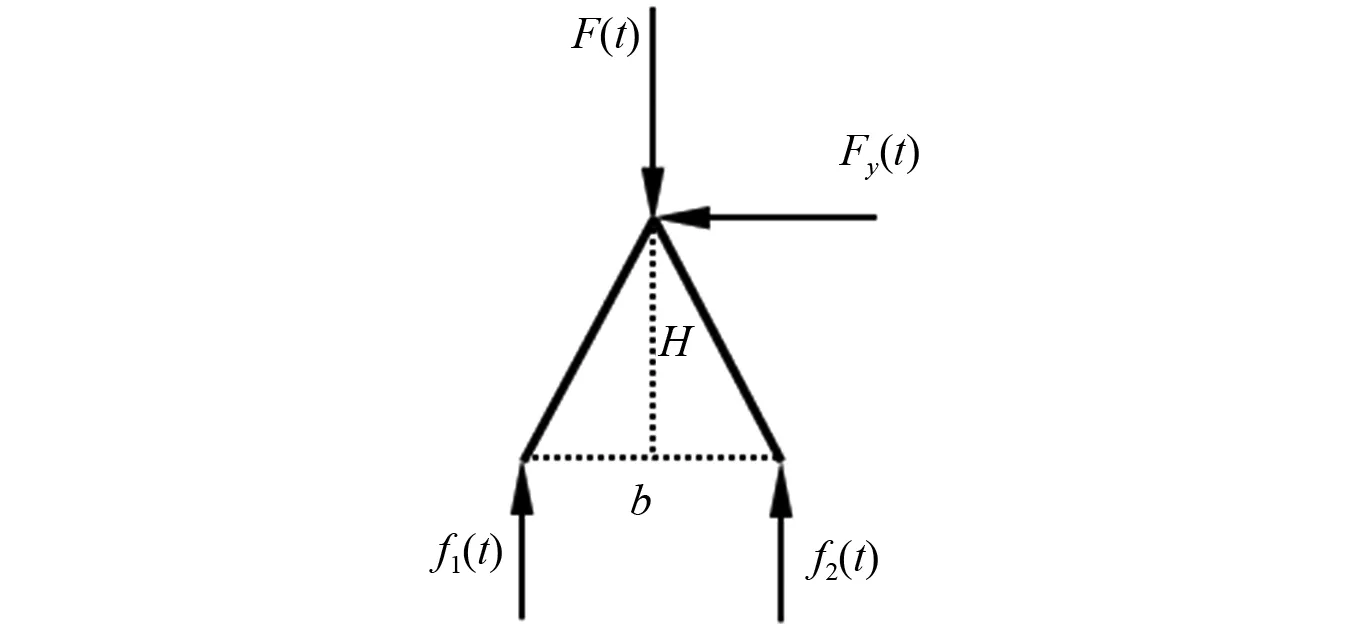
图4 琴码受力分析图

f1(t)+f2(t)=F(t)

(17)

f1(t)·b/2=f2(t)·b/2+Fy(t)·H

(18)

将式(17)和式(18)联立方程组求解可得

f1(t)=[F(t)+2Fy(t)H/b]/2

(19)

f2(t)=[F(t)-2Fy(t)H/b]/2

(20)

将式(13)～式(16)代入式(19)、式(20)可得

(21)

(22)

根据式(6)、式(8)、式(10)、式(11)、式(12)有

3 码脚作用力的数值分析与试验验证

根据理论推导的古筝两码脚作用力公式，通过MATLAB软件数值计算对其不同拨弦方式下码脚作用力的变化规律进行分析[22-23]，并通过试验测量进行对比验证。以古筝的21号弦为例，经过对上海民族乐器一厂生产的敦煌-698T传统古筝的测量，得到其琴弦的有效弦长L=950 mm，有效内径d=0.61 mm，线密度ρ=20.57 g/m，弹性模量E=220 GPa，阻尼系数ξ=0.35，利用Tensometric-Combi-490张力测量仪测得琴弦张力T=480 N，弹拨位置取常用演奏位置x0=1/7L处，最大初始位移u0=3 mm，而琴码的作用高度h=45 mm，琴码的实际高度为H=60 mm，琴码的两码脚间距为b=50 mm，弦振动方向u轴与y轴的夹角γ根据不同的拨弦方式，其分别取0°、45°、90°和135°。计算中取前10阶即n=10，计算时长t=1 s，时间间隔为Δt=0.000 04 s。

古筝琴码对面板作用力的测量。利用KD3001力传感器粘贴在处理过的琴码的左右码脚上，并保证其整体高度与原琴码一致，将传感器连AVANT-MI-2004调理放大器，信号通过9234采集卡连接至计算机，并利用LabVIEW进行试验测量，测试框图如图5所示。其中KD3001力传感器成圆环形，外径为φ16 mm内径为φ5 mm，且底面为平面，其测量范围在1～5 kN，自身固有频率在70 kHz，使用频率在20 kHz。

图5 琴码传递力测试框图

试验时，将弦的发音调至规定值，即21号弦所对应音名D的频率73.4 Hz，然后在弦1/7处沿y向(0°角方向)利用粘贴有应变片的模拟义甲进行拨弦，拨弦过程中实时监测应变片数值以确保拨弦初始位移的精确性和可重复性，同时记录弦振动时琴码左右码脚力变化的数据。将测量结果按照左、右码脚画出各码脚向下传递力试验结果曲线，并与MATLAB软件数值计算0°角的结果进行对比验证，同时根据时域曲线通过MATLAB软件对其进行快速傅里叶变换得到理论值和试验值的频谱曲线，如图6所示。各拨弦角度MATLAB软件数值计算结果左右码脚的作用力时域曲线如图7所示。

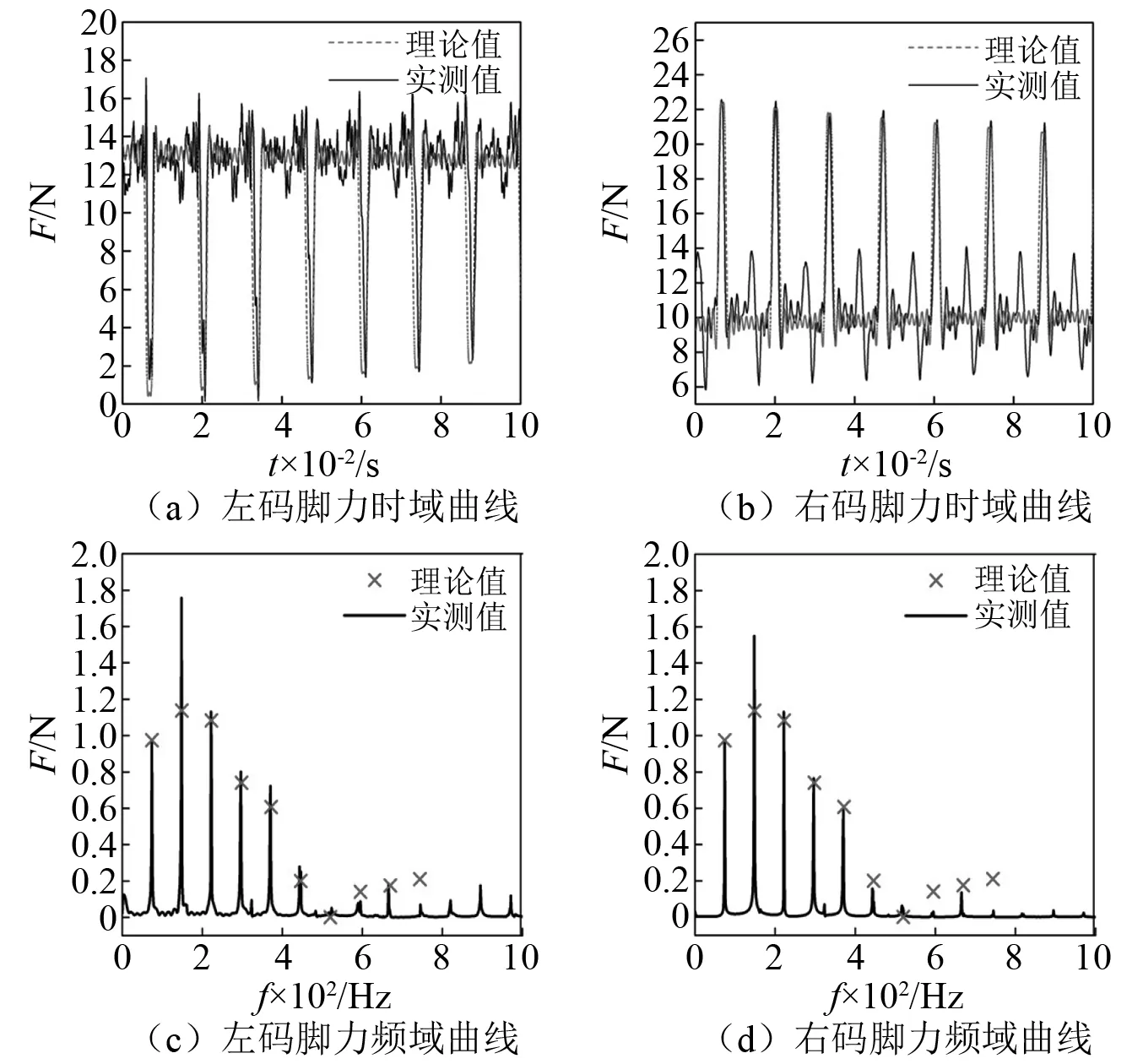
图6 0°角拨弦琴码向下传递力的理论值与试验值曲线对比

图7 各角度拨弦下左、右琴码向下传递力的时域曲线

图6描述的是0.1 s内琴码左右码脚作用力理论值与实测值曲线的对比，从图6可知，理论与实测曲线形状相似，其中时域曲线上左码脚理论值范围为0～15 N，而实测值为0～17 N，右码脚理论值范围为8.0～22.5 N，实测值为6.0～22.5 N，理论值与实测值基本相近，其主要的峰值出现的时间差也相近。频域曲线上左右码脚理论与实测结果的幅值变化趋势相似，其中理论值基本接近试验值，第2阶理论值小于试验值，相对误差较大，第7阶的理论值与实测值都接近为0。前4阶的具体数值对比和相对误差，如表1所示。

表1 琴码向下传递力理论值与试验值对比

总体来说琴码向下传递力的理论数值计算结果与实测值具有较好的一致性，考虑理论简化以及数值计算和试验测量的误差，可见理论计算的结果基本可信，弦-码结构三维动力学模型可行。其中频响结果中第2阶相对误差较大。原因与邓小伟的研究相同，忽略了面板与琴弦、琴码的耦合作用，因为在古筝结构振动试验中，古筝主结构的2阶固有频率为138.13 Hz[24]，与21号弦的2阶谐波频率146.8 Hz接近，可见其耦合作用较大，为此进一步工作中将着重解决其耦合效应。图7描述的是各拨弦角度琴码左右码脚作用力的时域曲线，结果显示：水平拨弦时(0°角)，左码脚动态力的最小值接近于0，说明该码脚几乎脱离琴体表面，可见水平拨弦易造成跳码，与实际古筝演奏情况符合；竖直拨弦时(90°角)，左右码脚的作用力同相位，且合力最大； 45°角拨弦与135°角拨弦琴码作用力正好左右反对称，且两种拨弦方式左右码脚的作用力相位相反。

4 结 论

通过简化古筝琴码为刚性双码脚，弦振动为有界弦振动，建立了弦-码结构的三维动力学模型，利用MATLAB软件数值计算分析了不同拨弦角度时各码脚法向作用力的变化规律，并进行了试验测量验证。对比发现左右码脚作用力的理论数值计算结果与实测值具有较好的一致性，考虑理论简化以及数值计算和试验测量的误差，可见理论计算的结果可信，弦-码结构三维动力学模型可行；水平拨弦时，左码脚动态力接近于0，可见水平拨弦易造成跳码；竖直拨弦时，左右码脚的作用力同相位，且合力最大； 45°角拨弦与135°角拨弦琴码作用力反对称，且两种拨弦方式左右码脚的作用力相位相反。