Event-Triggered Quasi-Synchronization of Fractional-Order Reaction-Diffusion Networks with Disturbance∗
2022-03-27YANGYapengHUChengYUJuan
YANG Yapeng,HU Cheng,YU Juan
(School of Mathematics and System Sciences,Xinjiang University,Urumqi Xinjiang 830017,China)
Abstract:This paper investigates the quasi-synchronization problem of fractional-order reaction-diffusion networks with bounded disturbance under event-triggered strategy.Firstly,in order to eliminate the influence of disturbances on the network,an event-triggered controller based on boundary layer method is proposed,and some sufficient conditions for achieving the quasi-synchronization are obtained.In addition,it is verified that Zeno phenomenon does not occur for each node based on the contradiction method.Finally,a numerical example is presented to verify the feasibility of the theoretical result.
Key words:fractional order;reaction-diffusion network;event trigger;disturbance
0 Introduction
Complex network is an abstract model for understanding the real world,which is composed of a large number of nodes and the interaction among nodes.Due to the great value in the field of engineering science,complex networks have received widespread attention in recent years.As an important research field of complex networks,synchronization implies that the dynamic states of all nodes are eventually identical by coupling among nodes or external control.Up to now,more and more excellent research results[1]on the synchronization of complex networks have been obtained.
Fractional calculus was proposed by Leibnitz in 1695.Because of its unique genetic characteristics and memory ability,fractional calculus can better simulate the dynamic behavior of real objects than the traditional integer-order calculus.Based on these advantages,the fractional calculus has been widely used in major areas,such as signal filtering,quantum mechanics,optical system and so on.Particularly,fractional-order models have been introduced into neural networks and multi-agent systems[2-3]by scholars and many excellent results have been obtained in recent years.
On the other hand,the dynamic behavior of most individuals is not only related to time,but also related to space.Therefore,the influence of spatial factors on the system state must be considered when establishing these mathematical models.In addition,the diffusion phenomenon of objects in production and life is inevitable,such as the process of heat conduction.In order to describe the real behavior of objects better,it is of practical significance to study complex networks with reaction-diffusion terms.Based on this,a large number of research results on reaction-diffusion complex networks[4]has been proposed.However,the synchronization of complex networks with both the fractional-order feature and reactiondiffusion terms is seldom noticed,which is one of the motivations of this paper.
Obviously,it is seriously difficult for complex networks to spontaneously achieve synchronization without any control in view of the individual difference of nodes.To achieve synchronization,various control strategies[5-6]have been proposed in recent years.All of the above controllers are not intelligent and may cause unnecessary waste.Fortunately,the eventtriggered control[7]is a good solution to this problem.In this mechanism,the controller updates its own state only when the state of the system satisfies the trigger condition,which greatly reduces the communication cost and a large amount of computing burden.
Inspired by the above analysis,the problem of quasi-synchronization is investigated for a class of fractional-order reaction-diffusion network with disturbance under an event-triggered strategy.Firstly,a general network model is considered,in which fractional-order feature,reaction-diffusion and disturbance are involved.Secondly,an event-triggered controller is designed by using the boundary layer technology to realize the quasi-synchronization.Thirdly,compared with the existing proof[8],an improved method is proposed to prove that the Zeno phenomenon will not occur under the proposed control strategy,which provides a new analytic method for fractional-order event-triggered control.
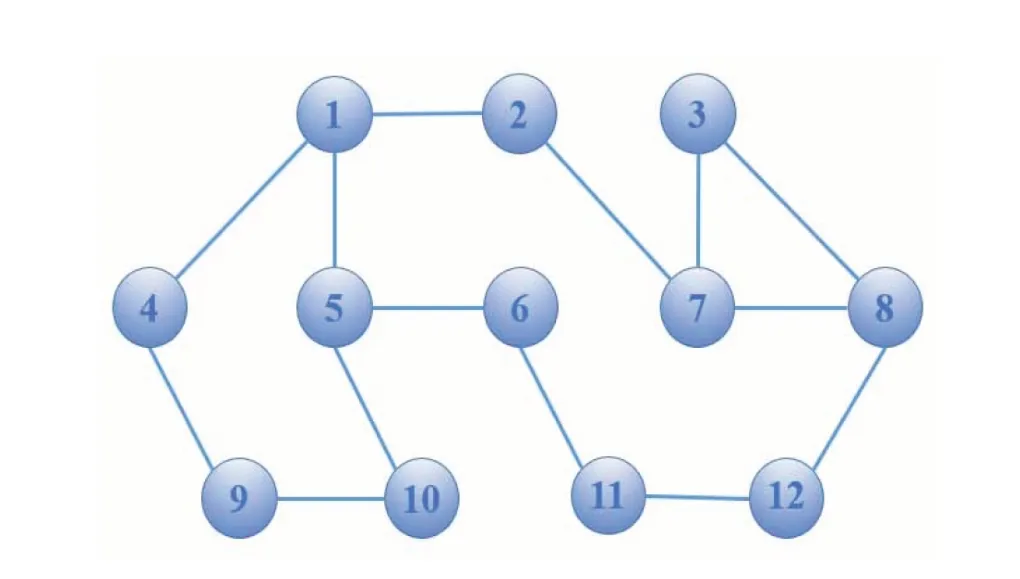
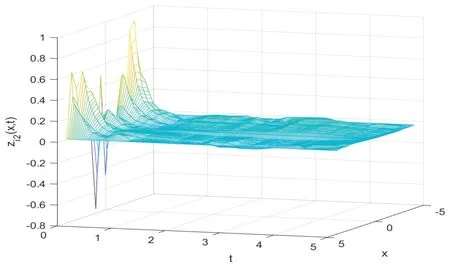
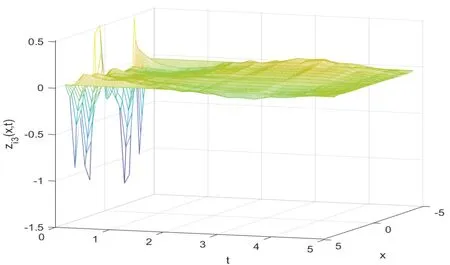
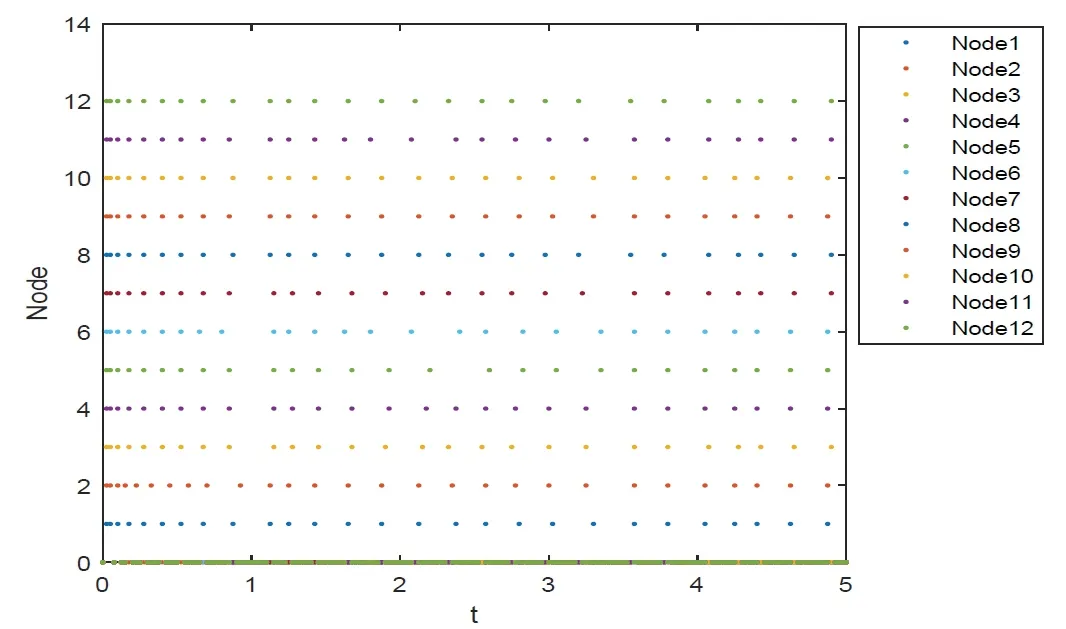
Notations:R stands for the set of real numbers and R+is the set of nonnegative real numbers.Rnis defined as ndimensional Euclidean space and Rm×nis the set of m×n real matrices.“T” represents the transpose of a matrix or vector.For a real symmetric matrix M ∈Rn×n,λMIN(M)and λMAX(M)denote the minimum and maximum eigenvalues respectively.M >0 (M ≥0) means that M is positive definite(semi-definite);M <0 (M ≤0) means that M is negative definite (semidefinite).⊗stands for the Kronecker product and Inis an n-dimensional identical matrix.Ω={x=(x1,x2,…,xκ)T∈Rκ:|xq| Definition 1[9-10]Let u(t):R+→R be an integrable function,the fractional-order integral of order α ∈(0,1)for u(t)is defined as Definition 2[9-10]Let v(t):R+→R be a differentiable function,the Caputo’s derivative of order α ∈(0,1) for v(t) is defined as Definition 3[11]For a function g(x,t):Rm×R+→R,which is differentiable in regard to t,the Caputo partial derivative on t is defined as Definition 4[9-10]For two scalars α>0 and β>0,the two-parameter Mittag-Leffler function is defined by where y ∈R.If β=1,the one-parameter form can be rewritten as Lemma 1[11]Suppose that w(x,t)∈Rnis a continuous differentiable vector function,α ∈(0,1),the following inequality holds Lemma 2[11]For a given continuous and square integrable function g(x):Ω →R,if g(x)satisfies g(x)|∂Ω=0,then Lemma 3[12]If V(t):R+→R+is a continuous differentiable function and satisfiesone has where 0<α<1,a>0 and b ≥0. Consider a fractional-order reaction-diffusion undirected network coupled by N nodes with disturbance,which can be described as follows where 0<α<1,yi=(yi1,yi2,…,yin)T∈Rnis the state vector of the ith node at time t with(x,t)∈Ω×R+,D=diag(d1,d2,…,dn)>0 is a diffusion matrix,A,B ∈Rn×nare both real matrices,f(yi)=(f1(yi1),f2(yi2),…,fn(yin)T∈Rnis the nonlinear function,c>0 is the coupling strength,H=(hij)N×Nis the coupling configuration matrix defined as follows:hij>0 if there is a link between node i and j,otherwise,hij=0 and the diagonal elements satisfy hii=is an external disturbance,ui(x,t)∈Rnis a control input to be designed,φi(x):Ω →Rnis the initial value. Assume that the target dynamic system is the following form where s ∈Rnis the state vector,φ(x):Ω →Rnis the initial value. Definition 5Network(1)is considered to be quasi-synchronized with the target system(3),if there exists a small error bound ∊>0 such that Denote the error vector zi(x,t)=yi(x,t)-s(x,t),one can easily obtain the following error system Assumption 1For each i=1,2,…,n,function fi(▪) satisfies the Lipschitz condition,that is,there exists a constant χi>0 such that Assumption 2The disturbance term ϖi(x,t) ∈Rnis bounded for each i=1,2,…,N,that is,there exists a constant wi>0 such that‖ϖi(x,t)‖≤wi. In this section,to investigate the quasi-synchronization between system(1)and system(2),an event-triggered controller is designed as follows Theorem 1Based on Assumptions 1 and Assumptions 2,network(1)achieves quasi-synchronization under the controller(4)and the trigger protocol(6)if ki>wiand Corollary 1If Assumption 1 and condition (7) are satisfied,then network (1) is asymptotically synchronized to the target system(2)with ϖi(x,t)=0 under the following controller and trigger condition: In order to avoid Zeno phenomenon,a positive minimum time interval must be guaranteed between two adjacent trigger instants. Theorem 2Under the conditions in Theorem 1,the Zeno phenomenon can be excluded,that is,there exists a minimum lower bound at any two trigger instants. ProofAccording to trigger condition(7),when twe have According to Theorem 1,synchronization error‖zi(x,tis)‖is ultimately uniformly bounded,which means that0.Therefore,Zeno phenomenon is avoided. In this section,a numerical example is given to verify the theoretical results. Consider the network topology shown in Fig 1.In system (1),choose N=12,x ∈Ω=[-4,4],α=0.9,yi∈R3,D=diag(0.04,0.04,0.04),A=diag(-1,-1,-1),fi(v)=0.5(|v+1|-|v-1|),i=1,2,3,link weights are given as follows:hij=1 if there is a link between node i and j,otherwise,hij=0,c=3.3,ϖi(x,t)= Fig 1 The topology of network(1) Fig 2 Synchronized error zi1(x,t) Under the above parameters,it is easy to obtain that function f(yi(x,t))satisfies the Lipschitz condition with the Lipschitz constant χ=1 and ‖ϖi(x,t)‖≤wi=0.616.In controller (4) and trigger condition (6),select parameters η1=0.4,η2=0.2,η3=0.4,ki=5,ςi=0.1.Obviously,for i=1,…,12,ki>wi.By simple calculation,λMAX(Π)=-2.547 4<0,which satisfies condition(7)in Theorem 1.Eventually,the synchronization error zi(x,t)converges to the set ℜ={z(x,t):‖z(x,t)‖2≤1.72}.The synchronized errors are displayed in Fig 2~Fig 4.Fig 5 shows the event-triggered instants of each node,which shows that Zeno phenomenon is excluded. Fig 3 Synchronized error zi2(x,t) Fig 4 Synchronized error zi3(x,t) Fig 5 Event-triggered instants In this paper,the quasi-synchronization of fractionalorder reaction-diffusion networks with bounded disturbance under event-triggered strategy has been considered.By using the boundary layer method,a novel event-triggered controller has been designed and an effective trigger condition has been proposed.Based on the proposed control strategy,some conditions for quasi-synchronization of addressed network have been obtained and Zeno phenomenon is eliminated by means of theoretical analysis.Future work will consider the synchronization problem of fractional-order reaction-diffusion networks under the event-triggered impulsive control.1 Preliminaries and Model Description
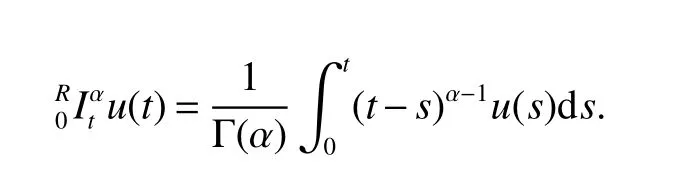
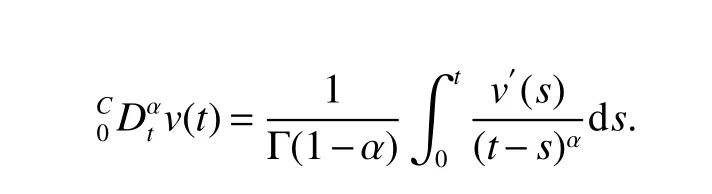
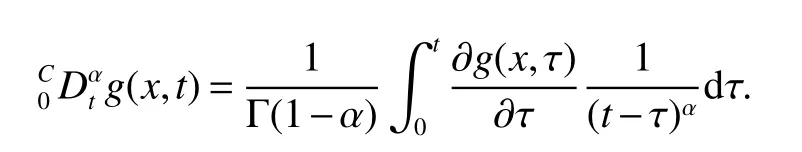
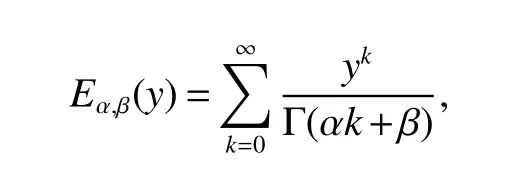
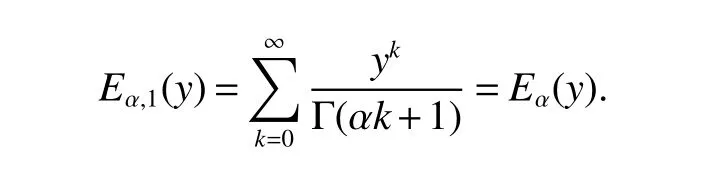
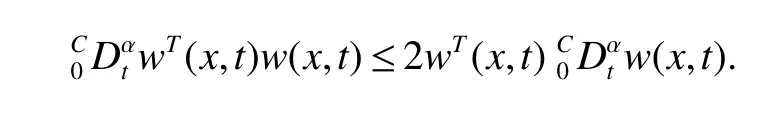
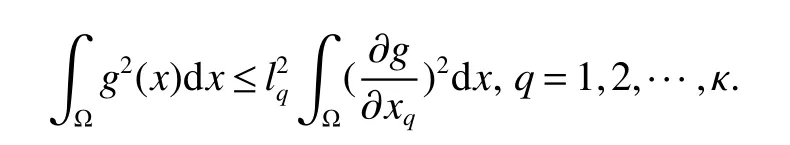
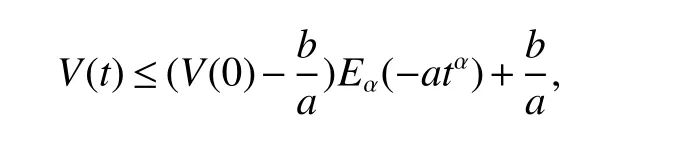
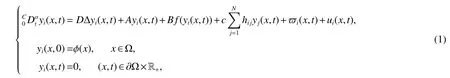
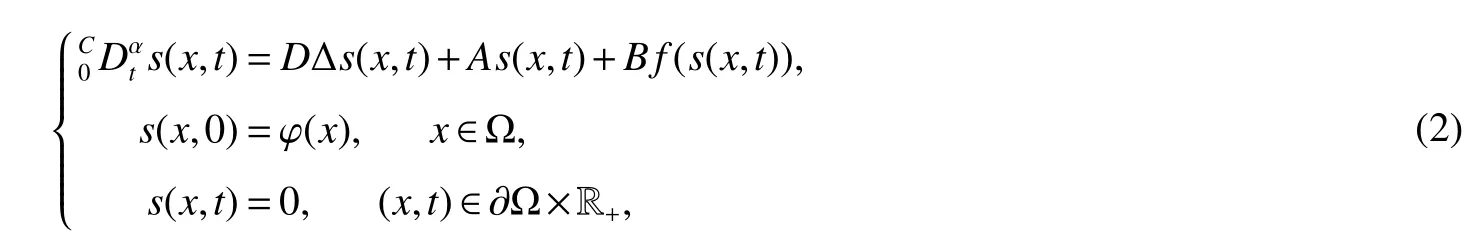
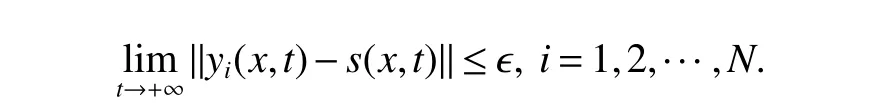
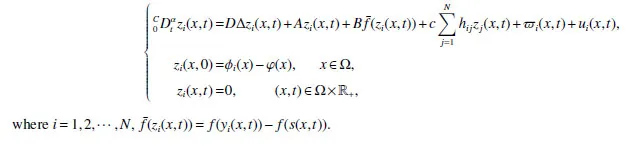
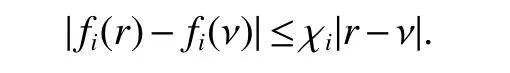
2 Main Results






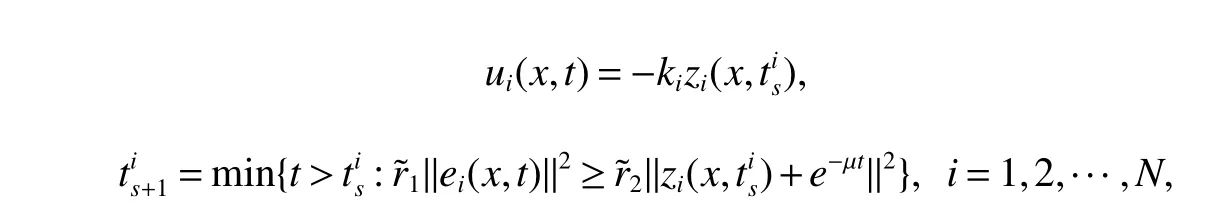


3 Numerical Simulations
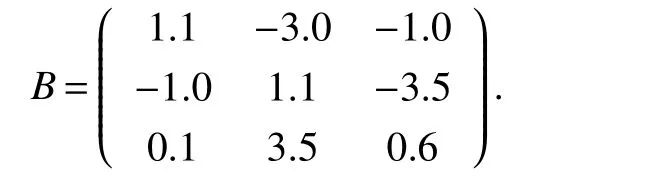

4 Conclusion
