具有脉冲效应和随机扰动的Markov 跳跃主从多智能体系统固定时间一致∗
2022-03-27夏孟瑶蒋海军于志永
夏孟瑶,蒋海军,于志永
(新疆大学 数学与系统科学学院,新疆 乌鲁木齐 830017)
0 引言
近几十年来,多智能体系统的协同控制因其在无人机、航天器姿态协调、电网电源管理[1-3]等领域的广泛应用而引起了人们的广泛关注.一致性行为是一种合作控制行为,其目的是使智能体之间通过信息交换从而达成某种统一的协议.到目前为止,为了解决多智能体系统一致性问题,学者们从不同的方面提出了不同的有效的控制协议,如事件触发控制、滑模控制等[4-5].
在实际环境中,像物理系统、机械设备系统等网络系统往往会受到不确定性环境的影响,这种干扰可以称为随机干扰.文献[6]为了处理未知和时变问题提出了时变一致性方案,解决了一类不确定随机非线性多智能体系统的时变一致性问题.在另一个学术领域,Markov 跳跃系统受到了广泛的关注,因为它是一种混合系统,具有描述大多数物理系统结构突变的优势,如意外事件和不受控制的结构型变化.它是在不同时间从一种模式切换到另一种模式的切换系统,不同模式之间的切换可以通过Markov 链来实现.文献[7]研究了一类具有Markov 特征的二阶多智能体系统的一致性问题,其中随机切换拓扑和随机通信时滞由两个相互独立的Markov 链所控制.直到现在,研究Markov 跳跃的随机多智能体系统较少.因此,本文考虑了具有Markov 跳跃的随机主从多智能体系统.
在动力系统的演化过程中,由于受外部环境干扰或者机器发生故障,系统在某一时刻发生的突然变化称为脉冲效应[8-10].脉冲效应作为一种普遍存在的现象,有很多优点和缺点,它的优点是提高数据安全性,降低控制成本.缺点是它会破坏系统的性能.文献[10]设计了一种混合有限时间稳定控制器,利用Lyapunov 函数给出了脉冲动力系统的有限时间稳定条件.
与现有的研究相比,本文的主要贡献如下:(1) 本文考虑了具有脉冲效应的Markov 跳跃和随机扰动的主从多智能体系统;(2) Markov 跳跃函数不仅存在于系统中,而且应用于所设计的控制器中.同时,本文还考虑了脉冲效应.从而使得系统在固定时间内达到一致.
1 模型建立及预备知识
首先,给出本文所用到的记号.其中Rn表示n 维欧几里得空间.‖·‖ 表示欧几里得范数.IN表示N 维单位矩阵.对于矩阵 A,AT,λmax(A) 和λmin(A) 分别代表矩阵A 的转置、最大特征值和最小特征值.A>0 表示矩阵A 是一个正定矩阵.diag(·) 表示对角矩阵.sign(·) 代表符号函数.E{·} 表示数学期望.
考虑由N 个智能体所组成的网络,网络拓扑图由图G=(V,E) 表示,其中V={1,2,···,N} 表示节点集,E={(i,j)|i,j ∈V} 表示边集,记智能体i 的邻居节点集为Ni={j|(i,j)∈E}.A=[aij]∈RN×N是图G 的邻接矩阵,若(i,j)∈E,则aij>0,否则,aij=0.对于无向图G 来说,aij=aji.记节点的度矩阵为D=diag{d1,d2,···,dN},其中P 则图G 的拉普拉斯矩阵定义为L=D-A.令矩阵H=L+B,其中B=diag{b1,b2,···,bN},如果智能体i 能够接收到领导者的信息,则bi=1,否则,bi=0.
Markov 链r(t)(t ≥0) 在概率空间(Ω,F,Ft≥0,P) 上是右连续的,它在有限集S={1,2,···,s} 上取值且算子θ=[θdρ]s×s(d,ρ ∈S) 满足

第i 个跟随者智能体的随机动力系统描述为

其中r(t),t ≥0 表示在t 时刻马尔可夫过程的模态演变过程.A(r(t)),B(r(t))∈Rn×n表示模态为r(t)的常数矩阵.xi(t)∈Rn,(i=1,···,N) 表示第i 个智能体的状态,ui(r(t))∈Rn代表第i 个智能体的控制输入向量.f(·)∈Rn表示i 个智能体的连续函数.g(·)∈Rn×n为跟随者智能体的噪声强度函数.w(t)∈Rn表示布朗运动,并且满足E{dw(t)}=0 和E{[dw(t)]2}=dt,假设Markov 链r(·) 与布朗运动w(·) 是相互独立的.

领导者x0(t) 的随机动力系统描述为其中x0(t)∈Rn表示领导者的状态,f(x0(t),t)∈Rn表示领导者的连续函数,g(x0(t),t)∈Rn×n表示领导者的噪声强度函数.
下面给出一些假设、引理和定义.
假设1对于任意的向量x ∈Rn,y ∈Rn,假设函数f(·) 是Lipschitz 连续的,则存在一个常数k1>0 使得
‖f(x(t),t)-f(y(t),t)‖≤k1‖x(t)-y(t)‖.
假设2对于噪声强度函数g(xi(t),t),xi(t)∈Rn满足以下Lipschitz 条件

定义1对于一个时间T(0) 不依赖于系统初值xi(0),x0(0),如果说系统(2) 和系统(3) 在固定时间内达到一致,则有limt→TE{‖xi(t)-x0(t)‖}=0 和E{‖xi(t)-x0(t)‖}≡0,t ≥T 成立.其中T 为停息时间.
2 主要结论
为了实现固定时间一致,设计以下切换反馈控制器



则根据引理2 得到停息时间T 为
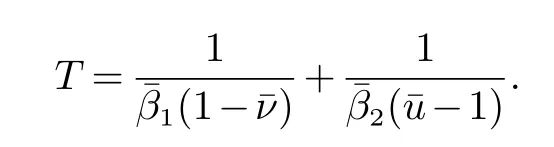
根据以上分析,存在一个与智能体的初值状态无关的时间T,使得
根据定义1 可得随机多智能体系统(2) 和(3) 在控制协议(4) 下能够在固定时间内达到一致.
当系统不带有随机干扰时,则可以将系统(2) 和(3) 改写为以下模型

注1推论1 的证明与定理1 的证明相同,但是α1(r(t))的取值范围不同.因为系统(2)和(3)中存在随机干扰,所以定理1 中的α1(r(t)) 取值与k2有关.而推论1 中的α1(r(t)) 取值与k2无关,所以在随机系统(1)和(2)中α1(r(t)) 的取值范围比系统(14)和(15) 中的更为严格.
3 数值模拟
在本节将以数值模拟来验证本文所提出的控制算法的正确性.
考虑具有Markov 跳跃的主从随机多智能体系统,令n=2,N=5,并选取如下的转移概率矩阵P

脉冲增益矩阵选取为
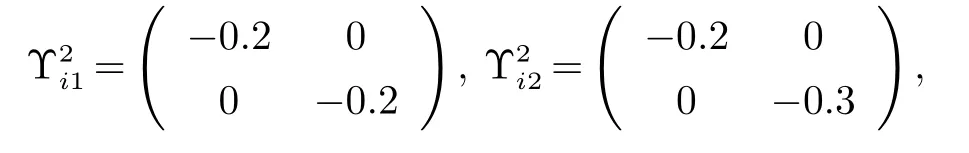
非线性函数fi(xi(t),t) 选取为
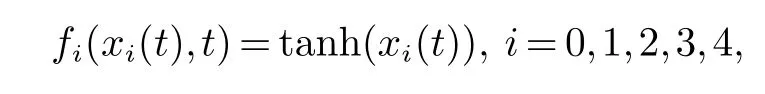
噪声强度函数g(xi(t),t) 为

令智能体的初值状态为x0=(-30,12)T,x1=(25,-20)T,x2=(14,-23)T,x3=(-10,-5)T,x4=(-40,-6)T.
图1 表示系统维纳过程.图2 表示定理1 中的Markov 切换过程.图3 和图4 描述了在系统不受控制的条件下智能体的状态轨迹图.

图1 维纳过程
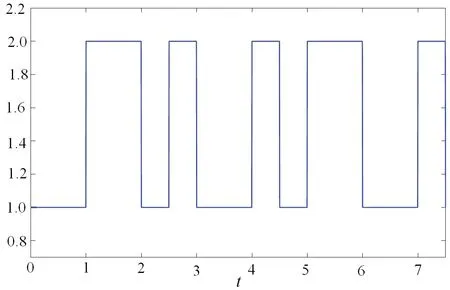
图2 Markov 切换过程
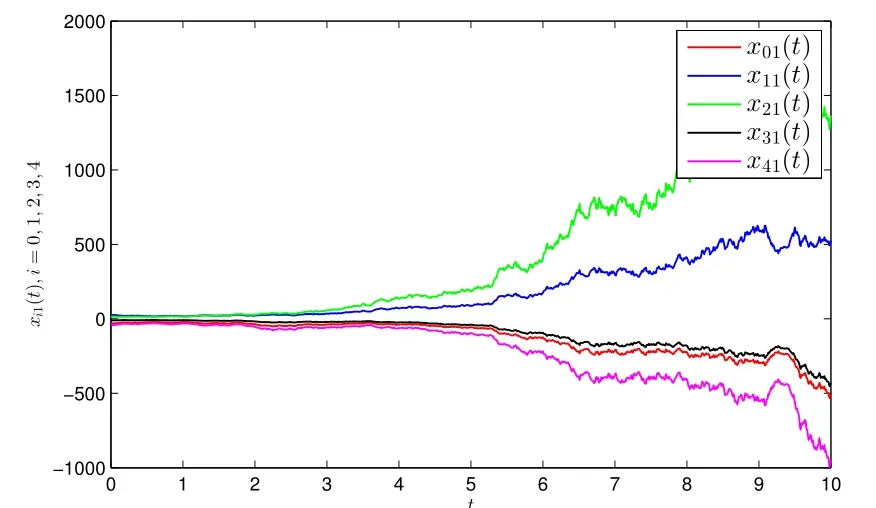
图3 无控制下的智能体xi1(t) 状态轨迹

图4 无控制下的智能体xi2(t) 状态轨迹
通过选取满足假设定理的合适参数k1=1,k2=2,α1(1)=0.73,α1(2)=0.69,β1(1)=0.9,β1(2)=1.15,β2(1)=1.2,β2(2)=0.8,qd=1.02,并令ν=0.4,u=1.2,得到了固定时间一致的图,其中图5 和图6 表示控制下的智能体的状态轨迹.从数值模拟中可以看到本文所设计的控制器的有效性.
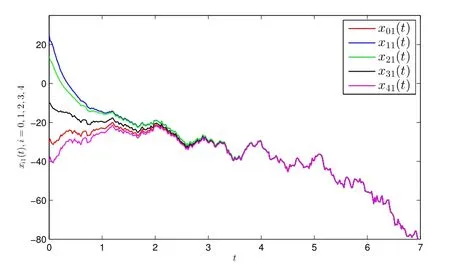
图5 控制下的智能体xi1(t) 状态轨迹

图6 控制下的智能体xi2(t) 状态轨迹
4 结论
本文考虑了具有Markov 跳跃的主从随机多智能体系统的固定时间一致性问题.考虑综合因素,设计了具有脉冲效应的非线性状态反馈切换控制协议.通过应用线性矩阵不等式、随机分析理论以及Lyapunov 稳定性理论给出了主从多智能体系统在固定时间内达到一致的相关准则.
