基于非周期间歇控制的复值惯性神经网络指数同步∗

惠姣姣，于娟

(新疆大学 数学与系统科学学院，新疆 乌鲁木齐 830017)

0 引言

1986年,Babcock 和Westervelt[1]将电感引入到神经电路来模拟惯性特性,这种用二阶微分方程描述的神经网络被称为惯性神经网络.惯性神经网络不仅比传统的一阶神经网络模型具有更复杂的动力学特性,还具有广泛的生物学背景[2-3].因此，惯性神经网络的动力学和同步性研究受到了更多学者的广泛关注.

目前,研究惯性神经网络动力学的方法主要包括变量转换法、矩阵测度法和非降阶法.其中非降阶法因其能够有效地降低理论推导难度并能保留系统的惯性特征而被广泛应用于惯性神经网络的稳定性、正定性、周期性和同步性等研究中.然而,目前基于非降阶法的研究工作[4-6]主要集中于探讨实变量的惯性神经网络模型,而关于更一般的复值惯性神经网络的相关研究结果较少.事实上,复值惯性神经网络可以用于更广泛的领域,包括图像重建、非线性滤波和模式的识别与分类.另外,在当前的复值神经网络[7-9]研究中,实虚部分离法是一种常用的理论分析技巧,其主要思想是先将复值惯性神经网络模型分解成两个实值子系统,再对子系统进行讨论.虽然这种分离方法是有效的,但会增加理论分析的难度.文献[10]在不分离复变量的前提下,分析了复值忆阻神经网络固定时间同步问题.目前,在不分离复变量的框架下,通过非降阶法分析复值惯性神经网络同步控制问题仍具有挑战性.

相比于连续反馈控制,间歇控制作为一种不连续的控制策略,能够更有效地节约控制成本,近年来被广泛应用到各种神经网络[11-13]的研究中.但是,很少有学者讨论在非周期间歇控制下的复值惯性神经网络的指数同步问题.

基于上述讨论,本文将基于非周期间歇控制探讨具有变时滞的复值惯性神经网络指数同步问题,主要结论包含以下几个方面.第一,建立了具有离散时滞和分布时滞的复值惯性神经网络模型,它比传统的惯性神经网络[14]更具有一般性；第二,直接对复值响应神经网络设计间歇控制策略,不仅避免了现有研究[15-16]中将惯性神经系统先降次再控制的复杂控制设计,还降低了将复值系统划分为两个实值子系统引起的理论推导难度；第三，通过直接对同步误差系统构造Lyapunov 泛函,得到了具有较低保守性的指数同步判据.

1 模型的描述及预备知识

考虑如下复值惯性神经网络模型:

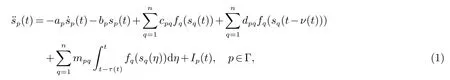
其中:sp(t)表示第p 个神经元在t 时刻的状态向量,二阶导数表示系统(1)的惯性项,ap>0,bp>0,cpq,dpq和mpq代表复值的连接权重,fq(·)是第q 个神经元的复值激活函数,ν(t)和τ(t)是时变时滞且满足0<ν(t)≤ν,˙ν(t)≤ν*<1,0<τ(t)≤τ 以及˙τ(t)≤τ*<1,Ip(t)是外部输入.

系统(1)的初始条件为

其中:p ∈Γ,ℑ=max{ν,τ},φp(χ)和ψp(χ)是连续有界函数.

设系统(1)为驱动系统,对应的响应系统为

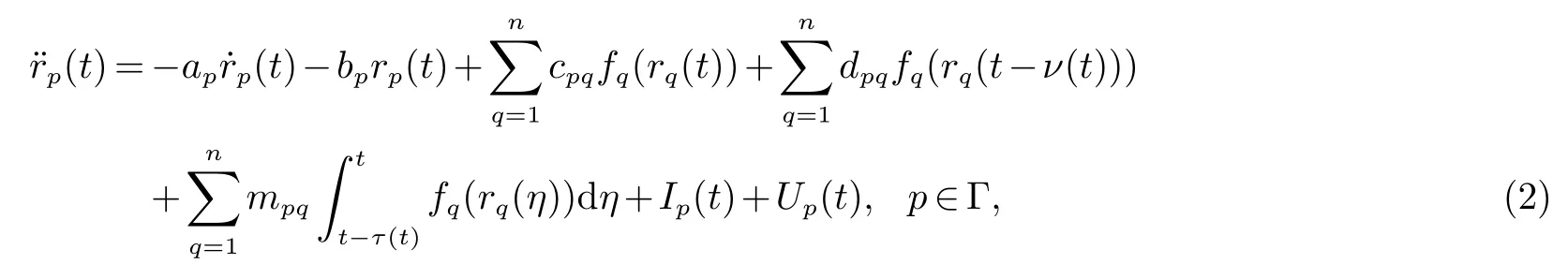
其中:rp(t)为响应系统中第p 个神经元的状态,Up(t) 是间歇控制器,其他符号的定义与系统(1)中的相同.

系统(2)的初始条件为

其中:p ∈Γ,k ∈N+,εp>0 和δp>0 表示控制增益,tk和σk分别表示第k 个间歇周期内的控制开始时间和停息开始时间.

2 主要结论

定义wp(t)=rp(t)-sp(t)是同步误差,由系统(1),系统(2)和控制器(3)可得误差系统:

定理1在假设1～3 下, 若存在两个正数和µ使得则系统(1)和(2)在控制器(3)下达到指数同步.

证明构造如下的Lyapunov 泛函

由定义1 可知,系统(1)和系统(2)是指数同步的.

定义Θ={p ∈Γ:Ap=0}.根据假设3 易知,对任意的p ∈Γ,有Cp=0 和Bp≤0.显然,当tk≤t ≤σk时,V˙(t)≤0.当αp=βp(ap+bp+εp+δp-2µ-1) 时,即Cp=0,假设3 可以改为如下的假设.

假设4存在正常数βp使得

推论基于假设1,2,4,如果Ξ=µ-Π>0,则系统(1)和系统(2)在控制器(3)下是指数同步的.

注1在文献[4]中,非降阶法被用来讨论具有离散时滞的实值惯性神经网络指数稳定问题.相比于此工作,本文提出了一类更一般的模型,即具有混合时滞的复值惯性神经网络模型,并得到了保证驱动-响应系统指数同步的新准则.

3 数值模拟

考虑如下复值惯性神经网络模型:

驱动系统(14) 的动力学行为如图1 和图2 所示.其中:初值为φ1(χ)=0.2-0.3i,ψ1(χ)=-0.5+0.3i,φ2(χ)=-0.6+0.2i,ψ2(χ)=0.4-0.7i,χ ∈[-1,0].

图1 系统(14)的实值部分的混沌行为

图2 系统(14)的复值部分的混沌行为

选取控制增益为ε1=5,ε2=8,δ1=19,δ2=24,非周期间歇控制的控制时间序列为:[0,1],[2,3.2],[4,7.2],[8,9.4],[12.7,15.8],[16,19],[20.1,23],[23.9,25.3],[27,30],[30.5,32.5],[34,35.5],[37,39.5],[40,43.5],[45,47.8],[50,55],···.

显然,L1=L2=1,0<ν(t)<ν<1,0<ν˙(t)<ν*=0.25,τ(t)=τ=1,τ˙(t)=τ*=0.选取µ=0.1,α1=47.5,α2=32.7,β1=2,β2=1.则A1=-0.881 83,A2=-0.209 58,B1=-0.125 97,B2=-0.355 40,C1=-0.3,C2=-0.1.由定理1 可知驱动系统(14)和响应系统(15)是指数同步的,模拟结果见图3～图7,图8 为间歇控制策略的时间演化.

图3 s1 和r1 实值部分的同步图

图4 s1 和r1 复值部分的同步图

图5 s2 和r2 实值部分的同步图

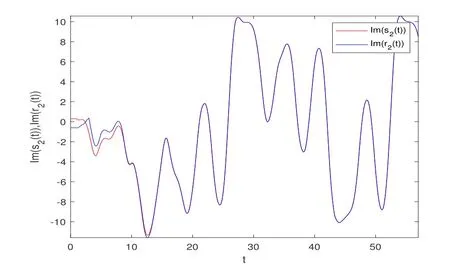
图6 s2 和r2 复值部分的同步图

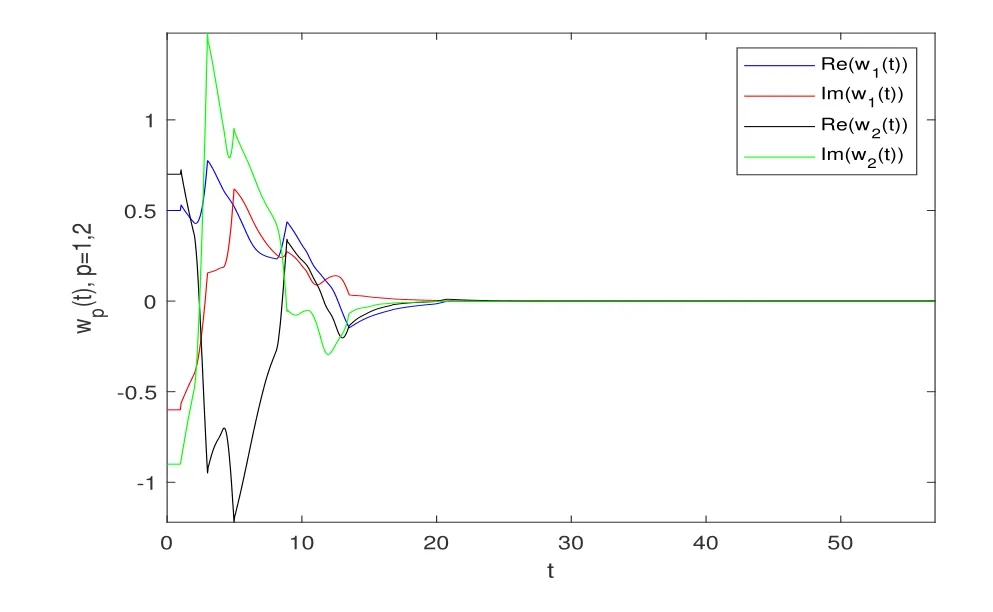
图7 同步误差模拟

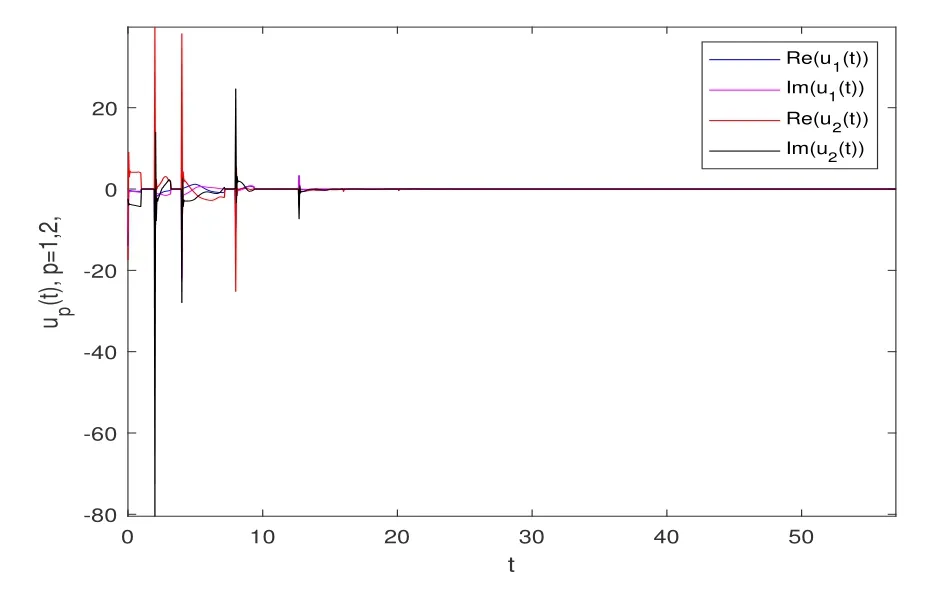
图8 控制器的时间演化

4 结束语

与一阶神经网络相比,惯性神经网络拥有较快的收敛速度,较强的近似估计能力以及较大的存储能力和容错能力.并且,深入地探讨惯性神经网络的动力学和同步控制问题,有助于惯性神经网络模型对自动化控制、医学、语音识别、海洋遥感、图像处理以及信息科学等领域提供宏观指导.因此,研究惯性神经网络具有很重要的实际意义和应用价值.本文的主要创新包括:

(1)不同于大部分文章使用的复变量分离法,本文直接在复数域上构造复值的Lyapunov 泛函并设计复值间歇控制器,直接分析惯性神经网络模型的动力学行为,并给出了具有混合时滞的复值惯性神经网络同步判据.

(2)本文采用的非降阶法在最大程度上保留了惯性项的惯性特征,降低了理论推导难度并且所得的结果具有较低的保守性.