2021年高考试题模型建构能力命题评价设计与分析

高翔

摘 要：高考试题强化核心知识多个维度的考察，注重知识单元内的综合和跨知识单元的综合.问题情境紧贴时代发展的脉搏，注重科技和生产中的物理知识的运用，从学生熟悉的物理情境中进行命题，强化基本概念的理解和规律的应用.

关键词：科学思维;模型建构;能力层阶;学习水平;心智模式

中图分类号：G632   文献标识码：A   文章编号：1008-0333（2022）04-0101-08

2021年全国高考试卷和部分省市的试题比较好地体现了物理学科素养层阶评价的命题指导思想，其中全国甲卷和乙卷最为优秀，这两张试卷比较好地体现了以高考评价体系为依托，突出核心知识、重点知识和基础性知识的考察.

高考试题强化核心知识多个维度的考察，注重知识单元内的综合和跨知识单元的综合.问题情境紧贴时代发展的脉搏，注重科技和生产中的物理知识的运用，从学生熟悉的物理情境中进行命题，强化基本概念的理解和规律的应用.比较合理地从素养要求的层阶出发，注重物理观念、科学思维、科学探究和科学态度与责任素养层次的考察.在推进课程实践的深化期，这一命题方式比较好地引导中学物理教学的发展.为发挥高考命题的指导功能，我们从模型建构的能力层阶的视角选择山东卷和全国卷的典型问题进行解读.

1 “识别—运用—创造性应用”能力层阶的命题设计

依据运用模型解决问题的层级，从学习能力上分为：在熟悉的问题情境中再认、在相似的问题情境中识别和通过类比与联想等方式形成相似的意向三种层次.

层阶一：在熟悉的问题情境中“识别—运用—创造性应用”的命题设计

典例1 （山东省2021年普通高中学业水平等级考试物理）

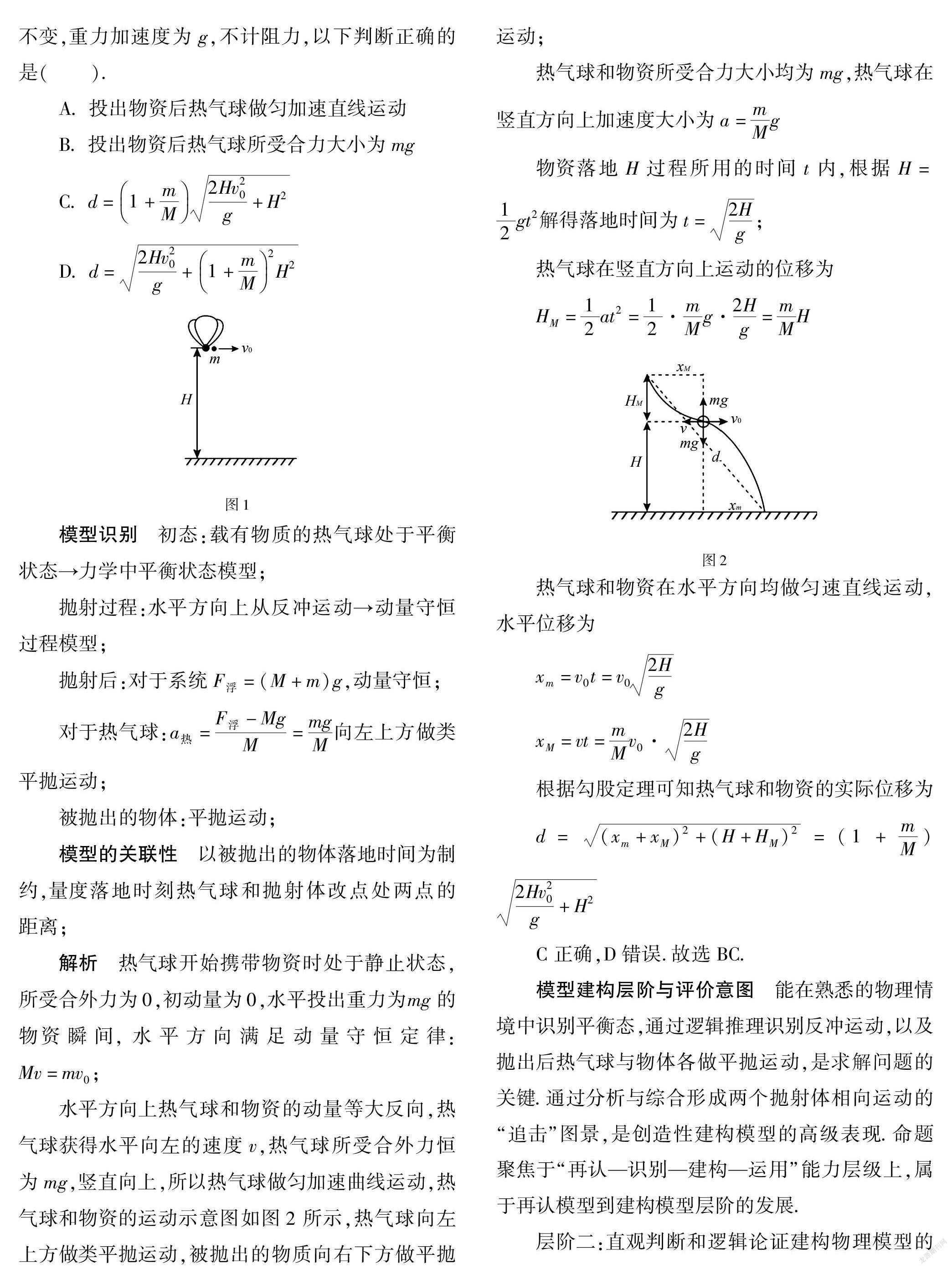
11.如图1所示，载有物资的热气球静止于距水平地面H的高处，现将质量为m的物资以相对地面的速度v0水平投出，落地时物资与热气球的距离为d.已知投出物资后热气球的总质量为M，所受浮力不变，重力加速度為g，不计阻力，以下判断正确的是（  ）.

A. 投出物资后热气球做匀加速直线运动

B. 投出物资后热气球所受合力大小为mg

C. d=1+mM2Hv20g+H2

D. d=2Hv20g+1+mM2H2

图1

模型识别 初态：载有物质的热气球处于平衡状态→力学中平衡状态模型;

抛射过程：水平方向上从反冲运动→动量守恒过程模型;

抛射后：对于系统F浮=（M+m）g，动量守恒;

对于热气球：a热=F浮-MgM=mgM向左上方做类平抛运动;

被抛出的物体：平抛运动;

模型的关联性 以被抛出的物体落地时间为制约，量度落地时刻热气球和抛射体改点处两点的

距离;

解析 热气球开始携带物资时处于静止状态，所受合外力为0，初动量为0，水平投出重力为mg的物资瞬间，水平方向满足动量守恒定律：Mv=mv0;

水平方向上热气球和物资的动量等大反向，热气球获得水平向左的速度v，热气球所受合外力恒为mg，竖直向上，所以热气球做匀加速曲线运动，热气球和物资的运动示意图如图2所示，热气球向左上方做类平抛运动，被抛出的物质向右下方做平抛运动;

热气球和物资所受合力大小均为mg，热气球在竖直方向上加速度大小为a=mMg

物资落地H过程所用的时间t内，根据H=12gt2解得落地时间为t=2Hg;

热气球在竖直方向上运动的位移为

HM=12at2=12·mMg·2Hg=mMH

图2

热气球和物资在水平方向均做匀速直线运动，水平位移为

xm=v0t=v02Hg

xM=vt=mMv0·2Hg

根据勾股定理可知热气球和物资的实际位移为

d=（xm+xM）2+（H+HM）2=（1+mM）2Hv20g+H2

C正确，D错误.故选BC.

模型建构层阶与评价意图 能在熟悉的物理情境中识别平衡态，通过逻辑推理识别反冲运动，以及抛出后热气球与物体各做平抛运动，是求解问题的关键.通过分析与综合形成两个抛射体相向运动的“追击”图景，是创造性建构模型的高级表现.命题聚焦于“再认—识别—建构—运用”能力层级上，属于再认模型到建构模型层阶的发展.

层阶二：直观判断和逻辑论证建构物理模型的命题设计

在新的物理情境中移用或借用熟悉的物理模型解决物理问题的方式，经历“选择模型—模型验证—模型分析—创造性应用”的逻辑论证过程，它是模型建构的低转换形态.

典例2 （山东省2021年普通高中学业水平等级考试物理）

8.迷你系绳卫星在地球赤道正上方的电离层中，沿圆形轨道绕地飞行.系绳卫星由两子卫星组成，它们之间的导体绳沿地球半径方向，如图3所示.在电池和感应电动势的共同作用下，导体绳中形成指向地心的电流，等效总电阻为r.导体绳所受的安培力克服大小为f的环境阻力，可使卫星保持在原轨道上.已知卫星离地平均高度为H，导体绳长为LLH，地球半径为R，质量为M，轨道处磁感应强度大小为B，方向垂直于赤道平面.忽略地球自转的影响.据此可得，电池电动势为（  ）

图3

A. BLGMR+H+frBL

B. BLGMR+H-frBL

C. BLGMR+H+BLfr

D. BLGMR+H-BLfr

模型建构能力的表现

1.解读物理情境识别模型的能力

（1）表象复原与物理情境的解读-地磁分布的特征与赤道上方地磁场与地面平行物理情境的复原;

（2）等效模型的建构-卫星离地平均高度为H，导体绳长L（LH），说明两卫星近似具有相等的线速度，建构F万=Fn，形成GMm（R+H）2=mv2R+H，建构匀速圆周运动模型，从而形成v=GMR+H的认识;

2.逻辑推理建构物理模型的能力

在新的物理情境中直观判断并进行识别和通过分析与推理进行“迁移”性应用是建构模型的两种形式.通过逻辑推理形成因果判断，从必然性的角度分析论证事物存在的关系，形成与事实一致的判断.通过逻辑论证建构模型的层阶如下：

（1）直观判断

①题干给出导线运动方向，需要借助地球磁场分布的图景判断感应电流的流向自下而上，与电池提供的电流方向相反.这种借助图示判断的要求较高，但不是判断感应电流流向的唯一方法;

②导体棒平动切割磁感线产生动生电动势，在闭合回路中产生感应电流.与谁组合成闭合回路？从题干给出的图景信息知，近地与远地卫星与所处的电离层构成闭合回路;

（2）逻辑判断

①导体棒在磁場中平动切割磁感线产生动生电动势，要受到电磁阻尼的作用，而题干给出“在电池和感应电动势的共同作用下，导体绳中形成背向地心的电流”，则闭合回路中的电流I=E-E感r=E-BLGMR+Hr;

②导体绳所受的安培力克服大小为f的环境阻力，可使卫星保持在原轨道上运行，则：F安=f，即f=BE-E′rL，解得E=BLGMR+H+frBL;

将复杂的物理情境分解为“闭合电路的识别”、“电磁感应中电磁阻尼与电磁驱动”、“力学平衡”和“匀速圆周运动”模型，通过直观判断各物理模型成立的条件，经逻辑推理借助于经验，选择适合的物理模型，通过尝试性解答验证选择模型的合理性，从题干给出的要求与解答结果的匹配性上证实模型建构的科学性，这是逻辑推理建构物理模型的方式，属于较高层阶的转换.

解析 根据GMm（R+H）2=mv2（R+H），可得卫星做圆周运动的线速度v=GMR+H

根据右手定则知，导体绳产生的感应电动势上端为正极的电源，大小为E′=BLv;

导线绳所受阻力f与安培力F平衡，则安培力与速度方向相同，可知导线绳中的电流方向向下，即电池电动势大于导线绳切割磁感线产生的电动势 ，可得f=BE-E′rL ;

解得E=BLGMR+H+frBL ，故选A.

2 “选择—转换—建构”能力层阶的命题设计与要素分析

将复杂的问题情境分解成若干个递进发生的物理事件，分析每一个物理事件的初始状态和变化的过程，厘定各物理事件的外控因素，从熟悉的物理情境中尝试使用熟悉的物理模型解决问题，或者通过移用、类比和联想的方式，基于经验的判断选择某一个物理模型解决问题.

层阶三：逻辑推理证实，类比转化为建构的物理模型

将一个物理事件与另一类物理情境相比对，分析两类物理现象依存的条件和遵循的规律，比对两类物理现象的相似性，通过直观性的判断，从熟悉的物理模型中寻找相似的物理模型，这是基于物理现象的相似性实施的模型建构.

典例3 （2020年普通高等学校招生全国统一考试Ⅰ卷理科综合能力测试）

21.如图4，U形光滑金属框abcd置于水平绝缘平台上，ab和dc边平行，和bc边垂直.ab、dc足够长，整个金属框电阻可忽略.一根具有一定电阻的导体棒MN置于金属框上，用水平恒力F向右拉动金属框，运动过程中，装置始终处于竖直向下的匀强磁场中，MN与金属框保持良好接触，且与bc边保持平行.经过一段时间后（   ）.

A.金属框的速度大小趋于恒定值

B.金属框的加速度大小趋于恒定值

C.导体棒所受安培力的大小趋于恒定值

D.导体棒到金属框bc边的距离趋于恒定值

模型建构能力的表现

（1）逻辑推理形成判断，为类比性建构模型提供依据.

①分析物理过程，通过逻辑推理形成F安是等间距滑轨上双棒关联性制约的系统内力，运用电磁感应和力学综合的知识，推断出前棒是电磁阻尼，后面金属棒是电磁驱动，形成双棒关联性制约的物理表象;

②通过逻辑推理形成F安=B2L2（v1-v2）R表达，运用牛顿运动定律判断各自运动状态：

对金属框：F-B2L2（v1-v2）R=m2a2，做加速度减小速度增加的变加速直线运动;

对导体棒：B2L2（v1-v2）R=m1a1，做加速度增加、速度增加的变加速直线运动;

形成如下层阶的认识：

层阶1.导体框和后面金属棒存在相对速度是闭合回路存在感应电流的前提;

层阶2.闭合回路存在电流是导体棒加速和金属框加速度改变的原因;

层阶3.初始速度不同，加速度不同使得金属框架和金属棒存在变化的相对速度;

层阶4.金属框因相对速度增大而使得加速度减小，金属棒却因相对速度的增加而加速度增加，单位时间内金属框速度增量减小，金属棒单位时间速度增加，呈现Δv1<Δv2;

层阶5.趋向稳态的判断，当Δv1=Δv2时，即a1=a2时，相对速度v相=v1-v2恒定，闭合回路产生稳定的电流I=BL（v1-v2）R，金属框和金属棒以相同的加速度保持恒定的相对速度做匀变速直线运动，形成如图5的v-t图像表征;

（2）类比推理建构模型

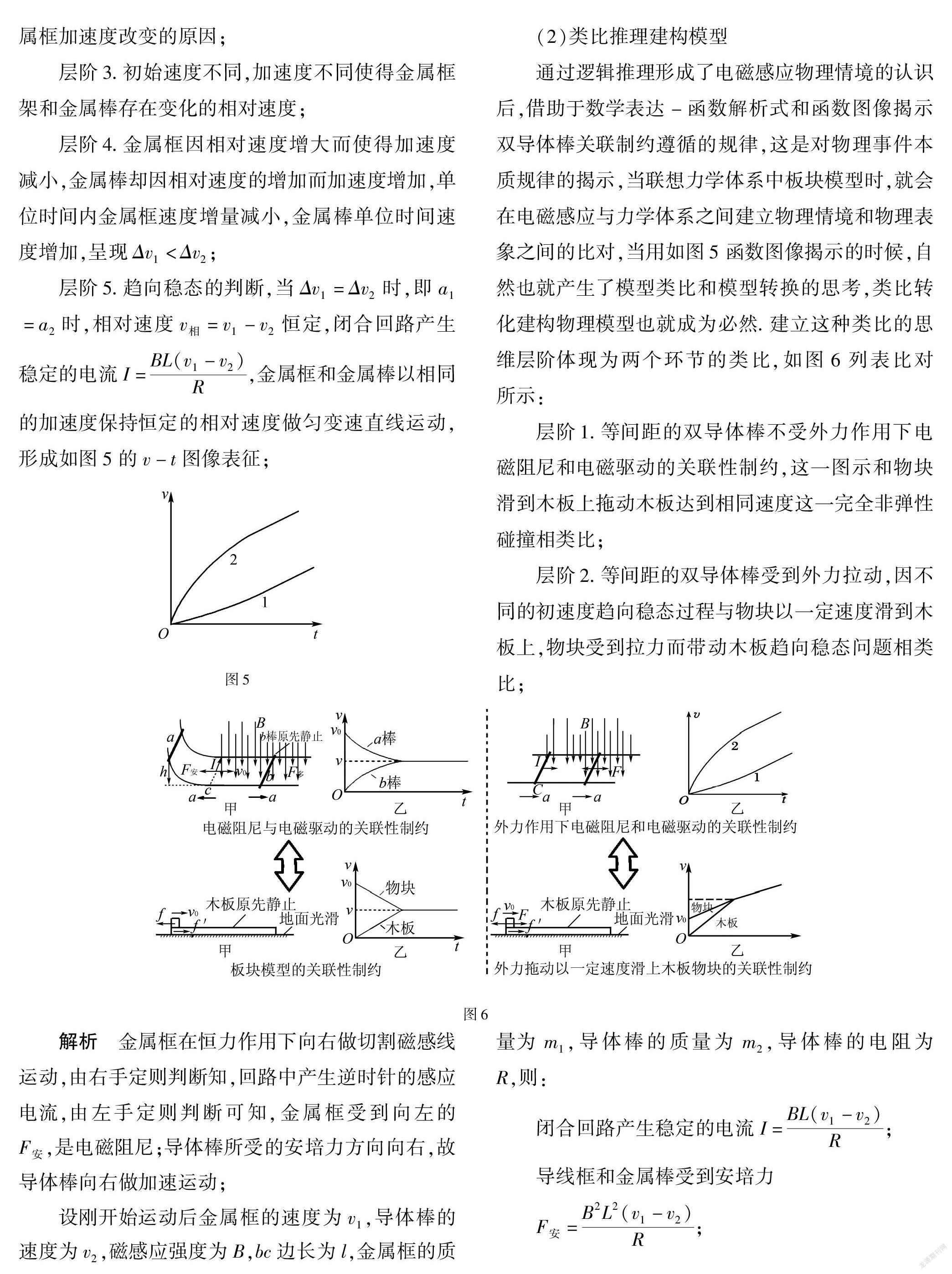
通过逻辑推理形成了电磁感应物理情境的认识后，借助于数学表达-函数解析式和函数图像揭示双导体棒关联制约遵循的规律，这是对物理事件本质规律的揭示，当联想力学体系中板块模型时，就会在电磁感应与力学体系之间建立物理情境和物理表象之间的比对，当用如图5函数图像揭示的时候，自然也就产生了模型类比和模型转换的思考，类比转化建构物理模型也就成为必然.建立这种类比的思维层阶体现为两个环节的类比，如图

6列表比对所示：

层阶1.等间距的双导体棒不受外力作用下电磁阻尼和电磁驱动的关联性制约，这一图示和物块滑到木板上拖动木板达到相同速度这一完全非弹性碰撞相类比;

层阶2.等间距的双导体棒受到外力拉动，因不同的初速度趋向稳态过程与物块以一定速度滑到木板上，物块受到拉力而带动木板趋向稳态问题相类比;

解析 金属框在恒力作用下向右做切割磁感线运动，由右手定则判断知，回路中产生逆时针的感应电流，由左手定则判断可知，金属框受到向左的F安，是电磁阻尼;导体棒所受的安培力方向向右，故导体棒向右做加速运动;

设刚开始运动后金属框的速度为v1，导体棒的速度为v2，磁感应强度为B，bc边长为l，金属框的质量为m1，导体棒的质量为m2，导体棒的电阻为R，则：

闭合回路产生稳定的电流I=BL（v1-v2）R;

导线框和金属棒受到安培力

F安=B2L2（v1-v2）R;

对金属框：F-B2L2（v1-v2）R=m2a2，做加速度减小速度增加的变加速直线运动;

对导体棒：B2L2（v1-v2）R=m1a1，做加速度增加、速度增加的变加速直线运动;

当a1=a2时，速度之差v相=v1-v2保持恒定，系统相互作用的内力F安=B2L2（v1-v2）R为定值，最终金属框和导体棒以恒定的加速度a=Fm1+m2做匀加速直线运动.

A.由于金属框最终做匀加速直线运动，故金属框的速度将一直增加， A错误;

B.由上述分析可知，金属框最终做匀加速直线运动，加速度恒定，B正确;

C.最终闭合回路的电流保持不变，导体棒所受的安培力最终为定值，C正确;

D.金属框与导体棒的速度差Δv保持不变，导体棒离bc边将越来越远，D错误;

故选BC.

层阶四、分析与推理，比较与综合，类比建构物理模型

2021年全国乙卷试题第21题充分体现了高层阶模型建构能力的命题思想.该试题源于单金属棒在电磁阻尼作用下趋向稳态问题分析，但却通过系统内力作用使两金属棒各在不同的空间内追击“相遇”.

典例4 （2021年高考全国乙卷物理试卷）

25.如图7，一倾角为α的光滑固定斜面的顶端放有质量M=0.06kg的U型导体框，导体框的电阻忽略不计;一电阻R=3Ω的金属棒CD的两端置于导体框上，与导体框构成矩形回路CDEF;EF与斜面底边平行，长度L=0.6m.初始时CD与EF相距s0=0.4m，金属棒与导体框同时由静止开始下滑，金属棒下滑距离s1=316m后进入一方向垂直于斜面的匀强磁场区域，磁场边界（图中虚线）与斜面底边平行;金属棒在磁场中做匀速运动，直至离开磁场区域.当金属棒离开磁场的瞬间，导体框的EF边正好进入磁场，并在匀速运动一段距离后开始加速.已知金属棒与导体框之间始终接触良好，磁场的磁感应强度大小B=1T，重力加速度大小取g=10m/s2，sinα=0.6.求： 图7

（1）金属棒在磁场中运动时所受安培力的大小;

（2）金屬棒的质量以及金属棒与导体框之间的动摩擦因数;

（3）导体框匀速运动的距离.

模型建构能力层阶分析

命题意向的显性表现是综合运用牛顿运动定律和功能思维解决电磁感应中单棒趋向稳态过程问题分析.从科学素养目标角度是对科学思维中模型建构、分析与综合和推理与论证的综合考察.其中模型建构能力水平体现为如下层阶：

层阶1.能在熟悉的问题情境中应用常见的物理模型解决问题，属于“识别-应用”.

从知识运用水平上是运用牛顿运动定律解决“已知受力求运动”，从能力层阶上是能科学地运用整体法与部分法描征导体框和金属棒一起在单一重力场中以a=gsinθ做初速度为零的匀加速直线运动，再运用v2t-v20=2ax求解金属棒到达磁场边界的速度.或者利用动能定理W合=ΔEK，即（M+m）gsinθ·s1=12（M+m）v2-0，解得v=2gS1sinθ=1.5m/s;

层阶2.通过分析与推理，识别U形导体框沿斜面做匀加速直线运动追击位于磁场中匀速运动平动切割磁感线金属棒，建构匀加速直线运动追击前方匀速直线运动，两者间距不断减小的物理情境.通过类比“追击相遇”问题情境，建构电磁感应中“追击相遇”的过程模型.分析与推理，通过类比建构模型，这是低转换性的体现;

从知识运用水平上，综合运用电磁感应定律、闭合电路的欧姆定律与力和运动的关系.推理论证形成类比表象的逻辑如下：

（1）求解导体框完全通过磁场区域的时间t=xv;

（2）分析与推理形成U形导体框在t=xv内因加速而推动金属棒运动，能从力和运动的角度揭示导体框和金属棒各自的受力特征，形成各自运动特征的描述和相对位置变化规律的认识，是类别建构模型的关键.金属棒和导体框受力如图8（a）和

图8（b）所示：图8

对导体框：Mgsinα-μmgcosα=Ma框1，做匀加速直线运动;

对导体棒：μmgcosα+mgsinα=B2L2vR，做匀速直线运动;

在t=xv内导体框和金属棒的相对距离Δx1=（v0t+12at2）-x+s0，导体框与前方金属棒的间距不断缩小.这一层阶是综合运用知识，通过科学推理形成物理表象认识，通过与经典力学模型类比，实现将实际问题中的对象和过程转换成后方匀加速直线运动追击前方匀速直线运动过程模型，属于低转换性，为模型建构水平的第四层次水平.

层阶3.分析与综合，逻辑与推理，建构匀速直线运动的导体框推动前方匀加速直线运动的金属棒的物理图景.导线框进入磁场后推理与论证形成模型建构的环节如下：

（1）呈现导体框和金属棒的初始运动状态，推断导线框推动导体棒运动.

其逻辑是导线框因前一过程的加速运动速度大于金属棒，在v棒<v框状态下，导体框受到电磁阻尼和金属棒对它的滑动摩擦阻力而做匀速直线运动，形成“快的匀速追击前方慢的匀加速”的物理图景;

（2）突显v棒=v框临界条件，推断v棒>v框下金属棒拖动导线框加速运动，形成v棒<v框和v棒>v框两类物理情境的图示，从而合理建构“快的匀加速带动后方慢的匀加速”运动的图景，基于这种模型类比建立的新的模型，形成追击问题的图示.

Ⅰ.v棒<v框，棒受到框的推动以a棒2做匀加速直线运动，棒和框受力如图8（c）和8（d）所示：

金属棒：mgsinα+μmgcosα=ma棒2;

金属框：Mgsinα=BI′L+μmgcosα;

Ⅱ.v棒>v框，棒拖动导线框加速运动，加速度分别是a棒3和a框3，如图8（e）和图8（f）所示;图8

金属棒：mgsinα-μmgcosα=ma棒3;

金属框：Mgsinα+μmgcosα-F′安=Ma框3;

解析 （1）根据题意可得金属棒和导体框在没有进入磁场时一起做匀加速直线运动，由动能定理可得

M+mgs1sinα=12M+mv20，

代入数据解得v0=32m/s

金属棒在磁场中切割磁场产生感应电动势，由法拉第电磁感应定律可得E=BLv0

由闭合回路的欧姆定律可得I=ER

则导体棒刚进入磁场时受到的安培力为F安=BIL=0.18N

（2）金属棒进入磁场以后因为瞬间受到安培力的作用，根据楞次定律可知金属棒的安培力沿斜面向上，之后金属棒相对导体框向上运动，因此金属棒受到导体框给的沿斜面向下的滑动摩擦力，因匀速运动，可有

mgsinα+μmgcosα=F安

此时导体框向下做匀加速运动，根据牛顿第二定律可得

Mgsinα-μmgcosα=Ma

设磁场区域的宽度为x，则金属棒在磁场中运动的时间为

t=xv0

则此时导体框的速度为v1=v0+at

则导体框的位移

x1=v0t+12at2

因此导体框和金屬棒的相对位移为

Δx=x1-x=12at2

当金属棒离开磁场时金属框的上端EF刚好进入线框，则有位移关系s0-Δx=x

金属框进入磁场时匀速运动，此时的电动势为E1=BLv1，I1=BLv1R

导体框受到向上的安培力和滑动摩擦力，因此可得Mgsinα=μmgcosα+BI1L

联立以上可得

x=0.3m，a=5m/s2，m=0.02kg，μ=38

（3）金属棒出磁场以后，速度小于导体框的速度，因此受到向下的摩擦力，做加速运动，则有mgsinα+μmgcosα=ma1

金属棒向下加速，导体框匀速，当共速时导体框不再匀速，则有v0+a1t1=v1

导体框匀速运动的距离为x2=v1t1，代入数据解得x2=2.59m=518m

分解复杂的物理问题，运用分析与综合、推理与论证形成对物理过程的认识，从熟悉的物理模型中选择适合的模型来解答，从逻辑推理的自洽性上判断选用模型的合理性，通过认知行为修订和完善心智模型，最终形成适合问题求解的概念模型，是一种主动的内在的心智行为能力，这种科学思维与科学探究并重的模型建构属于较高层阶的水平.

参考文献：

[1] 中华人民共和国教育部.普通高中物理课程标准（2017年版）[M].北京：人民教育出版社，2018.

[2] 廖伯琴.普通高中物理课程标准（2017年版）解读[M].北京：高等教育出版社，2018.

[3] 巍欣，高杰.高考考生科学思维关键要素水平诊断与分析[J].考试研究，2020（01）：29-36.

[4] 曹宝龙.物理模型的建构与教学建议[J].物理教学探讨，2016，35（05）：1-5.

[5] ColleenMegowan-Romanowicz，许桂清.物理建模教学模式简介[J].物理教师，2011，32（08）：1-3.

[责任编辑：李 璟]