从“任意角”的教学设计解读数学教学情境的基本要求
2022-03-27陈小红
陈小红
[摘 要] 以“任意角”的教学设计为例谈数学教学情境的基本要求,即数学教学情境要:真实可信,简明易懂,目的明确,反映本质,系统连贯.
[关键词] 任意角;数学情境;教学设计
数学教学情境越来越被广大数学教师所重视,但在实际教学中往往会出现一系列的问题:如情境的可信度低,为了达到教学目的而人为编造一些假情境;情境纷繁复杂,难以读懂;情境目的性和指向性不明,让学生无法回答;情境过分地掩盖数学对象的本质,不能凸显数学对象的重要特征;情境系统性不够,教学主线不明,层次性不明显等. 笔者以“任意角”的教学设计为例谈谈对数学教学情境的一些基本要求的认识.
教学设计
1. 问题情境
現实世界中的许多运动、变化都有着循环往复的现象,如地球自转和公转带来的昼夜交替和四季变化、月亮的盈亏圆缺以及潮汐涨落,又如车轮旋转、单摆运动、电流变化等. 面对生活中存在着的众多周而复始现象,可以用怎样的数学模型刻画这种变化规律呢?
师:这就是本章要学习的三角函数模型.研究三角函数也是使用研究函数的一般“套路”,会经历怎样的研究过程?
预设:(引导学生回答)研究函数一般经历研究函数的三要素(尤其是定义域与对应法则)、函数的性质、函数的图像、函数的应用等几个重要的过程.
师:本章前2节内容分别为任意角、弧度制,任意角的出现使角的范围不受限制,弧度制的出现让角的表示实数化,这为研究三角函数的定义域提供了知识保障.
设计意图:开门见山,让学生了解本章的概貌,进一步明确学习三角函数的基本步骤,明确学习本章前两节内容的目的.
问题1 初中我们学习过角的概念,初中阶段是如何定义角的?初中阶段学习了哪些角?
预设:平面内,从一个端点引出两条射线组成的图形称为角.初中阶段学习了直角、平角、周角、锐角及钝角.
设计意图:复习初中的角的概念,为后面引发认知冲突打下基础.
问题2 (借助于动画描述)旋转也可以产生角,如何用运动的观念来定义角?
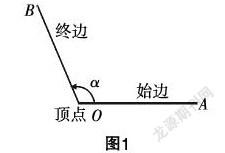
预设:一个角可以看作平面内一条射线绕着它的端点从一个位置旋转到另一个位置所形成的图形. 射线的端点称为角的顶点,射线旋转的开始位置和终止位置分别称为角的始边和终边(因为概念本身的需要,所以将原先的角的两边做了区分,即分为始边与终边).
设计意图:引入旋转意义下的角的概念.
问题3的情境
将汽车的方向盘按逆时针或者顺时针旋转到底,称为方向盘“打死”.驾校师傅常说:方向盘从正位向左(逆时针旋转,下同)打一圈半可以把方向盘向左“打死”,从正位向右(顺时针,下同)打一圈半可以把方向盘向右“打死”.
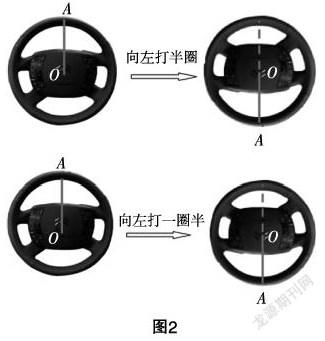
问题3.1 如图2,方向盘从正位向左打半圈,方向盘的某个半径OA逆时针旋转了多少度?方向盘从正位向左打一圈半,方向盘某个半径OA逆时针旋转了多少度?两次独立操作之后,OA的位置一样吗?
设计意图:提出这个问题有3个意图. 意图1,说明角的范围需要从“量”上进行扩充.旋转意义下的角的大小不能由角的始边和终边决定,要看旋转量,即初中学习的角的概念不能解决这些问题,需要“改进”. 意图2,第2小问的结果540°源于学生的直觉结果,即先逆时针旋360°,再逆时针旋转180°,两者“相加”所得. 此时并没有定义超过360°的角,学生的直觉结果为角的加法的概念提供重要的感性素材. 意图3,为轴线角的概念提供实例,也为终边相同的角提供实例.
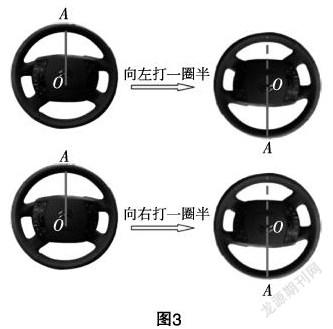
问题3.2 如图3,方向盘从正位向左打一圈半,和从正位向右打一圈半,方向盘某个半径OA旋转的角一样吗?如果不一样,如何区别它们?
设计意图:提出这个问题有2个意图. 意图1,说明旋转意义下的角的大小不能由角的始边和终边决定,不仅要看旋转的量,还要看旋转的方向.旋转方向不同,角是有差别的. 因此,角的概念要区分旋转方向的差异. 这也说明初中学习的角的概念需要进一步“改进”. 意图2同问题3.1的意图3.
2. 学生活动
(1)举一些类似的例子说明角的推广的必要性,如“时钟的秒针2分钟转过多少角度?”“将螺丝钉旋松和旋紧,螺丝刀转过多少角度?”等等.
设计意图:通过举例进一步感受角的推广的必要性.
(2)讨论如何通过建立角的“新”定义解决这些问题.
设计意图:主要讨论如何区分角的旋转方向.
3. 数学建构
在以前的数学学习中,如何来表示具有相反意义的量?如“从某一点向南5米,记为5,则从这一点向北5米记为什么?”
设计意图:利用实数的正负表示具有相反意义的量作为先行组织者,引导学生能产生正向迁移,得出正角、负角的概念.
(1)角的符号——正角、负角
按逆时针方向旋转所成的角叫作正角,按顺时针方向旋转所成的角叫作负角.如果射线没有作任何旋转,也把它看成一个角,叫作零角.
问题4:(操作1)将汽车方向盘从正位先向左旋转一圈半,再回一圈,如何表示某个半径OA旋转的两个角?方向盘某个半径OA经过两次旋转后得到怎样的角?
设计意图:结合前面的问题3.1的第2小问中540°的来源,感受角的加法实质上是两次连续(即第二个角的始边与第一个角的终边重合)旋转的“合效果”,并在此基础上归纳出两角的和的定义.
(2)两角的和的定义
对于两个任意角α,β,将α的终边旋转角β(当β为正角时,按逆时针方向旋转;当β为负角时,按顺时针方向旋转;当β为零角时,不旋转),这时终边所对应的角称为α与β的和,记为α+β. 很容易验证,两角的和的运算满足交换律与结合律.
根据定义,操作1的两次旋转后,相应的角可以记为540°+(-360°).
(3)两角的差的定义
将射线绕其端点分别按逆时针方向、顺时针方向旋转相同的量所成的两个角称为相反角,并规定α的相反角为 -α. 明显α+(-α)=(-α)+α=0°. 把满足x+β=α的角x称为α与β的差,记为α-β. 注意到[α+(-β)]+β=α,因此α-β=α+(-β).
问题5:(操作1)将汽车方向盘从正位先向左打一圈半,再回一圈.
(操作2)将汽车方向盘从正位向左打半圈.
两种操作后的汽车行驶转向效果一样吗?
预设:操作1的两次旋转后汽车的转向的“合效果”等同于操作2旋转后汽车的转向效果,为此我们认为等式540°+(-360°)=180°是合理的.
根据运算规则,也有540°+(-360°)=540°-360°=180°. 說明前面的角的加法和减法及其运算法则是合理的,因为它们保证了运算的结果与实际的结果的吻合性.
设计意图:通过具体的操作,进一步确认两角的和与差的定义是合理的.
(4)坐标系中的象限角与轴线角
操作题:(1)分别作出下列角:-60°,-135°,225°;(2)用量角器作出65°角.
问题6:从前面的操作题中,尤其是用量角器度量角,你能得到怎样的启示?
设计意图:让学生理解,一个角大小的给定,既不取决于终边的位置,也不取决于始边的位置,而是两者相对的位置关系.用量角器度量角,需要将量角器中的“始边”与待度量的角的始边重合. 因此,让各角的始边重合,更方便研究(例如比较两个锐角或钝角的大小等).
为了便于研究,常以角的顶点为坐标原点,角的始边为x轴正半轴,建立平面直角坐标系. 这样,角的终边(除端点外)在第几象限,就说这个角是第几象限角. 角的终边在坐标轴上,就叫这个角为轴线角.
4. 数学应用
例1 在平面直角坐标系内作出60°,420°,-300°角的终边,思考它们之间有什么关系?你能得到更一般的结论吗?(联系前面方向盘向左打半圈与打一圈半的例子)
一般地,与角α的终边相同的角的集合为{ββ=k·360°+α,k∈Z}.
设计意图:引导学生通过归纳得出相应的结论.第一,明确每加(减)360°对应于将终边按逆(顺)时针再旋转一周,因此k·360°+α(k∈Z)与α的终边始终相同. 第二,只有将α的终边按照逆时针或顺时针方向再旋转360°的整数倍后的角才可能与α的终边重合,因此与α的终边相同的角为k·360°+α(k∈Z).
例2 在0°到360°的范围内,找出与下列各角终边相同的角,并分别判断它们是第几象限角:(1)650°;(2)-150°;(3)-990°15′.
设计意图:进一步巩固终边相同的角的关系,明确这样做的目的更容易判断角所在的象限,为后面研究终边相同的三角函数(即第一组诱导公式)提供必要的知识储备.
例3 已知角α与240°的终边相同,判断是第几象限角.
设计意图:进一步巩固终边相同的角的关系,能利用分类讨论思想判断角所在的象限.
5. 课堂小结
(1)知识结构.
(2)思想方法
转化与化归思想,分类讨论思想.
对数学教学情境的基本要求的思考
在高中数学教学中,为了激发学生有意义的学习,教学情境中的问题更应该符合这几个基本要求:真实可信,简明易懂,目的明确,反映本质,系统连贯.
真实可信,即构成问题情境的各个要素的来源要科学而真实,这也是数学教师科学严谨治学的体现. 真实可信是数学教学情境的基本属性. 笔者认为不应为了达到某种教学目的而人为地编造虚无的情境.真实的情境来源有哪些?笔者简单地举几种来源,但不拘泥于这几种来源:第一,从具体的生活实物中选取,例如本案例中“车的方向盘”就是生活实物,这样的情境比较契合任意角的相关概念;第二,从数学或其他学科(例如向量与物理等)的真实的感性材料中选取,从中概括、归纳某些数学概念、规律或公式等;第三,从能让学生产生认知冲突的材料中选取,例如将学生对同一问题的不同解答得到的不同结果作为问题情境,等等.
简明易懂,即一方面问题情境要简明,没有干扰条件,信息要精炼不能冗长;另一方面,问题情境要易懂,表述上要准确而不含糊,无矛盾且有条理,语言具有启发性. 从知识的联系和发展中提出问题,提出的问题贴合教学且自然.例如,本案例中,学生对“汽车的方向盘”比较了解,理解没有困难,而且相关问题的表述比较清楚,没有干扰条件.
目的明确,即问题情境要紧紧围绕当前的教学任务,使得学生的注意力集中在教学任务上. 例如,本案例中问题情境的目的很明确,让学生从“汽车方向盘从正位向左打一圈半”“角的终边相同但旋转量不同”中感受到初中学习的角的“不够用”,因此角在“量”上的扩充成为自然的需求;再如,“汽车方向盘从正位向左打一圈半,与向右打一圈半”会产生截然不同的结果,让学生感受到旋转的方向也是初中学习的角所无法解释的,因此角的符号的引入也成为自然的需求.
反映本质,即“问题要问在点子上”,情境中的问题直接能反映所学新知识的本质,引导学生思维指向教学任务,而不能干扰学生思路. 例如,本案例中,“方向盘向左打一圈半”是逆时针旋转了多少度,学生回答是540°,这种直觉实际是两角的“和”的一种心理意向,即两角和的本质就是“连续旋转”的一种刻画,在这里可提出“540°是360°与180°的和”的初步结论;待后面有了正角和负角概念后,再次提出问题“将汽车方向盘从正位先向左打一圈半,再回一圈,方向盘某个半径OA经过两次旋转后得到怎样的角”,即可明确一个角再加一个负角对应于怎样的“连续旋转”,为进一步完善两角和的概念做铺垫.
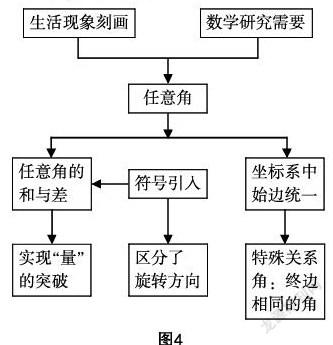
系统连贯,即问题应按照数学知识的发生发展过程,以相应的数学思想方法为主线,组成一个循序渐进、具有内在联系的问题体系,这些问题都要为持续不断地揭示新知识的本质服务,为学生循序渐进地掌握新知识引路. 本案例中按问题呈现顺序,对应的基本目的依次是:介绍本章的概貌与研究方法—介绍前2小节的内容与目标—回顾旧知(初中所学的角的概念)—形成新知(旋转意义下角的定义)—形成认知冲突(旧知无法解决的新问题)—完善新知(利用角的符号刻画旋转方向,利用角的运算扩充角的范围). 其中形成认知冲突与完善新知是关键的两步,利于学生深刻理解角的扩充的必要性与合理性.问题情境的系统连贯性也为学生用图表来厘清各知识点的逻辑联系,进一步形成知识网络结构带来了极大的方便.例如,本案例的总结用“学生先总结,教师再梳理”的方式,以图表的形式呈现.对图表做如下解读:角的扩充的源头有两个,一个是现实的需要,另一个是数学的本质;有几个问题用初中的角的概念不能解决,如角的旋转方向、角的旋转量等,由此引发的认知冲突都是产生新的角的概念的动力;如何解决这些问题——用符号区分角的旋转方向,用角的和与差来突破角的范围的桎梏;符号的引入进一步扩充了参与运算的角的范围;在坐标系中将角的始边置于同一位置,更方便研究角;研究终边重合的角的终极目的是研究三角函数的周期性等.
