基于Lasso回归和ARIMA模型的城市生活垃圾产生量预测
——以宝鸡市为例
2022-03-26俱国鹏惠姣姣
房 妮, 俱国鹏, 惠姣姣, 雷 霁
(1.宝鸡文理学院陕西省灾害监测与机理模拟重点实验室,陕西 宝鸡 721016;2.宝鸡文理学院数学与信息科学学院,陕西 宝鸡 721016)
近年来,我国经济高速发展,城市化进程加快,但同时,城市生活垃圾产生量也迅速增长.国家统计局数据显示,2019年我国城市生活垃圾清运量已达24 206.2万t,约为1999年城市生活垃圾清运量的2.11倍[1-2].大量生活垃圾的产生不仅造成了“垃圾围城”和环境污染,也给城市卫生管理工作带来了严峻的挑战.精确的城市垃圾产生量预测是研究城市垃圾管理和资源化利用方案的前提.近些年,我国学者将数理统计模型引入垃圾产生量预测中,开展了一系列理论与实践研究:有学者采用灰色理论GM(1,1)模型对建筑垃圾[3]和餐厨垃圾[4]进行了预测,但灰色模型只适用于限制条件少、通用性强的情况,不能模拟未来社会经济、人口和政策突变情况下生活垃圾的产生情况,计算也相对复杂[5];也有学者运用ARIMA(p,d,q)模型预测了垃圾产量发展趋势[6],但ARIMA(p,d,q)模型只考虑了时间因素对垃圾产生量的影响,不能反映垃圾产生量的诸多影响因素之间的内在联系;还有较多学者采用多元线性回归法进行垃圾产量预测[7-10],但常由于影响因素之间的多重共线性问题而导致模型精度不高或由于对影响因素的定量化分析不够精确而影响了预测结果的准确性.
基于以上原因,本研究提出采用一种处理具有多重共线性数据的高级算法——Lasso回归来进行城市生活垃圾产生量的预测.通过在回归模型中增加惩罚项,Lasso回归可将过小的回归系数压缩到0进而剔除,以此实现自变量的自动筛选,从而在保证模型稳定性的同时实现模型的精简.另外,在应用研究中可直接使用R 语言软件进行Lasso回归建模,大大减少了计算量,提升了计算速度.目前,经济学、医学等领域已有不少研究者成功采用Lasso 方法进行预测[11-13],但在国内外城市垃圾产生量预测中,未见其应用.本研究以宝鸡市生活垃圾产生量为研究对象,分析Lasso 回归对于城市生活垃圾产生量预测的可行性,探索预测的新方法.考虑到垃圾产生量的影响因素中,社会经济、消费及基础设施建设等因素均符合时间序列模型的要求,因而进一步采用时间序列ARIMA模型对城市生活垃圾产生量的主要影响因素分别进行预测,在得到各影响因素的预测值后再利用Lasso模型对宝鸡市城市生活垃圾产生量进行预测.
1 材料与方法
1.1 研究数据来源
由于生活垃圾产生量难以统计,故以生活垃圾清运量代替生活垃圾产生量作为因变量(Y),在城市生活垃圾产生量的四大类影响因素——人口、经济发展水平、居民生活水平及基础设施建设水平中,选取统计数据连续、详实的8个常见因素作为自变量(X1~8)进行宝鸡市生活垃圾产量的预测建模.所用数据来源于《宝鸡市统计年鉴》(2009—2019).变量的具体解释见表1.

表1 2009—2019年宝鸡市生活垃圾产生量及影响因素统计Tab.1 The basic data of MSW production and its influencing factors in Baoji from 2009 to 2019
1.2 研究方法
首先,利用条件指数法(κ值)和方差膨胀因子(VIF)对数据进行影响因素共线性判断;其次,利用Lasso回归模型筛选出主要影响因素,构建生活垃圾产量预测模型,并进行精度检验,然后引入ARIMA(p,d,q)模型,对各主要因素2020—2025年的数据进行预测;最后,应用Lasso回归模型,对宝鸡市2020—2025年生活垃圾产量进行预测.
1.2.1 影响因子共线性判断 在多元回归中,较多的自变量之间容易出现多重共线性问题.多重共线性是指线性回归模型中的自变量之间由于存在精确相关关系或高度相关关系,而使模型估计失真或者难以估计准确[14].用来进行共线性诊断的方法有特征值法、条件指数法(κ值)、方差比例法、方差膨胀因子法(VIF)以及逐步回归法等.本文利用κ值和VIF 值进行多重共线性检验,明确各影响因素的相关性.一般认为,当VIF>10或κ>100 时,存在严重的多重共线性[15].
1.2.2 Lasso回归模型
1)方法原理.Lasso回归是一种压缩估计,通过构造一个惩罚函数得到较为精炼的模型,压缩一些回归系数,具有子集收缩的优点,是一种处理具有多重共线性数据的有偏估计[16].

式中:α为截距项;βj为第j个变量对应的系数.
在Lasso回归中,通常采用Cp值最小原则来筛选自变量.Cp统计量是选择最优子集的一种方法,Cp值越小表示所选子集个数最优,具体定义为:

式中:p为参与回归的自变量个数;n表示样本的数量;SSEp表示p对因变量进行回归后的残差平方和;δ2表示所有自变量对因变量进行回归时,方差均值的预测[16].
通过Cp值最小原则,将回归系数非常接近于0 的变量剔除,即可获得最优子集,同时得到最佳的回归方程.
2)模型性能评估.采用平均绝对百分比误差(MAPE)、均方根误差(RMSE)和决定系数(R2)3个指标对Lasso模型的预测效果进行评估.计算公式为:
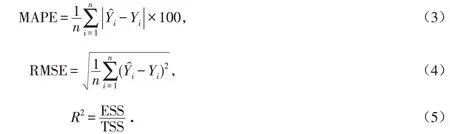
式中:Yi表示生活垃圾产生量的原始值;Ŷi表示生活垃圾产生量拟合值;n=11;ESS 表示回归平方和;TSS 表示总离差平方和.RMSE 和MAPE 越接近于0,预测精度越高;决定系数(R2)又称拟合优度,其值越接近于1,说明拟和程度越好.
1.2.3 ARIMA(p,d,q)模型
1)ARIMA(p,d,q)模型(自回归差分滑动平均模型).该模型是一种常用的时间序列预测分析方法,可认为是AR(p)(自回归)模型与MA(q)(滑动平均)模型的差分组合[17].ARIMA(p,d,q)的模型表达式如下:
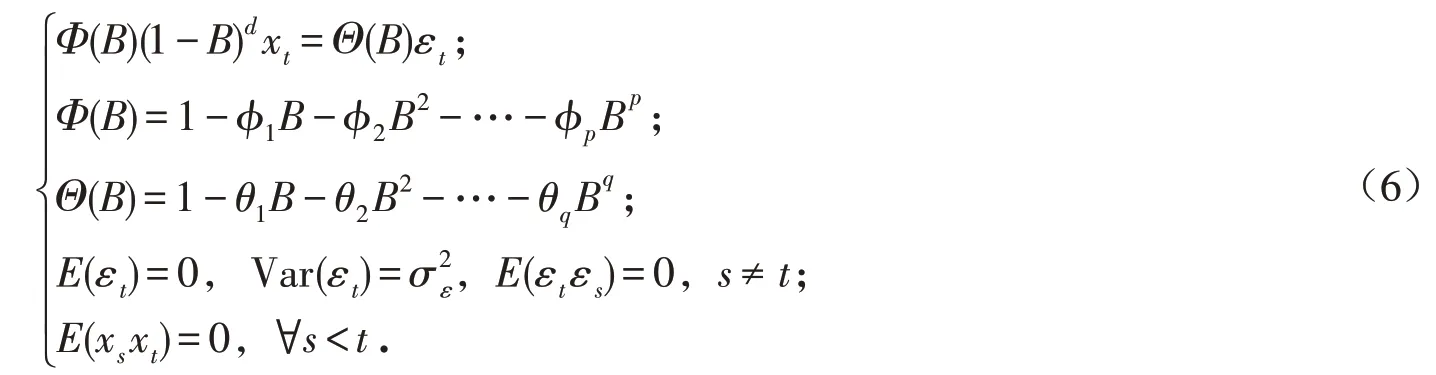
式中:B为延迟算子;Bnxt=xt-n;Φ(B)表示自回归延迟算子;Θ(B)表示移动平均延迟算子;p为自回归阶数;d为差分次数;q为移动平均阶数;xt表示当前t时刻的值,且xt由过去的p个历史值xt-1,xt-2,…,xt-p加权组成,ϕ1,ϕ2,…,ϕp表示其权重;εt,εt-1,εt-2,…,εt-q表示高斯白噪声,θ1,θ2,…,θq表示其权重[18].研究中各影响因素的ARIMA(p,d,q)模型预测过程如图1所示.

图1 ARIMA(p,d,q)模型预测流程图Fig.1 The prediction flow chart of ARIMA(p,d,q)model
2)ARIMA(p,d,q)的建模步骤如下:
数据平稳性检验:根据时间序列的自相关系数图来判断时间序列是否平稳.如果序列被验证为不平稳,则需要通过差分变换或者对数差分变换使其满足平稳性条件;如果d阶差分后序列满足平稳条件,则可确定d.
模型定阶:根据自相关图(ACF)和偏自相关图(PACF)来确定自相关阶数p和移动平均阶数q,确定模型ARIMA(p,d,q).
参数估计与诊断:对ARIMA(p,d,q)模型进行参数估计,并判断其残差序列是否为白噪声序列,若残差序列为白噪声序列,则通过检验[18];若拟合的模型无法通过检验,则重新确定参数p和q,重新选择模型进行拟合.
最后,利用ARIMA(p,d,q)模型进行预测.
1.2.4 统计学方法 研究中Lasso 模型以及ARIMA(p,d,q)模型的构建、数据分析均使用R 语言中的lars 包实现.
2 结果与讨论
2.1 共线性判断
利用κ值和VIF值对各自变量进行多重共线性检验,结果如表2.

表2 多重共线性判断Tab.2 Multi-collinearity judgment
表2显示,κ值远大于100,各变量的VIF值均超过10.无论κ值还是VIF值都说明8个自变量之间存在明显的多重共线性.因此,若利用普通线性回归模型分析8个自变量和因变量之间的关系,并采用最小二乘法求解线性回归系数,则各系数必然会出现较大偏差,且无法得到各系数的无偏估计.因此,采用Lasso回归将冗余预测变量的回归系数压缩到0,进而获得更简洁的模型,同时可处理共线性问题,防止过度拟合,提高预测精度[14].
2.2 Lasso回归模型构建
根据Cp值最小的原则,使用Lasso回归模型,从8个影响因素中筛选了6个具有非0系数的影响因素,分别为:人均生产总值(X2)、社会消费品零售总额(X3)、常住人口数(X5)、道路清扫面积(X6)、机械清扫面积(X7)和市容环卫专用车辆(X8),所对应的非0系数分别为0.000 4、0.023 2、-6.458 8、0.033 4、-0.094 3、0.471 7,故得到生活垃圾年产生量的Lasso预测模型为:
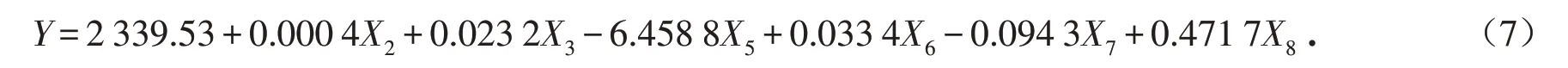
式中所有变量解释同表1.
2.3 Lasso回归模型检验
经计算,模型(7)的RMSE 为0.014 9,MAPE 为0.798 2%,均接近于0;拟合优度R2为0.998,接近于1.这些指标都证明了模型(7)可达到高精准度的预测效果,可以用来预测未来几年生活垃圾的产生量.另外,将Lasso回归模型得到的生活垃圾产生量预测值与实际值进行对比,预测值与实际值贴合程度较高,整体趋势基本相同,再次证明了模型的有效性(图2).
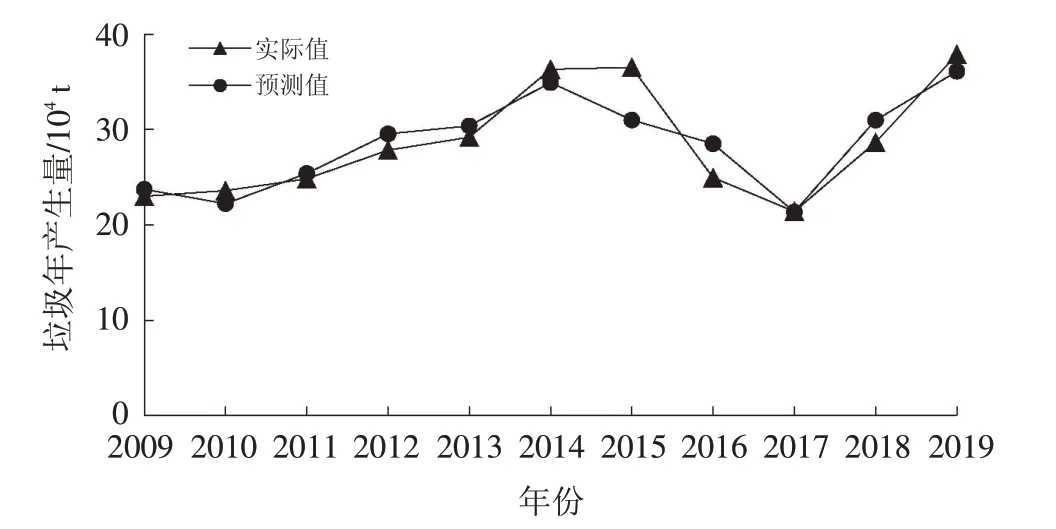
图2 生活垃圾产生量Lasso回归预测值与实际值对比Fig.2 Comparison of Lasso regression predicted value and actual value of MSW production
2.4 影响因素的预测
对Lasso回归筛选出的6个影响因素均采用图2所示的ARIMA(p,d,q)进行预测,选定的模型参数和残差序列的检验结果如表3,得到的6个影响因素的预测数据如表4.通过检验,p值均小于0.05,即残差序列均为白噪声序列,由此说明研究中关于6个影响因素建立的ARIMA(p,d,q)模型是合理的.因此,可以在这6个影响因素(自变量)预测数据的基础上继续进行Lasso回归,从而进行生活垃圾产生量(因变量)的预测.

表3 影响因素的ARIMA(p,d,q)预测模型Tab.3 ARIMA(p,d,q)prediction model of influence factors

表4 宝鸡城市生活垃圾产生量影响因素预测Tab.4 Prediction of influencing factors of MSW production in Baoji
2.5 Lasso回归预测结果与分析
结合表4 各影响因素的预测数据,根据回归模型(7),得到宝鸡2020—2025 年的城市生活垃圾年产生量和人均垃圾日产生量预测值(表5).

表5 2020—2025年宝鸡城市垃圾产生量预测值Tab.5 Prediction value of MSW production in Baoji from 2020 to 2025
对比我国西北地区两个省会城市西安和西宁,宝鸡城市生活垃圾年产生量和人均日产生量均较低,但其生活垃圾产生量年增长率却较高.西宁2020—2035 年的城市垃圾平均年增长率仅为3.71%[7],西安2020 年城市垃圾产生量增长率为6%[9],而宝鸡2020—2025年城市垃圾平均年增长率高达15%.由此可见,“十四五”期间宝鸡市将面临严峻的由生活垃圾产量持续增加所带来的城市卫生管理压力.宝鸡市应全面推进生活垃圾源头分类,同时应确保垃圾收集、收运、处理、处置的其他环节全程分类,不断提升资源化利用水平,尽早探索“无废城市”的建设之路.
3 结论
1)通过Lasso回归对自变量间存在多重共线性进行处理,将自变量地区生产总值和城市居民人均可支配收入剔除在模型外,对城市生活垃圾产生量建立了Lasso回归模型.通过检验该模型拟合度R2为0.998,模型的RMSE 为0.014 9,MAPE 为0.798 2%,说明Lasso 回归预测精度高,在城市生活垃圾产生量预测方面具有推广价值.
2)通过时间序列ARIMA(p,d,q)模型,对人均生产总值、社会消费品零售总额、常住人口数、道路清扫面积、机械清扫面积和市容环卫专用车辆6个自变量进行了预测.在此基础上,通过Lasso回归模型预测了宝鸡市生活垃圾产生量.预测得出,2020—2025年宝鸡城市生活垃圾产生量将分别达到25.76×104、38.44×104、35.89×104、41.59×104、48.39×104、52.71×104t,生活垃圾产生量平均年增长率为15%,增速过快.因此,宝鸡市应尽快完善生活垃圾投放、收集、运输和处理的全程分类系统,不断提升监管能力,强化分类处理与资源化利用水平,通过资源的最大化利用实现垃圾减量.
