基于密度峰值法的复杂网络聚类增长维度研究

许 英，罗梦迪

(新疆财经大学 统计与数据科学学院，乌鲁木齐 830012)

复杂网络作为复杂系统的结构化表示，因其与万维网、交通、生物和社会系统等许多实际系统之间存在的相关性，受到了许多研究领域学者的关注。大量的真实网络表现出来的鲜明特征都明显有别于随机网络和规则网络，这种特征被称为小世界或无标度性。在开创性工作中，Song等人[1]发现各种真实复杂网络在所有长度标度下具有分形和自相似特性，其中盒覆盖法被用于计算复杂网络的分形维数。Shanker等人利用聚类增长方法研究了复杂网络的分形问题[2-3]。随后，分形问题在网络科学中也得到了广泛的研究[4-10]，复杂网络分形研究的几何法最主要的工作之一就是计算网络的分形维度，而网络的分形维度的计算问题最终可归结为在给定盒子尺度下，计算能够覆盖网络所需的最小盒子数量的问题。两种独立的方法：盒覆盖方法[11-18]和聚类增长方法[19-20]被广泛用于计算复杂网络的分形维度。近年来，大量的研究对这两种方法进行了扩展，并且对复杂网络的多重分形特征进行了分析。

本文主要专注于聚类增长方法的研究。聚类增长方法的思想是随机选择种子，并计算以种子为中心，半径为r的超球体内的节点数M(r).为改善统计量，将所有节点依次设置为种子重复计算，最终得到在相同半径r内的平均节点数M(r).复杂网络维数的估计值是通过对统计数据的双对数刻度进行线性回归而获得的。Bo等人[21]提出了一种基于紧密度CC的方法来测量复杂网络的分形维度，即选择最重要的节点作为种子。在本文中，主要关注种子在整个网络中心位置的选择，利用密度峰值聚类方法来测量复杂网络的分形维度。基于这种方法，选出中心节点作为种子计算半径为r的超球面内的节点数的平均值M(r).通过与原始方法和基于紧密度CC方法的比较，发现使用基于密度峰值法的方法可以更好地获得复杂网络的分形维度。

1 方法

1.1 局部随机游走距离

给定一个无向无权的网络G=(V，E)，其中V是节点集合，E是边集合。随机游走是一个重要的过程，可以代表随机步行者经过的一系列节点。转移概率矩阵P，Pij=aij/k表示留在节点i的随机步行者在下一步将步行到j的可能性，其中A=(aij)是网络的邻接矩阵，ki表示节点i的度。Liu等人[22]提出了一种基于局部随机游走(LRW)的节点距离度量，其时间复杂度低于其他基于随机游走的距离度量。

给定一个从节点i开始的随机游走者，这个游走者在t步之后到达节点j的概率表示为πij(t).该系统演化方程可表示为πi(t)=PTπi(t-1)，其初始系统状态为πi(0)=ei，第i个位置为1其余位置为0.一个随机游走者经过t步后的访问，LRW指数可以定义如下：

(1)

其中|E|是网络的边数。

叠加的随机游走SRW度量是t步时间内LRW的叠加，它描述了随机游走者是从起始节点的连续释放。该方程式定义为：

(2)

节点i和节点j之间的局部随机游走距离(LRWD)定义如下：

(3)

因此，可以基于以上公式计算网络的距离矩阵D={dij}，显然距离D是对称的。如果随机游走的步数受到限制，距离函数就是一个度量。如果t≤|E|/2，则容易证明dij(t)+djk(t)≥dik(t).在以下实验中，将网络的直径设置为随机游走步长t，通常小于n.

1.2 确定网络的种子

Rodriguez等人[23]提出了一种聚类方法，该思想基于以下观点：聚类中心被具有较低局部密度的邻居包围，并且它们与具有较高局部密度的任何点之间的距离都相对较大，Liu等人[24]推广了该方法以估计复杂网络的中心。

对于每个节点i计算ρi和δi，其中ρi是节点i的局部密度，δi是节点i与较高密度的节点之间的距离，这两个量都取决于节点之间的距离dij.网络的距离矩阵D={dij}可由方程(3)计算，节点i的局部密度ρi可定义为：

(4)

其中dc是一个修正参数，控制权重降解率，由文献[24]，dc的选择对密度峰值聚类法的最后结果不是至关重要的，这里选择dc为dij的平均值。具体来说，ρi表示与节点i的距离接近于dc的节点的数量。

节点i和任何其他具有更高密度节点的最小距离是δi，被定义为：

(5)

注意，聚类的中心被确定为ρi和δi异常大的节点，在此基础上，网络的中心总是出现在决策图的右上角。

但是对聚类中心的选取需要人为干预，其中包含了主观因素，不同的人可能会选择不同的点作为聚类中心，因此，定义一个对ρi和δi综合考虑的量γi：

γi=ρiδi

(6)

显然，γi值越大，越有可能是聚类中心。对γi进行降序排序，非聚类中心的γi的值分布比较平稳，而从非聚类中心过渡到聚类中心时，γi的值会有一个明显的跳跃，此时就能通过数值更加准确的找到聚类中心，避免主观因素所造成的选择误差。

1.3 分形维度的计算

大多数现实世界的网络都具有异构拓扑特征，聚类增长法是一种研究复杂网络分形和自相似特性的成功的分析技术。但是在已有的聚类增长方法中，原始方法没有研究网络边界节点的影响，基于紧密度CC的方法忽略了其他重要节点的影响。从理论上讲，如果一个节点位于复杂网络的外围，则节点的数目M(r)将缓慢增加，然后在r增加到固定点时非常快地增加。因此，M(r)vsr的双对数标度的线性回归可能不遵循幂律，并导致表征复杂网络的分形特性失败。如果选择一个种子且其位置位于整个网络的中心，虽然不会发生上述现象，但是中心的选择可能会存在偏差。基于这种观察，提出了一种基于密度峰值法的经过改进的复杂网络聚类增长维度研究的方法。

基于上述密度峰值聚类法选择种子节点，进行以下步骤，即可得到复杂网络G的分形维度:

步骤1：用式(3)计算复杂网络的距离矩阵，用式(4)-式(6)计算ρi、δi和γi确定中心节点；

步骤2：选择上述中心节点作为种子，令初始半径r1=1，从各个种子开始计算半径为r1=1的超球中的节点数M(r1)；

步骤3：用r2=r1+1，r3=r2+1，…来代替r1重复步骤2，直到所有的节点都被某些半径所覆盖；

步骤4：绘制M(r)和半径r的双对数图，通过拟合直线的斜率得到网络的分形维数。

注意，M(r)被认为是r的函数：

M(r)～rdf，

(7)

其中M(r)是以种子节点为中心，r为半径的超球体内的节点数，df是复杂网络的分形维度。由于分形维度是利用密度峰值聚类法的中心得到的，因此将该方法称为基于密度峰值的方法。也可以使用其他的中心来测量复杂网络的分形维度，例如把所有节点当成种子的方法(原始方法)和基于紧密度CC的方法。下面验证基于密度峰值方法的有效性，并将该方法应用于一些真实世界的复杂网络和NW小世界网络的测量。同时，与原始方法、基于紧密度CC的方法进行了比较。

2 仿真实验

本文采用R软件进行仿真，选取四个典型社交网络进行分析：(1)Karate网络是社会网络分析中广为分析的网络，网络有34个点和78条边，；(2)Dolphins 网络是2003年新西兰附近的62只海豚之间关系网络，共有62个节点和159条边；(3)Yeast网络时酵母菌蛋白质相互作用网络，共有2 361个节点和7 182条边；(4)Netscience网络是网络科学领域科学家合作网络，共有379个点和914条边。

首先，利用密度峰值法确定四个真实世界网络的中心节点作为计算分形维度的种子，如图1所示。

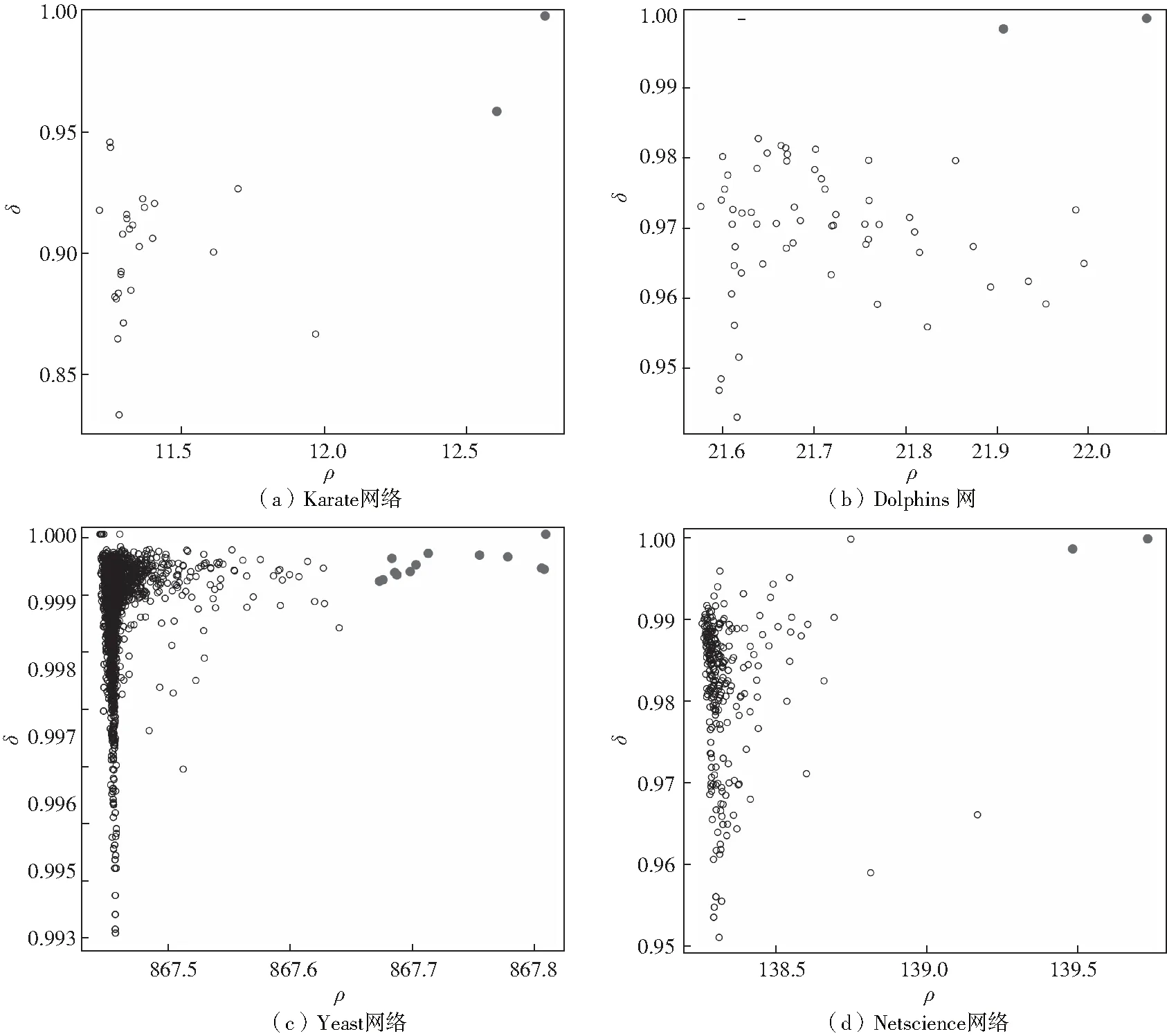
图1 根据密度峰值法确定四个真实世界网络的种子决策

在本节中，首先要证明选择的种子是否在复杂网络的分形特性方面起着重要作用。这里使用上述四个真实社交网络，这些网络的一些基本信息显示在表1中，其中列出了网络的节点数N、边数M和基于密度峰值方法、基于紧密度方法和原始方法获得的分形维度df以及均方误差。

表1 四个真实世界网络基本信息、分形维度和均方误差的比较

图2 通过三种方法获得四个真实世界网络的M(r)与r的对数-对数图

以上结果表明，确定节点的核心位置对于计算复杂网络的维度也至关重要。如果将本文方法的步骤1中所选的中心节点替换为紧密中心性最大的节点或所有节点，即可获得基于紧密度的方法和原始方法。

为了评估本文所提出的方法的性能，分别介绍了该方法、基于紧密度的方法和原始方法在小世界网络分形分析中的性能。小世界网络由N=1 000，2 000，3 000，3 500个节点组成的网格构成，每个节点最初有个2m邻居，对于每一对原来未连接的节点，以概率p添加一条边来连接这两个节点，该小世界网络记为NW(1,N,2m,p)，在这个过程中，重边和自环被排除在外。利用该模型构造了四个不同加边概率p和初始度2m的网络。用本文提出基于密度峰值方法、基于紧密度的方法和原始方法测量网络的分形维度和均方误差如表2所示，从中可以看出，对于几乎所有考虑的NW小世界网络，基于密度峰值方法要优于其他方法，虽然本文的方法对第四个NW网络的均方误差并不比紧密度优，但是均方误差也已经足够小，认为这个结果也是很好的。结果还表明，网络的维度与网络结构密切相关，如网络的连边概率p和初始度2m.

表2 四个小世界网络基本信息、分形维度和均方误差的比较

3 结论

在经典的聚类增长方法中，测量复杂网络的维度时，需要选择所有节点作为种子来减少统计误差。现实世界的网络大多具有异质性的拓扑结构，更倾向于选择网络的外围节点作为种子节点。因此，在这种情况下不可能得到一个合理的结果。当选择网络的多个中心节点作为种子节点时，可以很好地观察到网络的缩放特性。本文考虑了密度峰值法来选择那些γi大的节点作为种子节点。结果表明，该方法在处理复杂网络的分形维度问题时是有效的。需要注意的是，复杂网络的分形只能在一定的尺度范围内观察到，利用本文提出的方法，可以很容易地得到真实网络和NW小世界网络的分形维度。此外结果还表明，在计算复杂网络的分形维度时，每个节点的中心性也很重要。